基于MATLAB多端口网络S参量分析软件设计及应用
钱建波 于正永
(江苏电子信息职业学院现代教育技术中心 江苏淮安 223003)
0 引言
多端口器件在微波集成电路系统中的应用越来越广泛,因此较为快速、便捷、准确地分析多端口器件的特性参量十分必要。传统的处理方法是将多端口器件看作一个多端口网络,提取其散射特性、阻抗矩阵以及导纳矩阵等参量,进而分析器件及系统的特性。任意多端口网络S参数的推导过程通常要求各个互联传输线的宽度(阻抗)相等,但在实际电路系统中常遇到阶梯跳变、直角拐角、T型接头等连接传输线宽度不同的情况,针对这个局限性,本文引入微带线不连续性等效电路模型[1],将上述的阶梯跳变、直角拐角、T型接头等分别作为一个单元子网进行处理,这样可以有效地解决上述局限,并基于MATLAB平台[2]开发了分析软件,结合实例进行验证和分析。
1 软件设计
1.1 总体设计
计算机程序的设计主要分为界面和内核两部分。直接在命令行调用函数进行计算,必须对程序的编写过程非常熟悉,因此,界面程序可以为用户提供良好的操作接口,使计算程序通用化。而内核部分主要包括子网S参量的获取和互联后综合网络S参数的计算。其软件设计总体流程如图1所示。
1.2 单元子网模块设计
本文采用微带线不连续性等效电路模型[1]获取单元子网的端口参量,程序的编制主要分为等效电路基本参数准备和各种不连续性具体算法实现。

图1 软件设计总体流程图
1.2.1 基本参数准备
在计算不连续性等效电路前,需要给出设计参数,并得出相关推导参数。设计参数包括介电常数εr、介质厚度h(不连续部分长为Δz=2h)、工作频率,根据各种不连续性电路的结构给出相应的微带线尺寸。相关的推导参数根据文献[3]中公式由设计参数计算获取,包括分布电容及电感、附加电容、边缘电容和边缘电感等。
1.2.2 各结构具体算法实现
传输线的不连续部分通常出现在两个或更多的等效开路端连接处。在将开路端等效电路应用于阶梯跳变、直角拐角、T型接头时,需要注意互电感及耦合电容的加入和变化。每一个开路端等效电路都是等效电容、电感组成的T形网络,无论不连续性电路的结构如何变化,程序编制的流程是:分别计算每个开路端等效电路——T形网络三支的阻抗,利用变换公式获得该T形网络(二端口)的级联矩阵,再根据开路端等效电路的连接关系求得总级联矩阵,最后由级联与散射矩阵的互换关系得到该单元子网的S参数。此外,传输线虽不需要建立不连续性等效电路模型,但作为组成微波系统的单元子网,其网络参数计算也纳入该模块,可直接由S参数计算公式获得。
1.3 多端口网络互联模块设计
互联模块主要包括子网及互联信息设置、连接散射矩阵算法实现。
1.3.1 子网及互联信息设置
假定应用人员已对整体网络进行了合理划分。一般而言,划分后的子网多为传输线和各种不连续性等效网络。但有时整体网络过于复杂,也可以对其进行粗分,将功能较为完整的一部分划分成子网,该子网内包括多个不连续性及传输线,如分支线耦合器等。在计算整体网络参数前,先运用网络互联模块计算子网参数;在计算整体网络时,将这些复杂子网与各种不连续性网络以同样的方式进行处理。
程序的输入参数包括子网个数、每个子网的端口数、每个子网的S参数、互联端口的对数、互联端口的编号。需要注意的是,每项参数必须一一对应,这要求划分网络时对其进行编号,并对所有端口按网络顺序统一编号。在整个子网信息设置过程中,以这些编号为依据。
1.3.2 连接散射矩阵算法实现
根据连接散射矩阵理论,首先需要构造联合散射矩阵。该矩阵按照非互联端口和互联端口顺序排列,但是在导入子网S参数时,则按照网络顺序导入。若将子网S参数一个个提取并全部重新排列,较为繁琐且容易出错。在研究端口排列顺序的变换规律后发现:列向量a、b中的元素按照同样的规律同时排列以后,只要对S矩阵的行按同样的顺序进行调整,再对列也进行如上的变化即可。如下:
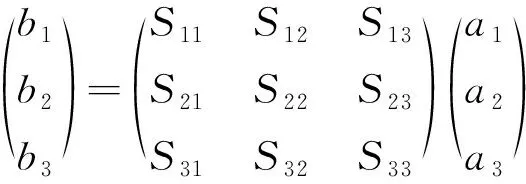
(1)
这样,只需将导入的各子网矩阵按网络编号以对角线方式构造成原始的全矩阵。如下:
(2)
式(2)中,bnetN和anetN分别表示第K个子网的散射波和入射波向量,SN表示第N个子网的散射矩阵。
在输入互联关系以后,按照重排的端口顺序,进行上述变化,便可以得到计算所需的联合散射矩阵式。此后,按非互联和互联端口对联合散射矩阵分块,由理论推导的公式编程计算得到整体网络参数。
2 实例验证及分析
2.1 T型接头
单元子网T型接头结构示意图如图2(a)所示。基本参数为:W1=1.44 mm,W2=W3=0.4 mm,介电常数εr=2.55,介质层高度h=0.5 mm,不连续性传输线长度Δz=2h。本文软件计算结果与IE3D数值软件计算结果对比曲线如图2(b)所示,从图2(b)中可以看出,T型接头S11、S21幅度两种方法吻合良好,平均误差小于2%。

(a) T型接头结构示意图
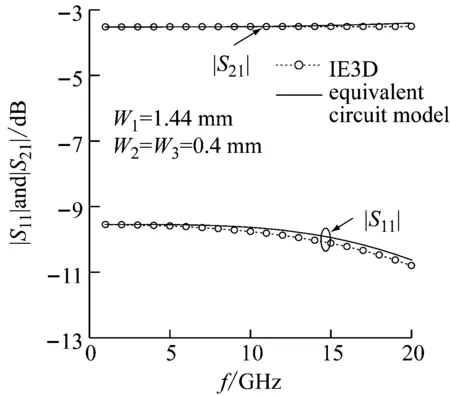
(b) T型接头仿真结果对比曲线
2.2 分支线定向耦合器
分支线定向耦合器结构示意图如图3所示,基本参数为εr=2.55,介质高度h=0.5 mm,Δz=2h=1 mm,W1=1.44 mm,W2=2.4 mm。将其划分成8个子网,标识为20个端口,其中子网1、2、3、4是T型接头,子网5、6、7、8均为传输线,各子网参量都可以通过单元子网软件提取获得,如图4所示。
图5给出了本文软件计算结果与IE3D数值分析软件结果的对比曲线。从图5(a)中可以发现,|S11|、|S41|的软件计算结果与IE3D计算结果趋势一致,在中心频率f=10 GHz附近,软件计算结果更为理想化,这是因为散射矩阵法并不考虑连接过程中的不理想性,其结果是否理想在子网划分及设计时就已经决定,主要受子网参数影响。|S21|、|S31|计算和仿真结果在中心频率处都在-3 dB附近,变化趋势相符。分支耦合器直通口和耦合口的相位在理论上应为90°,软件计算结果和IE3D仿真结果相位变化趋势一致,且在中心频率f=10 GHz附近,S21、S31的相位差都在90°上下波动。计算相位斜率较大,即变化较快,产生偏差的原因也主要是子网相位误差的积累。

图3 分支耦合器结构示意图
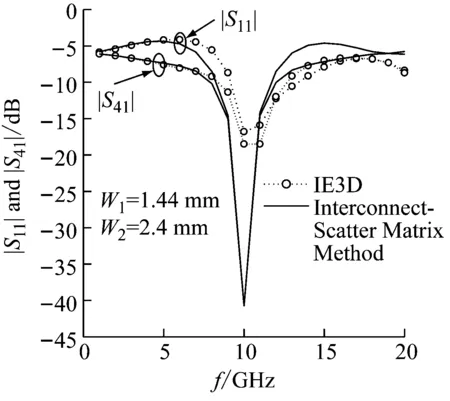
(a) |S11|、 |S41|程序计算及仿真结果

(b) |S21|、 |S31|程序计算及仿真结果
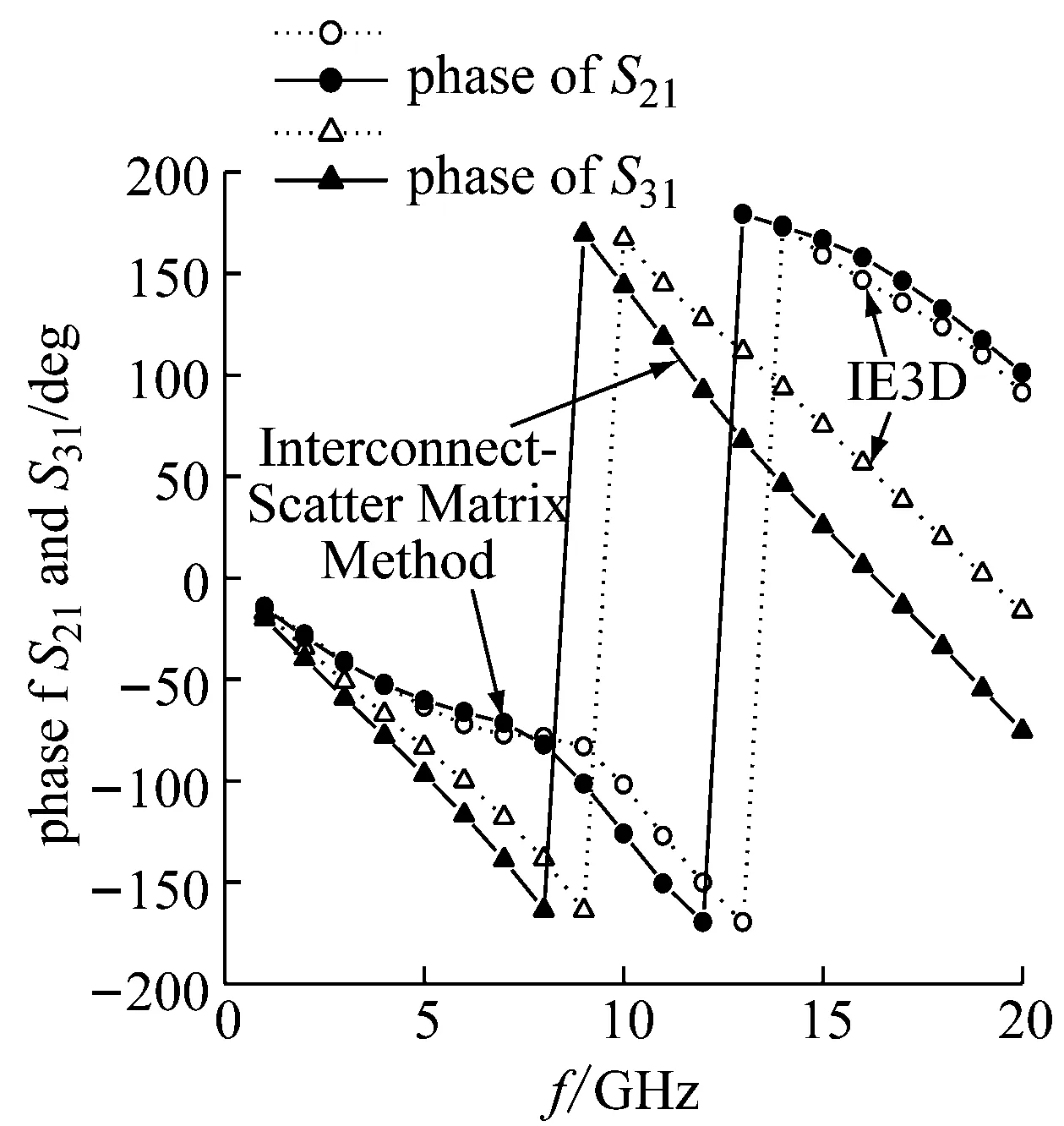
(c) 分支耦合器S21、S31相位的程序计算及仿真结果曲线
3 结束语
本文基于微带线不连续性等效模型及理论,通过将由阻抗不同传输线互联而成的阶梯跳变、直角拐角以及T型接头等视为一个单元子网,从而克服了传统多端口互联网络S参量计算要求满足互联传输线特性阻抗相等的局限性,根据连接散射矩阵基本原理,使用Matlab平台设计了S参量分析软件,通过单元子网T型接头和多端口网络分支线定向耦合器两个实例验证发现,所开发软件的计算结果与IE3D计算结果吻合良好,平均误差小于2%。

