能量收集多跳D2D无线传感网络中的中继选择算法*

叶剑锋，夏林中，管明祥

(深圳信息职业技术学院 信息与通信学院，广东 深圳 518172)

0 引 言

无线传感网络(Wireless Sensor Network,WSN)通过采集数据实现对环境的监测，被广泛应用于农林环境监测、军事情报探测、城市结构安全监测以及卫生医疗等领域。作为一种新兴的WSN网络架构，能量收集多跳D2D无线传感网络[1]融合无线功率传输技术[2]、D2D通信技术[3]和ad hoc网络[4]的优势和特点，能够延长WSN网络使用寿命并保持连接性，同时扩大无线电覆盖范围并提供可靠的通信。相较于传统的WSN，能量收集多跳D2D无线传感网络的出现，大大拓展了WSN的发展与应用。由于有能量发射基站的存在，并且网络中的节点数量较多，如何选择合适的中继节点协助通信，从而提高远距离节点通信的连通性是能量收集多跳D2D无线传感网络领域研究的重点。

能量收集中继节点从接收到的射频信号中收集能量，并利用该收集的能量将信号从一个D2D用户传输到另一个D2D用户。关于能量收集多跳D2D网络中的中继选择的研究，2017年，文献[5]考虑能量收集中继节点，推导了瑞利衰落信道下的中断概率表达式以及高信噪比情况下的渐近中断表达式。能量收集无线协作网络中，2017年，文献[6]提出随机中继选择作为一种协作选择方案将解码的源信号转发到目的地，源节点能够根据信道增益条件选择适当的中继链路。2018年，文献[7]提出随机路径选择(Random Path Selection，RPS)协议，通过该协议可以协作源节点和中继节点之间的数据传输。2020年，文献[8]彻底分析了系统的性能，包括中断概率和瑞利衰落信道上可达到的遍历容量，通过蒙特卡洛模拟结果推导并验证了所考虑系统的中断概率的解析表达式。2021年，文献[9]使用最短路径的方法进行节点的选择，以使能量消耗最小，进而增强网络的存活时间。然而实际通信中，无线功率传输技术的收集效率有限会导致信噪比下降，中断性能需要进一步提高。

人工智能推动了社会和行业的新一轮的发展，“十四五”规划中提出人工智能是引领未来科技发展的重要技术之一。由于人工智能中的聚类算法不需要训练集，是一种无监督算法，算法简单快速。聚类算法被用来在无线传感网领域进行中继选择的研究起步较早。2010年，文献[10]为了大大减少了网络探测的规模，通过人工智能领域中的聚类算法探测获取主干路径信息，提高了中继节点选择的成功率。2011年，文献[11]利用聚类K-means 算法对启发式算法的初始解进行调整优化，实现对节点的分组。2016年，文献[12]仅考虑实际物理位置，对节点坐标进行聚类保证节点的位置上的均匀分布。2017年，文献[13]提出一种基于无监督学习聚类K-means 算法以帮助基站选择中继节点，基站通过该算法可以了解设备本身的分布并自动选择中继节点。2018年，文献[14]提出一种新型聚类的路由协议，通过动态权重的处理进行中继选择进而优化多跳路径。以上研究使用聚类相关算法虽然能够选择出合适的中继，但是研究场景过于理想，是在传感器节点携能可保障通信的条件下进行的,能量不足会引发通信质量下降的问题，场景需要更贴合实际。此外，距离不能反映出全部的信道状态信息，仅用距离作为聚类的特征进行节点的中继选择，算法的实际应用性差。因此，需要研究实际通信中面临的能量无线功率传输技术中的能量收集效率以及实际通信环境对中继节点选择的影响。

为解决现有算法在能量收集多跳D2D无线传感网络中通信中断率较高的问题，本文从能量收集效率和实际的通信状态两方面综合考虑，提出一种改进的K-means聚类算法进行中继选择，以减小能量收集多跳D2D无线传感网络中节点的通信中断率，实现远距离节点的多跳通信。

1 系统模型

在能量收集多跳D2D无线传感网络中，如图1所示，存在一个能量发射基站(Base Station，BS)，由该基站向该辐射区域内的无线传感器节点提供通信能源供应。该能量发射基站用B表示。网络中一共有N+2无线传感器节点，每个节点都配备了一个能量收集器。传感器发射节点用S表示，目的节点用D表示，其余传感器节点(称为空闲节点)用i表示，其中i∈{1,2,…,N}。由于信道衰落，通信距离受限，传感器节点S与节点D进行远距离通信需要连续借助k个空闲节点，形成多跳D2D链路。

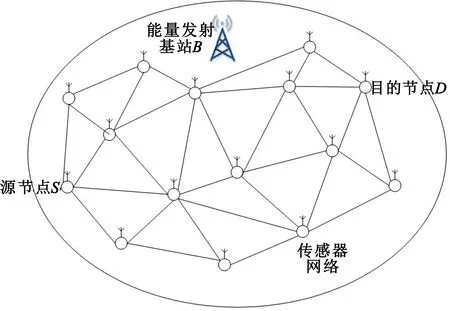
图1 能量收集多跳D2D无线传感网络

所有节点都配备有单个天线，数据传输是通过正交时隙上的时分多址(Time Division Multiple Access，TDMA)实现的。定义从源节点到目的节点的数据传输持续时间是T，那么链路中的两个节点之间的每一跳时隙为τk=T/(k+1),τk的时长由能量采集和数据传输这两个阶段构成。源节点S和空闲节点i使用βτk进行能量采集，然后，在链路中的每一跳使用(1-β)τk进行数据传输，其中β表示能量收集时间因子(0<β<1)[15]。以空闲节点i为例，在每一跳时隙，所收集到的能量存储在电容器中的是

(1)

式中：0≤μ≤1表示能量转换效率，取决于能量收集器的设计；P是能量发射站发射的功率；α是路径损耗指数；gBi是能量发射基站与智能体节点i的信道功率增益；ds,i、di,i+1、di,D、dB,s、dB,i分别表示源节点与空闲节点、空闲节点之间、空闲节点与目的节点、能量发射基站与源节点、能量发射基站与空闲节点的距离。

得到传感器节点i收集到的能量，那么用于通信数据传输的功率为

(2)

信噪比(Signal-to-Noise Ratio，SNR)是衡量通信系统可靠性的指标。SNR越小，表明通信接收方接收到的信息越不准确，当SNR小到一定程度时，接收方则完全不能接收到发送方的信息，造成通信中断。因此，用SNR的大小来评判无线传感器的通信连通性。基于由传感器节点i的能量收集器得到的功率，传感器节点i接收到源节点S信号的接收信噪比为[16]

(3)

同理，能量发射站B向传感器节点i发送功率，传感器节点i接收到的SNR为

(4)

目的节点D接收到智能体节点i的信号，其接收到的SNR为

(5)

传感器节点S与节点D进行远距离通信需要连续借助k个空闲节点，形成多跳D2D链路，这条链路中的中继节点用lj表示，其中j∈{1,2,…,k}。那么，这条链路的通信接收SNR为[16]

γ=min{γSl1,γl1l2,γl2l3,…,γlkD} 。

(6)

2 中继选择算法

根据以上建立的系统和对问题的分析，下面对能量收集多跳D2D无线传感网络的中继选择算法进行描述。文献[14]使用实际物理距离作为聚类特征进行处理，距离这一物理量不能充分表征通信环境，该算法缺少实际应用价值。为了使信道环境对节点的影响描述更符合实际，从而减小源节点到目的节点的通信中断率，本文提出一种基于信噪比因子的聚类特征，如式(7)所示：

(7)

该因子能同时反映节点i与源节点S、目的节点D和能量发射基站B的经过通信信道的SNR之间的关系。其中，分子项表示节点i接收到的SNR乘积，分母项表示节点i发送的SNR。由接收和发射的比值作为聚类的特征，相较于距离这一物理量更能反映出信道对节点的影响。

将该因子依据最小欧氏距离原则进行计算，第m+1次迭代下的聚类中心是

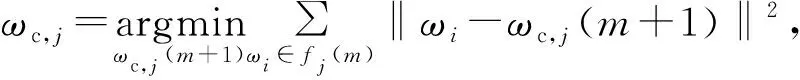
(8)

因为聚类中心的位置和网络中节点的实际存在位置不一定吻合，我们提出选取与聚类中心的欧氏距离差值最小的ωi因子对应的节点作为中继节点，如式(9)所示：

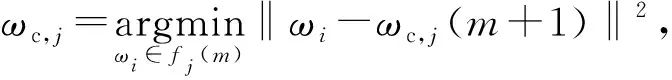
(9)

然后由公式(10)按照与目的节点的实际物理距离，从远到近的顺序进行重排列，即得到最终的中继选择路径：

path=sort(ωc,1,ωc,2,…,ωc,k) 。

(10)

由此根据实际的通信信道环境，选择得到最终的k个中继节点lj,j∈{1,2,…,k}。

算法流程如图2所示。

图2 改进K-means聚类的中继选择算法流程图

算法具体步骤如下：

Step1 输入距离、信道增益等数据，计算得到的信噪比因子作为样本集。

Step2 初始化任选k个聚类中心，ωc,1(0)，ωc,2(0)，…,ωc,k(0)。

Step3 将样本集的样本按最小欧氏距离原则分配给k个聚类中心，在第m次迭代中，若对于i有‖ωi-ωc,j(m)‖<‖ωi-ωc,s(m)‖,j,s=1,2,…,k,j≠s，则i是属于第j个聚类域，即i∈fj(m)。

Step4 如果ωc,j(m+1)=ωc,j(m)，根据公式(9)、(10)计算得到k个中继节点lj,j∈{1,2,…,k}，算法迭代结束；否则，返回到Step 2，进行下一次迭代。

Step5 输出最终的中继节点。

3 仿真实验与结果分析

3.1 仿真设置

本节进行仿真实验以验证所提算法的性能。仿真参数设置如表1所示。信道为瑞利信道，信道功率增益gi,i+1是一个指数分布的随机变量，概率密度函数为fgi,i+1(t)=λexp(-λt)，取λ=1。进行1×104次独立重复仿真实验以验证算法的性能。

表1 仿真实验参量设置

3.2 能量收集时间因子对算法的影响

从图3中可以看出，在0.05≤β≤0.4范围内，能量收集时间因子β越大，链路的信噪比越大，表明在分配的时隙内增加一定的能量收集时间，会提高通信链路的信噪比。因为收集到的能量增多，用于通信的功率会变大，根据信噪比公式可知，增大功率会提高链路的信噪比。另外，能量发射器的发射功率越大，链路的信噪比也越大，提高能量发射器的发射功率，也会提高中继链路的信噪比。

图3 能量收集时间因子β与平均信噪比的关系

3.3 能量收集时间因子β与中断率的关系

从图4中可以看出，在0.05≤β≤0.4范围内，链路的中断率随着β的增大而减小。其原因是节点通信进行能量收集的时间越长，其功率也越大，信噪比也越大，因而中断率减小，与图中的功率与中断率表现出来的关系吻合。

图4 能量收集时间因子β与中断率的关系

3.4 不同中继选择方法的性能对比

不失一般性，根据前面的分析，选取β=0.2，实验次数1×104。

3.4.1 中继路径的信噪比

从图5中能够看出，所提的改进算法的信噪比最大，在相同条件下，比最短路径算法平均大3.12 dB。该结果表明，有了能量发射站的存在，并且考虑实际条件下的通信信道情况，所提改进算法的中继性能优于其他传统算法。另外，这四种方法中，直传(无中继)方式的信噪比最小。该结果表明，使用中继节点进行协助通信可以提高无线传感网络中远距离节点通信链路的联通性。

3.4.2 链路的通信中断率

从图6中可以看出，所提的改进算法得到的通信链路的中断率最小，相同条件下，比最短路径算法中断率平均减小了6.80%，相比于其他算法，所提的改进算法的通信连通性最好，可以提高能量收集多跳D2D网络中中继节点的中继性能。

3.4.3 不同范围的中断率

图7中曲线表明，所提的改进算法得到的通信链路的中断率最小；随着分布范围的增大，所有中继选择算法得到的链路的中断率都会增加。因为信道存在衰落，衰落会随着距离的增大而增大，导致信噪比减小。因此，在节点数量不变的情况下，范围越大，节点之间的平均距离则越大，中继选择算法得到的链路随着距离的增大，其中断率则越大。

图7 算法在不同分布范围的算法的中断率对比曲线

3.5 节点数量对中继选择算法的影响

由图8可知，所提的改进算法得到的通信链路的中断率最小。算法的中断率随着网络中空闲节点数量的增加而减小，因为在分布范围保持不变的情况下，节点数量增加，那么任意两点之间的距离将会减小，由此在瑞利信道下两节点之间的信噪比相对会增大。

图8 算法在不同节点数量下的中断率对比

3.6 本文算法和最短路径算法的时间复杂度

经计算，本文所提算法的时间复杂度是O(mNk)，其中，m是算法的迭代次数，N是节点个数，k是聚类中心数，m和k是常数，时间复杂度与N成线性关系，可简化为O(N)。最短路径算法的时间复杂度是O(VE)，其中，V是连接图中顶点的个数即节点的个数N，E是边的个数。当E为常数时，时间复杂度可简化为O(V)。由此，本文所提的改进算法的时间复杂度和最短路径算法的时间复杂度相当。

4 结束语

在能量收集多跳D2D无线传感网络中，为了减小源节点到目的节点通信的中断概率，本文提出了基于改进聚类的中继选择算法。信噪比因子作为聚类特征，并且根据距离重排序，能够智能地选择出符合实际通信环境下的中继节点。与其他方法的对比仿真实验结果表明，在1×104独立重复实验中，综合考虑能量无线功率传输技术中的能量收集效率以及实际通信环境对中继节点选择的影响，所提改进算法在信噪比和中断率方面性能突出，优于现有的最短路径算法、随机选择算法和直传策略。

在未来研究中，为了提高模型的泛化性，将考虑考虑非线性能量收集模型。同时，为了提高最优中继个数的快速设置，将研究自适应聚类算法在该模型中的应用。