组合跳变随机平移宽间隔混沌跳频序列设计*

黄 琪，杨宇晓，江陈卓

(南京航空航天大学 航天学院，南京 211106)

0 引 言

随着电子对抗技术的迅速发展，安全通信已成为飞行器通信系统的重要发展方向。射频隐身技术通过对信号特征参数的优化设计，提高主动辐射源信号的抗干扰/抗截获能力。通信系统是飞行器搭载的主要辐射源之一，射频隐身通信系统具有重要的研究意义和应用价值。最大信号不确定设计是射频隐身通信系统的重要实现途径，通过通信参数的不规则跳变设计，使对抗方难以预估，从而实现抗干扰/抗截获通信。

通信信号频域特征的不确定设计[1]研究较早，主要集中在跳频序列的随机性设计方面，已有较多的研究成果。跳频序列宽间隔设计[2]是跳频通信的重要内容。通过跳频频点的宽间隔处理，跳频通信系统可以更有效地对抗窄带干扰、宽带阻塞式干扰、跟踪干扰及多径衰落等[3-4]。

国内外学者提出的经典的宽间隔设计方法包括：陈文德提出的去中间频带法[5]，通过丢弃频率集中间的部分频点实现宽间隔跳频，存在频点浪费的问题；冯建利[6]对随机平移替代法(Random-Shift-Replace method,RSR)[7]提出改进，基于m序列构造的跳频序列获得了较好的周期性、汉明相关性和更大的跳频间隔、频隙数，存在降低序列平衡性的问题；牛强军[8]改进了对偶频带法(Dual-Band method,DB)[9]，简化了宽间隔跳频序列生成结构，提高了汉明相关性，但存在频率间隔受限的问题。

综上所述，在跳频通信中，跳频序列有着至关重要的作用，将跳频序列进行宽间隔处理，可以进一步提高跳频系统的抗干扰性能，因此宽间隔跳频序列在跳频通信中已得到广泛应用。然而，随着研究工作的深入，仍存在一些待解决的挑战：一是传统随机平移替代法基于“窄点”修正的思想构造宽间隔跳频序列，存在破坏跳频序列的平衡性的问题，需要针对此问题提出改进方法；二是由于构造宽间隔跳频序列的控制参数较多，参数选取不当会导致多个序列性能难以兼顾的现象，需要对序列控制参数进行寻优设计。

为解决上述问题，本文基于混沌跳频序列，首先提出一种组合跳变随机平移的宽间隔设计方法(Combined-Hopping-Random-Shift method，CHRS)。该方法将两个混沌跳频序列进行组合跳变，利用得到的组合跳变序列对目标混沌跳频序列进行宽间隔映射，实现了混沌跳频序列的宽间隔处理。然后，利用跳频序列的宽间隔特性、平衡性、汉明自相关性等序列特性的数学表征，构建基于CHRS宽间隔设计方法的复合目标优化函数，以序列长度和频隙数为优化对象，引入粒子群算法实现了宽间隔混沌跳频序列的控制参数寻优，完成了宽间隔混沌跳频序列固有特性的均衡设计，实现了宽间隔混沌跳频序列的综合性能最优化。

1 宽间隔混沌跳频序列

宽间隔混沌跳频序列通过对传统混沌跳频序列进行宽间隔处理，使跳频序列的相邻频隙大于固定阈值，以提高跳频通信系统的抗干扰性能。

1.1 混沌跳频序列

混沌跳频序列是常见的跳频序列类型，混沌跳频序列经由混沌系统映射产生的混沌时间序列量化得到。目前产生混沌时间序列的混沌映射包括Tent映射、Logistic映射、改进型Logistic映射等。混沌跳频序列的生成框图如图1所示。

图1 混沌跳频序列产生原理图

本文采用改进型Logistic混沌映射方法，利用混沌系统对初值的敏感依赖性可以产生数量众多的信号，其定义如式(1)所示：

(1)

本文采用余弦映射法实现混沌时间序列{xi}的量化。该方法比较容易，计算量小，其定义如式(2)所示：

Xi=floor(arccos(xi)·q/π),xi∈(-1,1) 。

(2)

式中:q为频隙数。

1.2 宽间隔跳频序列

宽间隔跳频序列定义如下：

对于任意频点xi∈X(X为跳频序列)，d0为最小跳频间隔，满足

|xi+1-xi|>d0，

(3)

那么，X为宽间隔跳频序列。

如果

|xi+1-xi|≤d0，

(4)

那么，X不满足宽间隔跳频序列要求，xi+1为跳频序列的“窄点”。

相较传统跳频序列，宽间隔跳频序列的优越性主要体现在：分散了干扰信号的出现时间，避免了通信系统丢失连续频隙内信息的风险，进一步提高了通信系统的抗干扰能力；增加了干扰方对跳频信号的搜索时间，增强了通信系统的抗跟踪能力；跳频频率间隔大于信道的相关带宽，利于实现频率分集，提高了通信系统的抗多径衰落能力。

2 粒子群算法

粒子群算法(Particle Swarm Optimization,PSO)通过模拟鸟群的捕食行为来解决优化问题。该算法首先在可行解空间初始化一群粒子，通过不断迭代来找到最优解。每一次迭代，粒子通过个体极值pBest和全局最优极值gBest来更新自己，然后搜索当前空间解中的最优粒子。

在搜索最优粒子的过程中，粒子根据式(5)更新自己的速度：

Vi=wVi+c1r1(pBest[i]-Xi)+c2r2(gBest-Xi)。

(5)

根据式(6)更新自己的位置：

Xi=Xi+Vi。

(6)

式中：w为惯性权重；Vi为第i个粒子的速度，Xi为第i个粒子的位置；c1和c2为非负常数，称为加速度因子；r1和r2是分布于区间[0,1]的随机数。

粒子群算法充分利用自身经验和群体经验来调整自身的状态，可以有效地对系统的参数进行寻优，优化目标。粒子群算法与本文所要解决问题相匹配，因此本文选择粒子群算法来实现寻优设计。

3 组合跳变随机平移法

3.1 CHRS宽间隔设计方法

本文以RSR宽间隔设计方法为基础，引入组合跳变序列，提出CHRS宽间隔设计方法。RSR宽间隔设计方法定义如下：

设跳频序列X={x1,x2,…,xN}，xi∈X，d为最小跳频间隔，将xi+1(i>0)与xi比较，并作如下变换：

(7)

式中：ui一般取(xi+1mod (q-2d-1))，q为频隙数。

RSR宽间隔设计方法对混沌跳频序列中的“窄点”进行平移使序列满足宽间隔，降低了原序列的平衡性，因此，CHRS宽间隔设计方法取消“窄点”判断与平移，本质从部分频点修正变为全部频点统一宽间隔映射，提高了序列的平衡性；CHRS宽间隔设计方法利用两个混沌跳频序列组合形成跳变序列，控制频点映射，相比单个跳频序列，提高了序列的复杂度。

本文在RSR宽间隔设计方法的基础上，对目标混沌跳频序列{xi}取模运算得到选择序列{wi}，如式(8)所示：

wi=ximod 2,i=1,2,…,N。

(8)

利用{wi}在两个辅助混沌跳频序列{yi}、{zi}间进行跳变选择，得到组合跳变序列{tempi}，如式(9)所示：

(9)

利用{tempi}对目标混沌跳频序列{xi}的频点依次进行宽间隔映射，如式(10)所示：

(10)

根据式(10)得到的{xi}为宽间隔混沌跳频序列。

基于混沌跳频序列，CHRS宽间隔设计方法与RSR宽间隔设计方法的对比框图如图2所示。

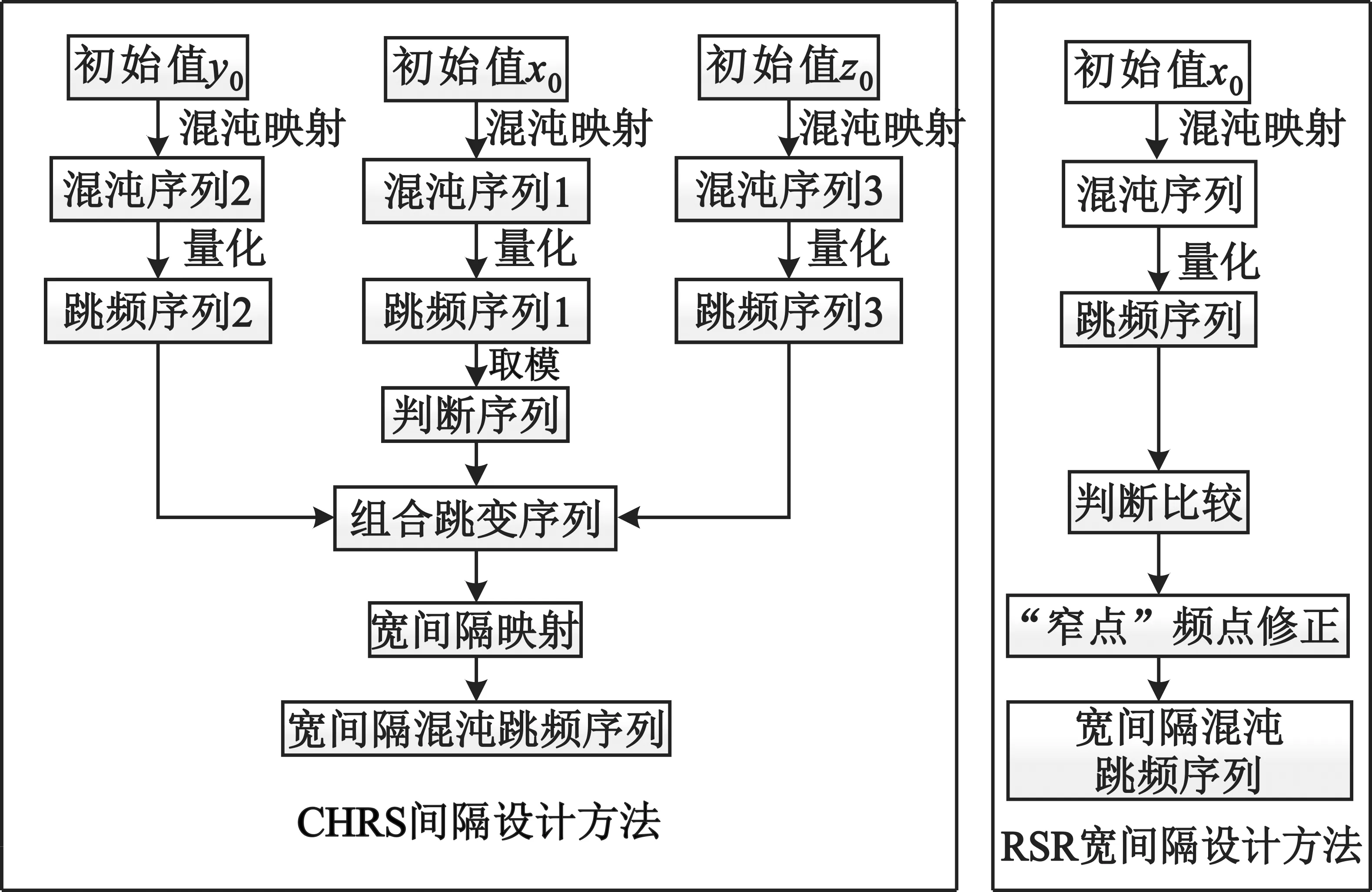
图2 CHRS宽间隔设计方法与RSR宽间隔设计方法对比框图

CHRS宽间隔设计方法流程图如图3所示。

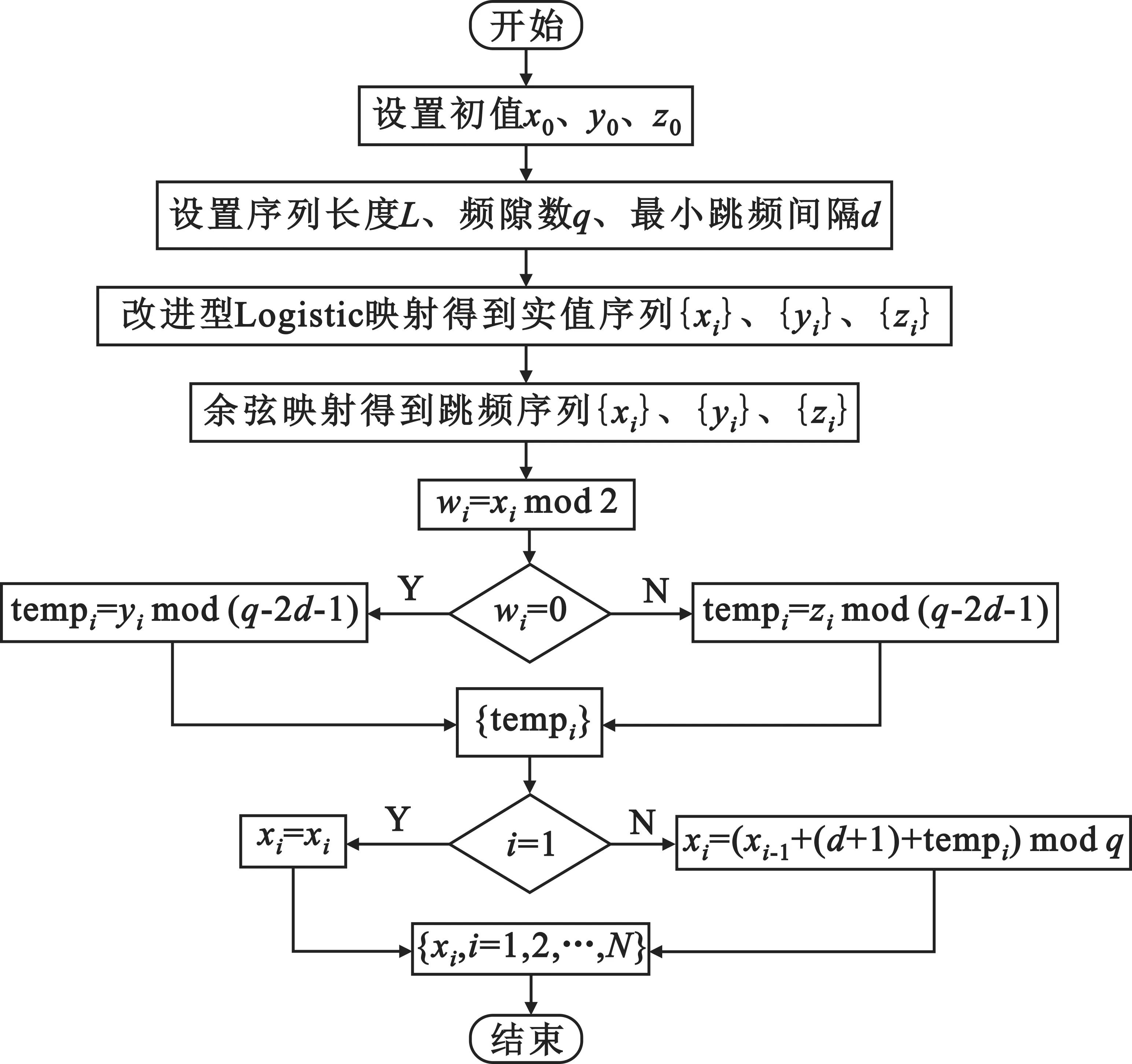
图3 CHRS宽间隔设计方法流程图

3.2 CHRS宽间隔设计方法的性能评估指标

(1)平衡性

平衡性表征序列的频隙分布特征。平衡性越好，平衡性参数δ越小，则跳频序列的抗干扰能力越好，跳频通信系统的载波越不易泄露。平衡性参数定义如下：

(11)

式中：gi为第i个频隙fi在序列中出现的次数，L为序列长度，q为频隙数。

(2)汉明相关性

汉明相关性[10-11]表征序列间的碰撞特性。汉明相关性越好，汉明相关性参数Ramax/R(0)、Rcmax/R(0)越小，则跳频序列的抗多径干扰和多址组网能力越好，跳频通信系统内部干扰越少。

跳频序列的汉明自相关性表示序列自身在任意时延下频点重合的可能性，汉明互相关性表示两个序列在任意时延下频点重合的可能性，分别用归一化汉明自相关参数、归一化汉明互相关参数来表征。

归一化汉明自相关参数的定义如下：

设序列长度为L的跳频序列X={x(0),x(1),x(2),…,x(L-1)},Y={y(0),y(1),y(2),…,y(L-1)}，则

(12)

归一化汉明互相关参数的定义如下：

(13)

式中：

(14)

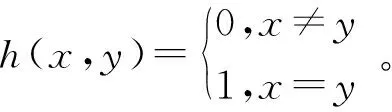
(15)

(3)复杂度

近似熵[12]表征混沌系统输出序列产生新模式的概率大小。近似熵越大，序列的复杂度越高，随机性越强。近似熵定义如下：

ApEn(m,r,N)=Φm,N(r)-Φm+1,N(r) 。

(16)

式中：m为维数，s为相似容限，L为序列长度。

(4)初值敏感性

混沌系统的初值敏感性可实现跳频通信系统的码分多址功能。初值敏感性表示为初值存在微小差别时，混沌系统产生的两个序列之间的差值。

(5)序列个数

跳频序列集中的序列个数应尽可能多，以实现多址通信。

(6)宽间隔特性

跳频间隔宽有利于跳频通信系统获得优良的抗跟踪干扰能力。跳频序列中的任意相邻频点之间的差值即为跳频间隔，平均跳频间隔的定义如下：

(17)

综上所述，理想的宽间隔跳频序列应该具有优良的平衡性、汉明相关性、复杂度、初值敏感性，满足宽间隔要求，序列数目尽量多，因此，本文将以上指标作为评价标准，验证组合跳变随机平移法的优越性。

4 基于粒子群算法的序列构造参数寻优设计方法

4.1 复合目标函数构建

上文针对随机平移替代法会降低跳频序列平衡性的问题，引入组合跳变序列，提出了组合跳变随机平移法。此外，在构造宽间隔跳频序列的过程中，序列参数的选取不当可能导致序列的多个性能间出现失衡的情况，因此，本文将针对这个问题，提出基于粒子群算法的序列参数寻优设计方法，以实现在构造跳频序列的过程中兼顾多个性能。

本节在组合跳变随机平移法的基础上，通过构造复合目标函数，迭代计算最优的序列参数，实现宽间隔混沌跳频序列的宽间隔特性、平衡性和汉明自相关性的综合最优。

由3.2节可知，跳频序列的平衡性参数δ、汉明自相关性参数Ramax/R(0)越小，宽间隔特性参数Gap越大，那么跳频序列的各性能越好。因此构建复合目标函数如式(18)所示，复合目标函数F(L,q)越小，那么跳频序列的综合性能最优。

(18a)

(18b)

式中：L为序列长度；q为频隙数；α、β、γ为各性能的占比系数，其大小由各性能参数的取值范围决定，避免出现某一性能参数值过小而弱化对复合目标函数值的影响等情况。

4.2 基于粒子群算法的序列构造参数的迭代寻优

利用粒子群算法，对式(18)进行迭代计算，得到合适的序列构造参数L、q，具体步骤如下：

Step1 设置混沌映射初值x0、y0、z0，最小跳频间隔d。

Step2 设计复合目标函数F(L,q)。

Step3 引入粒子群算法，设置参数，根据图3所示流程构造宽间隔混沌跳频序列，以复合目标函数F(L,q)为优化目标对序列参数L、q进行寻优。

Step4 迭代计算得到寻优后的参数L、q。

Step5 利用迭代计算后的序列长度L、频隙数q构造基于CHRS的宽间隔混沌跳频序列，该跳频序列兼具优良的平衡性、汉明自相关性、宽间隔特性。

基于粒子群算法的序列构造参数寻优设计流程如图4所示。

图4 基于粒子群算法的序列构造参数寻优设计流程图

4.3 基于粒子群算法的序列构造参数寻优设计方法的性能评估指标

经粒子群迭代计算后，获得最优解L′、q′，根据图3所示流程构造宽间隔混沌跳频序列X。若序列X的平衡性参数为δ′，汉明自相关性参数为(Ramax/R(0))′，平均跳频间隔为Gap′，定义跳频序列的衡量因子如下：

(19)

(20)

(21)

a1、a2、a3越大且相互间相差越小，则本节所提方法产生的宽间隔混沌跳频序列的综合性能越好，即兼具优良的平衡性、汉明自相关性和宽间隔特性。因此，本文将通过仿真计算a1、a2、a3三个衡量因子来验证基于粒子群算法的序列构造参数寻优设计方法的有效性。

5 仿真与分析

5.1 CHRS宽间隔设计方法仿真

为验证CHRS方法的有效性，本节利用Matlab软件，分别采用CHRS方法和RSR方法产生两组宽间隔混沌跳频序列，计算两组序列的平衡性、汉明相关性、复杂度、初值敏感性、宽间隔特性、序列数目，比较其性能。

根据文献[6,8]，仿真参数设置为x0=0.400 00，y0=0.400 01，z0=0.400 02，d=3，q=32，L=[128,256,512,768,1 024,1 280,1 536,1 792,2 048,2 506,3 000,4 096]。

5.1.1 平衡性

CHRS方法和RSR方法产生的宽间隔混沌跳频序列的平衡性如图5所示，可以看出通过CHRS方法构造的宽间隔混沌跳频序列的平衡性更好。

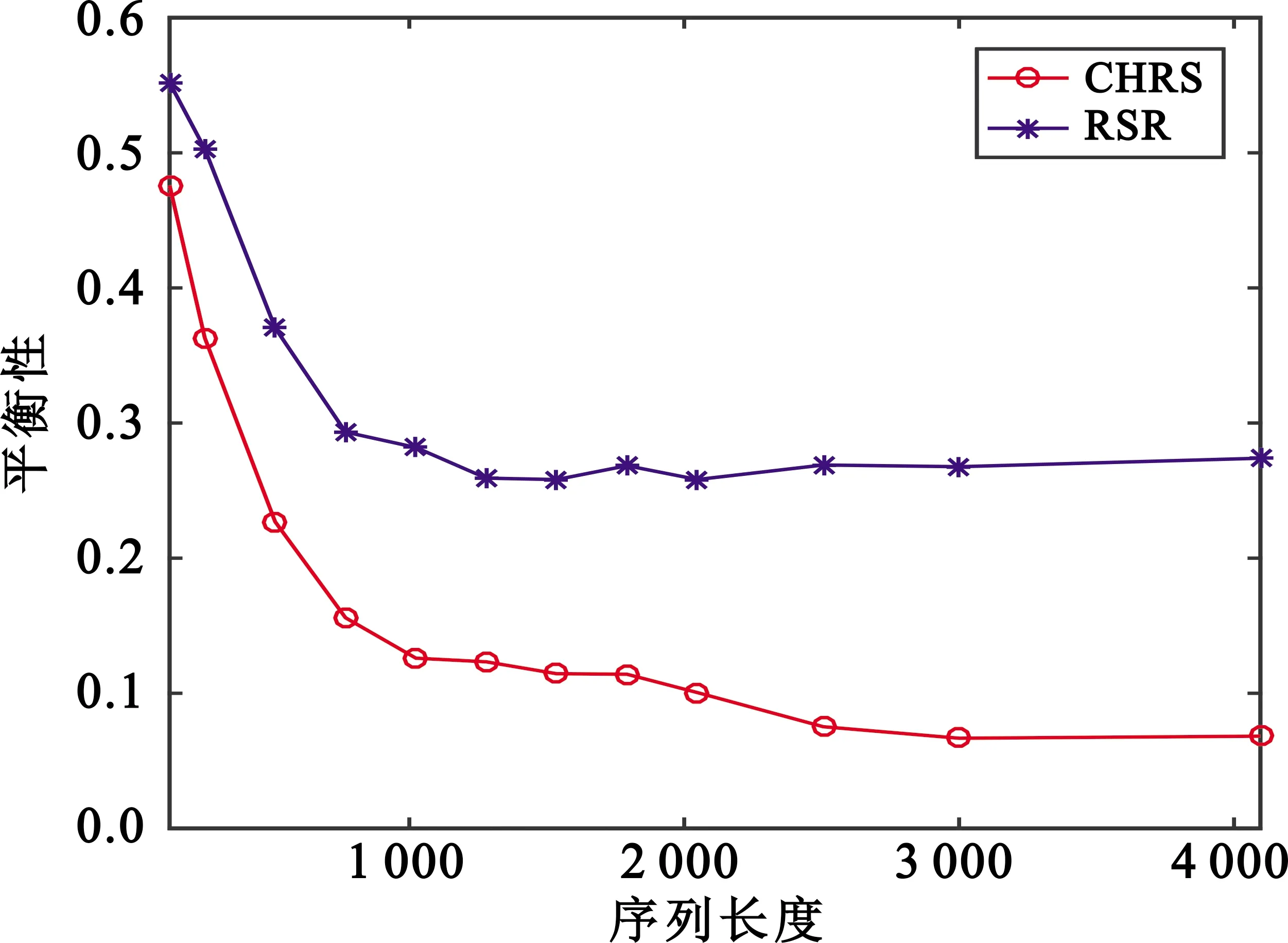
图5 平衡性

5.1.2 汉明相关性

CHRS方法和RSR方法产生的宽间隔混沌跳频序列的汉明自相关性如图6所示，可见通过CHRS方法构造的宽间隔混沌跳频序列的汉明自相关性更好。

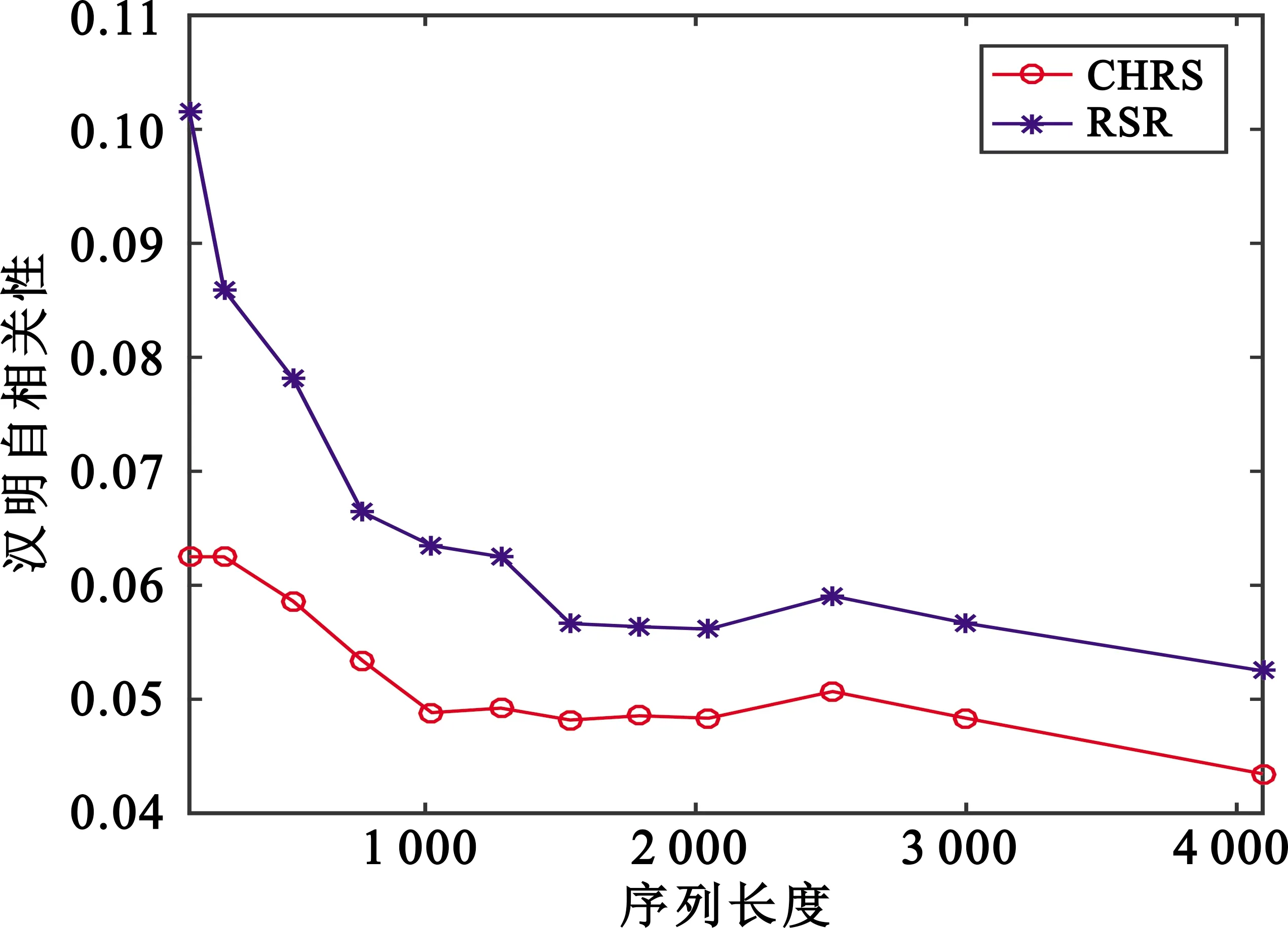
图6 汉明自相关性

CHRS方法和RSR方法产生的宽间隔混沌跳频序列的汉明互相关性如图7所示，通过CHRS方法构造的宽间隔混沌跳频序列的汉明互相关性更好。

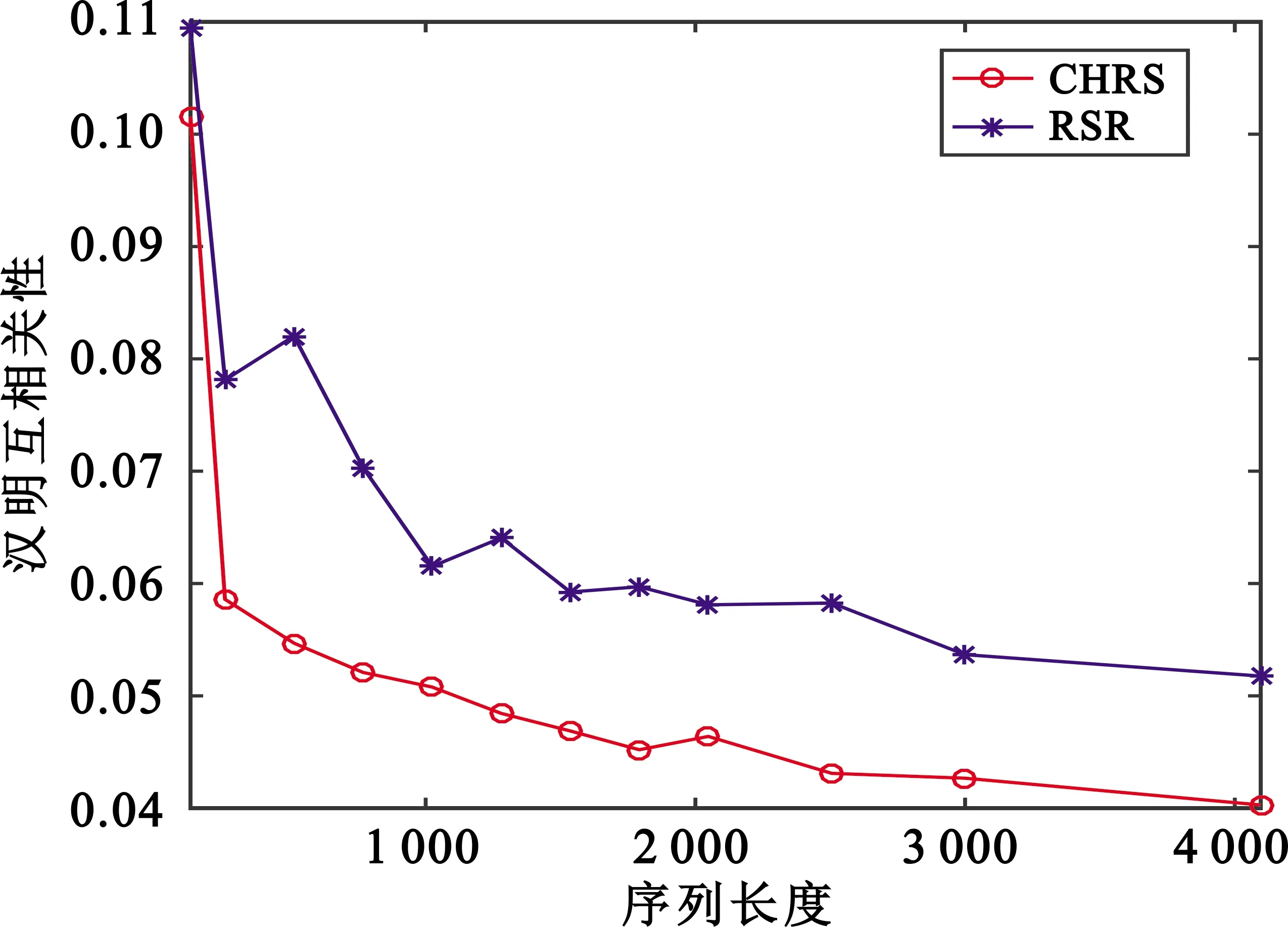
图7 汉明互相关性

5.1.3 复杂度

CHRS方法和RSR方法产生的宽间隔混沌跳频序列的近似熵如图8所示，可见当序列长度超过1 000后，通过CHRS方法构造的宽间隔混沌跳频序列的近似熵更大，即序列的复杂度更高。

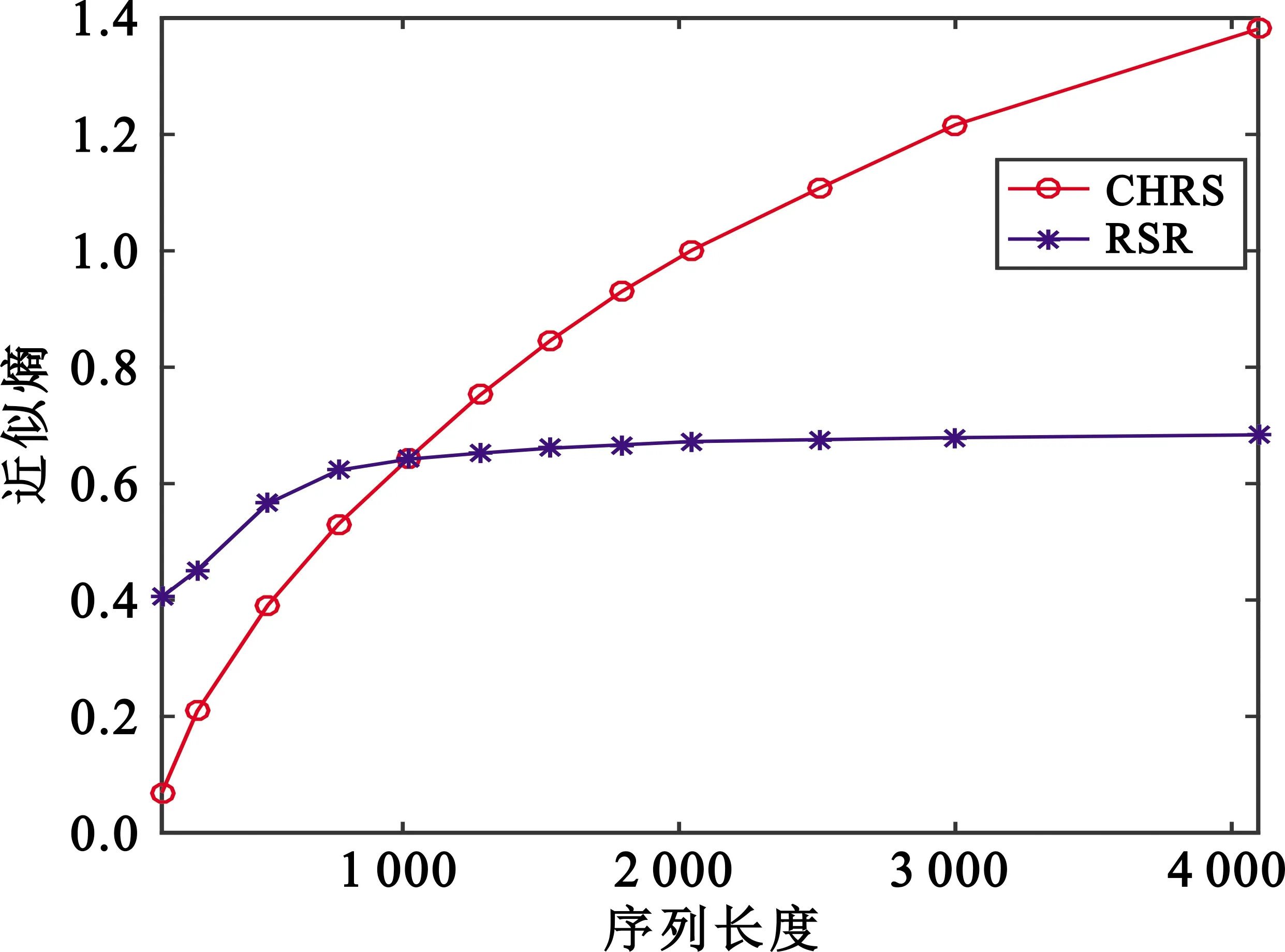
图8 复杂度

5.1.4 初值敏感性

CHRS方法产生的宽间隔混沌跳频序列的初值敏感性如图9所示，可见在经过大约10次迭代之后，初值相差很小的两个基于CHRS方法产生的宽间隔混沌跳频序列完全不同，具有很好的初值敏感性。

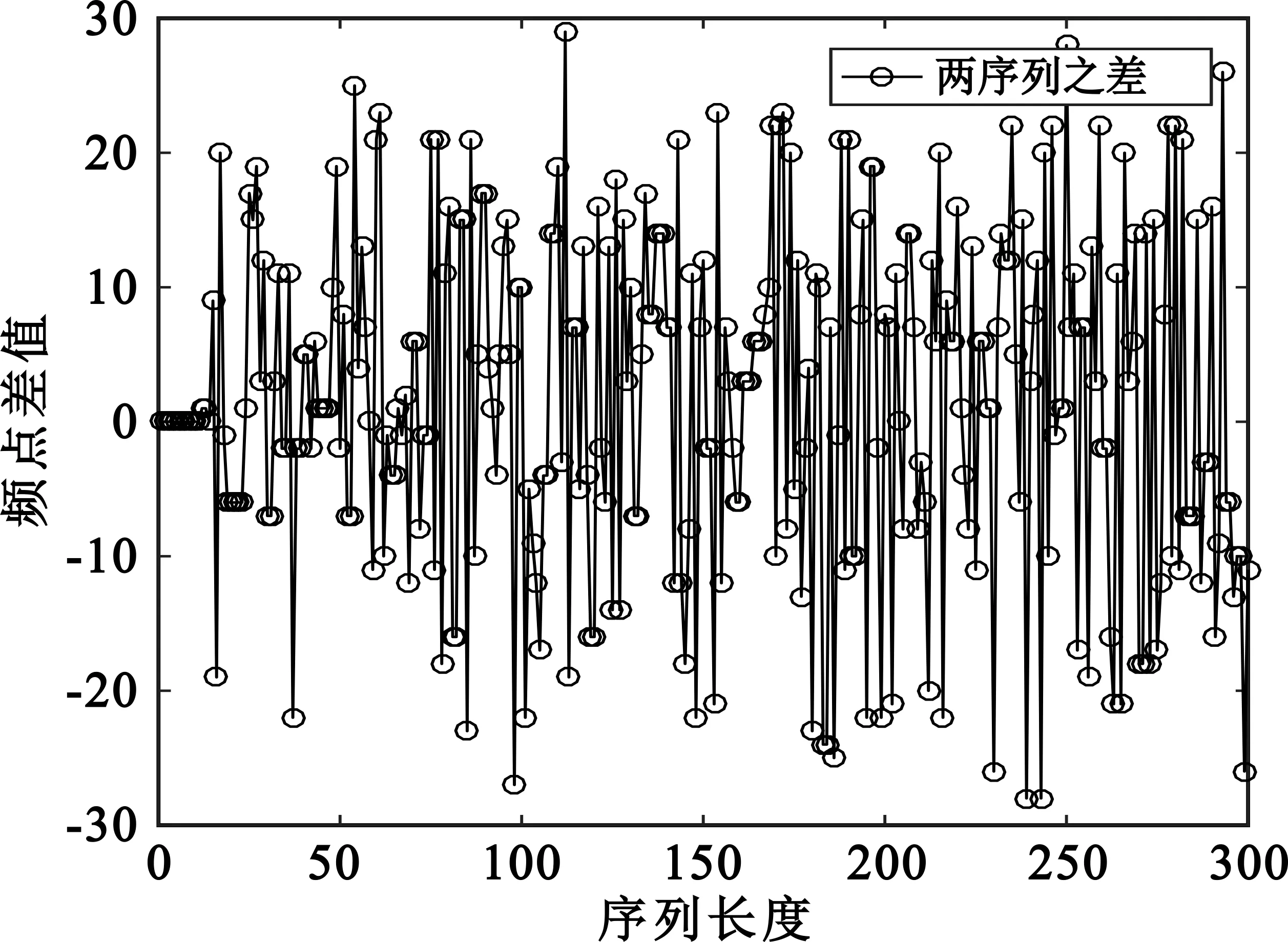
图9 初值敏感性

5.1.5 序列数目

表1 CHRS与RSR方法构造的跳频序列数目

5.1.6 宽间隔特性

基于CHRS方法和RSR方法产生的宽间隔混沌跳频序列的平均跳频间隔如表2所示，可见CHRS方法产生的跳频序列的宽间隔特性比RSR方法差，但仍满足宽间隔要求。

表2 跳频序列的宽间隔特性

5.2 基于粒子群算法的序列构造参数寻优设计方法仿真

为验证基于粒子群算法的序列构造参数寻优设计方法的有效性，按照图4所示流程图进行参数寻优，参数设置为x0=0.400 00，y0=0.400 01，z0=0.400 02，d0=3，Lmin=700，Lmax=900，qmin=20，qmax=50，α=2，β=γ=1。

经过粒子群迭代计算得到的序列参数构造的宽间隔混沌跳频序列与未经过粒子群寻优的序列的性能平衡因子如表3所示。

表3 经过粒子群寻优与未经过寻优的序列的衡量因子

由表3可知，经过粒子群迭代计算得到的序列参数构造的宽间隔混沌跳频序列的综合性能较优，各性能衡量因子均大于0.6，即兼具优良的平衡性、汉明自相关性、宽间隔特性；但该方法计算量较大，存在实时性差的问题。

6 结束语

宽间隔跳频序列设计是提高跳频系统抗干扰性能的重要途径。本文以构造性能优良的宽间隔混沌跳频序列为目标，首先基于随机平移替代法提出一种新的组合跳变随机平移法。该方法相对于随机平移替代法，有效地提高了宽间隔混沌跳频序列的平衡性、汉明相关性、复杂度，增加了可以构造的序列数目，并具有良好的初值敏感性。在此基础上，本文提出基于粒子群算法的序列构造参数寻优设计方法，通过计算最优控制参数，实现宽间隔跳频序列的平衡性、汉明自相关性、宽间隔特性的均衡最优。但该方法存在耗时久的问题，所以提高该构造参数寻优设计方法的实时性将是下一步工作的重点。