航空发动机在翼清洗时机Wiener预测模型研究
闫 锋,姚星宇
(中国民用航空飞行学院航空工程学院,四川 广汉 618307)
1 引言
航空发动机使用过程中难免出现发动机内涵气路部件积污的情况,发动机性能和经济性将会变差,航空公司通常采用发动机在翼清洗的方法来改善发动机的性能。
厂家的清洗工作建议是以固定时间间隔(如1000飞行小时)给定的,这种方式的优点是工程管理简单,维修时间易于控制,其缺点在于发动机的清洗效能没有充分评估,可能会出现发动机性能状态良好,不需要开展清洗工作,而频繁实施清洗,导致维护过剩造成浪费。也可能会出现发动机在固定清洗节点前,性能已经衰退至临界值,需要提前开展清洗工作,导致航班计划以及维修保障计划改变[1-4]。
利用发动机性能参数(EGTM),基于节省燃油量成本、延长发动机在翼时间而节省的大修成本及清洗成本三者总和最小,得到发动机清洗参数门阀值,通过Wiener 退化模型模拟发动机EGTM在翼衰退规律,进而预测最佳清洗时机,最终实现由传统固定清洗时间间隔到柔性时间清洗间隔转变。
2 发动机清洗门阀值确定
2.1 发动机EGTM衰退模型
某航空公司某台发动机时间与对应的清洗EGTM 值数据,如表1所示。

表1 航空发动机清洗数据Tab.1 Aero-Engine Cleaning Data
利用回归分析得EGTM 衰退模型:

式中:yi—EGTM;xi—在翼时间,可取为飞行小时数;k1,k2—回归系数,是随机变量,与样本有关;k1—衰退率;ε(x)i—随机干扰项。经过数据处理后可以得到EGTM与飞行小时数的关系为:y=-1.83x+55.2。
2.2 改变门阀值后延长在翼时间与节省大修成本计算
简化发动机衰退模型如下:
假设1:清洗前后EGTM衰退率不变。
当发动机清洗的门阀值改变后相应的发动机的在翼时间也会随之改变,由此可以通过改变发动机清洗门阀值的新清洗方式来延长发动机在翼时间从而节省发动机大修成本。
假设2:改变门阀值的量为ΔEGTM,基于假设1可以得到改变发动机清洗门阀值后与原始数据的对比图,如图1所示。

图1 改变阀值对比图Fig.1 Comparison Chart for Changing Threshold
发动机大修时间间隔约为20000飞行小时,大修成本约为发动机新机价格的三分之一。
当延长发动机清洗门阀值后由对比图及数据公式可见延长了发动机的在翼时间为( ΔEGTM/K )*2,式中:K—发动机EGTM衰退率,K=1.83。则通过延长清洗门阀值后节省发动机大修成本为( ΔEGTM/1.91 )*136000美元。
2.3 节省燃油量计算
2.3.1 节省燃油量计算模型
参考文献[5]给出了节省燃油量计算方式及发动机清洗前后DFF与飞行循环间函数关系,如图2所示。

图2 节油模型图Fig.2 Fuel-Saving Model Diagram
图2参数注释及单台发动机节省燃油具体算法公式如下:
发动机清洗后巡航消耗燃油偏差量量增量=30台发动机清洗前燃油偏差量平均值-30台发动机清洗后燃油流量偏差值平均值。
燃油偏差量恢复清洗前飞行循环间隔由起飞时EGTM变化所对应的飞行循环间隔来计算,依据如下:
(a)燃油流量偏差值测量时更分散;
(b)EGTM值测量更加准确;
(c)发动机性能变化在起飞时能够更好体现。
单台发动机节省燃油量公式可表示为:
一次飞行循环节油量=总面积*发动机一次巡航燃油消耗量
其中,总面积=1.2*S1
鉴于某型航空发动机相较于罗罗公司的发动机性能衰退率更低一些,故总面积约为1.1倍的S1。
2.3.2 单台发动机节省燃油量计算实例
由已知数据可知发动机清洗后燃油流量偏差变化量为0.43,且EGTM恢复至清洗前飞行循环的时间间隔为34700h。由此可知S1=34700*0.43=14921,总面积为17905.2,且发动机单次平均每小时耗油2.7吨约964美元。综上数据可知单台发动机清洗后节省燃油流量的成本为1726万美元。
2.4 基于总成本最低的发动机清洗门阀值确定
发动机的总成本是需综合考虑发动机大修成本、发动机燃油消耗成本及发动机清洗成本三个因素,发动机总成本为上述三者之和。
改变发动机清洗门阀值后的节约发动机燃油量情况不变,发动机清洗成本为6000美元左右。发动机清洗门阀值的改变主要影响发动机大修成本(在翼时间改变)。改变清洗门阀值后节约的发动机大修成本随ΔEGTM的增大而增大,发动机总成本相应的随节省的发动机成本增大而减小,即当发动机大修成本节省值最大时发动机总成本最低。发动Q机的EGTM大修限定值为20℃,为保证发动机安全性则保证发动机的EGTM值衰退到19℃前应得到及时清洗,且保证清洗次数和图中曲线一直,所以基于发动机节约成本最低情况下ΔEGTM值应为0.6℃。
综上所述首次发动机清洗门阀值确定在33.6℃。
3 发动机在翼清洗时间预测wiener模型
发动机EGTM性能衰退的Wiener模型如下[6]:

式中:μ—漂移参数;σ—扩散系数;W0(t)—标准Wiener过程其中各参数为E[W(t)]D[W(t)]=σ2t。
3.1 模型参数估计
发动机性能退化的似然函数[7]:

对上式μ和σ分别求偏导可得:

3.2 贝叶斯参数更新
参数更新方程如下:

式中:f(μ),f′(θ)—μ和θ先验概率密度函数;f(μ,θ|x)—后概率密度函数;D(μ),D(θ)—μ和θ取值范围;g(x|μ,θ)—似然函数。设σ2=1/θ2通常检测的间隔相同,即Δtij=Δt,xij=ΔWij/Δt,则似然函数可以写成:

4 清洗时间的预测模型
发动机剩余清洗时间T是退化量W(t)首次达到清洗阈值的时间,可以表示成:

根据文献T服从逆高斯分布IG(l/μ,l2/σ2),T的分布函数和概率密度函数分别为:

通过Wiener过程参数更新,得到μ和σ2估计的更新值和,其中σ2=1/θ2,t时刻的发动机性能水平:

5 仿真实例
5.1 仿真计算
选取某航空公司发动机的EGTM数据,如表2所示。

表2 发动机飞行小时对应的EGTM数据Tab.2 EGTM Data for Engine Flight Hours

可求得参数估计值,如表3所示。

表3 参数估计Tab.3 Parameter Estimation
图3中f1、f2和f3分别表示发动机在1500飞行小时、2000飞行小时和3000飞行小时时预测的剩余清洗时间分布。根据固定参数法可得发动机剩余清洗时间概率密度函数曲线,如图3所示。
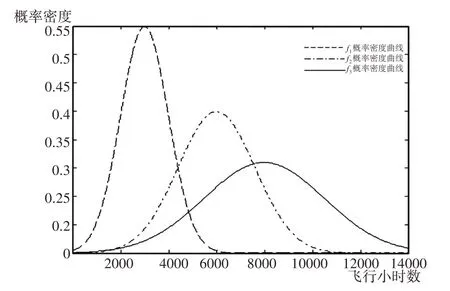
图3 发动机剩余清洗时间概率密度函数的预测Fig.3 Prediction of Remaining Engine Cleaning Time Probability Density Function
由剩余清洗时间概率密度函数积分可得发动机预测的剩余清洗时间,如表4所示。

表4 发动机清洗预测值与实际值对比Tab.4 Comparison Between Predicted Value and Actual Value of Engine Cleaning
5.2 模型验证
某航空公司选择40架同型飞机的80台发动机,并将其他未选中的108架飞机作为对比组。采用新方法试运行一年,发动机清洗维修间隔可以偏离现有维修方案规定的1000发动机飞行小时,但最高不得超过1600飞行小时。两种机队试运行的数据情况,如图4所示。该方法清洗发动机衰退速率较慢,即说明该方法较好。

图4 两种清洗方法对比Fig.4 Comparison of Two Cleaning Methods
6 结论
根据某航空公司发动机清洗前后EGTM 数据,得到发动机的性能衰退模型,依据Rolls-Royce公司的节省燃油量模型,基于总成本最低的发动机清洗门阀值,可得首次发动机清洗门阀值(EGTM)为33.6℃。依据Wiener预测模型和贝叶斯更新理论,确定Wiener预测模型的参数,最后通过发动机剩余性能概率密度函数可得给定飞行小时的预测剩余清洗时间,最后分析某公司机队运行数据,结果表明用新方法清洗的发动机性能衰退较慢,本方法较好。

