改进EEMD 与ICA 算法的水电机组振动信号特征提取
张新华,钟 永,袁 翔,杨峰雄,付向涛
(1. 国家电力投资集团水电产业创新中心,湖南 长沙 410000;2. 五凌电力有限公司挂治电厂,贵州 锦屏 556700)
随着国家构建新型电力系统战略的提出,促进了水电行业进一步发展,水电机组的单机容量越来越大,水电机组安全稳定运行也越来越受重视。然而,水电机组振动受水力、电磁、机械、环境等各个方面因素影响,运行工况极其复杂。采集的振动信号受环境噪声、故障信息等因素相互叠加的影响,使得水电机组振动信号早期包含的故障特征易被环境噪声所湮没,这些因素都制约水电机组振动信号特征提取。目前,水电机组振动信号特征提取方法主要包含:频率分析法、小波包特征提取方法、经验模态分解(EMD)分析方法[1]。频率分析方法对于平稳信号的分析有较好的效果,对于水电机组振动这种非平稳信号分析效果不佳;小波包分析方法具有时频两相性特征,但本质上仍是一种线性变换,且小波基的选取和分解层数具有不确定性,无法自适应地进行信号特征提取;EMD 是一种自适应信号分析方法,但EMD 分解受端点效应的影响,信号处理过程存在失真现象。以上方法在特定情况下,对于信号特征提取有很好效果,但不具备对复杂非平稳信号的特征提取[2]。
文中提出一种基于改进 EEMD 与独立成分分析(ICA)的水轮机振动信号特征提取方法。首先针对EEMD 算法存在的端点效应问题;提出一种基于镜像延拓的改进EEMD 算法,用改进的EEMD 算法对水轮机振动信号进行处理,得到一系列固有模态函数(Intrinsic Mode Function,imf)分量;其次,对主要imf 分量进行重构并和原始信号一起作为ICA 算法的输入信号,进行ICA 算法分析处理,对ICA 算法处理的信号进行频谱分析;最后以ICA 算法处理信号的频谱作为水轮机振动信号信号特征,用以研究水轮机振动状态变化规律,以指导机组检修。
1 改进EEMD 方法
1.1 EEMD 方法
EEMD 方法是在EMD 分解信号基础上,加入一组均值为零、方差相等的随机白噪声序列。EEMD同样是利用三次样条插值函数求取信号上、下包络。但三次样条插值函数拟合信号包络线过程中,在信号端点处易发散,在第1 个imf 分量的端点位置产生误差,原始信号减去第1 个imf 分量的余项是第2 个imf 分量。在筛分的过程中,三次样条插值拟合的误差使端点向信号内部扩散,造成虚假的imf分量。尤其是当信号较短时,端点效应会使得EMD和EEMD 的分解结果失去意义,严重影响信号分解的质量。对于复杂的、非平稳的信号,需要进行多次EMD、EEMD 分解,端点效应的扩散会从第1 个imf开始,逐渐放大,严重干扰信号特征提取,造成分解结果失真[3]。
1.2 端点效应及其常用改进方法
EEMD 在用三次样条法拟合上下包络线时,在信号两端点出现较大的发散,造成失真现象,这就是所谓的端点效应。若端点效应不加以抑制,会使得分解结果失去意义。
目前,针对如何抑制端点效应,提出了许多解决方案。刘忠 等[4]提出极值延拓算法,以信号的极值点为依据,对信号进行延拓,在信号2个端点处,向外延拓2个极大值点和2个极小值点。蒋文君 等[5]提出基于EEMD 的特征提取方法,通过EEMD 自适应的白噪声抑制原有信号的噪声,改善EMD 分解结果,从而达到改善EMD 的端点效应的目的;徐力彬 等[6]提出基于镜像延拓与窗函数相结合的算法,通过窗函数改变信号端点,从而抑制其发散。广大学者在抑制端点效应效果方面虽然提出了很多解决方案,但这些方案也存在突出的问题,包括:延拓后的端点依然是不确定的,这导致拟合后的包络线在信号端点处依然是发散的;EEMD 这种改进算法依然采用的三次样条插值,并没有算法从本质上解决端点效应问题;此外,窗函数会改变原有信号的特征和窗函数本身缺乏自适应性。
1.3 基于镜像延拓的改进EEMD 方法
其改进算法的流程图如图1 所示。

图1 改进EEMD 算法
首先:(1)对信号x(t)进行镜像延拓。基本原理是:①找到信号左、右端的第1 个极值点;②利用镜像延拓,将信号左端点至左端第1 个极值点的信号、右端点至右端第1 个极值点信号对称延拓,通过延拓使信号的端点向外延伸,增加了可处理数据的长度,从而提高EEMD 的分解精度。(2)将一组均值为零、方差相等的随机白噪声序列加入延拓后的信号,得到复合信号x’(t)。(3)采用EMD 算法对复合信号x’(t)进行分解。分解后得到n组imf 分量[imf1,imf2,…,imfn],和m组余量[r1,r2,…,rm]。(4)截断镜像延拓部分信号后,作为原始信号x(t)最终的分解结果。根据文献[7,8],用相关系数ri来表征各imf分量与原始信号的相似度,以此来评价EEMD 的抑制效果,相似度越高,端点效应的抑制效果越好。

1.4 仿真分析
为了检验改进EEMD 方法的有效性,对仿真信号进行镜像延拓后对其进行EEMD 分解,最后再舍去延拓部分。仿真信号x(t)为:x(t)=50 sin(200×pi×t)+20 sin(100×pi×t)+sin(40×pi×t)。x(t)选取1 001 个点。
仿真信号、镜像延拓信号和EEMD 处理结果如图2 所示。从图2 可以看出,各imf 分量端点没有出现明显的发散现象,端点效应得到了较好的抑制。

图2 仿真信号分解结果
为进一步验证端点效应的抑制效果,用传统EMD 算法、极值延拓算法对该仿真信号进行分解处理。传统EMD 算法、极值延拓算法和文中改进算法分解信号后得到的相关系数见表1。
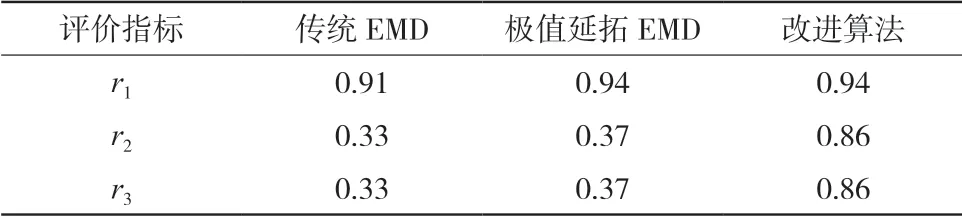
表1 端点信号抑制效果比较
从表1可以看出,传统EMD 方法处理结果的相关系数最小;极值延拓与算法改进后的得到分解结果,其相关值有不同程度增大;从表中可以发现:随着分解层数的增加,端点效应逐步发散,其相关系数逐渐降低;根据改进EEMD 方法得到的3 个相关系数均大于0.8,对端点效应抑制效果最为明显。
2 独立分量分析
ICA 分析的目的是对任何已知测得的信号x(t),在任何混合矩阵W未知情况下,求出未知信号源s(t),固有矩阵模型为:

在进行ICA 分析之前,先对信号进行白化处理,以改善算法的计算性能。
设C为一个信号x的协方差样本矩阵,有:

式中将x进行奇异值分解,U、V0为左右奇异矩阵,δ为信号C特征值构成的对角阵,∑0为信号x奇异值组成的对角矩阵。令Z为:

则有:

由式(5)可知,Z为单位正交矩阵,这一过程称为白化处理[9-11]。
3 水电机组振动信号特征提取
3.1 基于改进EEMD 与ICA 的特征提取方法
针对传统时频特征分析方法难以准确分析故障特征,提出基于改进EEMD 与ICA 的特征提取方法。其算法流程如图3 所示。

图3 特征提取流程图
具体步骤为:①首先采用改进的EEMD 算法对信号进行处理,分解得到imf 分量;②选择与原信号相关系数较大的imf 重构虚拟通道,与原信号一起输入ICA 算法。③对ICA 算法计算得到的输出分量进行FFT 变换,分析其频谱特征。
3.2 水电机组振动信号的分析
国内某水电机组大修前,发现定子基座振动信号偏大,其水轮机参数:轴流转桨式机组,导叶24片,设计水头320 m,额定转速115.4 r/min。选用豪瑞斯振动传感器MLS-V9,安装于定子基座X、Y 方向。采集信号时机组在变负荷工况下运行,截取其中一段数据共4 325 个点进行研究。原始信号如图4 所示,用改进EEMD 算法分解信号结果如图5 所示,ICA 算法输出信号及其频谱如图6 所示。

图4 实测信号

图5 改进EEMD 分解

图6 ICA 算法输出信号及其频谱
由图5 的分解结果可以看到,改进算法分解得到的imf,其两端并没有出现明显的发散现象,表明该算法对端点效应的抑制是有效的。
由图6 可知,改进EEMD-ICA 算法提纯了水轮机组的振动信号,并成功提取了机组的频率信息。
从图6 可以明显看到,机组振动信号频率中出现了1/2 倍频以及整数倍频。由水电机组故障诊断集可知,在机组变负荷过程中,存在转子动不平衡、质量不平衡以及尾水管涡带、压力脉动较大等工况时,频谱表现为1/2 倍频和整数倍频,初步判断,机组振动主要由尾水管压力脉动产生。在机组解体过程中发现,压力脉动作用结果表现在转轮叶片上形成大面积空蚀,如图7 所示,实际结果表明所提出的算法可以提取水轮机组微弱故障信号。

图7 转轮叶片上形成的空蚀
4 结论
(1)文中提出的基于镜像延拓的改进EEMD 方法充分结合镜像延拓和EEMD 算法的优势,避免传统EMD 算法分解过程中存在端点效应问题和分解过量的问题。
(2)基于改进EEMD-ICA 算法能够自适应消除信号的噪声,将其应用于水轮机组故障特征提取,该方法保留信号的原始特征,避免频谱分析中噪声频率的干扰,用以指导现场检修。实践证明所提方法可以很好满足工程实践的需求。

