一种基于二进小波变换改进图像的去噪方法

马瑞瑞，王 刚，张 静

(新疆师范大学 数学科学学院，乌鲁木齐 830017)

在图像采集、传输和转换过程中，会加入一些噪声，如模糊、失真和噪声；而在实际应用中，需要清晰、高质量的图像。恢复图像最基本的任务是在不丢失图像细节信息的情况下去除图像中的噪声。[1-2]然而，抑制噪声和保持细节往往是矛盾的，这也是图像处理中一直没有很好解决的问题。为了获得模糊图像的清晰图像，传统的图像恢复算法通常对整个图像进行处理，信息全部被还原，使得需要的信息不够突出[3]。中值滤波去噪效果一般，且图像细节信息会有部分丢失。二进小波变换域内数据表达存在很大冗余性，便于对每个尺度下的细节和概貌进行频谱分析，可以有效避免由于非线性变换在边缘不连续时所引起的伪吉布斯现象。在相同误判概率下，二进小波变换可改变图像重建效果，降低图像在重建过程中产生的人工噪声，相比于其他去噪算法，二进小波变换的图像去噪方法对噪声水平有很强的稳定性[4]。针对这种情况，本文提出了一种基于B-样条二进制小波变换与中值滤波结合的方法，且提出基于B-样条与图像的加法相结合的方法，进一步说明了，构造的B-样条二进小波滤波器不仅能够达到很好的去噪效果，而且能够很好保留图像的细节信息。图1为本文的算法流程。

1 中值滤波

中值滤波是指使用固定的幻灯片窗口对图像进行过滤。基本上，当前像素的像素值用周围所有像素中的值来代替。如果有奇数，则使用中间值将偶数设为中间2位。与线性滤波相比，可以保留更多图像细节。另外，图像模糊也有一定的抑制效果。使用中值过滤器去除噪声时，根据图像的特征选择矩形、圆形、十字形、线性等形状，窗口大小有3×3、5×5、7×7、9×9等，通过测试从小到大，选择合适的窗口尺寸[5-7]。

具体步骤如下:

Step1:在模板中漫游图像，将模板中心和图像中心的一个像素重叠；

Step2:读取模板下各对应像素的灰度值;

Step3:将这些灰度值从小到大排列成一列;

Step4:找出排在中间的一个值;

Step5:将此中间值分配给相应模板的中心像素。

中值滤波的优点是保护图像边缘信息，去除图像中不需要的图像噪声；缺点是容易造成图像的不连续性。

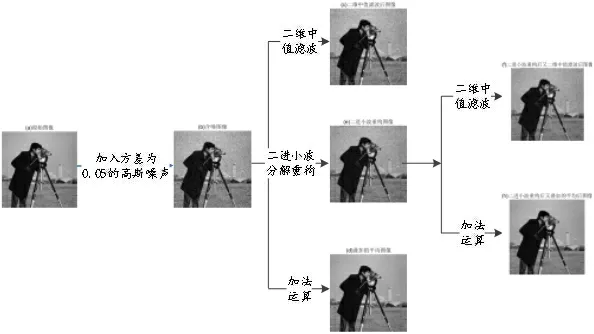
图1 本文算法流程图

2 图像的加法运算

图像相加的一个应用是生成一个图像的内容重叠在另一个图像上的图像效果，或者在图像中的各个像素点上叠加常数以改变图像的亮度。图像相加的另一个重要用途是通过重叠相同图像并平均化来去除原始图像中的附加噪声[1-2]，其原理是:对原始图像f(x,y)有一个噪声图像集{gi(x,y)}，i=1,2,…,M,其中：

(1)

M个图像的均值为

(2)

当噪声ei(x,y)不相关且均值为0时，上述图像均值会降低图像的噪声。

3 B-样条二进小波滤波器

3.1二进小波快速算法——｀aTrous

在对图像进行处理时，大部分是在对象为离散状况下进行的，所以需要用到二进小波变换的离散形式计算方法。在1992年，MALLAT创建了能够完成二进小波变换的计算方法，即｀aTrous算法，与MALLAT计算方法具有一样的优势，代表了不一样尺度的二进小波系数的联系。需要说明文中所提的｀aTrous算法是T.ABDUKIRIM在MALLAT创建的算法的基础上修改得到的。

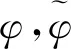
(3)

当j≥0时，记

aj[n]=，

(4)

其中：

对任意j≥0，在整数格点上，二进小波的系数计算方法为

dj[n]=(Wψ,f)(2-j,n)(t)=,n∈Z

。

(5)

也就是说任意尺度2j>1,{d1,d2,…，dj,aj}这一离散信号的序列便可以被叫作a0离散信号的二进小波变换。

定理1 二维｀aTrous算法[8-10]

二维DyWT分解公式

(6)

二维DyWT重构公式

(7)

其中:j=0,1,2,…

3.2B-样条二进小波滤波器的构造

此方法是对MALLAT的B-样条二进小波的推广[8-9]，过程是由T.ABDUKIRIM完成的。具体过程如下，m次B-样条函数φ(t)是特征函数χ[0,1]与其自身的卷积的平移:φ(t)=χ*χ*χ…χ[0,1](t)。

对φ(t)进行Fourier变换，可以得到

(8)

根据二尺度关系有

(9)

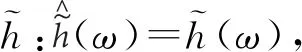
(10)

由二进完全重构有

(11)

因此由二尺度关系有

(12)

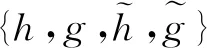
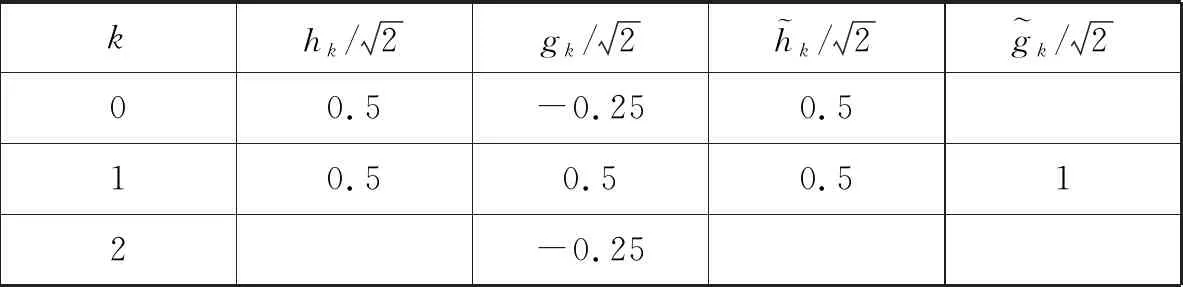
表1 r=2，m=0时的B-样条二进小波滤波器的系数

4 实验过程与分析

本实验是以MATLAB R2016a为实验平台，以标准的“cameraman.tif”图像加入方差为0.005的高斯噪声作为分析对象。实验过程是：首先，分别利用二维中值滤波和图像的加法运算对含噪图像去噪；其次，利用B-样条二进小波滤波器将图像分解一次重构，得到复原后图像；最后二进小波重构后图像分别再次进行二维中值滤波去噪和图像的加法运算去噪。

(1)图2(a)是MATLAP自带的“cameraman.tif”图像加入方差为0.005的高斯噪声图像，观察图像，可以看到，噪声密度较集中。

(2)图2(b)是对图像进行二维中值滤波后的图像，图像的细节信息没有突出，边缘不够清晰，人物的嘴巴几乎看不到，去噪效果一般。

(3)图2(c)是图像的加法运算。通过叠加相同的图像并取平均值，消除了原始图像中的附加噪声。这种方法在原图已知的情况下，通过叠加次数的增大，能够达到很好的去噪效果。但对原图未知的情况，达不到很好的去噪效果。

(4)图2(d)是用B-样条二进小波分解重构含有高斯噪声的图像，利用B-样条二进小波变换将图像分解一层，重构后的图像去噪效果明显强于传统的中值滤波，人物的嘴巴可以看到，这种方法更适于实际应用。

(5)图2(e)为本文方法1，先对图像进行B-样条二进小波分解重构，然后再对重构后的图像进行中值滤波，得到的图像效果要明显好于图(c)方法，比图(d)方法要好一些，图像细节也保留得较好。

(6)图2(f)为本文方法2，先对图像进行B-样条二进小波分解重构，然后再对重构后的图像进行叠加取平均，这种方法得到的去噪图像明显比图(e)去噪效果强，但和图(c)人眼很难对比出去噪效果，两者都能达到很好的去噪效果，并且这个方法更进一步说明B-样条二进小波滤波器能够很好地保留图像的细节信息。

(a)

(b)

(c)

(d)

(e)

(f)

为了使实验效果更加真实可信，求得图像信噪比，更加直观地看到每种方法的去噪效果，其中，图像信噪比越大，则图像去噪效果越强[11]。数据见表2。

表2 峰值信噪比

从数据中更能客观地说明本文提出结合二进小波与中值滤波效果更优于传统单一使用中值滤波的方法，因为加法运算可以达到很好的复原效果，所以将加法运算与二进小波结合，发现两者都可以达到很好的去噪效果，并且图像细节信息被很好地保留，更进一步说明了二进小波滤波器具有很好的去噪效果与保留图像细节信息的效果。

5 结语

本文将B-样条二进小波变换的特点和中值滤波的优势，以及图像的加法运算结合起来，提出基于B-样条二进小波变换的图像复原方法。人物图像的细节很多，边缘容易模糊，让所有有用的细节信息能够保留并且达到去噪的效果尤为重要。实验结果表明，用B-样条二进小波滤波器去噪效果远优于单纯地使用均值滤波传统方法的去噪效果，将B-样条二进小波滤波器分别与中值滤波以及图像的加法运算结合，结合的方法相较于单一使用的方法有一定提升。

在后续的工作中，将对小波分解后的低频子图和高频子图分别讨论。本文中去噪方法还需进一步提升，让去噪效果更佳，且细节可以用别的方法进行复原。本文也进一步证明了B-样条二进小波在图像去噪中的良好性能的同时，能很好地保留图像信息，为下一步二进小波的研究奠定了基础。