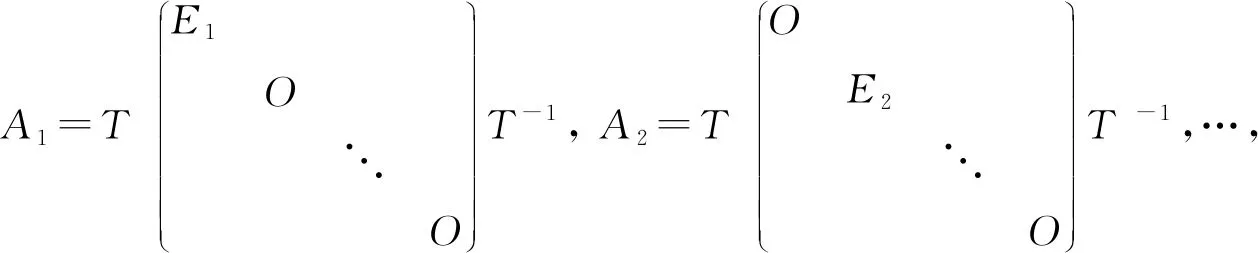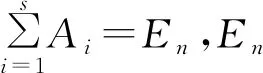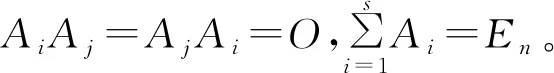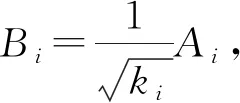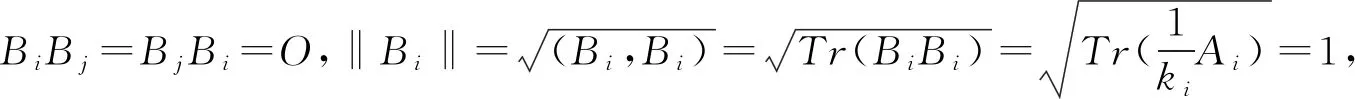矩阵按其特征值的和式分解

杨衍婷，阳 静，郭佳乐，孙远航，高 宇，陈雄涛

(咸阳师范学院 数学与统计学院，陕西 咸阳 712000)

0 引言

把矩阵分解为形式比较简单或具有某种特性的一些矩阵的和，在矩阵理论的研究与应用中是非常重要的。这些分解式的特殊形式一方面能反映出原矩阵的某些数值特征，另一方面分解的方法与过程给研究者提供了有效的理论分析依据。在矩阵的和式分解中，谱分解理论在代数学中占有重要地位。高枫[1]给出了单纯矩阵的谱分解及其谱族的构成方法；林志兴等[2]给出了不需要求出特征值和特征向量的幂幺矩阵的谱分解的计算公式；李大林[3]提出了亏损矩阵广义谱分解概念,所得广义特征矩阵具有类似若当链的性质，并介绍了广义谱分解在计算矩阵幂级数中的应用。另外，矩阵和式分解并不局限于谱分解，它方法灵活，应用广泛；杨尚骏等[4]研究了矩阵分解为稳定矩阵之和的问题；王岩等[5]讨论了矩阵分解为若干矩阵的乘积或和的一些应用。矩阵和式分解涉及数值计算和数据处理的诸多方面，已经广泛应用于计算机科学、信息科学等领域。

本文利用代数构造的方法研究任意复数矩阵按其特征值的和式分解及分解的唯一性问题，以设计出简单矩阵来表达复杂矩阵，使得计算简单，满足实际中对数据处理的实时性要求，并且可以为理论分析提供一定帮助。

1 相关引理

引理1 设A,B均是可对角化的n级方阵，且AB=BA，则存在可逆矩阵T，使TAT-1与TBT-1均是对角矩阵。

证明 请参阅文献[6]。

引理2 设n级复数矩阵A可表示为

A=λ1A1+λ2A2+…+λsAs，

其中：AiAj=AjAi，Ai可对角化，则A可对角化。

证明 运用数学归纳法证明。

当s=1时，结论显然成立。

假设当s=k时，结论成立，则当s=k+1时，根据假设，λ1A1+λ2A2+…+λkAk可对角化，由已知，Ak+1可对角化，Ak+1Ai=AiAk+1(i=1,2,…，k)，则

Ak+1(λ1A1+λ2A2+…+λkAk)=(λ1A1+λ2A2+…+λkAk)Ak+1。

根据引理1，存在可逆矩阵R，使得

其中：μ1,μ2,…,μn为λ1A1+λ2A2+…+λkAk的特征值，δ1,δ2,…,δn为Ak+1的特征值，则

即λ1A1+λ2A2+…+λkAk+λk+1Ak+1可对角化，从而当s=k+1时，结论成立，这样，可得引理2成立。

2 结论及证明

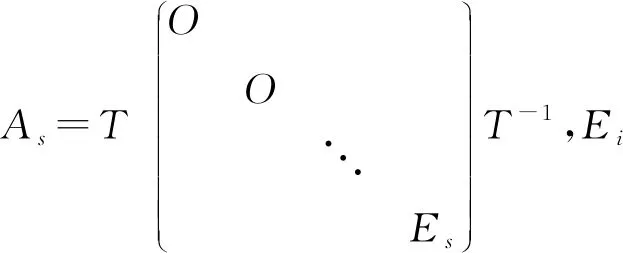
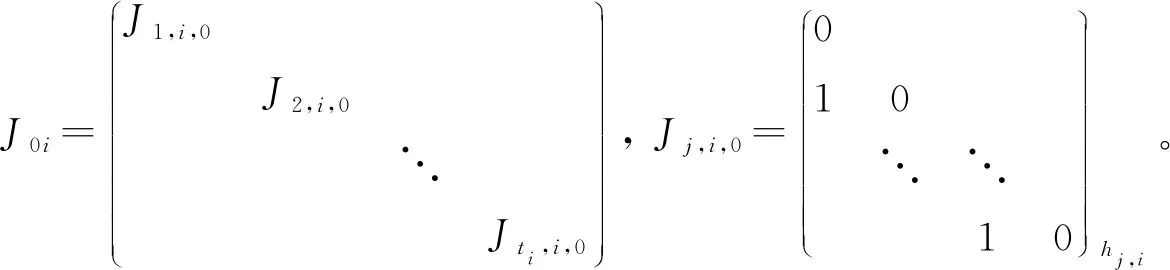
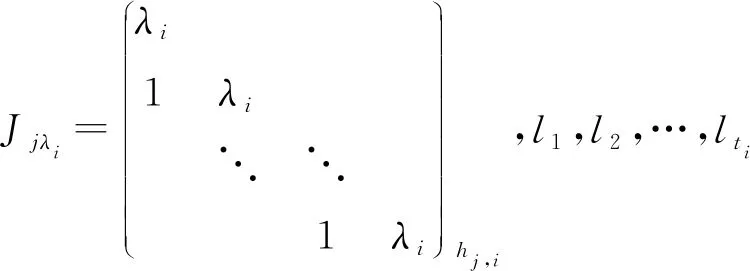
定义1 对于两个不相等的二维实向量(x1,y1)与(x2,y2)，当x1

根据定义1，两个不同复数λ=|λ|(cosα+isinα)，μ=|μ|(cosβ+isinβ)，当(|λ|，α)(|μ|，β)时，规定λμ，其中，0≤α<2π，0≤β<2π。

定理1 设A是复数域C上的一个n×n矩阵，则A可以唯一分解为

A=λ1A1+λ2A2+…+λsAs+B。

其中，λ1,λ2,…，λs是A的全部互不相同的特征值，且λ1λ2…λs，Ai是幂等矩阵，Ai的秩为λi的代数重数，为n级单位矩阵，且当i≠j时，有AiAj=AjAi=O，B是幂零矩阵，且有BAi=AiB。

证明 因为n级复数矩阵A与它的若当标准形相似，即存在可逆矩阵T，使

根据矩阵分块运算，有

A=λ1A1+λ2A2+…+λsAs+B，

且Ai2=Ai，当i≠j时，AiAj=AjAi=O，Ai的秩等于Ji的级数，从而为λi的代数重数。 因为Jj,i,0为幂零矩阵，所以B是幂零矩阵。 同时可以验证BAi=AiB。

下面证明分解式的唯一性。因为复数域上的n级方阵A的若当标准形除去若当块的排列次序外是被矩阵A唯一决定的，因此，当λ1λ2…λs(s≥2)时，设A的两个不同的若当标准形分别为

其中：

而

设有可逆矩阵T,Q使得

A有两种分解式

A=λ1A1+λ2A2+…+λsAs+B=λ1C1+λ2C2+…+λsCs+D。

其中：

根据若当形矩阵的特性,T=(T1,T2,…，Ts),Q=(Q1,Q2,…，Qs) ，其中：

Ti=(αi,1,(A-λiE)αi,1,…，(A-λiE)h1,i-1αi,1,…，αi,ti,(A-λiE)αi,ti,…，(A-λiE)hti,i-1αi,ti)，

Qi=(βi,l1,(A-λiE)βi,l1,…，(A-λiE)hl1,i-1βi,l1,…，βi,lti,(A-λiE)βi,lti,…，(A-λiE)hlti,i-1βi,lti)，

(A-λiE)h1,iαi,1=0,…，(A-λiE)hti,iαi,ti=0，(A-λiE)hl1,iβi,l1=0,…,(A-λiE)hlti,iβi,lti=0。

设σ=max{h1,i,h2,i,…，hti,i},则

αi,1(A-λiE)αi,1,…，(A-λiE)h1,i-1αi,1,…，αi,ti,(A-λiE)αi,ti,…,(A-λiE)hti,i-1αi,ti

是线性方程组(A-λiE)σiX=0的解。

同样，

βi,l1,(A-λiE)βi,l1,…,(A-λiE)hl1,i-1βi,l1,…,βi,lti,(A-λiE)βi,lti,…,(A-λiE)hlti,i-1βi,lti

是线性方程组(A-λiE)σiX=0的解。

当s≥2时，n-秩(A-λiE)σi=h1,i+h2,i+…+hti,i，于是

αi,1,(A-λiE)αi,1,…,(A-λiE)h1,i-1αi,1,…,αi,ti,(A-λiE)αi,ti,…,(A-λiE)hti,i-1αi,ti

和βi,l1,(A-λiE)βi,l1,…,(A-λiE)hl1,i-1βi,l1,…,βi,lti,(A-λiE)βi,lti,…,(A-λiE)hlti,i-1βi,lti

分别是线性方程组(A-λiE)σiX=0的基础解系，从而可以相互线性表示，所以存在可逆矩阵Si，使得Qi=TiSi，故

则B=D，从而分解唯一。

当s=1时，根据Ai的构造，可知Ai=A1=En，故分解唯一，因此定理得证。

定理2n级复数矩阵A可对角化的充分必要条件是

A=λ1A1+λ2A2+…+λsAs。

证明 必要性：

由引理2，λ1A1+λ2A2+…+λsAs可对角化。因为BAi=AiB，AiAj=AjAi，则(λ1A1+λ2A2+…+λsAs)A=A(λ1A1+λ2A2+…+λsAs)，A可对角化，根据引理2，则A-(λ1A1+λ2A2+…+λsAs)可对角化，即B可对角化，B为幂零矩阵，所以B=O。

充分性： 根据引理2可得。

推论1 设V是实对称矩阵构成的实线性空间，对于任意的A,B∈V，定义V中的内积运算为

(A,B)=Tr(AB),

则V中每个元素A均可写成

其中：λ1,λ2,…，λs是A的全部互不相同的特征值，数k1,k2,…，ks为A的对应着特征值λ1,λ2,…，λs的代数重数，且B1,B2,…，Bs是V的标准正交向量组。