基于惯性基准法的轨道高低不平顺影响分析

刘堂辉，刘锦辉，冯青松，许晨霄，刘文武，罗信伟

（1. 广州地铁设计研究院股份有限公司，广州 510010；2. 深圳市地铁集团有限公司，深圳 518026；3. 华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

随着城市轨道交通的高速化，列车运行的舒适性及安全性有了更高的要求，轨道结构应具有高平顺性、高稳定性。线路运营一段时间后，轨道几何状态会发生改变，为保证轨道的平顺性应进行定期检测[1]。轨道几何状态检测方法有静态检测和动态检测两种，静态检测是利用人工或轨检小车在无轮载作用下的轨道质量检测，动态检测是利用轨检车在列车车轮荷载作用下对轨道质量的快速检测[2]。轨道动态不平顺对列车安全、车辆振动及轮轨相互作用力产生重要影响，因此，目前轨道质量评估中主要采用轨检车检测动态不平顺评价轨道平顺状态[3]，然而，车辆运行时会导致轨道结构发生动态变形，从而影响动态不平顺的检测结果。

郭宇等[4]通过建立无砟轨道—路基力学模型，研究了不同形式的路基沉降与轨面变形间的映射关系。蔡小培等[5]针对高铁板式无砟轨道结构，分析了地面沉降对轨道平顺性的影响规律。陈兆玮等[6-8]研究了桥墩沉降引起轨道不平顺对行车的影响。以上主要对轨道下部结构的变形、沉降等引起的静态不平顺进行研究，然而，现有研究缺乏轨道结构敏感因素对高低不平顺的影响分析。

本文通过多体动力学软件 Universal Mechanical建立车辆—轨道动力学模型，基于惯性基准法原理计算轨道高低不平顺。分析轨道结构振动及扣件垂向刚度、路基支承刚度、轨枕间距对中长波高低不平顺的影响及变化规律。

1 惯性基准法估算轨道高低不平顺

1.1 惯性基准法原理

目前，世界各国用来测量高低不平顺的方法可归纳为弦测法和惯性基准法两大类[3]。弦测法有夸大、缩小、不能反映出实际不平顺的正负方向等严重缺陷，由于惯性基准法解决了“振动质量法”和“轴箱加速度积分法”不能满足需测波长范围要求等问题，克服了弦测法的严重缺陷，能够如实反映实际轨道不平顺，因此，各国铁路部门主要采用惯性基准法测量轨道不平顺。本文估算轨道高低不平顺也采用惯性基准法，当车轮与钢轨保持相互接触时，车轮轴箱的垂向位移H即为轨道高低不平顺η，等于车体垂向位移Z和车体与轴箱间的相对位移W之和；车体相对于惯性基准线位移Z通过加速度传感器测出车体垂向加速度对其进行二次积分所得；车体与轴箱间的相对位移W，可通过车体与轴箱相对惯性基准线的位移得出。

提取Z和W数据结果之后，则可通过公式(1)计算得到轨道高低不平顺η[9]。

1.2 车辆模型

通过多体动力学软件UM建立车辆模型，该车辆模型由一个车体和两个转向架子系统组成，其中转向架子系统由一个构架、两个轮对和4个轴箱构成，构架与轮对之间有一系悬挂，车体和构架之间有二系悬挂。轮对与轴箱之间通过铰连接，轴箱与构架之间通过弹簧力元、减振器连接。车辆模型部分参数如表1所示，UM中建立的转向架及6辆编组B型车如图1所示。

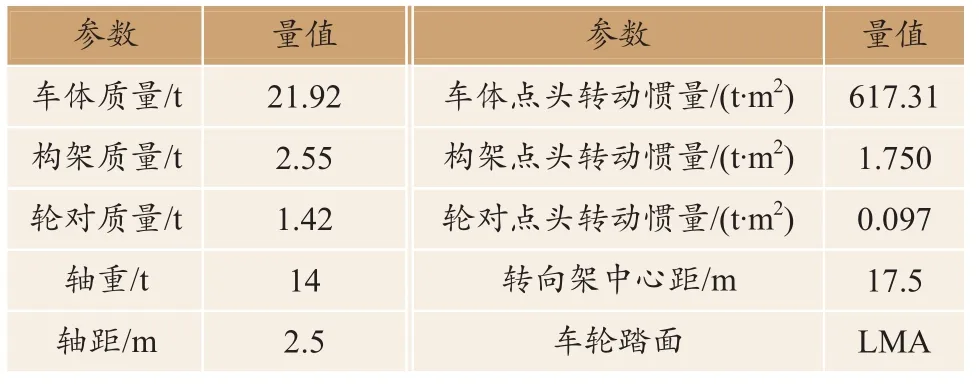
表1 车辆系统参数Table 1 Vehicle system parameters

图1 车辆模型Figure 1 Vehicle model

1.3 高低不平顺计算方法的验证

无质量轨道是将轨道视为无质量的力元，可用于优化和检验所建立模型的正确性，仿真检测高低不平顺流程如图2所示。选用德国低干扰谱离散傅里叶变换后的1 km高低不平顺样本作为激励，通过不平顺样本与无质量轨道仿真计算出的不平顺作对比可以验证估算方法的正确性，不平顺样本如图3所示，波长范围为2～100 m。

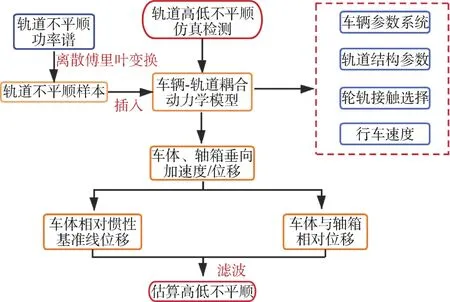
图2 估算高低不平顺流程Figure 2 Estimating longitudinal irregularity process

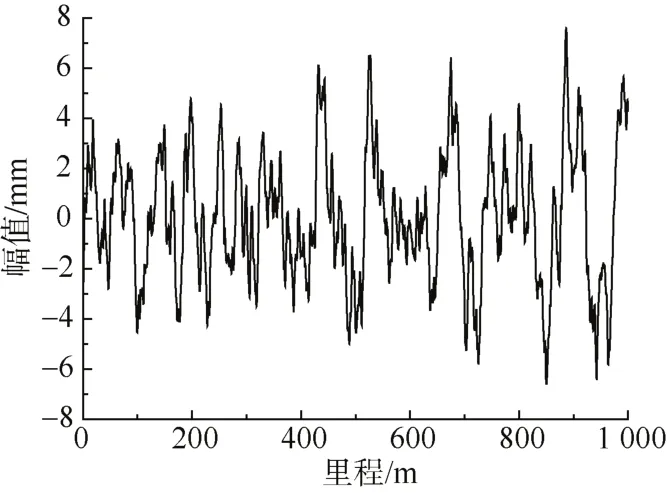
图3 1 km高低不平顺样本Figure 3 1 km longitudinal irregularity sample

将高低不平顺样本作为外部激励，导入UM中建立的车辆—无质量轨道耦合模型进行动力学分析，计算轴箱和车体底部对应轴箱位置处的加速度、位移，计算结果如图4所示。

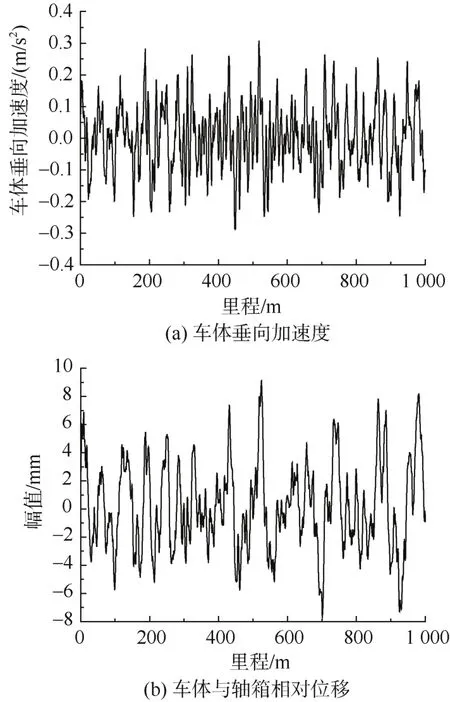
图4 动力学计算结果Figure 4 Dynamic calculation results

根据惯性基准法原理，由式(1)得出高低不平顺估算值，将估算不平顺与样本的幅值、轨道谱进行对比，如图5所示。分析图5(a)可知，估算不平顺与样本的波形、幅值基本重合，两者幅值差最大值为0.164 mm；分析图5(b)可知，从频谱角度分析时两者轨道谱几乎一致。因此，惯性基准法估算高低不平顺的方法较好，计算精度较高。

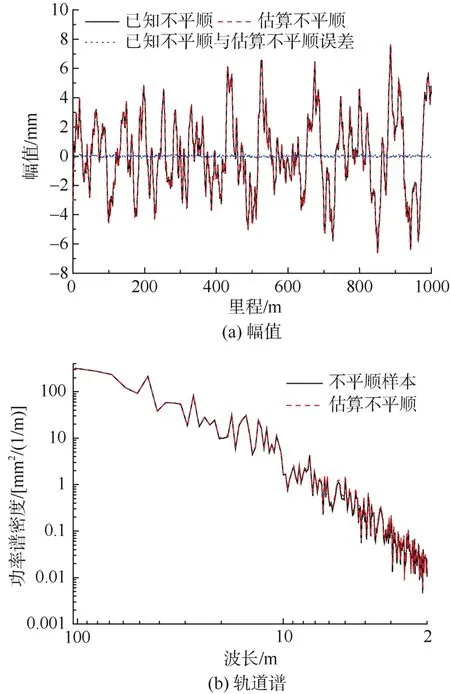
图5 不平顺样本与估算不平顺对比Figure 5 Comparison between irregularity sample and estimated irregularity

2 轨道结构振动对高低不平顺的影响

2.1 柔性轨道模型

在软件UM中，柔性轨道模型将钢轨视为Timoshenko梁，扣件模拟为Bushing力元，轨枕模拟为刚体，模型如图6所示，结构主要参数如表2所示。

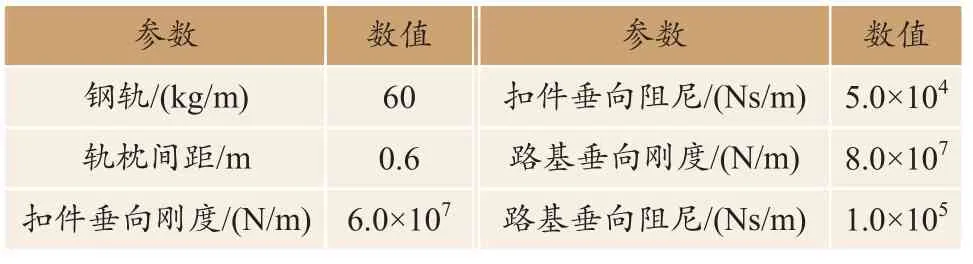
表2 柔性轨道结构参数Table 2 Structural parameters of flexible track

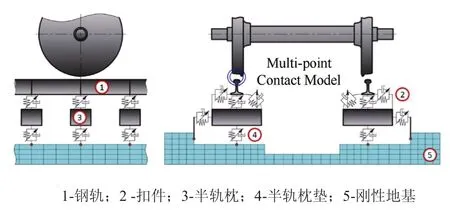
图6 半刚性轨枕柔性轨道模型Figure 6 Semi rigid sleeper flexible track model

2.2 无质量轨道与柔性轨道对比

为探究轨道结构振动对动态高低不平顺的影响，建立车辆—无质量轨道、车辆—柔性轨道耦合模型，在已知1 km不平顺样本激励的情况下，计算无质量轨道、柔性轨道高低不平顺，计算结果如图7所示。

分析图7可知，柔性轨道与无质量轨道高低不平顺波形相似，幅值上差异不明显。为更直观地分析两种不平顺在幅值上的差异，每200 m数据为一段求幅值差最大值，对比结果如表3所示。

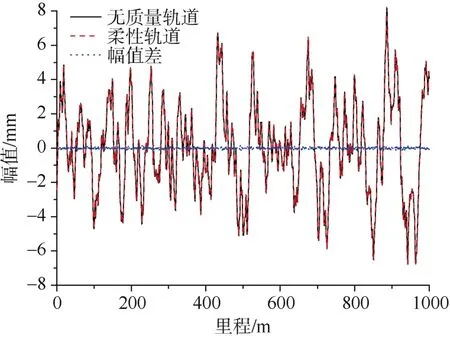
图7 无质量与柔性轨道估算不平顺对比Figure 7 Comparison of estimated irregularity between massless track and flexible track

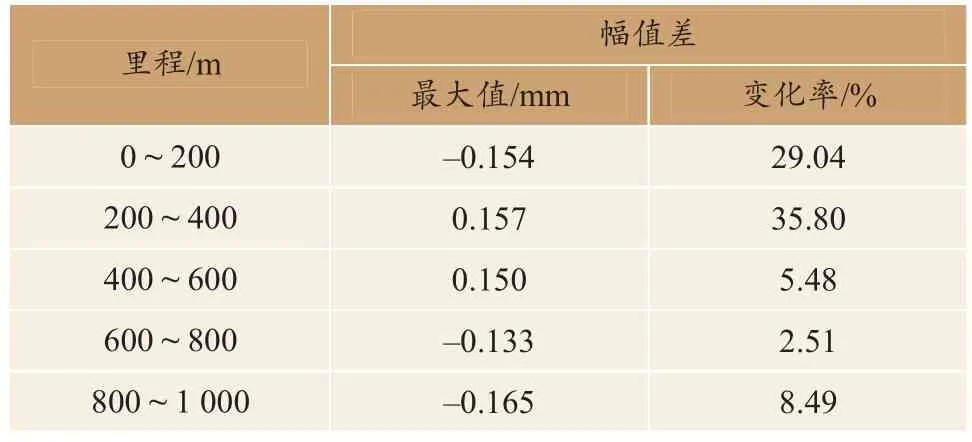
表3 柔性轨道与无质量轨道不平顺幅值差对比Table 3 Comparison of irregularity amplitude differences between flexible track and massless track

由表3可知，柔性轨道与无质量轨道不平顺幅值差最大值为0.157 mm，最大变化率为35.80%。由此得出，柔性轨道模型估算得出的高低不平顺大于无质量轨道模型，其原因为无质量轨道下部结构较简化，钢轨采用力元直接支承，而柔性轨道的钢轨下部有半轨枕及刚性地基支承，后者荷载传递性更好且能真实反映轨道平顺性。为分析轨道结构振动对不同波长范围内高低不平顺的影响，计算了两种轨道模型下的轨道谱，如图8所示。

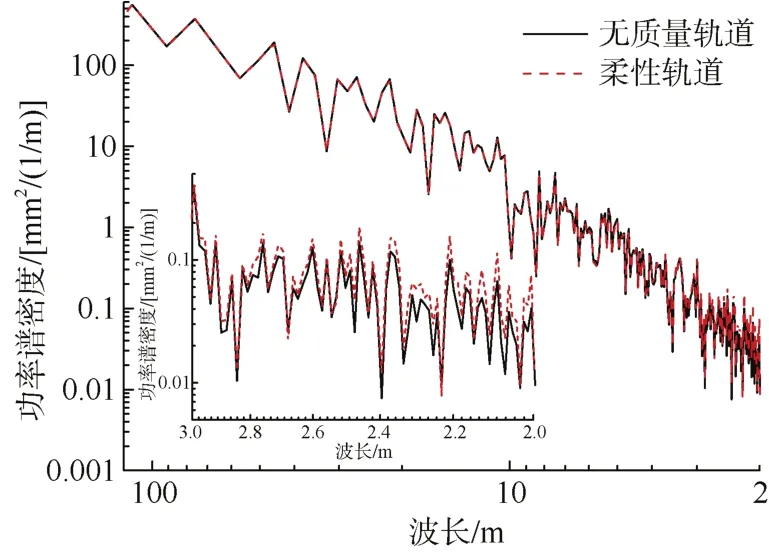
图8 无质量轨道与柔性轨道的轨道谱对比Figure 8 Comparison of track spectra between massless track and flexible track

图8从轨道谱的角度分析了无质量轨道与柔性轨道动态高低不平顺的差异，在波长6～120 m范围内，无质量轨道与柔性轨道的轨道谱相近，柔性轨道稍小于无质量轨道的轨道谱；在波长2～6 m范围内，柔性轨道轨道谱明显大于无质量轨道谱，即表明轨道结构振动对高低不平顺具有一定影响，且主要影响波长2～6 m范围内的高低不平顺。

3 结构敏感参数对高低不平顺的影响

线路在长期运营过程中，轨道结构部件老化会引起轨道结构参数改变；另一方面，不同的线路，其轨道结构参数设计也不同，结构参数的不同对高低不平顺发展趋势的影响有所不同。本文分析了扣件垂向刚度、路基支承刚度、轨枕间距对高低不平顺的影响。

3.1 扣件垂向刚度的影响

在轨道结构中，扣件系统的作用是连接钢轨与轨枕，并提供轨道系统弹性的主要部件[10]。当线路运营一段时间后，扣件会发生松动或脱落，从而导致扣件刚度发生变化[11]。本文设置了3种扣件垂向刚度工况。工况1：3.0×107N/m；工况2：6.0×107N/m；工况3：9.0×107N/m，3种工况计算得出的高低不平顺如图9所示。

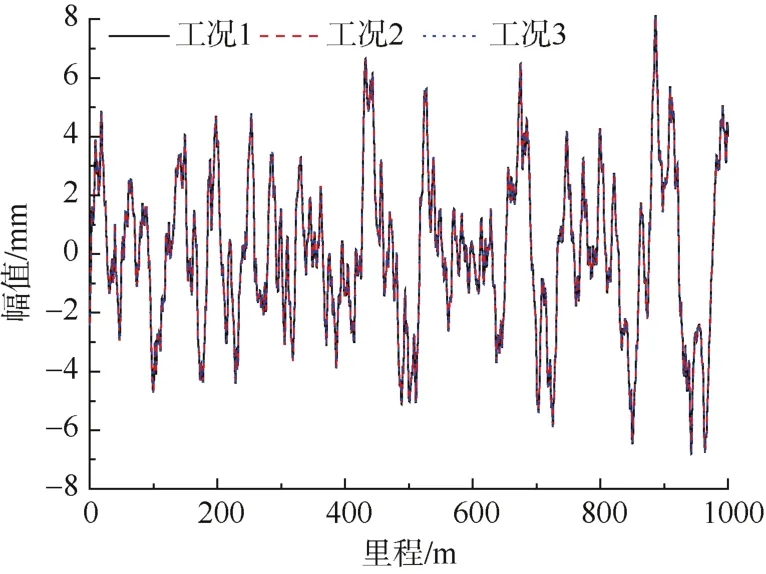
图9 不同扣件刚度下高低不平顺对比Figure 9 Comparison of longitudinal irregularity under different fastener stiffness

图9从幅值角度分析了3种扣件垂向刚度工况下的轨道动态高低不平顺。由图9可知，3种工况下轨道不平顺波形相似，幅值差异不明显。为了更直观地分析3种工况下高低不平顺的差异，文中以工况1为基准，计算了 3种工况下高低不平顺的幅值差，如表4所示。

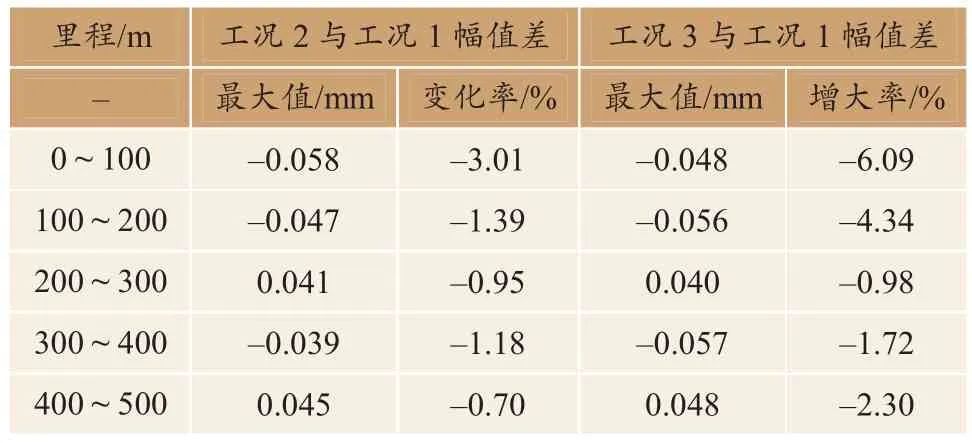
表4 不同扣件刚度下不平顺幅值差对比Table 4 Comparison of irregularity amplitude difference under different fastener stiffness

分析表4可知，工况2与工况1不平顺幅值差最大变化率为-3.01%，工况3与工况1不平顺幅值差最大变化率为-6.09%，即轨道高低不平顺随扣件垂向刚度的增大而减小，但幅值变化较小。为了分析扣件刚度在不同波长成分范围内对高低不平顺的影响，计算了轨道谱，如图10所示。

图10从轨道谱角度分析了3种工况的轨道高低不平顺，在波长4～120 m范围内，3种工况轨道谱相近；在波长2～4 m范围内，可以较为明显地看出轨道谱随着扣件垂向刚度的增大而减小。

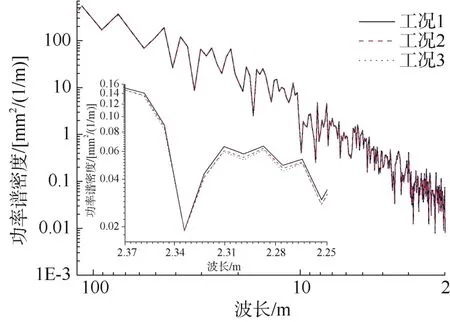
图10 不同扣件刚度下轨道谱对比Figure 10 Comparison of track spectra under different fastener stiffness

综上可知，扣件垂向刚度对高低不平顺幅值的影响较小，而从轨道谱角度分析时，在波长2～4 m范围内，高低不平顺随着扣件垂向刚度的增大而减小。其原因为长波不平顺幅值大，中波幅值小，由于中波的幅值变化被长波覆盖，导致从幅值角度无法准确分析扣件的影响。因此，应结合幅值与轨道谱分析结构敏感参数对不平顺的影响。

3.2 路基支承刚度的影响

路基承受列车运行的动荷载及轨道结构的静荷载，并将承受的荷载传递至地基深处。路基受到自然因素影响及列车在长期荷载运营下，路基刚度会发生改变。本文设置了3种路基支承刚度工况。工况1：4.0×107N/m；工况2：8.0×107N/m；工况3：1.2×108N/m。3种工况下轨道高低不平顺对比分析结果如图 11、表5所示，轨道谱对比结果如图12所示。

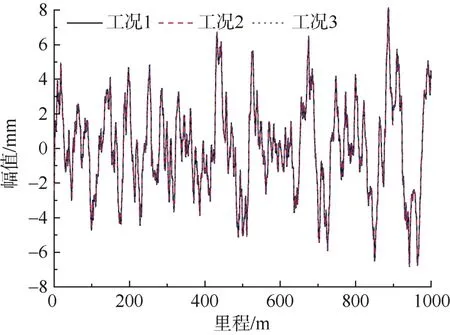
图11 不同路基支承刚度下高低不平顺对比Figure 11 Comparison of longitudinal irregularity under different subgrade support stiffness

分析图11和表5可知，工况2与工况1高低不平顺幅值差最大变化率为-8.44%，工况3与工况1高低不平顺幅值差最大变化率为-12.96%，即轨道高低不平顺随路基支承刚度的增大而减小。

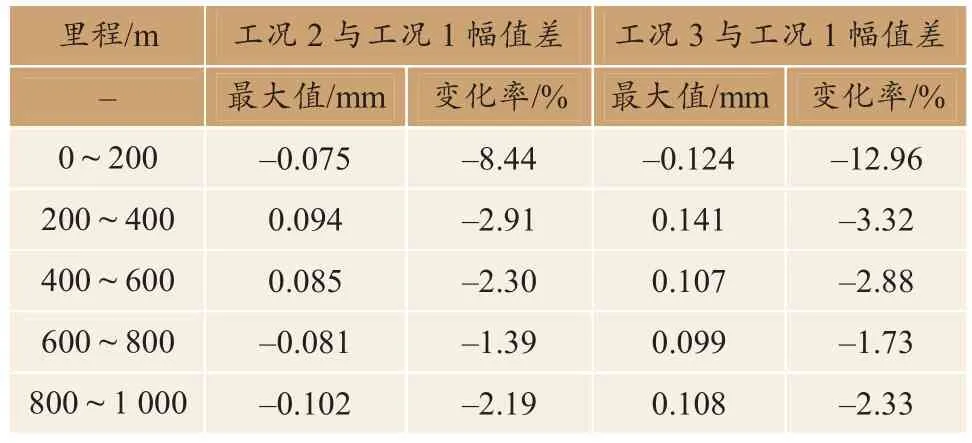
表5 不同路基支承刚度下不平顺幅值差对比Table 5 Comparison of irregularity amplitude difference under different subgrade support stiffness

分析图12可知，在波长10～120 m，3种工况轨道谱相近；在波长2～10 m范围内，轨道谱变化较为明显且随路基支承刚度的增大而减小。由此表明，路基支承刚度对动态高低不平顺具有一定影响，且主要影响波长2～10 m。

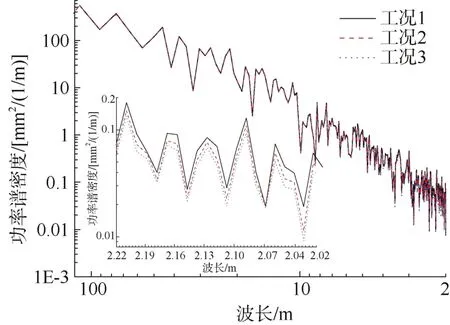
图12 不同路基支承刚度下轨道谱对比Figure 12 Comparison of track spectra under different subgrade support stiffness

3.3 轨枕间距的影响

轨枕间距作为轨道结构的重要参数，不同的轨枕间距会造成不同的轨道结构刚度不平顺，对车辆—轨道系统具有不同的动力响应。本文设置了3种轨枕间距工况。工况1：0.6 m；工况2：0.625 m；工况3：0.65 m。3种工况下轨道高低不平顺分析对比结果如图13、表6所示，轨道谱对比结果如图14所示。

分析图13、表6可知，工况2与工况1不平顺幅值差最大变化率为4.57%，工况3与工1不平顺幅值差最大变化率为 8.59%，即轨道高低不平顺随轨枕间距的增大而增大，幅值总体上存在较大的变化。

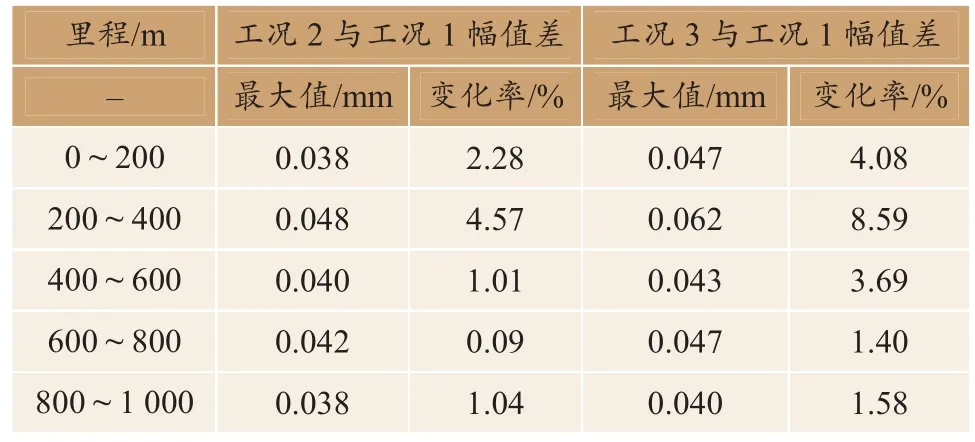
表6 不同轨枕间距下不平顺幅值差对比Table 6 Comparison of irregularity amplitude difference under different sleeper spacing

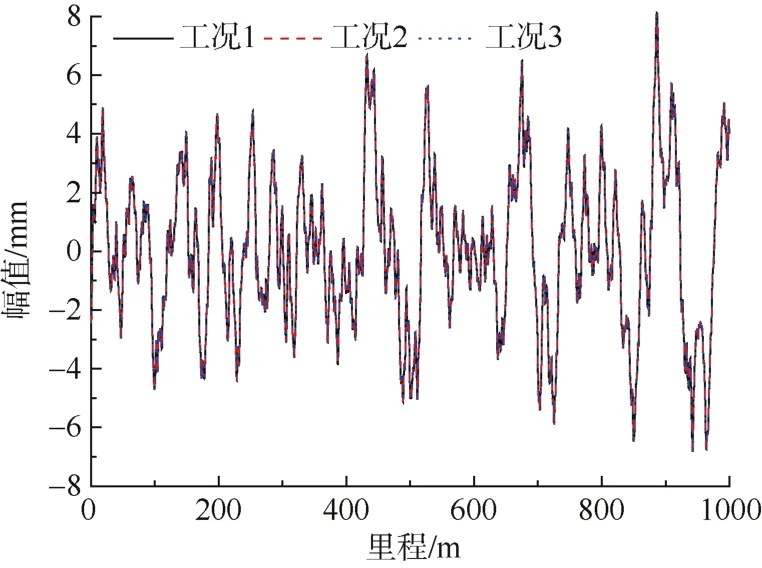
图13 不同轨枕间距下高低不平顺对比Figure 13 Comparison of longitudinal irregularity under different sleeper spacing

分析图14可知，在波长3～120 m范围内，3种工况轨道谱相近；在波长2～3 m范围内，可以明显看出轨道谱随轨枕间距的增大而增大。轨道高低不平顺随轨枕间距增大的原因为：随着轨枕间距的增大同一路段的轨枕数会减少，与此同时，共同承受车辆荷载的轨枕数减少，进而每根轨枕承受的荷载加大、行车平稳性降低、动荷载增大，最终导致轨道高低不平顺增大。

图14 不同轨枕间距下轨道谱对比Figure 14 Comparison of track spectra under different sleeper spacing

4 结语

本文通过多体动力学软件UM建立车辆—轨道耦合动力学模型，基于惯性基准法估算轨道高低不平顺，分析了轨道结构振动及扣件系统垂向刚度、路基支承刚度、轨枕间距等敏感因素对高低不平顺的影响，主要结论如下：

1) 柔性轨道与无质量轨道高低不平顺幅值差最大值为0.157 mm，最大变化率为35.80%；在波长2～6 m范围内，柔性轨道轨道谱明显大于无质量轨道，即表明轨道结构振动对高低不平顺有一定影响，且主要影响波长2～6 m。

2) 轨道高低不平顺随扣件垂向刚度和路基支承刚度的增大而减小，主要影响的波长范围分别为 2～4 m和2～10 m。

3) 轨道高低不平顺随轨枕间距的增大而增大，且在波长2～3 m范围内发展变化趋势较明显。

综上，轨道结构敏感参数对高低不平顺幅值的影响相对较小，而从轨道谱角度可得出不同波长成分的变化规律，波长小于6 m范围内的高低不平顺随敏感参数的改变而显著变化。因此，分析轨道高低不平顺的分布特征及其发展变化规律时，应结合幅值角度和轨道谱角度综合分析。