基于机器学习的地铁盾构隧道长期沉降预测

张研沁，狄宏规，徐永刚

（1. 同济大学道路与交通工程教育部重点实验室，上海 200092；2. 宁波市轨道交通集团有限公司，浙江宁波 315100）

1 研究背景

我国长三角地区地铁线网规模大，软土隧道沉降问题突出[1-2]，如上海地铁1 号线运营5 年后最大隧道累积沉降量超过200 mm[3]。过大的隧道沉降易造成结构病害，如管片接缝张开与错台、开裂、衬砌渗漏水、轨面变形超限等[4]。这不仅会增加养护维修成本，还会影响地铁线路结构和运营安全，因此如何进行沉降控制和治理，是备受关注和亟待解决的问题。例如，上海、宁波、南京等城市均尝试采用隧道底部注浆抬升或注浆加固稳定的方法，对发生沉降的隧道进行治理[5-6]。但是，由于运营期施工空间和天窗时间有限，采用注浆进行沉降控制和治理相对困难且不经济。因此，若能在设计阶段进行沉降预测或预处理，设计将更为有效。

导致隧道沉降的原因有很多，如软弱地层、列车荷载作用、渗漏水、周边开发等。不少学者分别研究和分析了列车循环荷载、周边开发、隧道渗漏水、结构形式[7-10]等单因素对隧道沉降的影响，然而长期沉降是由多因素耦合作用而引起的，因素难以剥离，单因素分析难以预测长期总沉降。现有的多因素分析方法(如智能算法)能够预测隧道的长期沉降[11-13]，考虑地铁沉降的主要原因[14]，但这类方法必须依赖所研究地铁隧道的前期沉降数据，在地铁设计阶段没有该线路隧道前期沉降数据的情况下，往往不具备可行性。因此，现阶段仍缺乏一个在设计阶段实现、反映多因素耦合作用且具有一定准确度的地铁盾构隧道长期沉降预测模型。

笔者基于机器学习方法，建立了一个依托区域地质信息和既有地铁隧道的沉降资料，预测相似地区同类型线路长期沉降的预测模型。利用主成分分析(PCA)，寻找沉降的主要影响因素以及缩减数据维度，比选5 种监督学习算法在模型中的预测效果，并对较优算法进一步调参，以南京地铁2 号线为例进行算例分析，可为地铁盾构隧道的沉降预控提供一种新思路。

2 预测模型

建立基于机器学习的地铁盾构隧道长期沉降预测模型的具体流程如图1 所示，模型共包含原始数据集构造与预处理、监督学习算法比选、带交叉验证的网格搜索三大主要部分。数据集构造与预处理是为了得到更适合训练的数据，监督学习算法比选与带交叉验证的网格搜索则是为了提高预测准确度。

2.1 数据集与数据预处理

监督学习是最常见、最成功的机器学习类型，其中的输入数据集是一个实例集，并以此得到输出。每条实例相当于统计学中的样本，其中元素包括标签和属性，如图2 所示。标签是机器学习的目标真值(即监督)，属性则是影响标签的各项因素。

本研究的数据集标签为沉降，属性为各影响因素，如土层性质及隧道空间位置、地下水位变化、列车

图1 建立沉降预测模型的流程 Figure 1 Flow chart of the settlement prediction model

图2 数据集示意 Figure 2 Schematic of the dataset

振动荷载等。其中，土层性质由土层参数和土层厚度数组表示，隧道空间位置由上覆土层、隧道层、下卧土层区分，地下水位由长期地表高程间接反映，列车振动荷载通过由列车时刻表计算的车速表征。由于数据资料限制，隧道渗漏水状态、周边施工等暂未考虑。

综上分析，每条实例可表示为

式中：Sl为实例l 数组；sl表示实例l 某年后的沉降量；Cil表示实例l 第i 层土的土层参数；hil表示实例l 第i层的土厚度；Gl表示实例l 的地面高程；vl表示实例l的车速。

需要指出的是，Cil中的土层参数结合地勘报告的数据，可选取含水量w、重度γ、孔隙比e、塑性指数IP、液性指数IL、压缩系数a、压缩模量Es、黏聚力c、内摩擦角φ、静止侧压力系数K0等。经过相关性分析和土力学知识证明，选取内摩擦角、液性指数、孔隙比作为土层参数表征，这是一个三维数组，有

式中：ei为第i 层土孔隙比；ILi为第i 层土液性指数；φi为第i 层土内摩擦角。

此外，由于软土地区地质剖面图中的土层一般不超过15 层，取上覆土1～7 层、隧道层、下卧土1～7层进行分析，即包含15×3 个土的参数、15 个土层厚度、1 个地面高程、1 个车速共62 个属性。由于监督学习的标签要求为沉降真值，因此样本数量m 取决于沿线沉降量测点数，工程上一般每20 m 设置一个测点。

为使测试结果有效地反映全线范围内沉降预测的有效性，将数据集按照里程段分为多份(保证在全线范围内均匀)，并在每一段内随机抽取10%的测点组成测试集(保证测试数据的选取随机)，其余部分组成训练集。为了消除各属性量纲的影响，先对n 个属性按列进行归一化，得到的数据分布特性不变，数据大小介于0～1 之间。测试集的数据在建模期间默认为未知，因此归一化操作仅在训练集中进行，之后再对测试集做与训练集同样的缩放。另外，由于数据集维数较高，因此笔者采用主成分分析法进行数据降维降噪。

2.2 监督学习算法的比选

针对该模型的沉降预测效果，对以下5 种监督学习算法进行比选：k 邻近算法、线性回归、决策树回归、核支持向量机、人工神经网络。k 邻近算法适用于小型数据集，在数据量不大的情况下可能会得到更好的结果；线性回归适用于庞大的数据集和高维数据，在数据足够丰富的情况下忽略非线性关系，能得到更加直观的结果；决策树可以可视化，并且可以创造精度更高的集成算法模型(如随机森林或梯度提升树等)，对数据预处理要求较低；核支持向量机通过参数的调整能够逼近任意函数，很适合中等大小的数据；人工神经网络通过隐藏层层数和节点数的调整，能够达到极高的精确度，尤其适合庞大的数据集，并能够通过联网条件进行实时更新学习。

利用不同监督学习算法构造的模型在测试集上复出的分数，比选出最适合沉降预测模型的监督学习算法，如图3 所示。

2.3 交叉验证与网格搜索

交叉验证是一种评估泛化能力的统计学方法，将数据集多次划分、学习、测试，并以测试集分数的均值反映整体泛化能力。网格搜索则是调参以提高泛化能力的典型方法，将每种参数取值组合下的测试集分数进行比选，得到泛化能力最高的参数取值组合。将两者结合到一起，用交叉验证来评估每种参数组合的性能，过程如图4 所示。

图3 监督学习算法比选 Figure 3 supervised learning algorithm selection

图4 带交叉验证的网格搜索 Figure 4 Grid search with cross-validation

3 算例分析

数据来源于南京地铁2 号线汉油段地勘报告、地质剖面图以及长期沉降监测数据。线路自2010 年运营以来，资料保存完备，加之南京地区软土分布广泛，对于软土区域盾构隧道的长期沉降研究具有一定代表性，因此选取其进行算例分析。

图5、6 分别为南京地铁2 号线汉油段的地质剖面图和该区段运营9 年后的沉降曲线。将剖面图转化为各点的土层厚度、地面高程、隧道埋深等属性，将沉降作为标签分别输入数据集。由于上、下行线路沉降趋势相同，故本研究采用来自上行线路的共447 条数据。

图5 算例地质剖面图 Figure 5 Geologic profile of the case

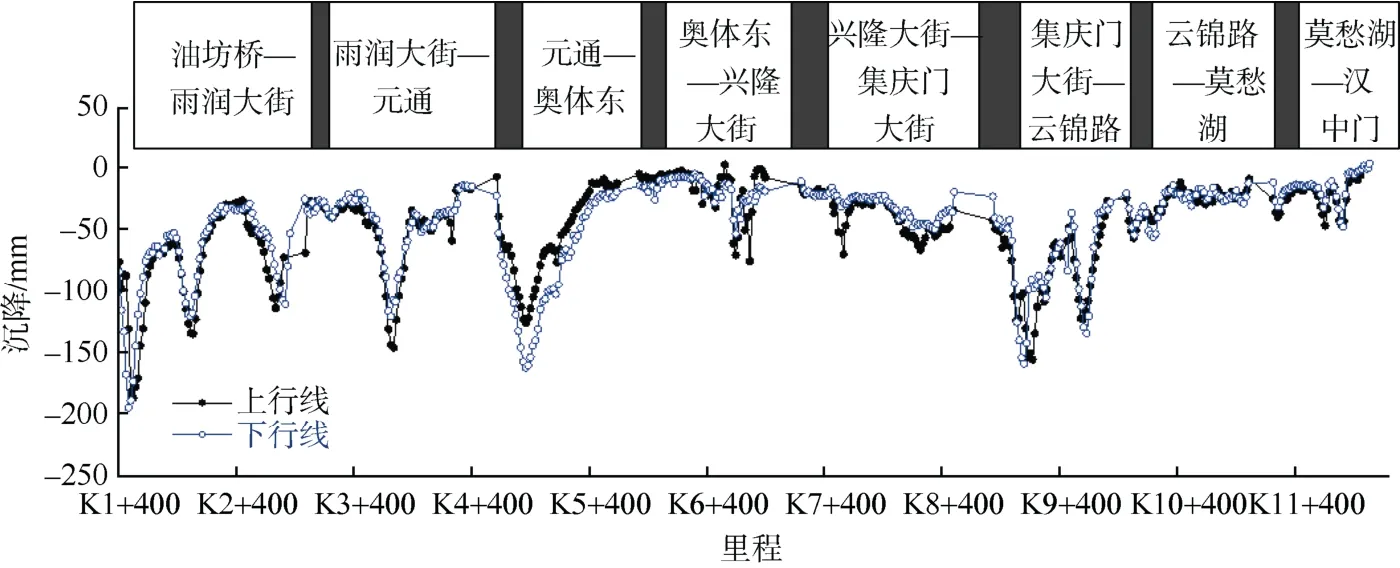
3.1 隧道沉降的主成分分析

该算例58 个属性(4 个0 列舍去)经过主成分分析(PCA)后，数学变换为对标签贡献值逐渐减小的58 个主成分，其前21 个贡献值之和已超过95%，故将余下的成分视为噪声舍去，达到降低维数的目的，以方便后续模型的运算。

在21 个保留的主成分中，58 个属性的重要程度热力图如图7 所示，红色、蓝色分别表示正、负相关，颜色越深表示因素越重要。由此，将因素划分成模糊段1、清晰段1、模糊段2、清晰段2 四部分。可以看出，影响隧道长期沉降的主要因素为隧道层附近几层软土的性质(清晰段1)以及列车车速(清晰段2)。

3.2 监督学习算法的比选结果

采用不同监督学习算法的模型，在训练集、测试集上的分数如表1 所示。该分数来自两个数据集中预测值和标签值的预测分数(回归值R2)，越接近1 代表预测越准确。显然，有标签提示的训练集分数高于没有标签 提示的测试集。

图7 重要程度热力图 Figure 7 Attributes’ importance heat map

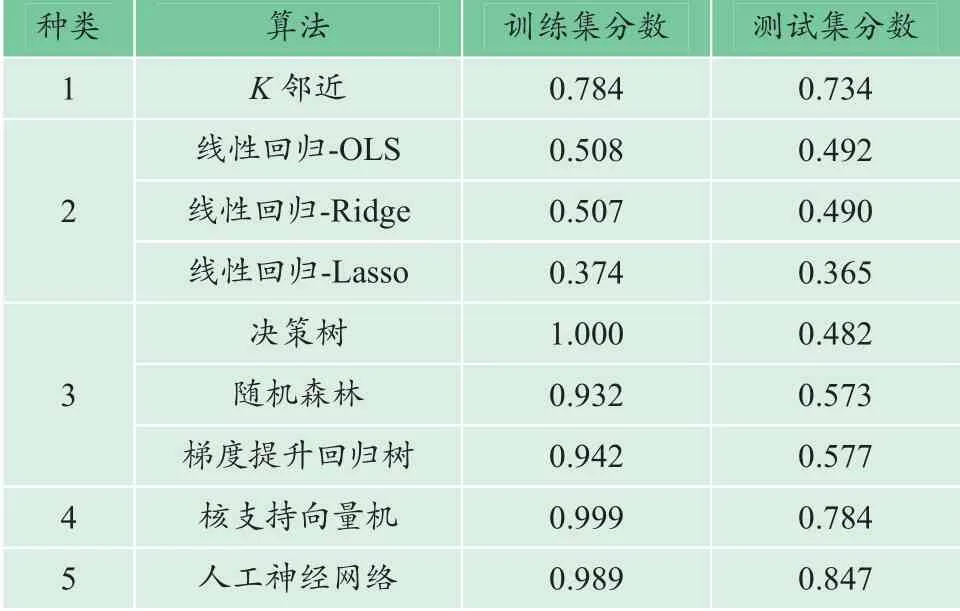
表1 监督学习算法比选 Table 1 Supervised learning algorithm comparison

3.3 带交叉验证的网格搜索结果

从表1 结果来看：K 邻近在默认参数时，训练集和测试集分数接近，说明不调参的结果数据就已较好；线性回归在测试集和训练集上的分数都很低，所以不考虑该方法；决策树类在训练集上分数高而测试集上分数低，出现明显的过拟合问题，所以需要调参；经验表明，核支持向量机和人工神经网络均十分依赖参数设置，因此需要调参。

对此，根据各算法函数中的参数对结果的影响和可取值的范围，设置参数网格如表2 所示。分别采用带交叉验证的网格搜索进行枚举计算，以确定最高交叉验证平均分值的参数组合。

不同参数组合下的预测分数热力图分别如图8(a)～(c)所示。对决策树算法影响较大的两个参数为最大树深max_depth 和最大特征数max_features，它们在最优组合下经过10 折交叉验证，训练集平均分数能够达到0.69。同样地，对核支持向量机算法影响较大的两个参数为正则化参数C 和核宽度gamma，最优组合下经过10 折交叉验证，训练集分数能够达到0.8。经过网格搜索，人工神经网络采用lbfgs 决策函数和relu 激活函数，4 层隐藏层，alpha=10，且分数较高；隐藏层结构为[40，60，60，50]时经过10 折交叉验证，训练集的平均分数最高，能达到0.82。

表2 参数网格 Table 2 Parameter grid

综上所述，采用人工神经网络及对应参数，在本算例中，最终预测模型的沉降量预测值与真实值的预测分数为0.86，如图9 所示。如前所述，测试集和训练集沿里程段均匀划分，随即均匀分布，代表全线沉降数据，45 条(10%)测试集数据的里程随机均匀分布于多个里程段内，在学习过程中不输入沉降标签，可以将其视作相同地铁在类似地质区域修建而沉降未知的

图8 预测分数热力图 Figure 8 Scores heat map

图9 模型预测结果 Figure 9 Model prediction results

情况。因此，对于没有沉降标签监督的数据，能够预测其沉降，证明了在未知沉降量的情况下预测长期沉降的可能性；沉降预测准确度达到0.86，说明模型预测结果具有一定的可靠性。特别注意的是，个别误差较大的点可能是由于未考虑周边施工影响的不确定因素造成的。

4 结语

1) 本研究基于机器学习方法，建立了盾构隧道长期沉降模型。该模型能筛选主要影响因素，并寻找最佳算法和最优参数，对模型的泛化能力给予评价。该模型的算例验证了在新建地质情况明确的同类型地铁中，能够预测该新建地铁的长期沉降，结果较为准确，为地铁沉降预控提供新思路。在今后工程大数据的支持下，通过拓展数据集加强学习，该模型的适用性和准确度还可能进一步提高。

2) 在监督学习算法中，核支持向量机算法与人工神经网络算法对于该模型都能达到较高的精度，然而其对参数的依赖性很高，需要细致地调参才能提高预测精度。

3) 以人工神经网络算法作为监督学习算法，调参后得到最终预测模型的预测准确度为0.86，10 倍交叉验证的平均准确度为0.82；个别点的预测值与真值存在一定误差，推测是由于预测模型中未考虑周边施工影响等不确定因素而造成的。