水平地震作用下T 型换乘地铁车站结构变形分析

李 霞 ，鲁卫东

（1. 北京城建设计发展集团股份有限公司，北京 100037； 2. 城市轨道交通绿色与安全建造技术国家工程实验室，北京 100037）

1 研究背景

在我国特大一线城市中，地铁系统在城市地下四通八达，其建设规模和运行速度均已超过了很多发达国家，且这些地铁的地下结构大都没有经过大地震的考验。地铁的地下结构是否经得起大震的考验，已经成为影响城市安全的重要因素，也越来越得到人们的重视。1995 年，在日本阪神地震中，神户市地铁车站的结构遭到严重破坏，清楚地表明地层会发生较大的变形和位移，地铁等地下结构可能会出现严重的损害，因此对其抗震问题应给予高度重视。换乘车站具有规模大、结构复杂、客流量大等特点，且在很多城市的地下轨道交通线网中设置有两线换乘车站、三线换乘车站，有些换乘车站与地上交通枢纽无缝连接，客流量极大，因此其抗震安全性更应当给予高度重视。

美国、日本等发达国家对地下结构的抗震性能研究起步较早，并提出了一些实用的抗震设计分析方法[1-9]。近十几年来，我国在该领域的研究力度逐步增加并掀起了热潮，积累了一定的成果，并相继出台了《城市轨道交通结构抗震设计规范》(GB50909—2014)[10]、《地下结构抗震设计标准》(GB/T51336—2018)[11]。换乘地铁车站的建设规模大、结构复杂、地震响应影响因素多，目前有关其地震反应的研究成果极少。张宇[12]研究了不同水平输入地震波和不同地层4 种情况下T 型交叉车站结构的损伤发展趋势，指出需要在整体考虑两线车站相互作用的基础上进行地铁结构设计。王国波等[13]开展了在水平横向地震作用下十字换乘地铁车站结构的地震响应研究，得到了其空间效应、整体抗震性能优于单体车站的结论。于仲洋等[14]通过对比水平地震作用下三维单层交叉换乘地铁车站及相对应的二维标准车站结构的内力，给出单层交叉换乘地铁车站中交叉部分的影响范围，并对影响范围内的结构采用改进的方法进行设计。马腾飞等[15]研究了水平地震作用下的交叉换乘地铁车站，发现新建车站对既有车站的变形有约束作用，在新建车站与已有车站的连接处有明显的应力集中。

鉴于此，笔者以南京某两条地铁线路T 型换乘车站为背景，采用动力时程分析方法，建立场地土-T 型换乘车站结构的三维动力分析模型，分别输入相互垂直的水平地震作用和竖向地震作用，系统研究不同地震作用下T 型换乘车站结构的地震响应，揭示T 型换乘车站结构的地震响应规律。因篇幅有限，下面着重分析相互垂直的两个水平方向分别输入地震作用时T 型换乘地铁车站结构的变形特点，揭示T 型换乘地铁车站结构在水平地震作用下的变形规律，为同类建设工程抗震设计变形验算选取层间位移差控制断面提供依据。

2 工程概况

2.1 换乘车站的结构概况

两地铁线T 型交叉换乘站的平面布置如图1 所示，两线车站均为地下箱型框架结构，车站均沿纵向设置纵梁，为梁柱受力体系，其中地铁1 线为三层三跨车站，地铁2 线为两层三跨车站，车站标准断面如图2所示。两线车站均采用明挖法施工，地下连续墙围护。

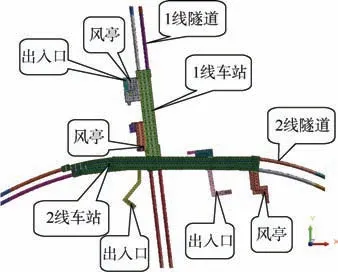
图1 T 型换乘车站平面布置 Figure 1 Layout plan of T-type transfer station

2.2 地质条件及土层参数

根据岩土工程勘查报告，场地土层自上而下主要有杂填土、淤泥质粉质黏土(夹粉砂)、粉质黏土(夹粉砂)、粉(细)砂、中(粗、砾)砂及卵砾石混合土、泥质砂岩等土层。场地工程的地质剖面如图3 所示，车站结构主要位于淤泥质粉质黏土层中，土层动力学参数如表1 所示。

2.3 场地类别和地震动参数

工程场地类别为Ⅱ类，设计地震动加速度反应谱特征周期Tg=0.45 s。抗震设防烈度为7 度，设计基本地震加速度值为0.10g，设计地震为第一组。抗震设防类别为乙类。

3 动力时程分析

采用midas GTS NX 进行三维建模，采用基于等效线性化的土-地下结构整体动力时程分析方法[16]，计算在E2 和E3 地震作用下换乘车站结构在两个水平方向的变形规律。

3.1 计算模型

土-T 型换乘车站结构的系统有限元模型的尺寸XYZ=440 m×550 m×70 m，模型顶面取至地表，底面取至基岩面，模型底面固定，侧边界采用自由场单元，考虑远场波传入和近场波传出时的辐射吸收作用[16]。土层简化为水平成层地层，土体采用四面体单元模拟。结构有限元网格如图4 所示，车站墙、板均采用板单元模拟，梁、柱采用梁单元模拟。

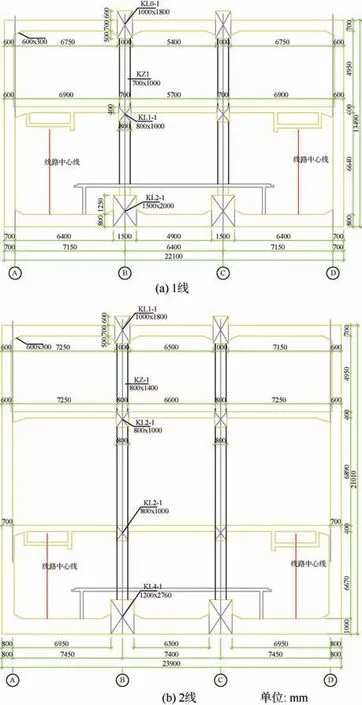
图2 T 型换乘站的标准断面 Figure 2 Standard section of T-type transfer station

图3 地质岩层分布 Figure 3 Geological section of the station

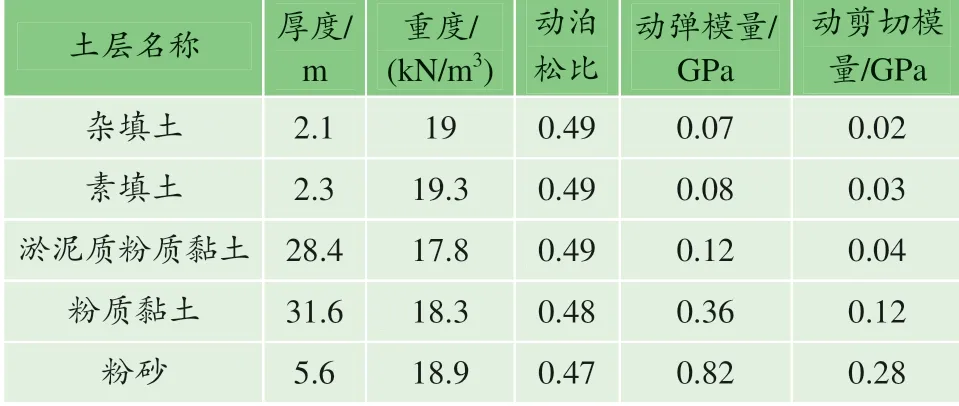
表1 土层动力学参数 Table 1 Soil dynamic parameters

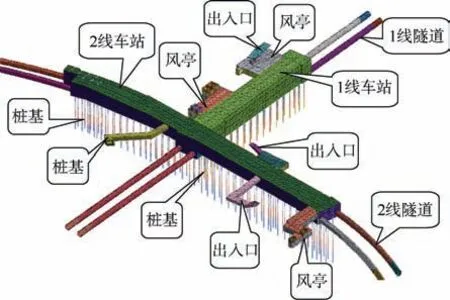
图4 T 型换乘车站的有限元网格 Figure 4 Finite element mesh diagram of T-type transfer station

模型边界采用自由场单元，自由场分析产生的作用力作为内力通过自由场单元传递到模型主区域，同时边界产生的反射波被自由场单元的吸收边界条件吸收，自由场单元如图5 所示[17]。本研究采用时域分析，土层阻尼采用Rayleigh 阻尼，即C=αM+βK，其中α、β 由下式[15]获得，即

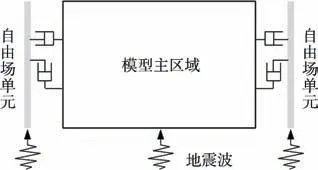
图5 自由场单元示意 Figure 5 Schematic diagram of free field unit

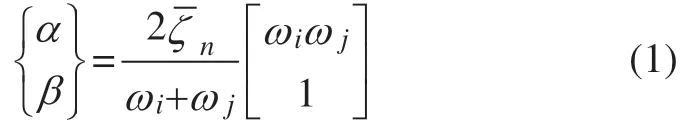
式中，ωi、ωj分别为土体的第一阶自振频率和地震波的卓越频率，ζn为土体的等效阻尼比。

3.2 地震作用

图6 E2 地震作用的时程曲线 Figure 6 E2 earthquake action time history curve

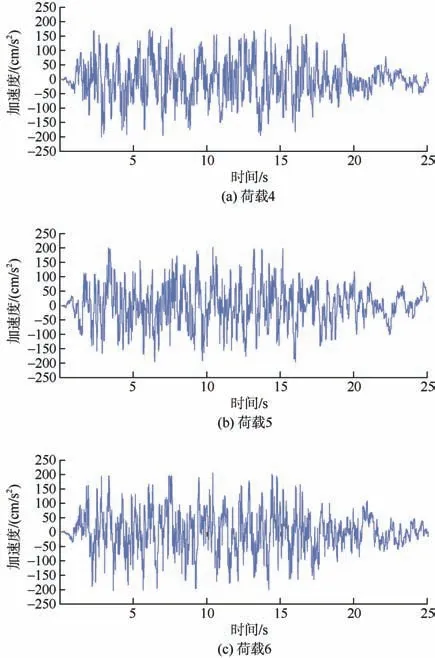
图7 E3 地震作用的时程曲线 Figure 7 E3 earthquake action time history curve

根据场地地震安全性评价报告，分别选取E2、E3地震作用的各3 条地震波，波形图分别如图6、7 所示。 因换乘车站的两线呈T 型交叉，且分别为地下3 层车站和地下2 层车站，为系统分析换乘车站结构的地震响应规律，拟定地震波的施加方向分别为垂直换乘车站两线车站的纵轴方向，如图8 所示，即分别沿X 轴、Y 轴方向输入6 组地震波，共12 个工况，分析工况如表2 所示。

图8 地震动的输入方向 Figure 8 Earthquake input direction

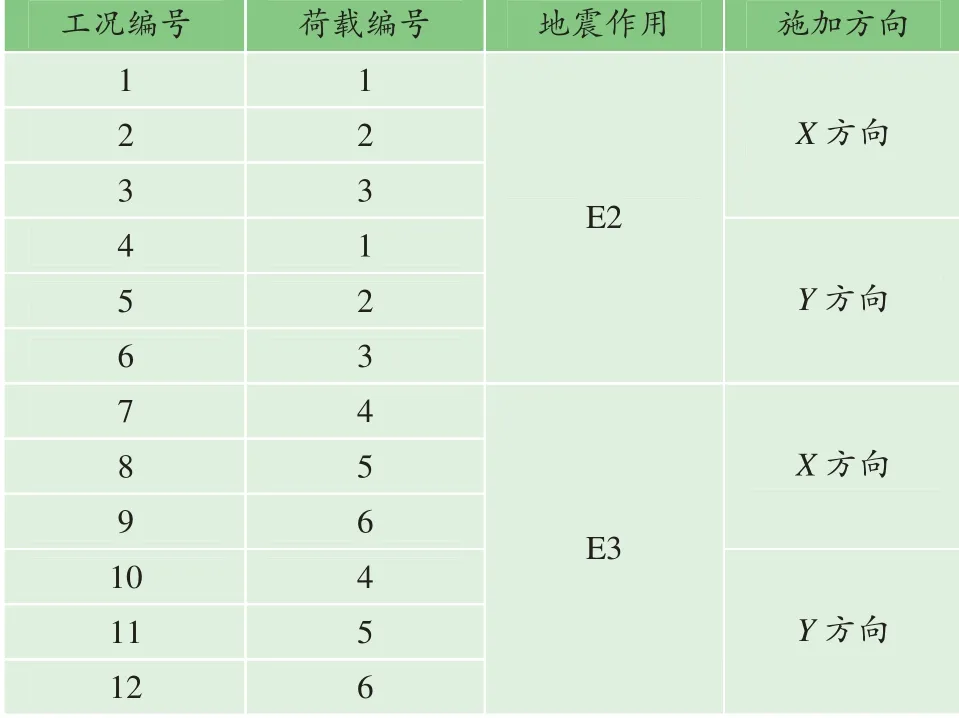
表2 分析工况 Table 2 Wor king conditions

3.3 结果分析

为全面系统地分析车站结构的地震响应，选取结构不同部位的7 个断面进行地震响应分析，其中1 线车站结构选取3 个断面，2 线车站结构选取4 个断面，选取断面的位置如图9 所示。

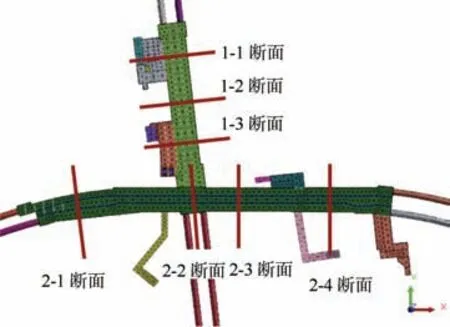
图9 断面布置 Figure 9 Sectional layout

3.3.1 E2 地震作用下结构变形分析

3.3.1.1 最大位移分析

在工况1～3 中，即在X 方向E2 地震荷载作用下，换乘车站结构沿X 方向水平位移的最大值分布云图如图10 所示。由图可知，换乘车站结构沿X 方向的水平位移随结构在土层中深度的减小而增大，最大值均发生在1 线车站主体结构的顶板部位，该部位沿1 线车站纵向，位于车站中部偏远离两线交叉部位处，最大值分别为48.72、47.26、46.29 mm；换乘车站结构沿X 方向水平位移的最小值位于两线车站的交叉部位。

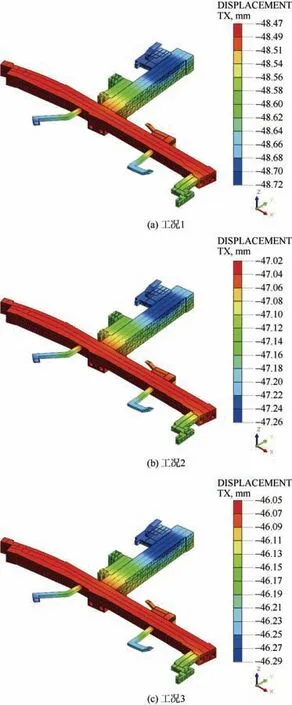
图10 X 方向位移的最大值 Figure 10 Maximum displacement in X direction

在工况4～6 中，即在Y 方向E2 地震荷载作用下，换乘车站结构沿Y 方向水平位移的最大值分布云图如图11 所示。由图可知，换乘车站结构沿Y 方向水平位移的最大值分别为48.76、47.30、46.32 mm，最大值均发生在2 线车站主体结构的顶板部位，该部位沿2线车站纵向，位于两线车站以两线车站交叉部位为分界的两部分中部偏远离两线交叉部位处；换乘车站结构沿Y 方向水平位移的最小值均位于两线车站的交叉部位。

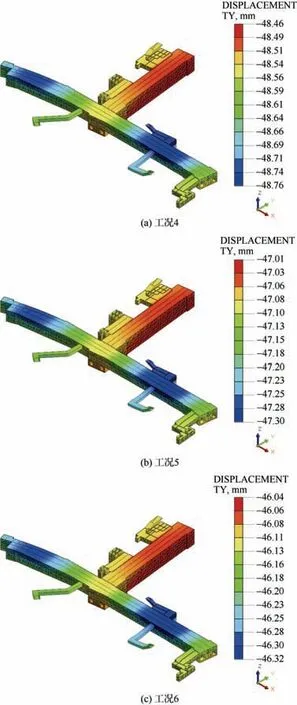
图11 Y 方向位移的最大值 Figure 11 Maximum displacement in Y direction

由以上分析可知，在E2 水平地震作用下，T 型换乘车站结构的水平位移随其在土层中深度的增大而减小；T 型换乘车站位移的最大部位出现在垂直于输入地震动方向的线路车站，沿该线路车站纵向位移的最大值位于线路车站以两线T 型交叉部位为分界的两部分结构的中部偏远离交叉部位处，T 型换乘车站结构位移的最小部位发生在两线车站结构的交叉部位。

3.3.1.2 水平位移差

根据动力时程分析结果，选取结构截面水平位移的最大部位，进行截面顶底的水平位移差分析。1 线车站和2 线车站分别选取X 方向和Y 方向输入地震波工况进行分析。图12 给出了工况1 下，即X 方向的地震作用下，断面1-1～断面1-3 顶底的水平位移差时程曲线；图13 给出了工况4 下，即Y 方向的地震作用下，断面2-1～断面2-4 顶底水平位移差时程曲线。

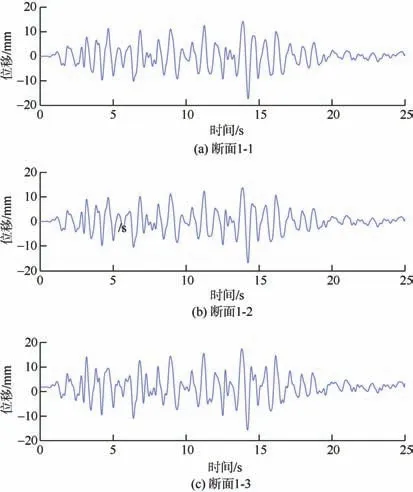
图12 工况1 中1 线各断面处顶板和底板的位移差时程曲线 Figure 12 Time history curve of the displacement difference between the top plate and the bottom plate at each section of line 1 in the working condition 1

由图12、13 可知，在相同的地震动输入情况下，T 型换乘车站结构各断面顶底水平位移差时程曲线的波动趋势相同，均在同一时刻达到最大值；1 线车站各断面顶底的水平位移差时程曲线形状相似，2 线车站各断面顶底的水平位移差时程曲线形状也相似，但两站做对比，断面顶底的水平位移差时程曲线形状差异明显。

表3、4 分别给出了工况1～6 各断面顶底水平位移差的最大值。由表可知，在X 方向地震动作用的各工况中，换乘车站顶底水平位移差的最大值发生在断面1-1 处，最大值为17.32 mm，对应层间的位移角为1/1213，断面1-1～断面1-3 的顶底水平位移差依次减小；在Y 方向地震动作用的各工况中，换乘车站结构顶底水平位移差的最大值位于断面2-1 处，最大值为11.15 mm，对应层间位移角为1/1210；对于结构顶底的水平位移差，断面2-1 大于断面2-2，断面2-4、断面2-3、断面2-2 依次减小。

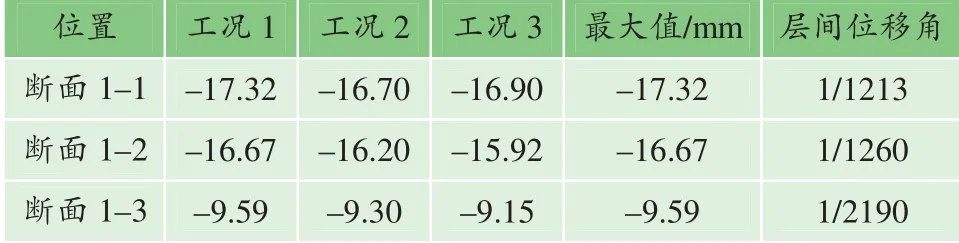
表3 X 方向地震作用下结构顶、底的水平位移差及位移角 Table 3 Displacement difference and displacement angle between the top and bottom of the structure under the X-direction earthquake

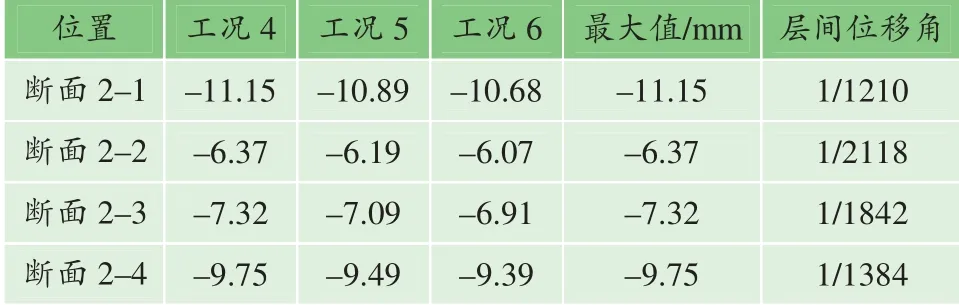
表4 Y 方向地震作用下结构顶底的水平位移差及位移角 Table 4 Displacement difference and displacement angle between the top and bottom of the structure under the Y-direction earthquake

由以上分析可知，在E2 水平地震作用下，输入同一条地震波时，T 型换乘车站结构顶底的水平位移差时程曲线的波动趋势相同，且在同一时刻达到最大值；在相同覆盖土层厚度条件下，结构顶底的位移差随结构高度的增加而增大；结构截面顶底水平位移差的最大值出现在地下3 层车站的结构，沿该车站的纵向，位于车站结构中部偏远离交叉部位处；对于车站主体结构，两线T 型交叉部位截面顶底的水平位移差最小。

3.3.2 E3 地震作用下结构变形分析

3.3.2.1 最大水平位移

图14 X 方向位移的最大值 Figure 14 Maximum displacement in X direction

在工况7～工况9 中，即在X 方向E3 地震荷载作用下，换乘车站结构沿X 方向水平位移的最大值分布云图如图14 所示。由图可知，换乘车站结构沿X 方 向的水平位移随结构在土层中的深度减小而增大，最大值均发生在1 线车站主体结构的顶板部位，该部位沿1 线车站纵向，位于车站中部偏远离两线交叉的部位处，最大值分别为74.86、72.61、71.11 mm；换乘车站结构沿X 方向水平位移的最小值位于两线车站的交叉部位，换乘车站各出入口及风道结构沿X 方向的水平位移均小于车站主体结构的位移。

在工况10～工况12 中，即在Y 方向E3 地震荷载的作用下，换乘车站结构沿Y 方向水平位移的最大值分布云图如图15 所示。由图可知，换乘车站结构沿Y方向水平位移的最大值分别为74.89、72.61、71.15 mm，最大值均发生在2 线车站主体结构的顶板部位，该部位沿2 线车站纵向，位于两线车站以两线车站交叉部位 为分界的两部分的中部、偏远离两线交叉的部位处；换乘车站结构沿Y 方向水平位移的最小值位于两线车站的交叉部位。各工况在换乘车站各出入口及风道沿Y方向的水平位移均小于车站主体的位移。

图15 Y 方向位移的最大值 Figure 15 Maximum displacement in Y direction

由以上分析可知，在E3 水平地震作用下，T 型换乘车站结构的最大水平位移的分布规律与E2 地震作用下的规律相似，即随结构在土层中的深度增加而减小；T 型换乘车站水平位移的最大部位出现在垂直于输入地震动方向的3 层线路车站，沿该线路车站纵向，水平位移的最大值位于线路车站以两线T 型交叉部位为分界的结构中部偏远离交叉部位处；T 型换乘车站结构位移的最小部位发生在两线车站结构的交叉部位。换乘车站各出入口及风道的水平位移均小于车站主体的位移。

3.3.2.2 水平位移差

图16 给出了工况7 下，即X 方向E3 地震作用下断面1-1～断面1-3 顶底的水平位移差时程曲线；图17 给出了工况10 下，即Y 方向地震作用下断面2-1～断面2-4 顶底的水平位移差时程曲线。

图16 工况7 下1 线各断面处顶板和底板的 位移差时程曲线 Figure 16 Time history curve of displacement difference between top plate and bottom plate at each section of line 1 under working condition 7

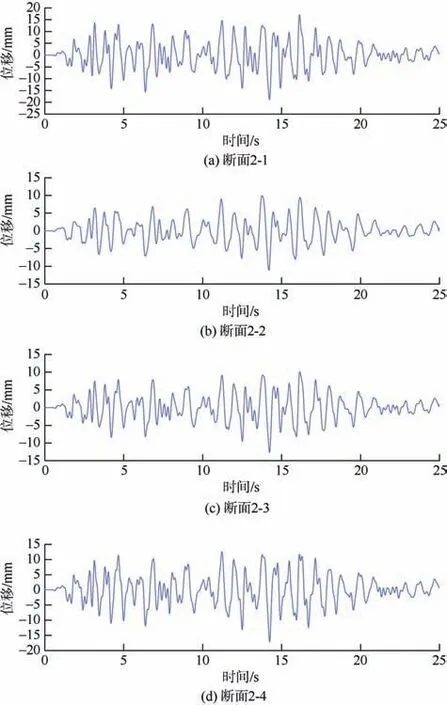
图17 工况10 下2 线各断面处顶板和底板的 位移差时程曲线 Figure 17 Time history curve of the displacement difference between the top plate and the bottom plate at each section of line 2 under working condition 10

由以上分析可知，在相同的地震动输入情况下，T 型换乘车站结构各断面顶底的水平位移差随时间波动的趋势相同，且均在同一时刻达到最大值；1 线车站各断面顶底的水平位移差数值随时间波动的状况相近，2 线车站也呈现同样的规律，但两线的车站相比，断面顶底的水平位移差随时间变化的差异显著。

表5、6 分别给出了工况7～12 各断面顶底水平位移差的最大值。由表可知，在X 方向地震动作用的各工况中，换乘车站顶底水平位移差的最大值发生在断面1-1 处，最大值为29.26 mm，对应层间位移角为1/718，断面1-1～断面1-3 的顶底水平位移差依次减小；在Y方向地震动作用的各工况中，换乘车站结构顶底位移差的最大值位于断面2-1 处，最大值为18.83 mm，对应层间位移角为1/716；对于结构顶底位移差，断面2-1 大于断面2-2，断面2-4、断面2-3 断面2-2 依次减小。

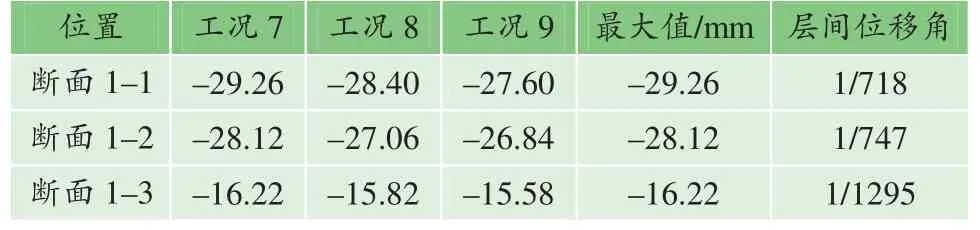
表5 X 方向地震作用下结构顶底的水平位移差及位移角 Table 5 Displacement difference and displacement angle between the top and bottom of the structure under the action of the X-direction earthquake·

表6 Y 方向地震作用下结构顶底的水平位移差及位移角 Table 6 The displacement difference and displacement angle between the top and bottom of the structure under the action of the Y-direction earthquake·

由以上分析可知，相同E3 地震动输入时，T 型换乘车站结构各断面顶底水平位移差的大小随时间波动的趋势相同，且在同一时刻达到最大值；在相同覆盖土层厚度的条件下，3 层线路车站结构截面顶底的位移差大于2 层线路车站结构的相应位移差；结构顶底水平位移差的最大值出现在地下3 层车站，沿该车站纵向，位于车站结构中部偏远离交叉部位处；对于车站主体结构，两线T 型交叉部位顶底的水平位移差最小。

4 结语

以南京某T 型换乘车站结构为例，采用动力时程分析方法，建立场地土-T 型换乘车地铁车站结构的三维动力有限元计算模型，通过从不同方向输入地震动和改变输入地震动峰值加速度的方式，研究在不同地震动输入的情况下T 型换乘车站结构的位移响应规律，主要结论如下：

1) 在车站结构位于软土地层条件下，T 型换乘车站结构的水平位移随其所处土层深度的增加而减小，最大水平位移出现在结构顶板部位。

2) 在相同覆盖土层厚度的条件下，3 层车站结构的最大水平位移及截面顶底的水平位移差大于2 层车站的相应值。

3) T 型换乘车站结构，其最大水平位移及截面最大顶底的水平位移差均出现在垂直于输入地震动方向的线路车站；沿该线路车站纵向，水平位移的最大值及车站顶底水平位移差的最大值，均出现在远离T 型交叉部位；T 型换乘车站结构水平位移的最小值及截面顶底位移差的最小值均发生在车站T 型交叉处。

4) T 型换乘车站结构，其各断面顶底水平位移差的大小随时间波动的趋势基本相同，且在同一时刻达到最大值；当两线车站的结构形式不同时，两线车站顶底的位移差随时间的波动差异明显。