基于实测数据的随机振动疲劳寿命预测方法

董江，于浩，文敏，张强波，郭海东

（中国飞行试验研究院，西安 710089）

0 引言

机械结构或部件因承受交变载荷而导致疲劳是其最常见的失效原因。因此，在设计过程中采取快速、有效的方法预估疲劳寿命是至关重要的。目前关于随机振动疲劳与常规循环疲劳的本质区别的研究较少,关于振动疲劳的定义尚不明确。振动载荷下的结构应力/应变量值及循环次数与外载荷量值、作用时长及结构动态特性有关。

关于随机振动载荷下的构件疲劳寿命预测，其关键在于确定加载历程、载荷循环数及统计各循环损伤分布以评估总的疲劳损伤。随机振动疲劳寿命预估方法主要分为时域法和频域法。Mrsnik等研究对比了Wirsching-Light、Gao-Moan 以及Dirlik 等频域法估算寿命时的优缺点。Pothula 等分别运用Dirlik、Narrow-band、Tunna 及Steinberg等频域方法预估了不同功率谱密度下的试件疲劳寿命，结果表明Dirlik 法更接近试验值。张炜等对车载电子设备进行了随机振动和疲劳损伤分析，采用频域方法分析了电子设备故障机理并对其使用寿命进行了预估。Eldoan 等采用Dirlik 法及雨流计数法预估了变频恒幅振动载荷下的悬臂梁构件疲劳寿命，二者结果较为相近。陈华等采用时域法预估了某结构的疲劳损伤。Sobczyk 等对时域法进行了研究，并预估结构的疲劳寿命。频域法预估寿命时，将疲劳寿命表示为激励谱特征的函数，但目前没有一个通用的解析解。时域法预估寿命时，主要依赖于时间历程上的应力或应变幅值，但若无实测数据，采用计算机模拟所有可能的应力‒时间历程样本耗时较大，在结构设计阶段无法获取完整的载荷历程。工程使用中，若能够获得结构时域内的应力‒时间数据，则通过雨流计数法预估随机振动疲劳寿命是普遍接受的。

针对时域法应力‒时间历程模拟耗时较长的问题，本文开展基于实测应力历程数据的试件随机振动疲劳寿命预估方法研究。首先进行3 个振动量级下的试件随机振动疲劳试验，获取试件危险点的应变响应历程；然后基于雨流计数法进行载荷循环计数，统计载荷幅值及均值分布；最后结合线性累积损伤理论预估试件疲劳寿命，并与试验值进行对比，以验证该疲劳寿命预测方法的可行性与有效性。

1 随机振动寿命计算理论

随机振动不能用确定的函数关系式来表达，是一种只能在统计意义下描述的振动。随机过程()的任一样本函数()的功率谱密度函数S()与自相关函数R()是一傅里叶变换对：

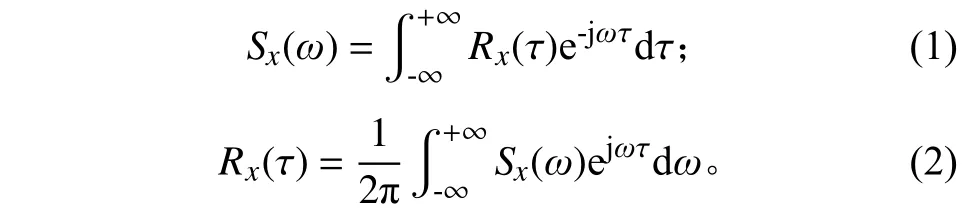
其中，

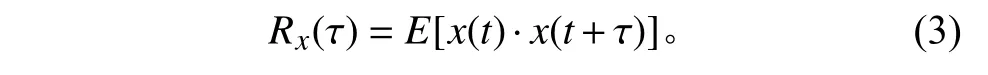
随机过程的时域特性由相关函数进行描述，由功率谱密度函数描述其频域特性。双边功率谱密度函数可由式(1)定义，考虑到实际工程中的频率均≥0，单边功率谱密度函数()为

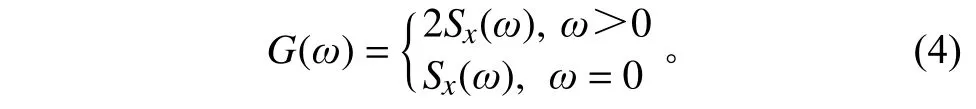
构件的随机振动过程的激励和响应均为随机过程，在频域中表述更为方便，对于具体构件而言，随机振动载荷造成的损伤效果是在时域内逐步累积的，且经典疲劳评估方法也是建立在应力的时域分析基础上。因此若有构件时域内的载荷实测数据，则可采用时域法对疲劳寿命进行预估。时域法预估寿命的基础是损伤累积，即每个载荷子步下的损伤因子累积。随机振动的时域应力幅值是随机的，但在统计意义下是规律的，可采用循环计数原理统计载荷幅值信息。

1.1 累积损伤理论

工程上广泛应用的线性累积损伤理论为Palmaram-Miner 理论，即认为级交变应力引起的疲劳损伤相互独立，可线性累加，且当损伤累积达到某一特定数值时，结构将发生破坏。结构累积损伤值可以表示为

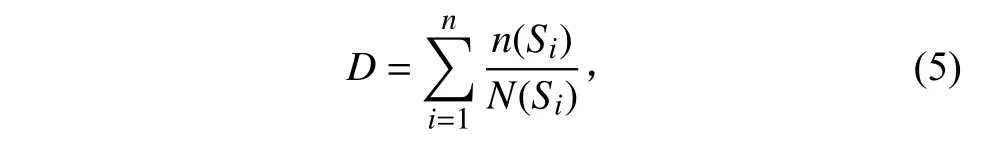
式中：(S)为疲劳曲线上应力水平S时的寿命循环数；(S)为应力水平S时1s 内实际作用的循环数。

Miner 通过引入临界损伤值来判定结构疲劳失效，则结构的疲劳寿命为

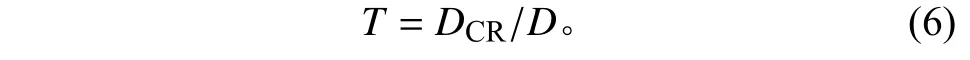
通常认为=1，载荷加载次序影响下会导致偏离1 很大，但是对于随机载荷作用下，载荷加载次序效应不明显，在1 附近。

1.2 雨流循环计数法

雨流循环计数法是一种二参数循环计数法，主要功能是将经过伪读数去除、峰谷值检测、无效幅值去除后的实时载荷历程简化为若干载荷循环，以供疲劳寿命估算。雨流计数法是基于材料的应力‒应变迟滞回线进行循环计数的，较好地反映了随机加载的全过程。

雨流计数法将应力‒时间历程顺时针旋转90°，使时间坐标轴竖直向下（如图1 所示），其基本原则如下：

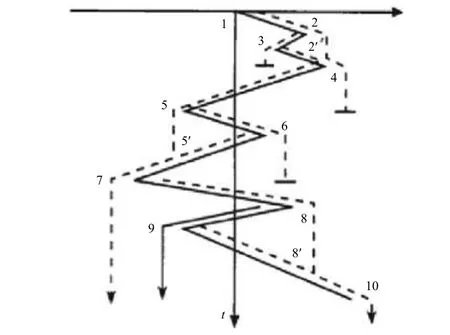
图1 雨流计数原理Fig.1 The principle of rain flow counting

1）雨流的起点依次在每个峰值（或谷值）的内侧，即“屋顶”；

2）雨流流到下一个峰值处（或谷值）竖直下落，直到遇到一个比其更大的峰（或更小的谷）为止；

3）当雨流遇到来自上面屋顶流下的雨流时，就停止流动，并构成一个循环；

4）根据雨流的起点和终点，得到各个循环，并逐一提取出来，记录下各自的幅值或均值。

在应用雨流计数法进行数据统计之前，通常对数据序列进行调整，减少载荷循环的缺失，形成完全雨流计数法。基于MATLAB 开发相应的雨流计数法程序，具体流程如图2 所示。

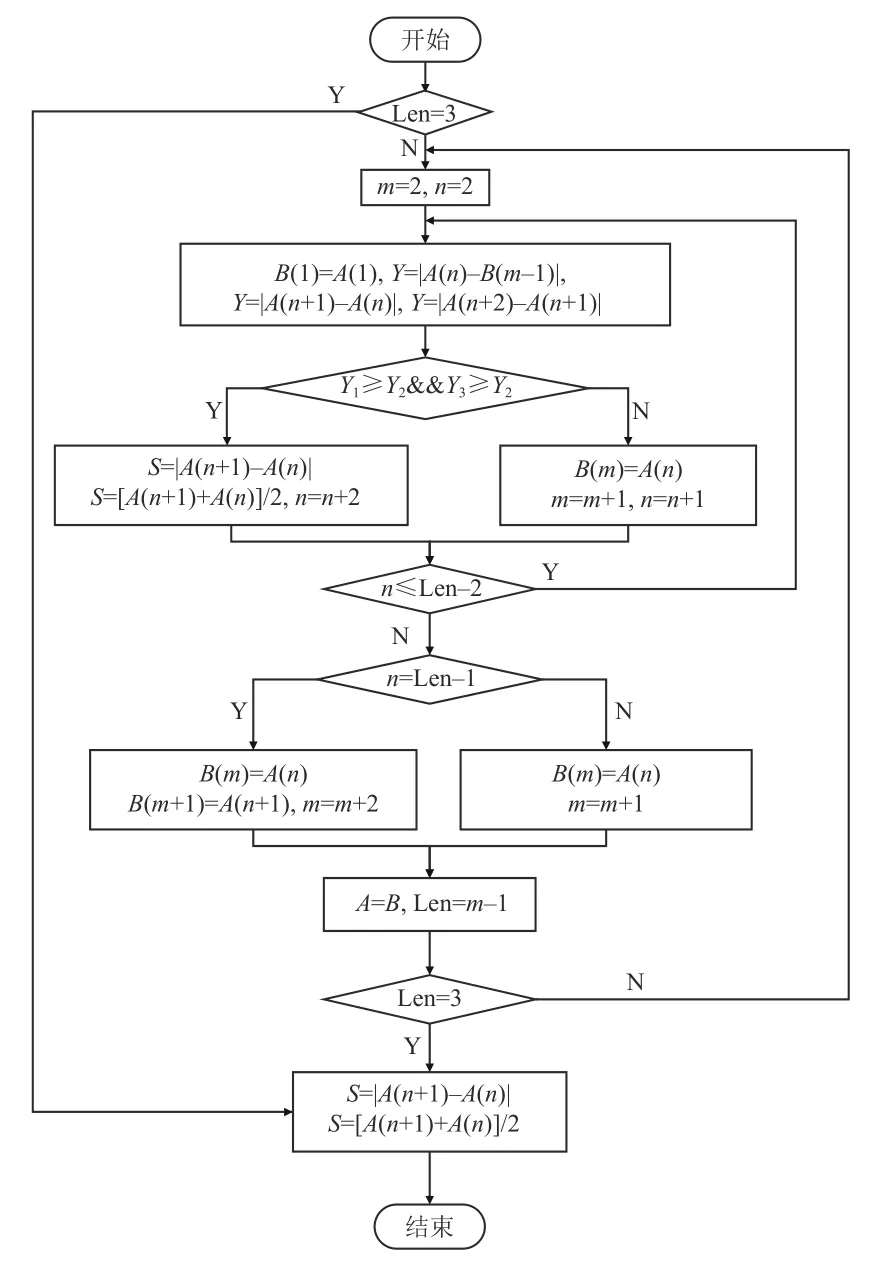
图2 雨流计数法程序框图Fig.2 Flow chart of the rain flow counting method

2 随机振动疲劳试验

2.1 试验方案

参考文献[19-20]中的振动疲劳试件设计，疲劳试件尺寸如图3 所示，材料为1Cr18Ni9Ti 不锈钢，试件固有频率为80.1Hz。采用DC-1000 振动台进行随机振动疲劳试验。

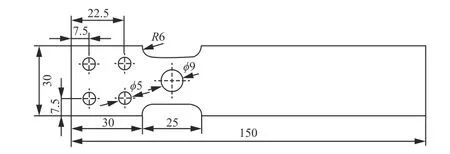
图3 疲劳试件尺寸Fig.3 The dimensions of specimen for random vibration fatigue test

疲劳加载条件下，构件的裂纹形成包括裂纹孕育、萌生、扩展和瞬断等阶段，而前三个阶段构成构件的疲劳裂纹萌生期。有学者认为裂纹萌生期约占整个疲劳寿命期的80%。试件振动疲劳过程中以试件表面出现明显裂纹时所对应的循环数为当前载荷下的模拟试件振动疲劳寿命，即裂纹萌生寿命。试件萌生裂纹后，裂纹迅速扩展，由文献[2]可知，试件出现裂纹后其固有频率将发生变化，同一振动量级下振动微应变将发生变化，因此在振动疲劳试验中可通过对试件进行应变计改装来监测其疲劳过程中的应变历程及固有频率变化，以确定其疲劳寿命，具体如图4 所示。另外，为准确获得各振动量级下危险点的振动应变也需要进行应变计改装。本文采用虚拟载荷校准技术确定应变计改装位置与裂纹萌生点的应力比关系，图5为试件有限元分析应力云图与试验中裂纹萌生位置对比，裂纹萌生位置即对应仿真应力最大位置。

图4 振动应变监视Fig.4 Vibration strain monitoring

图5 试件应力的有限元模拟结果与试验结果比较Fig.5 Comparison of finite element simulation and experiment result

具体试验方法及流程如下：

1）每10 个试件为一组，将其安装于夹具上，每个试件完成应变计改装并进行振动应力的实时监测，如图6 所示；

图6 试件随机振动疲劳试验Fig.6 Random vibration fatigue test of the specimens

2）采用图7 所示谱图（宽带基础激励为0.03/Hz）开展随机振动疲劳试验，其中=3.5/Hz；

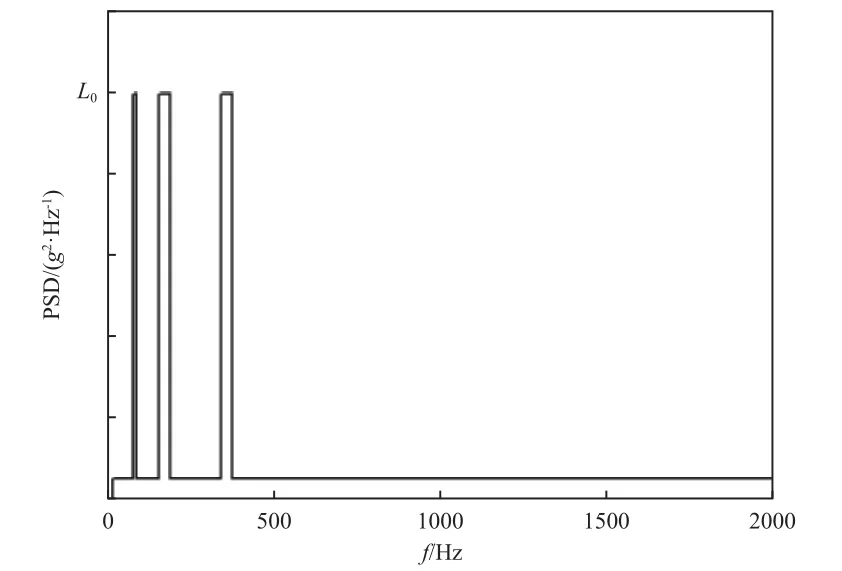
图7 随机振动疲劳试验施加的功率谱密度Fig.7 The power spectral density(PSD) load in the random vibration fatigue test

3）实时监测试件表面振动应变直至试件产生裂纹，记录失效时间；

4）若存在少量超过已疲劳试件平均寿命的3 倍分散带仍未产生裂纹，则停止试验；

5）重新设定振动量级=5.5/Hz 及=7.5/Hz，重复上述1）～4），完成不同量级下的试件随机振动疲劳试验。

2.2 试验结果

图8 给出了振动量级为7.5/Hz 时3#试件产生裂纹失效过程的振动应变数据，可以看出：当试件尚未失效时振动应变处于较高水平；在某一时刻试件孔边萌生裂纹时，振动应变明显下降（降低约50%）；而后振动应变保持在低水平不变。统计多种振动量级下的试件失效情况，振动应变的变化情况均与此相同，因此通过应变实时监测的方法可以判断试件失效的时刻。

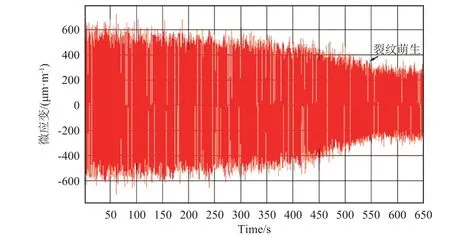
图8 振动应变监测下的试件失效过程Fig.8 Failure process of specimens under vibration strain monitoring

3 种振动量级下试件的随机振动疲劳失效时间见表1。其中：3.5/Hz 下，试件平均疲劳寿命为21.74h，6#及10#试件的试验时间远大于平均寿命而未失效，停止试验；5.5/Hz 下，试件平均疲劳寿命为7.64h，2#及4#试件的试验时间远大于平均寿命而未失效，停止试验；7.5/Hz 下，试件平均疲劳寿命为4.28h，9#试件的试验时间远大于平均寿命而未失效，停止试验。

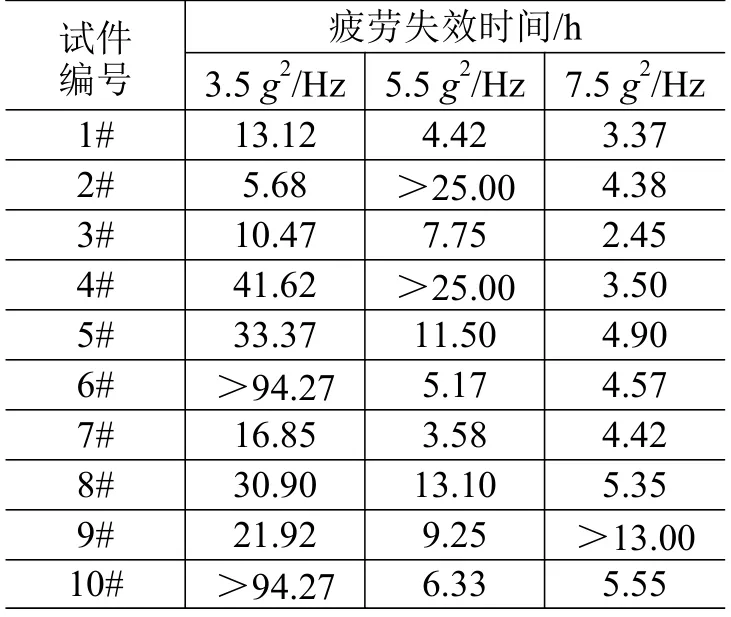
表1 各振动量级下的试件疲劳失效时间Table 1 Fatigue failure time of specimens in different vibration levels

3 随机振动寿命预估

随机振动载荷作用下的结构应变响应为随机过程，其在时域中需使用无穷多组时间无限长的样本曲线来描述，历经随机过程的任意一条样本曲线上包含了该随机过程的所有统计特性。一般工程实际中，随机振动载荷都可以假设为各态历经的随机过程，即可以抽取任意一条样本曲线进行寿命估算，本文各试件选取4 段时域响应数据估算寿命进行平均。

图9 为7.5/Hz 振动量级下某试件危险点应变时域值，数据时长=3min（采样率f=4800Hz）。根据试件材料属性将图9 中时域应变转化为时域应力值并进行雨流计数处理后，由Goodman 平均应力模型修正后得到的应力幅值概率分布模型，及应力幅值的正态分布、Reyleigh 分布及Weibull 分布拟合，结果如图10 所示。由图可见：相比于Reyleigh 分布模型，正态分布模型及Weibull 分布模型均能较好地描述其概率密度，但正态分布模型在中小应力区拟合程度不如Weibull 分布模型。因此综合考虑，认为Weibull 分布模型能够较好描述雨流幅值概率分布。相关文献也表明，大多数情况下载荷幅值服从Weibull 分布。

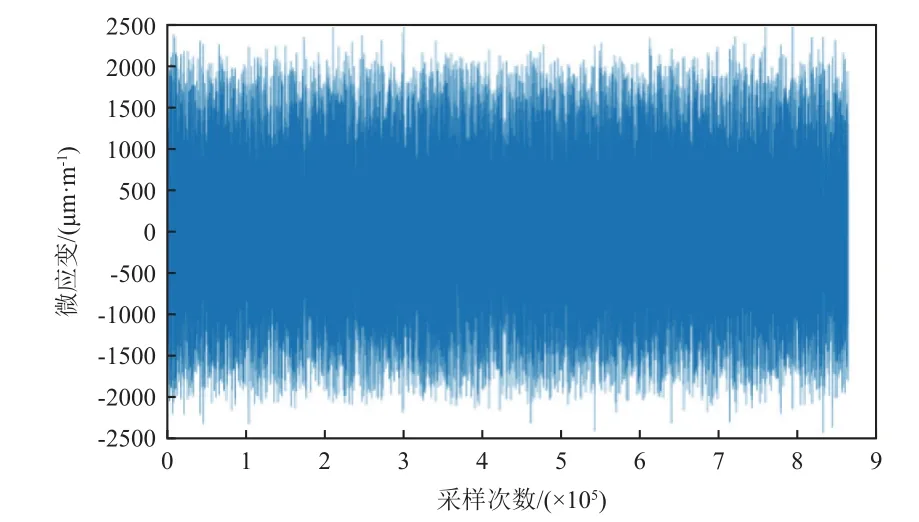
图9 试件应变时域响应Fig.9 Time-domain response of specimen strain

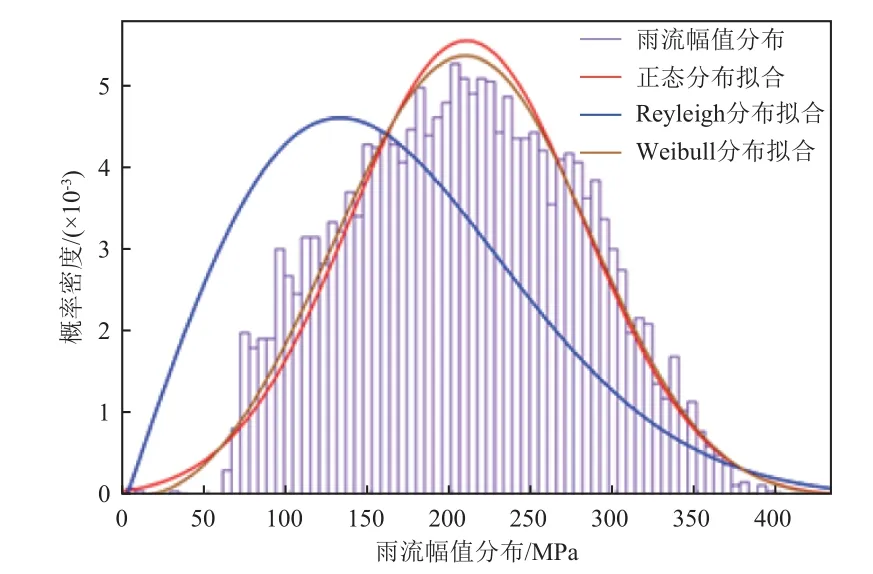
图10 应力幅值概率模型对比Fig.10 Comparison of probability models for expressing the stress amplitude

随机振动疲劳的载荷具有不确定性，若统计时间足够长的话，其载荷是有一定的周期性。选取时域响应样本进行疲劳寿命预估时，需考虑所选时间段长度，因为过短的时间段无法代表整个随机过程，而过长的时间段则会增加计算量。为确定所选取样本长度，分别选取10s、30s、40s 及60s 时域数据进行雨流计数处理，统计其雨流幅值概率分布及累积概率密度，确定合适样本长度，具体如图11、12所示。由图11 可知，4 种时间段下应力幅值均符合Weibull 分布模型，且随着时间段增加，拟合效果更好。由图12 可知，当时间段大于40s 时，应力幅值的累积概率密度分布几乎重合，即该时间段内各应力幅值的占比相等，因此可选取40s 时间段代替无限长时间时域响应信号。

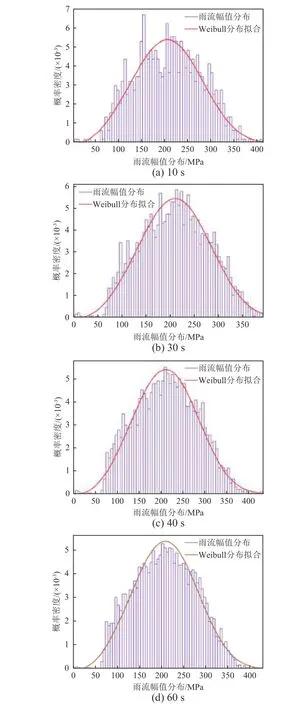
图11 应力幅值概率模型Fig.11 The probability models of stress amplitude

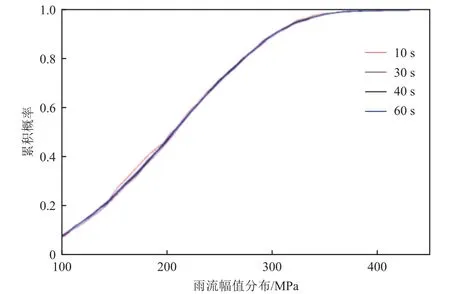
图12 4种时间段的应力幅值累积概率密度分布Fig.12 Cumulative probability density distributions of stress amplitude in different time durations

基于试验中试件的时域应变响应信号，再经雨流计数法处理后，应用Miner 线性累积损伤理论结合图13 中材料S-N 曲线对试件在3 种振动量级下的随机振动寿命进行预估，结果如表2、表3 及表4所示，由于应变计零漂、毛刺信号等问题会影响试件真实载荷历程，所以各组选取的预估试件少于10 件，共18 件。

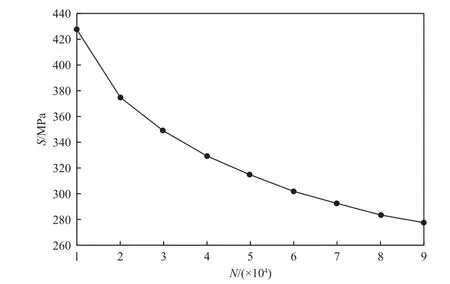
图13 1Cr18Ni9Ti 材料S-N 曲线Fig.13 The S-Ncurve of 1Cr18Ni9Ti

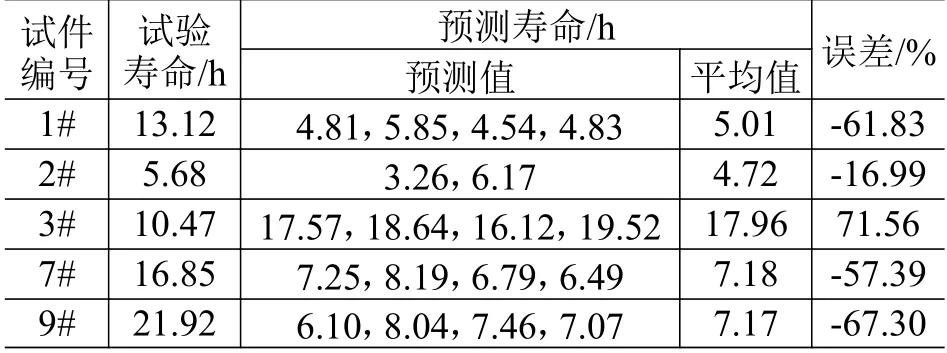
表2 3.5g2/Hz 时试件疲劳寿命对比Table2 Comparison of specimens’fatigue life at 3.5g2/Hz

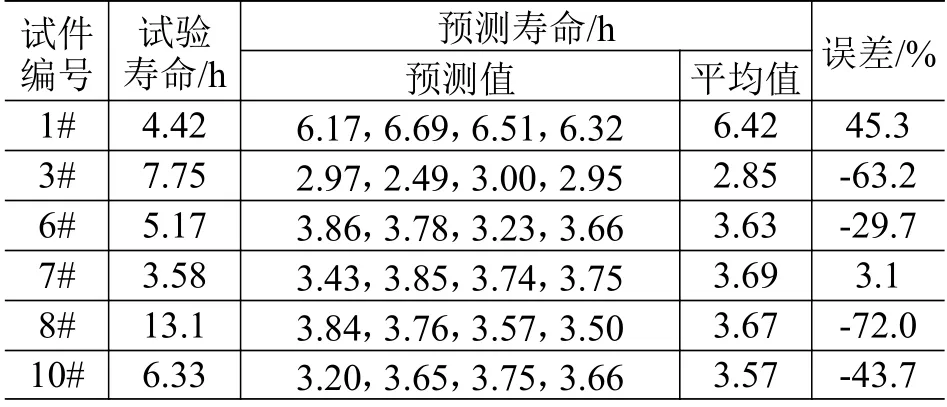
表3 5.5g2/Hz 时试件疲劳寿命对比Table3 Comparison of specimens' fatigue life at 5.5g2/Hz

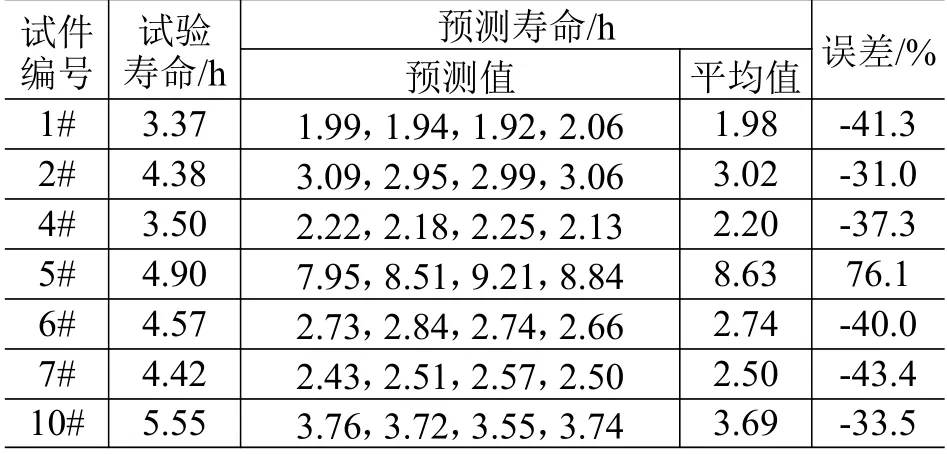
表4 7.5g2/Hz 时试件疲劳寿命对比Table4 Comparison of specimens' fatigue life at7.5g2/Hz

图14 为3 种振动量级下18 件试件的预估寿命在试验寿命3 倍分散带内的分布，其中，试件编号根据试验寿命按升序排列后重新定义。由图可知：18 件试件的预估疲劳寿命均在试验疲劳寿命3 倍分散带内，属工程误差范围内；另外大多数试件的预估寿命小于试验值，表明由基于实测载荷的雨流计数法预估构件随机振动寿命具有更高的保守性。造成误差的原因可能有：1）试件加工尺寸精度与模型设计尺寸存在差异；2）未考虑尺寸效应影响，仅采用危险点的最大应变进行疲劳寿命估算。

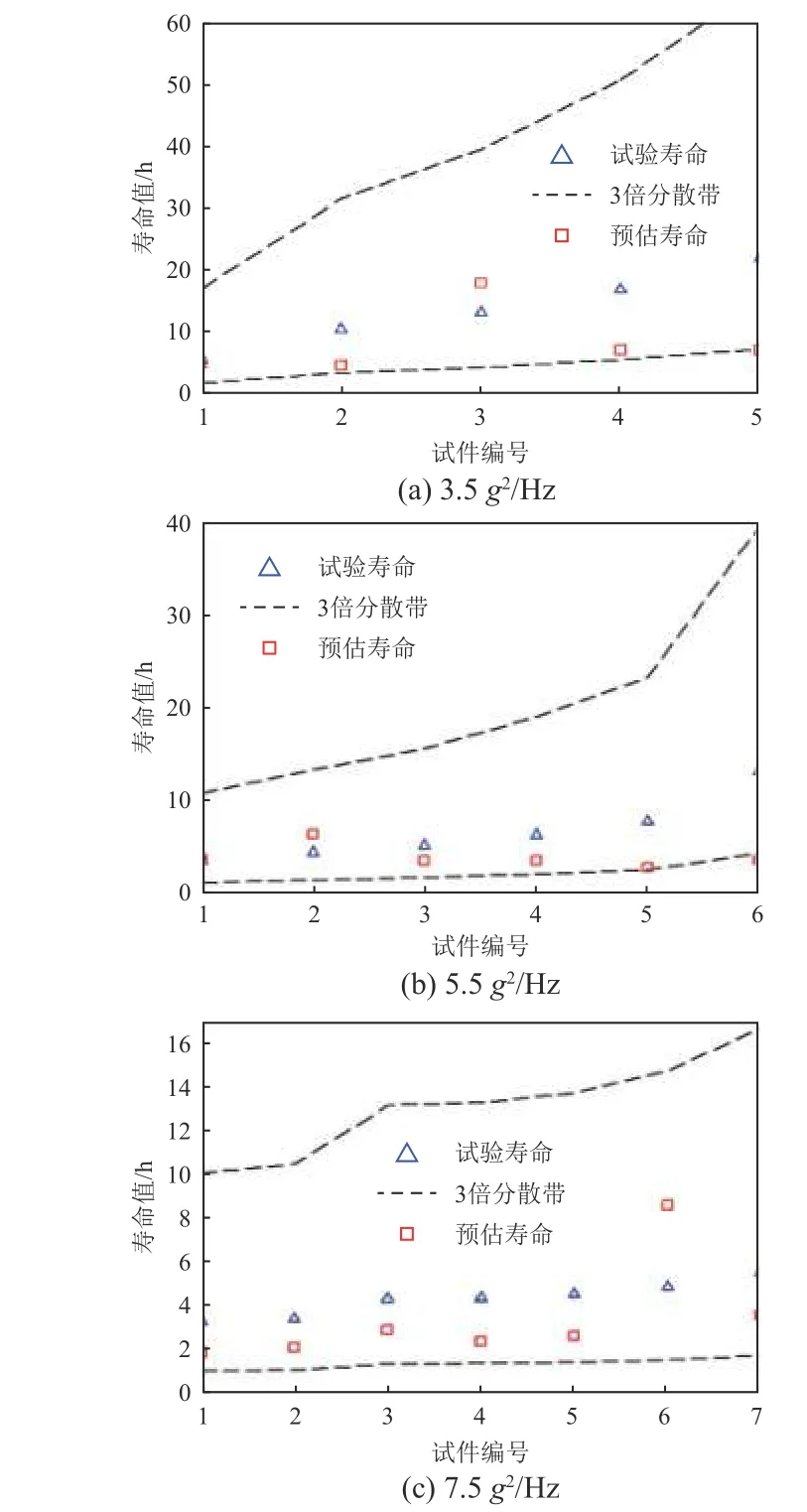
图14试件预估寿命3 倍分散带分布Fig.14 Triploid dispersion band distribution of predicted life of the specimens

4 结论

本文采用振动台开展了3 种量级下的试件随机振动疲劳试验，对试验过程中的振动载荷进行了实测，基于实测时域数据预估了试件的随机振动疲劳寿命，得出结论如下：

1）通过改装应变计采集试验中的试件应变响应历程，可实现对随机振动疲劳试验过程中试件破坏瞬间的监测；

2）对实测载荷数据进行雨流循环计数统计获得其应力幅值概率分布模型，可由Weibull 分布模型最优拟合；

3）开展3 种量级下的试件随机振动疲劳试验，获得试件危险点的时域应变响应历程，基于雨流计数法及线性累积损伤理论预估的疲劳寿命与试验值对比均在3 倍分散带内；

4）试验结果验证了基于实测时域数据的结构件随机振动疲劳寿命预测方法的可行性及有效性，后续可通过载荷数据的实测开展危险结构件的疲劳失效监测及寿命预测。