基于公共自行车调度的系统布局规划模型研究

邵 卿，陈清化，王熙杰，田宇璐

（湖南铁路科技职业技术学院，湖南 株洲 412006）

0 引言

自行车交通作为解决城市交通拥堵和公共交通出行“最后一公里”难题的有效方法，在全国各大城市得到了大力推广。目前对公共自行车系统布局的研究，大多是着眼于运营模式、规模测算和租赁点选址等方面；而对于公共自行车系统调度方面的研究，则大多为建设运营过程中的自行车调配或实时动态调度。何流[1]分析了目前公共自行车的使用特征与问题，建立由自适应遗传算法和方式分担交通分配组合反馈模型组成的双层模型进行求解，得到最优布局方案。刘新宇[2]将一天分为二十个时段，设立自行车系统供需平衡的前提，建立了一个最小化总投资建设成本的自行车租赁系统规划模型。朱从坤[3]建立多元Logit模型和多元线性回归模型预测其客流量，并提出基于用户满意度和车辆（桩）周转率的租赁点规模测算方法，为公共自行车租赁点的规划及建设提供了量化依据。方云飞[4]以公交站点为中心，建立以最大化满足用户需求量为优化目标的公共自行车选址的非线性优化模型。Lin Jenrong[5]建立基于系统服务水平的数学模型求解自行车租赁站点选址、数量和车道的网络结构。姚学儒[6]将运营时间划分为多个时间段，以最小化未满足需求为目标函数，构建规划模型确定公共自行车系统租赁点位置、桩位配备数量。Sin C[7]研究了静态自行车复位问题，建立了一个求各个站点总惩罚最小的模型，提出了一个迭代禁忌搜索启发式算法，所得结果包括选择一系列要去的站点并定序，并决定各站点的装卸数量。

本文基于以上文献研究基础，将公共自行车系统布局与公共自行车系统调度两者结合考虑，从居民出行需求的发生与吸引量和公共自行车系统外部供给及内部满足等角度出发，构建考虑有调度的公共自行车租赁点布局规划模型。

1 问题提出

公共自行车系统的一般性网络结构如图1所示。在某规划区域内有n个自行车需求点，m个候选自行车租赁点，现需要选择部分候选租赁点进行建设，并在这些租赁点分配一定数量的自行车和停车桩，以满足一天内各个时段的居民出行需求，做到任一时段在居民步行范围内的租赁点都能租还车辆，同时又使得规划区域内居民总出行时间最短。

图1 公共自行车系统网络结构Fig.1 Network structure of public bicycle system

居民出行时间包括：起始需求点到租赁点的时间、租赁点到租赁点的时间和租赁点到目的需求点的时间三个部分。将7—19点这段时间划分为6个时段进行研究，其中7—9点早高峰时间为时段1；9—11点为时段2；11—13点为时段3；13—15点为时段4；15—17点为时段5；17—19点晚高峰时间为时段6。

2 模型构建

2.1 模型假设

模型涉及参数较多，过程复杂，应在满足可操作性的基础上尽量考虑主要影响因素，使模型尽量接近实际情况。基于上面的问题描述，为了便于建立模型，本文作出以下假设：（1）出行者知道步行范围内哪些租赁点可提供自行车和空的停车桩，每次总是去这些租赁点借车和还车；（2）各个需求点的出行是规划区域内的出行，不考虑区域外的出行对各个需求点产生的影响；（3）各个需求点之间的自行车出行量已知；（4）每个租赁点的固定建设成本相同；（5）全天的自行车出行量集中在7—19点之间，其余时间自行车的借还需求很小，不纳入研究范围；（6）运输车辆没有行驶时间和行驶里程的限制；（7）调度用的运输车辆为同一类型，从停车场出发，完成调配任务后再返回停车场。

2.2 参数和变量

（1）决策变量：

yj表示如果在候选区域j建设租赁点则yj=1，否则yj=0；

ParkPile(j)表示在候选租赁点j分配的停车桩数；

Bike(j)表示在候选租赁点j分配的自行车数；

ev表示运输车辆v的路径决策变量，若车辆v被使用，则ev=1，否则ev=0；

xjj'v表示租赁点j调度服务的决策变量，车辆v在租赁点j'结束调度工作后，再到租赁点j进行调度，则xjj'v=1，否则xjj'v=0。

（2）其他变量：

Biji'(t)表示第t个时段需求点i到需求点i'的出行者在候选租赁点j的借车数；

Rij'i'(t)表示第t个时段需求点i到需求点i'的出行者在候选租赁点j'的还车数；

Eijj'i'(t)表示第t个时段需求点i到需求点i'的出行者在候选租赁点j所借的自行车中还到候选租赁点j'的自行车数；

Xj(t)表示第t个时段初第j个候选租赁点空闲的停车桩数；

Pj(t)表示第t个时段第j个候选租赁点可以提供的自行车数；

Qj(t)表示第t个时段第j个候选租赁点可以提供的空闲的停车桩数；

Cj(t)表示第t个时段第j个候选租赁点所需的自行车的借还需求差，即调度需求量。

（3）常量：

dij表示第i个需求点到第j个租赁点的距离；djj'表示第j个租赁点到第j'个租赁点的距离；d0表示出行者步行距离上限；IG表示规划区域的总投资额；

表示最少需建设的自行车租赁点数目；表示最多能建设的自行车租赁点数目；

aij表示如果第i个需求点可以由第j个候选租赁点服务则aij=1，否则aij=0；M表示足够大的正整数；g表示每个自行车租赁点的固定建设成本；

f1表示每辆自行车的购买成本；f2表示每个停车桩的安装成本；

Oi(t)表示第t个时段第i个需求点的自行车出行发生量；

Di(t)表示第t个时段第i个需求点的自行车出行吸引量；

Wii'(t)表示第t个时段需求点i到需求点i'的自行车出行量；

α表示每个自行车租赁点最少需要分配的自行车数；

v1表示出行者的步行速度；v2表示出行者的骑车速度；dmin表示租赁点间最小距离；

ω表示自行车租赁点服务能力下限；η1表示停车桩数多于自行车数的下限（本文取其为0.1）；η2表示停车桩数多于自行车数的上限（本文取其为0.3）；

p表示车辆单位距离运行成本；r表示每辆运输车辆使用的固定成本。

2.3 模型构建

（1）第一阶段模型构建

第一阶段规划可以描述为在调度充分的条件下，即有调度车存在的情况，每个时段初，租赁点拥有的自行车数不受上一时段的自行车数影响，而是与本时段该租赁点服务范围内需求点的自行车出行发生量和出行吸引量有关。为达到使规划区域内所有出行者总出行时间最小的目标，来选择待建租赁点及分配各点自行车数和停车桩数。

在规划区域内，设I(i∈I)为需求点的集合，J(j∈J)为候选租赁点的集合，J1为建设的租赁点的集合，T(t∈T)为各个时段的集合。建立如下的自行车租赁点选址模型：

在上述建立的数学模型中：

式（1）为目标函数，使规划区域内所有出行者的总出行时间最短，该目标函数包括三部分：起始需求点到租赁点的时间、租赁点到租赁点的时间和租赁点到目的需求点的时间；

式（2）约束规划区域内自行车租赁点的建设数目；式（3）定义0-1矩阵，用来保证自行车租赁点只能为最大服务范围内的需求点提供服务；式（4）约束对于每一个需求点，至少有一个自行车租赁点为其服务；式（5）约束对于每个已决定建设的租赁点，要保证至少有一个需求点作为其服务对象；式（6）、（7）约束自行车出行者的借、还车需求只能在候选租赁点，且该租赁点需在步行距离范围内；式（8）、（9）约束只有位于起始需求点和目的需求点步行距离范围内且建设的租赁点之间才有自行车出行；式（10）约束整个规划区域内，自行车的购买成本、停车桩的安装成本和租赁点的固定建设成本应不超过总投资额；式（11）约束起始需求点到目的需求点的自行车出行量等于起始需求点的出行者在各个租赁点的借车数之和；式（12）约束起始需求点到目的需求点的自行车出行量等于到目的需求点的出行者在各个租赁点的还车数之和；式（13）约束起始需求点到目的需求点在一个租赁点的借车数等于该租赁点到其他租赁点的自行车数之和；式（14）约束起始需求点到目的需求点在一个租赁点的还车数等于其他租赁点到该租赁点的自行车数之和；式（15）定义每一天开始时刻初的每个租赁点都有车可用；式（16）定义每个时段每个租赁点所需的自行车的调配量；式（17）去除调配量的非负限制，即强调其可为负整数或0的特点，同时该变量也是两阶段模型间连接变量。当时Cj(t)＞0，代表租赁点j应调入的公共自行车数；当Cj(t)＜0时，代表租赁点j应调出的公共自行车数量为|Cj(t)|，当Cj(t)=0时，表示该时段该点不需要调度；式（18）定义每个时段初每个租赁点空闲的停车桩数；式（19）定义每个时段末每个租赁点剩余的空闲停车桩数；式（20）约束任一时段，可为某需求点提供服务的租赁点，可提供的自行车数应不小于该需求点总的借车需求；式（21）约束任一时段需求点范围内的租赁点得满足到该需求点总的还车需求；式（22）约束任一时段各个需求点在某个租赁点的借车数之和应不大于该租赁点可以提供租赁的自行车数；式（23）约束任一时段到各个需求点在某个租赁点的还车数之和应不大于该租赁点可以提供还车的空闲停车桩数；式（24）约束每个建设的租赁点最少需要分配的自行车数；式（25）、（26）约束只有建设的租赁点才分配自行车和停车桩；式（27）为候选租赁点是否建设变量的0-1约束；式（28）为部分决策变量的非负约束；式（29）为保证系统的鲁棒性及弹性，限制各租赁点的停车桩数大于其所能拥有的最多自行车数，确保车有所停，且其差值处于一个合适的范围；式（30）约束两个租赁点间距不能过小，否则可能重复建设，增大成本；式（31）是为了保证待建自行车租赁点的服务水平，约束只有借、还车总数超过某一定值时才允许在该候选租赁点建自行车租赁点，否则不允许建。

（2）第二阶段模型构建

第二阶段规划描述在确定了待建租赁点和各点的调配量的情况下，规划调度车辆的路线安排和分配，使得总运输成本最小。

当第一阶段最优后，即得到要建设的租赁点及相应调配量，然后第二阶段就根据第一阶段确定的决策变量，寻求最优方案，安排调度车辆路线。

对于待建的站点编号j(j∈J1)，为了方便起见，将车场编号定为0；设运输车辆编号v(v∈V)，则第二阶段模型如下：

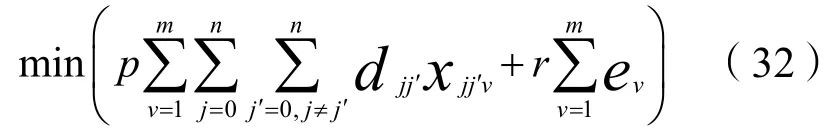
约束条件为：

其中，式（32）为第二阶段模型的目标函数，即使得总运输成本最小，运输成本则包括固定成本和可变成本这两个基本的部分；式（33）约束运输车辆的数量；式（34）限制调度车的运输容量；式（35）和式（36）表示各站点都被服务，且一辆车仅服务一次；式（37）表示车辆v为租赁点j调度服务的决策变量，车辆v在租赁点j'结束调度工作后，再到租赁点j进行调度，则xjj’v=1，否则xjj’v=0 ；式（38）表示运输车辆v运输路径的决策变量，若车辆v被使用，则ev=1，否则ev=0。上述模型中的j，j'∈J1（J1为待建设的租赁点，即yj），Cj(t)由第一阶段规划决策确定。

3 算例分析

3.1 算例简介

现拟在某规划区域内建设一个公共自行车租赁系统，投资总额为200万元。目前已经根据居民的出行需求确定了10个自行车出行需求点，并依据这些需求点确定了20个候选租赁点的位置。现在需要从这20个租赁点中选择部分租赁点建设，并分配相应数量的自行车和停车桩，以满足一天内各个时段居民的出行需求，做到任一时段居民在其步行范围内的租赁点都能借到车和还出车，同时又使得规划区域内居民总出行时间最短。但租赁点的建设数目应在7～13之间，避免租赁点建设太多造成资源的浪费以及租赁点建设过少无法满足出行者的需求。规划区域内需求点和租赁点的分布如图2所示。

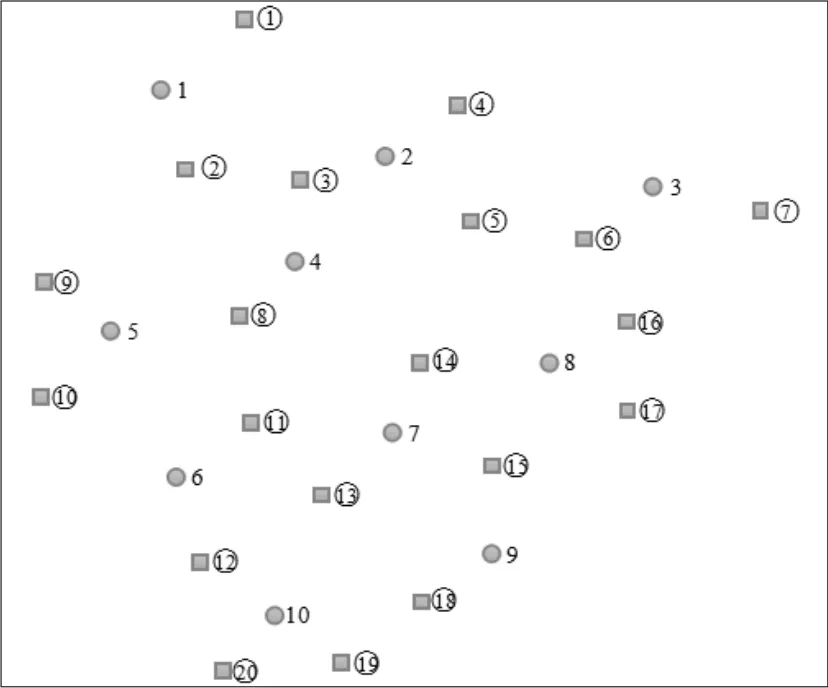
图2 需求点和租赁点分布图（●为需求点，■为租赁点）Fig.2 Distribution map of demand points and rental points（●：demand points，■：rental points）

候选租赁点和需求点之间的距离如表1所示。时段1各个需求点的公共自行车租借需求如表2所示。

表 1 租赁点到需求点的距离（单位：m）Tab.1 Distance from lease point to demand point（unit：m）

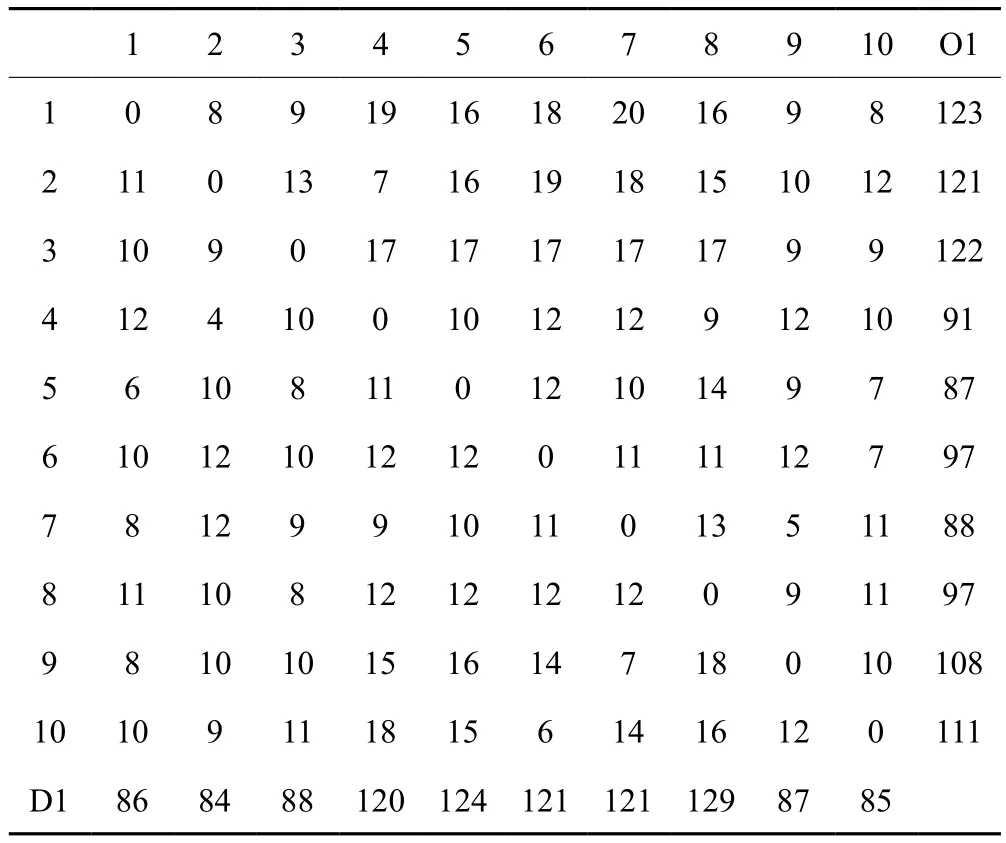
表2 时段1公共自行车租借需求Tab.2 Period 1 public bicycle rental demand

各个租赁点之间的距离以及时段2～时段6各个需求点的公共自行车租借需求从略。

3.2 算例求解

（1）相关常量取值：C=400 m，M=10 000，g=50 000元，α=15辆，f1=300元，f2=2 000元，v1=1.4 m/s，v2=5 m/s，V=2辆，p=2元/公里，r=40元，Q=100辆。

（2）根据租赁点与需求点之间的距离以及租赁点的服务半径C可得每个需求点所对应的候选租赁点，如表3所示。

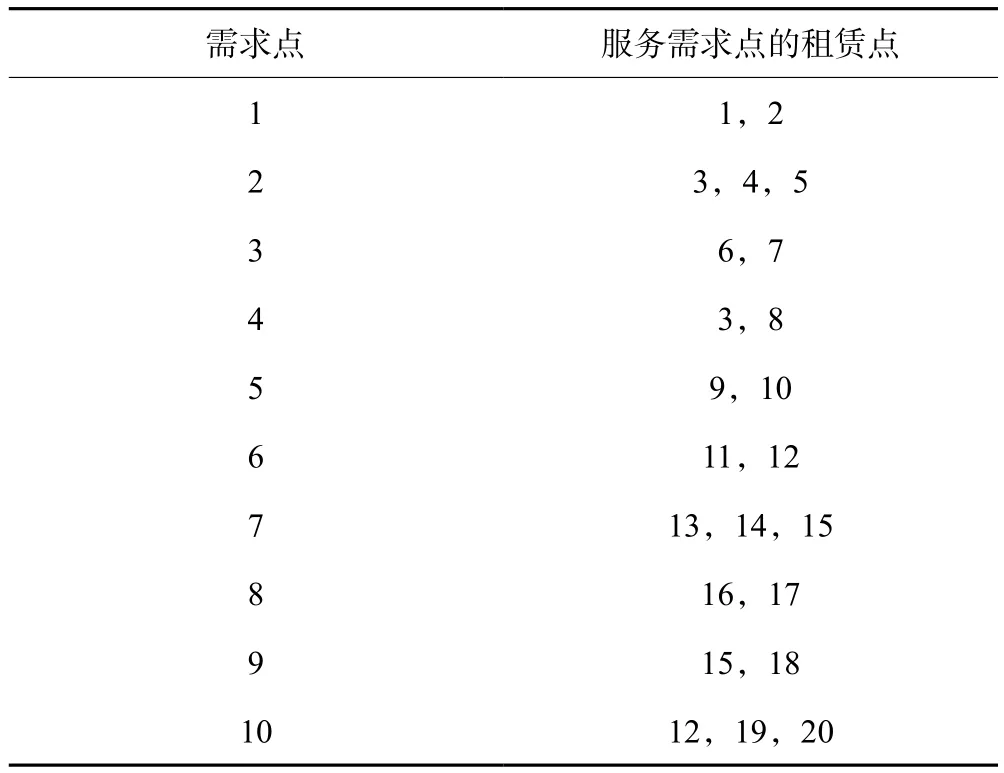
表3 需求点对应的候选租赁点Tab.3 Candidate lease points corresponding to demand points

（3）运用LINGO编程求解，运行该程序得到规划区域内居民最短的总出行时间为4 096 021秒，运输成本为363.5元，应建设的租赁点见表4，共需建设13个租赁点，在各建设的租赁点应分配的自行车数和停车桩数见表5，各租赁点各时段的调配量见表6，调度车辆运行路径为：2-4-6-7-16-17-14-18-19-20-11-8-9。

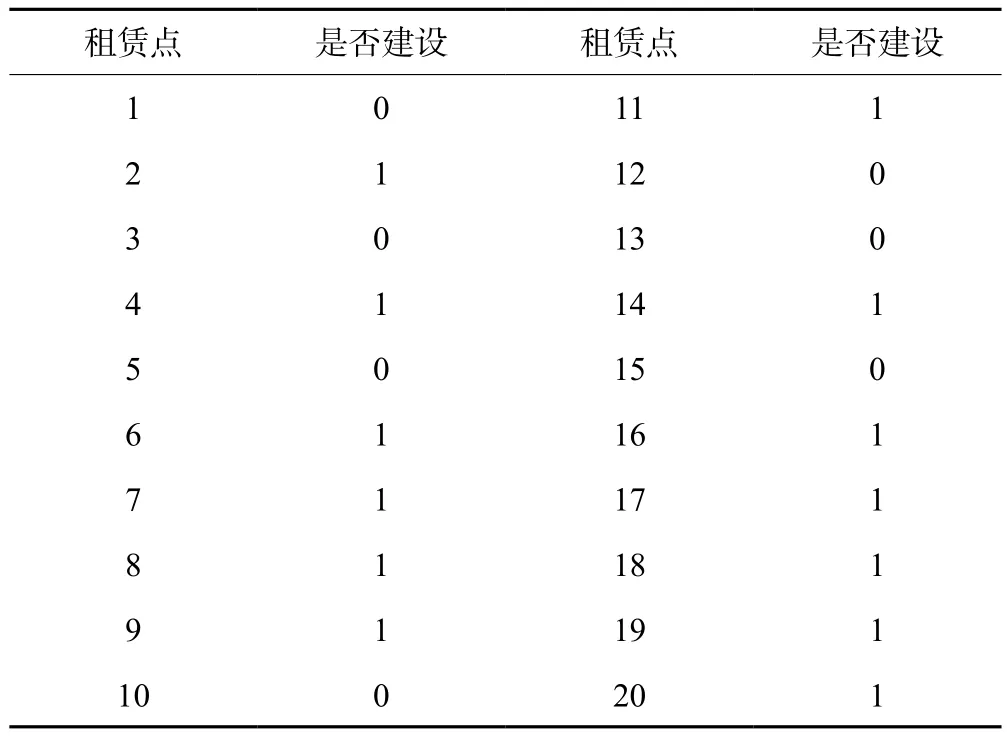
表4 系统布局方案（表中0代表不建设，1代表建设）Tab.4 System layout scheme（0 in the table represents no construction and 1 represents construction）

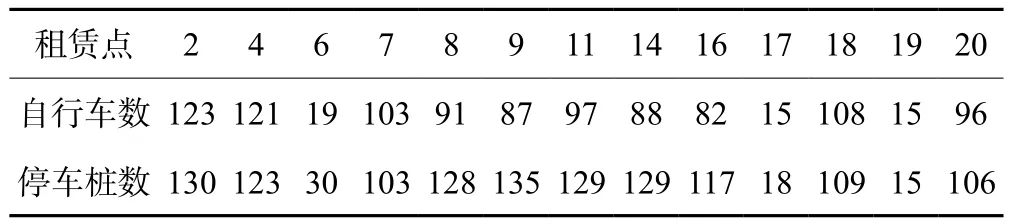
表5 租赁点分配的自行车数和停车桩数Tab.5 Number of bicycles and parking piles allocated at the rental point

表6 各租赁点各时段的调度计划Tab.6 Scheduling plan of each lease point and each period

根据以上数据可得到各建设的站点应服务的需求点和调度车辆路径，如图3所示。

图3 租赁点服务需求点图Fig.3 Service demand point diagram of rental point

4 结语

本文研究的是有调度存在的租赁点选址问题，每个时段初租赁点拥有的自行车数不受上一时段的自行车数影响，而是与本时段该租赁点服务范围内需求点的自行车出行发生量和出行吸引量有关，基于对问题的分析建立了相关的函数关系，构建了一个有调度的公共自行车租赁点选址的优化模型，并通过一个具有代表性的算例对模型进行了验证。公共自行车系统的布局应该减少对周围交通的负面影响，所以在进一步地研究时应把这些因素考虑进去。