中外规范钢筋混凝土桥梁裂缝计算对比研究

糜径超 郑 平 姚永丁

(中国电建集团华东勘测设计研究院有限公司 杭州 311122)

自上世纪30年代以来，中外学者对混凝土结构裂缝宽度进行了大量的研究并提出了各种计算理论和方法，但至今未形成一个统一的观点。目前传播较为广泛的有以下4个理论：①黏结-滑移理论；②黏结-无滑移理论；③滑移-无滑移综合理论；④数理统计理论。由于裂缝的形成及发展机理较为复杂，上述前3种理论均存在一定的局限性，世界各国在其规范编制的过程中均结合本国经验对其采用的计算理论进行了修正，最终逐渐形成两大类计算公式：半理论半经验公式、数理统计公式。

本文通过选择具有代表性国家或地区的规范，对其裂缝宽度wc计算或控制方法进行分析研究，从计算公式、裂缝宽度影响因素、裂缝宽度限值3个方面，研究不同裂缝计算或控制方法的特点，从而掌握不同地理环境、荷载条件、主观意识情况下，裂缝宽度设计的侧重点。

1 各国研究现状及计算理论

1.1 中国规范 JTG 3362-2018

该规范[1]采用数理统计理论，公式如式(1)。

(1)

该公式仅考虑构件的垂直裂缝，不包括施工中混凝土收缩过大、养护不当及渗入氯盐过多等引起的其他非受力裂缝，其允许的最大裂缝宽度为0.2 mm。

1.2 美国规范AASHTO LRFD-9th：2020

该规范[2]不直接进行裂缝宽度的计算，而是通过控制钢筋间距来控制裂缝宽度。以第一类暴露条件下，裂缝最大允许宽度为0.432 mm；第二类暴露条件下，裂缝最大允许宽度为0.216 mm为最低要求，确定钢筋间距。该钢筋间距公式依据Frosch RJ推荐的最大裂缝公式得出。R.J.Frosch RJ依据黏结-无滑移理论并结合实验数据得到的公式如式(2)。

(2)

1.3 欧洲规范EN 1992-2：2005

该规范[3]以滑移-无滑移理论为基础，结合经验得到公式如式(3)。

wc=Sr,max(εsm-εcm)

(3)

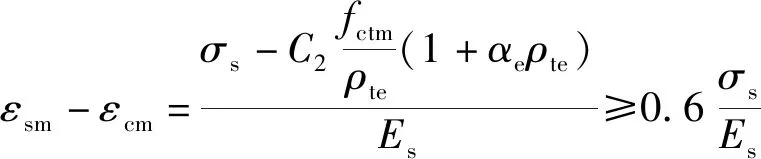
Sr,max=

式中:fctm为混凝土受拉强度平均值；k1为常数，由国家附录指定，推荐值为3.4；k2为常数，由国家附录指定，推荐值为0.425；αe为钢筋与混凝土弹性模量比。

其允许的最大裂缝宽度为0.3 mm。同时考虑该裂缝宽度计算公式较为复杂，规范还给出了免除计算的条件。

1.4 以色列规范 SI 466-1：2003

该规范[4]以黏结-滑移理论为基础，公式如式(4)。

wc=k3εsmSrm

(4)

式中：k3为使用条件调整系数；

其中：k4为钢筋黏附性能系数；σsr为截面开裂前纵向受拉钢筋应力。

式(4)适用于轴心受拉、受弯构件，允许的最大裂缝宽度为0.3 mm。同时考虑到该裂缝宽度计算公式较为复杂，规范也给出了免除计算的条件。

1.5 俄罗斯规范СНиП 2.05.03-84*

该规范[5]采用数理统计理论，公式如式(5)。

(5)

式中：

其中：Ar为有效受拉区面积；n为受拉钢筋数量。

1.6 日本规范JGC-777：2017

日本《道路桥示方书》采用的是容许应力法[6]，通过限制钢筋应力及构造措施保证混凝土裂缝宽度在可接受范围内。仅在《混凝土标准示方书》[7]中给出了裂缝计算公式，该规范采用数理统计理论，其允许的最大裂缝宽度为0.005c(mm)，其公式如式(6)。

(6)

1.7 澳大利亚规范AS 5100.5：2017

该规范[8]不直接进行裂缝宽度的计算，通过构造要求限制裂缝宽度：①受拉钢筋最低配筋率满足要求；②受拉钢筋保护层厚度不大于100 mm，且小于最大钢筋直径一半的钢筋应该忽略，受拉钢筋间距小于300 mm，T、L形断面受拉钢筋应配置在有效宽度内；③主要受拉构件：受拉钢筋最大应力应小于规范要求；④主要受弯构件：受拉钢筋直径不大于规范要求，受拉钢筋间距小于规范要求，且小于最大钢筋直径一半的钢筋应该忽略。

不同国家采用的度量单位不同，为了便于比较，以上公式的单位均已统一为N·mm。式中未标明符号含义如下：σs为开裂截面受拉钢筋应力；Es为受拉钢筋弹性模量；s为受拉钢筋间距；c为受拉钢筋混凝土保护层厚度；d为受拉钢筋直径；ρte为受拉钢筋的有效配筋率；C1为钢筋表面形状系数；C2为长期效应影响系数；C3为与构件受力性质有关的系数；h为截面高度。上述符号各国间取值有所不同，除特别说明外，本文分析均根据各国规范要求取值。

2 不同规范中的裂缝计算宽度影响因子

统计上述各裂缝计算宽度影响因子见表1，由于其中澳大利亚规范不直接计算裂缝宽度，故认为裂缝宽度构造要求为其控制因素。由表1可知，欧洲规范考虑的因子最多，其次为日本和以色列规范，俄罗斯规范考虑的因子最少。日本的《混凝土标准示方书》是少数考虑混凝土收缩徐变对裂缝影响的规范之一。其中开裂截面受拉钢筋应力、受拉钢筋混凝土保护层厚度、受拉钢筋直径、钢筋间距、受拉钢筋有效配筋率为考虑较多的影响因子。

表1 不同规范裂缝计算宽度影响因子统计

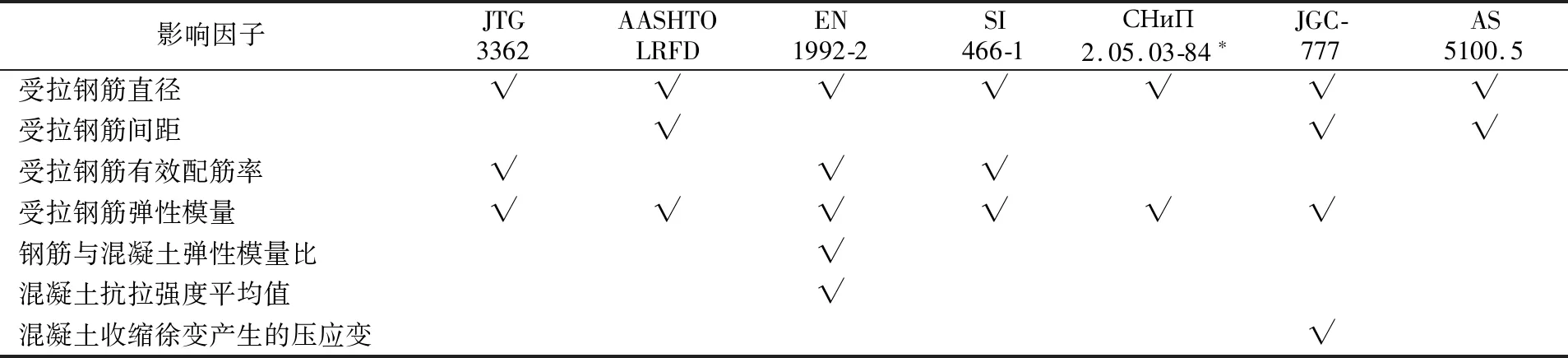
续表1

3 裂缝宽度计算结果对比分析

考虑到钢筋混凝土材料出现时间较早，各国对其材料性能和生产掌握较为充分，此处认为其生产水平在各国间差距有限，或者可以通过进口材料以保证质量。而由于不同国家所处地理位置不同、国内交通运输荷载不同、国内民众对裂缝容忍度的差别等，使得裂缝宽度计算有较大差异，因此在对比上述影响因子时存在侧重点。

各国公式纳入考虑的影响因子中：①使用条件调整系数、钢筋黏附性能系数、混凝土特性系数、多层受拉钢筋影响系数、钢筋与混凝土弹性模量比、混凝土抗拉强度平均值6类为个别国家规范采用；②钢筋表面形状系数、长期效应影响系数、与构件受力性质有关的系数3类在现有材料生产水平及钢筋混凝土桥梁使用条件的限制下，数值可变性较小；③对裂缝宽度有影响的混凝土收缩徐变产生的压应变仅在日本规范中考虑。以上影响因子均采用国家规范规定的数值，不进行控制变量对比。

假设裂缝计算条件如下：①计算对象为钢筋混凝土矩形受弯简支梁；②非控制变量影响因子取值见表2，控制变量影响因子取值见表3；③使用环境均为标准大气环境，结构仅受混凝土碳化影响；④受拉钢筋按2层布置考虑，选用带肋钢筋，无防腐涂层；⑤混凝土采用中国制造标准下C50混凝土，钢材选用中国制造标准下HRB400，性能参数根据各国规范规定计算。

表2 非控制变量影响因子取值

表3 控制变量影响因子取值

3.1 受拉钢筋应力对裂缝宽度影响

受拉钢筋应力对裂缝宽度影响见图1，由图1可见，各国裂缝公式计算得出的裂缝宽度与钢筋应力成正比，除俄罗斯规范以外，其余公式钢筋应力在90～170 MPa范围时，计算裂缝宽度基本吻合，可见俄罗斯规范计算较为宽松，为最大计算宽度的42%～48%。

图1 受拉钢筋应力对裂缝宽度影响

3.2 荷载对裂缝宽度影响

图2为活恒比取值为1.0时，裂缝计算宽度随恒载标准值变化的情况。

图2 荷载对裂缝宽度影响

由图2可见，由于各国使用状态荷载组合系数的区别，相同荷载标准值下，计算裂缝宽度区别较大，其中：中、美两国规范计算值较为吻合，最大值超出最小值3.1%左右。以色列规范计算较为宽松，为最大计算宽度的13%～43%。

由图1和图2对比可见，在其他条件不变，考虑钢筋应力和荷载组合影响下，日本最为保守。以色列、欧洲规范由于不考虑活载对裂缝宽度的影响，其计算裂缝宽度相对来说反而较为宽松。

3.3 受拉钢筋直径对裂缝宽度影响

受拉钢筋直径对裂缝宽度影响见图3。

图3 受拉钢筋直径对裂缝宽度影响

由图3可知，在上述变量控制对比方法下，钢筋直径变化对以色列规范影响最大，最大裂缝宽度增幅达到88%；其次为美国规范，增幅达到12%；其他规范受直径影响变化不大。

3.4 受拉钢筋间距对裂缝宽度影响

受拉钢筋间距对裂缝宽度影响见图4。由图4可知，当钢筋间距大于160 mm时，以色列规范的裂缝计算宽度失真严重，裂缝宽度随着钢筋间距的增加基本呈线性增长。而俄罗斯规范裂缝宽度计算值偏小。

图4 受拉钢筋间距对裂缝宽度影响

3.5 受拉钢筋保护层厚度对裂缝宽度影响

受拉钢筋保护层厚度对裂缝宽度影响见图5。

图5 受拉钢筋保护层厚度对裂缝宽度影响

由图5可知，保护层厚度变化对日本、欧洲、中国规范中裂缝宽度计算值影响较为接近，最大值超出最小值5.4%～11.9%。当保护层厚度在20～50 mm范围内变化时，除俄罗斯规范外，其余规范计算裂缝宽度基本吻合；俄罗斯规范计算裂缝宽度受保护层厚度影响较小，保护层厚度在20～90 mm范围内增幅仅为13%。

3.6 裂缝宽度主观耐受度对比

由于不同国家或地区人们对裂缝宽度的容忍程度不同，因此各国对裂缝宽度限值取值也不尽相同，裂缝宽度主观耐受度对比见图 6。

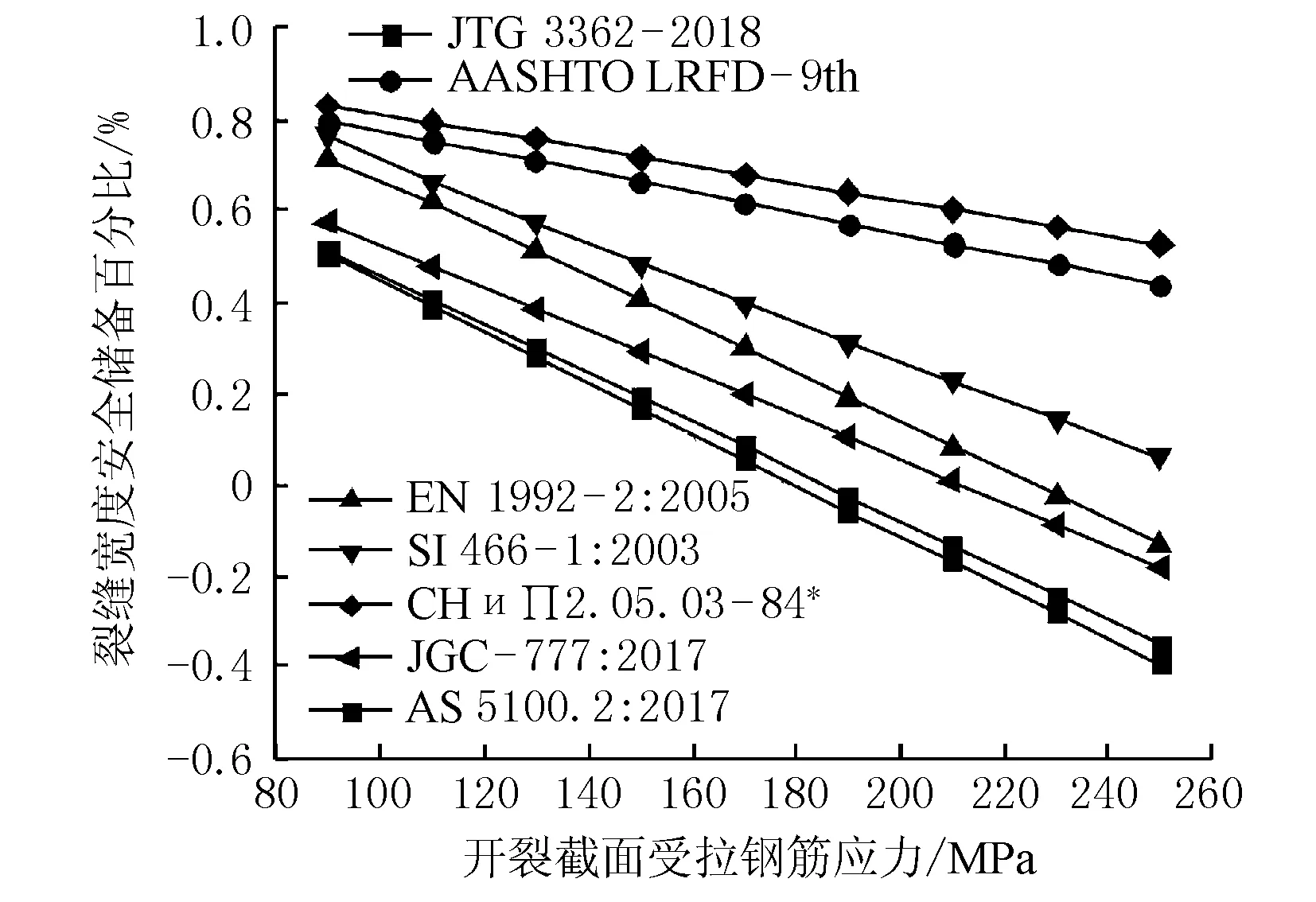
图6 裂缝宽度主观耐受度对比

由图6可知，中国、澳洲规范规定的裂缝计算要求最严格，俄罗斯、美国规范规定最为宽松。

4 结论

1) 各国裂缝公式计算得出的裂缝宽度与钢筋应力成正比，在其他条件不变，考虑钢筋应力和荷载组合影响下，JGC-777:2017公式最为保守。SI 466-1:2003、EN 1992-2:2005 2本规范由于不考虑活载对裂缝宽度的影响，其计算裂缝宽度相对来说反而较为宽松。

2) 裂缝宽度随着钢筋间距的增加基本呈线性增长，当钢筋间距大于160 mm时，SI 466-1:2003规范的裂缝计算宽度失真严重。

3) 保护层厚度变化对JGC-777:2017、EN 1992-2:2005、JTG 3362:2018规范中裂缝宽度计算值影响较为接近，最大值超出最小值5.4%～11.9%。

4) СНиП 2.05.03-84*规范下，裂缝宽度计算值较其他规范偏小。

5) 从裂缝宽度安全储备的角度分析，JTG 3362-2018、AS 5100.5:2017规范规定的裂缝计算要求最严格，СНиП 2.05.03-84*、AASHTO LRFD-9th规范规定最为宽松。