无线电能传输磁耦合机构磁心解析模型与设计方法

陈雨晨 陈凯楠 郑树轩 赵争鸣

无线电能传输磁耦合机构磁心解析模型与设计方法

陈雨晨 陈凯楠 郑树轩 赵争鸣

（清华大学电机工程与应用电子技术系，北京 100084）

本文研究含平板型磁心的磁耦合机构磁心厚度对电感的影响，建立磁心厚度对电感影响的解析模型。基于作者团队在前期研究中的等效磁路划分与磁阻计算，本文给出磁心磁阻的计算公式，对比之前不考虑磁心磁阻的磁路模型，给出新的考虑磁心磁阻的磁路，得到磁心厚度对电感的解析模型。结合线圈电流计算磁心临界饱和的厚度，给出磁心厚度设计下限。有限元仿真研究表明，本文提出的模型与有限元仿真结果吻合。根据该模型结合双LCC电路拓扑进行优化设计，最终制作出一台3.3kW的无线电能传输样机，其传输功率和效率均满足设计要求，验证了该设计优化方法的正确性和适用性。

无线电能传输；磁耦合机构；电感解析计算；LCC电路

0 引言

在无线电能传输（wireless power transfer, WPT）系统中，磁耦合机构功率密度是一个重要的性能指标。磁耦合机构的质量很大一部分来源于铁氧体磁心的质量，同时磁心的几何尺寸对线圈电感也有影响，因此在设计优化磁耦合机构的过程中，需要重点考虑磁心的几何尺寸。

为了使无线电能传输系统尽可能高效率地工作，磁耦合机构的设计至关重要[1]。文献[2]分析金属屏蔽、磁性材料屏蔽、主动屏蔽的磁耦合机构的优缺点，指出采用磁性材料可以显著增强耦合性能，提高系统效率。文献[3]对大功率轨道无线电能传输进行研究，提出一种L型线圈配合T型磁心的结构，但是没有对磁心进行尽限优化。现有研究对磁耦合机构中磁心厚度的定量优化考虑较少，且有一定的局限性，传统方式通常借助有限元仿真结合经验进行磁心设计[4-5]，但由于有限元计算速度较慢，其设计优化效率尚有较大的提升空间。在磁阻计算方面，文献[6]给出一些形状较为规则的空气的磁阻计算公式。J. Acero考虑有限厚度磁体情况下两线圈自感互感的情况，给出两层介质之间的多匝平面线圈等效阻抗的解析解和通解[7-8]，但是计算过程极为繁琐，不便于工程应用。在磁路优化方面，文献[9]对磁耦合机构的磁路磁阻进行初步探索，但是没有考虑磁心的影响，无法对含有磁心的磁耦合机构进行分析。文献[9]还分析了电磁屏蔽的结构，对比了金属屏蔽、磁材料屏蔽。

在磁心磁饱和设计方面，文献[10]使用Maxwell方程组计算含有单侧磁心的磁耦合机构的空间磁通密度，不足之处在于不能用于计算磁心的磁饱和问题。文献[11]提出一种基于有限元仿真的DD（double D-type）结构的磁耦合机构设计方法，但是对磁心的优化局限于有限元仿真，效率较低。文献[12]对现有的软磁材料的特性进行分析，但是并未提出一种针对具体磁耦合机构的磁材料厚度设计方法。文献[13]介绍铁氧体磁性材料在无线电能传输系统中的作用，以及材料电磁参数及结构形式对系统特性的影响。文献[14]使用有限元仿真的方法定性研究磁材料对电感参数的影响。上述文献均依赖有限元仿真，且结合工程经验进行磁耦合机构设计和优 化[15]，效率低下。

由此可见，磁耦合机构的经验优化设计已有一定的工程基础，但往往依赖有限元仿真和裕量设计，效率相对较低且缺乏理论依据。作者团队在前期研究中基于等效磁路划分与磁阻计算，建立了一套含平板型磁心的典型磁耦合机构电感解析模型，可基于其几何参数直接解析计算得到其自感、互感参数，计算精度已经仿真和实验验证，而计算速度远高于有限元仿真[16]。但上述模型采用磁心磁导率无穷大、磁心无磁阻的假设，无法对磁心本身进行尽限优化。本文在上述研究基础上，进一步针对磁心磁阻、磁心中的磁通密度等因素进行分析，提出相应的解析计算方法，进而使上述模型完善，可针对磁心厚度、磁饱和程度等条件进行优化。最后结合双LCC电路拓扑[17]，给出一个典型的无线电能传输系统主电路元件选型和磁耦合机构几何参数的快速优化算例，验证本文方法的有效性。

1 基于理想化磁心假设的磁阻计算模型

本文依然沿用等效磁路的研究思路，为保证叙述完整性，本节首先简要给出基于磁心磁导率无穷大假设的若干结论[16]。

本文研究的平板型磁耦合机构模型如图1所示[18]，由两块方形铁氧体磁心和两个同轴平面螺旋形线圈构成。它由14个几何参数惟一确定，见表1。

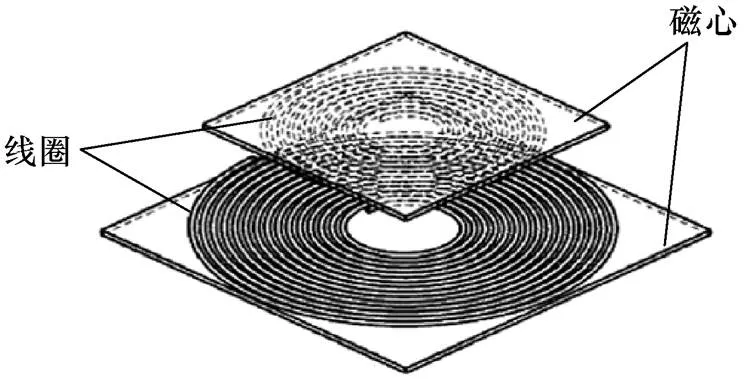
图1 平板型磁耦合机构模型

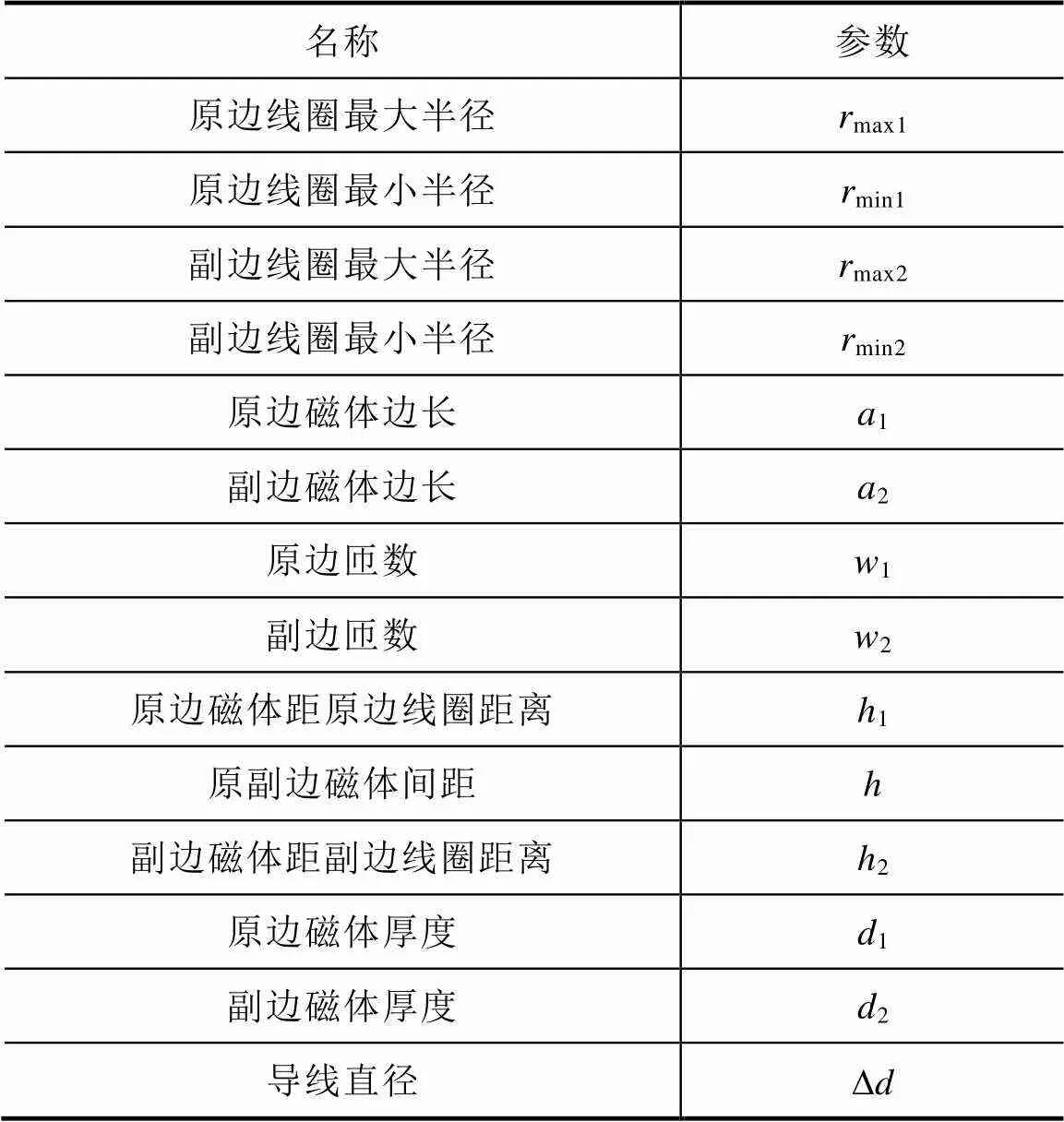
表1 磁耦合机构几何参数

文献[16]实现了对上述磁耦合机构电感的快速求解，即式（1）所示的函数映射。

其中完成磁耦合机构电感参数计算的重要桥梁就是磁阻和对应电感的关系。但是上述模型是基于理想导磁体的导磁率无穷大的假设，并没有对磁心厚度1、2进行研究。

磁心对电感的影响等价于磁心对电感所对应磁阻的影响。因此需要研究电感对应的磁阻，进而得到磁阻对电感的影响。

磁路的欧姆定律有

式中，为线圈匝数。

又有电感和磁通的关系为

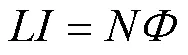
可得

磁阻主要分为空气磁阻和磁心磁阻，在磁心厚度较厚的时候磁心磁阻远小于空气磁阻，可以忽略，但是在磁心厚度较薄的时候，磁心磁阻不可忽略，磁心厚度会对电感有影响。其中空气磁阻已经在文献[16]进行了研究，但是并未充分考虑磁心磁阻对电感的影响。

为叙述完整性，先简单叙述空气磁阻的计算方法。要计算磁耦合机构空气磁阻，需要对磁通进行划分。

对一个典型的磁耦合机构截面磁通密度进行有限元仿真如图2所示。

图2 磁耦合机构截面磁通密度有限元仿真

磁耦合机构截面磁通及几何参数示意图如图3所示。

图3 磁耦合机构截面磁通示意图

主要磁通的区域划分如图4所示，包括MF、MP、L三部分，其中MF为全耦合磁通，MP为部分耦合磁通，L为漏磁磁通。

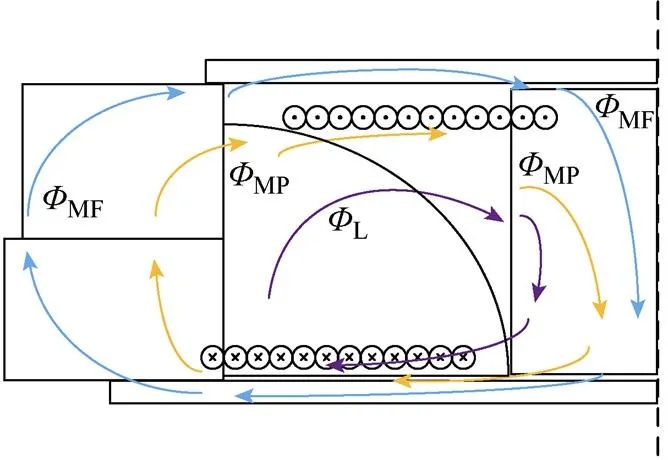
图4 主要磁通的区域划分

磁通磁路如图5所示，对应图4中的MF、MP、L三部分磁通，有m1、m2、mx、m0四个磁阻，其中m1为受到原边磁心影响的空气磁阻，m2为受到副边磁心影响的空气磁阻，mx为漏磁磁阻，m0为内部中心磁阻。

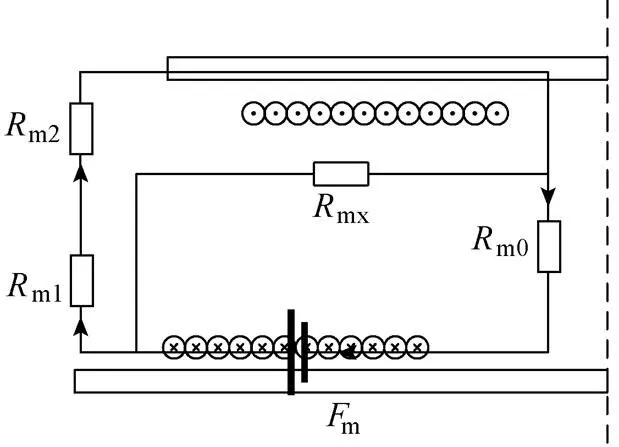
图5 磁通磁路

设

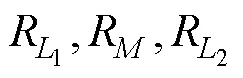
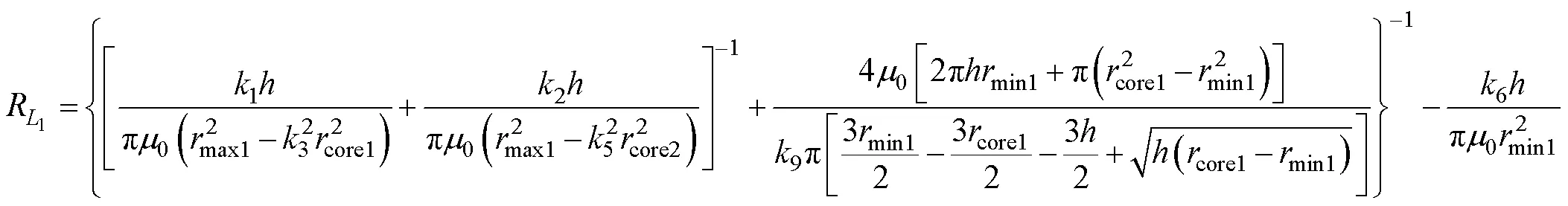
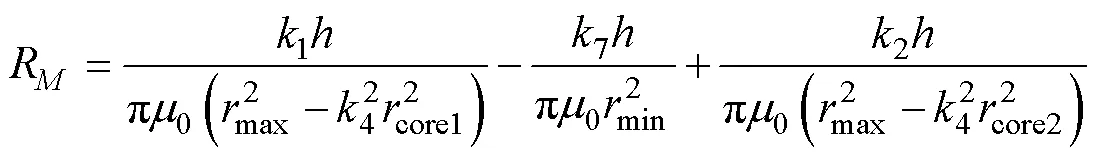
设1,2为方形磁心的边长，core1,core2为方形磁心的外接圆半径，有

空气磁阻公式是根据磁路划分、磁阻计算得到的结果，在这里不具体展开。

令

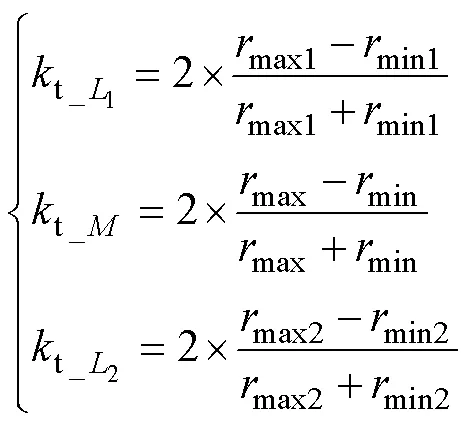
则待定系数给定为

磁耦合机构空气磁阻求解公式的适用范围为

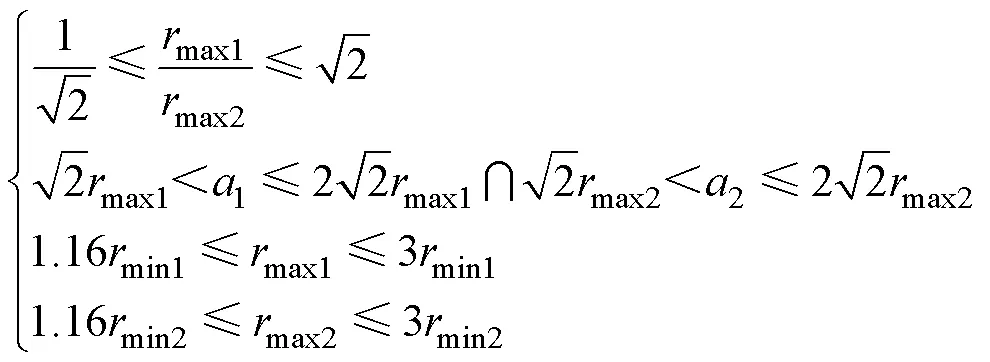
2 磁耦合机构磁心的磁阻计算方法

2.1 磁阻与电感的关系

第1节中图5的磁阻磁路[16]中未考虑磁心厚度对电感的影响，忽略了磁心磁阻。现在考虑磁心厚度对磁心的影响，来对磁心厚度进行设计优化。

考虑磁耦合机构磁心磁阻的影响，得到新的磁通划分和磁路如图6所示，与图5相比增加了磁心磁阻mf1和mf2，磁心磁阻串联在原磁路中，构成新的磁路连接关系。

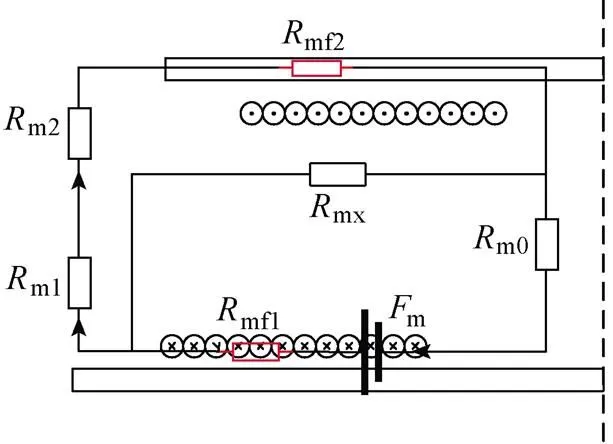
图6 磁通划分和磁路

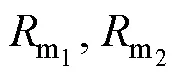
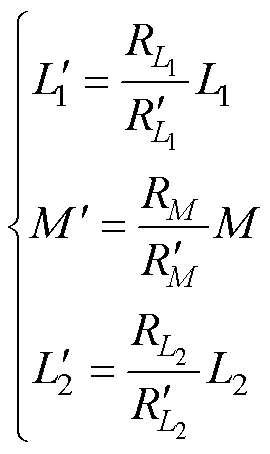
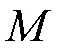
设新的磁路连接方式为

互感磁阻表达式为

2.2 磁心磁阻的计算

磁心磁阻mf1,mf2可以看作外径分别为core1,core2，内径为min1,min2，厚度为1,2的圆柱体，积分可得磁心磁阻mf1,mf2表达式为

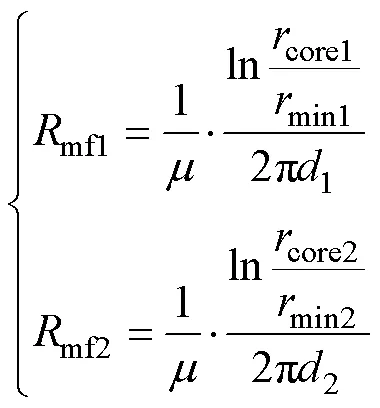
采用PC95材料的相对磁导率，设

电感参数与对应的磁阻成反比，根据新的磁阻连接关系式（14）、式（15）和式（16），结合磁心磁阻计算公式（17），即可根据式（13）计算磁心厚度变化的时候对应的新的电感值。

2.3 磁心磁通饱和计算方法

第2.1节和2.2节得出了磁耦合机构电感随着磁心厚度变化的解析模型，但是并未考虑线圈通过大电流导致磁通饱和的问题。本节结合磁耦合机构磁阻计算公式计算磁心未达到磁饱和的临界厚度，来作为磁心厚度是否在有效区间的判断条件。

根据式（2），为磁通，m为磁通对应的磁阻，磁动势这个公式通常用于截面几何尺寸可以被忽略的情况，在磁耦合机构中，圆形平面线圈的截面宽度不可被忽略，进一步由于磁通没有和所有的导线交联≠p（p为原边线圈匝数），因此不可直接使用公式。

式（2）和式（3）中均含有不确定的常数，消去求解，可得

式中：为原边或副边导线峰值电流；为原边或副边自感；m为对应的磁阻。,m可以由解析模型[16]计算得到。

以原边磁心为例，由

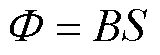
可得截面平均磁通密度为

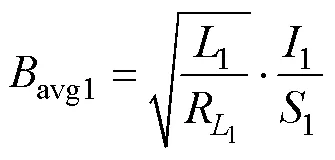
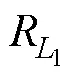
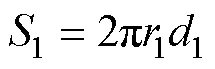
式中：1为原边磁心磁通密度最大的地方的底部圆半径；1为原边磁心厚度。有限元仿真发现，磁心截面磁场最大的地方位于线圈中部，设

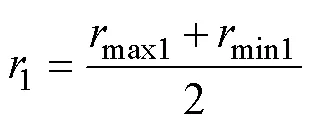
PC95材料在不同温度下的饱和磁通密度见表2，其中s为饱和磁通密度。

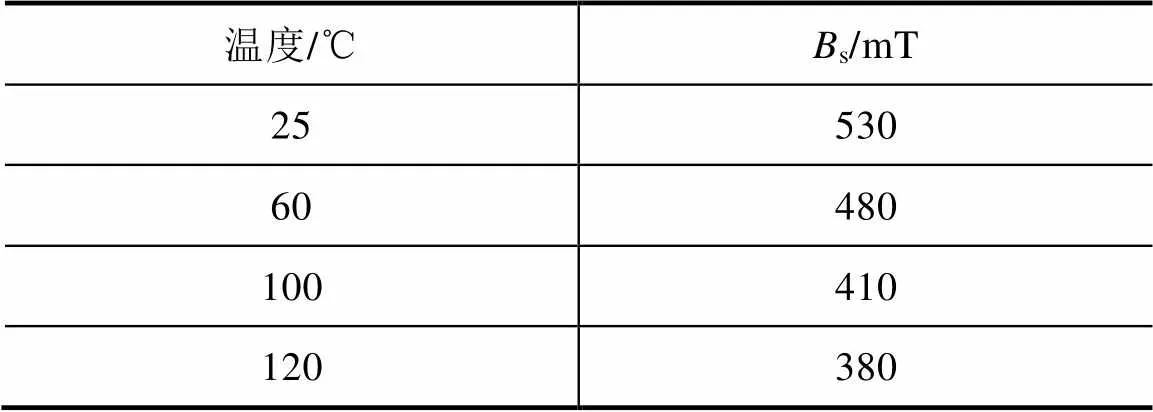
表2 PC95材料在不同温度下的饱和磁通密度（H=1 194A/m）

要求磁心磁通不饱和，即

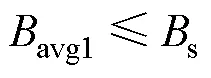
可得

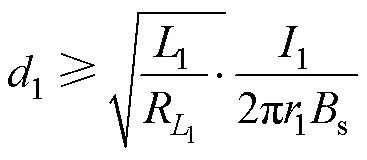
即可计算得到磁心饱和的最小磁心厚度。

3 基于磁耦合机构电感解析模型的LCC电路优化设计典型流程

3.1 磁耦合机构的设计

本文以优化3.3kW样机为例，其传输距离不小于20cm、系统效率不低于90%。谐振频率85kHz。输入350V直流，输出350V直流。磁耦合机构横向偏移10cm以内可以保证稳定的功率输出。

典型的LCC谐振电路如图7所示[17]。

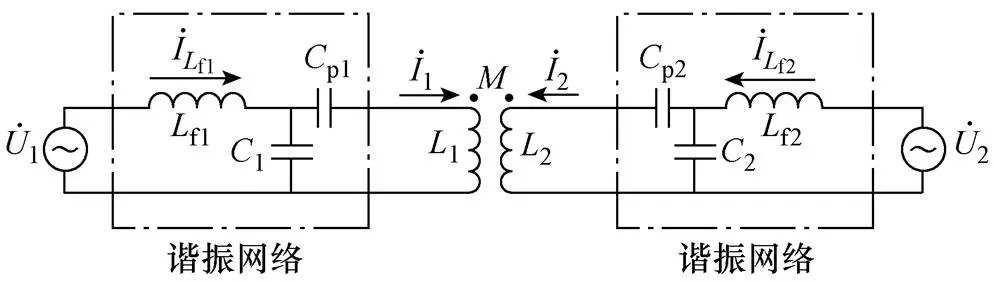
图7 LCC谐振电路

根据电路分析，得到最大功率表达式为

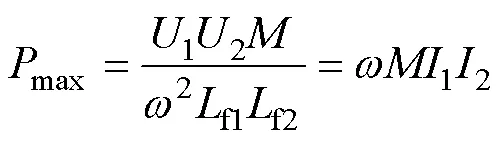
要求发射端和接收端电感参数对称，有1=2，记为，则表达式变为

由此可以根据最大传输功率3.3kW、原副边电流设计值20A，计算出互感的最小取值，有

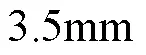
为了让线圈尽可能大以提高耦合系数，需要在磁心尺寸一定的情况下尽量将线圈做大。设线圈最大半径距离磁体边沿10mm，以便于机加工。线圈距离磁体距离1=2=6.3mm，便于机加工线圈衬底。磁体间距选=240mm，对应磁耦合机构原边上表面到副边下表面传输距离为200mm。

根据电路谐振拓扑及最大传输功率的要求，选取

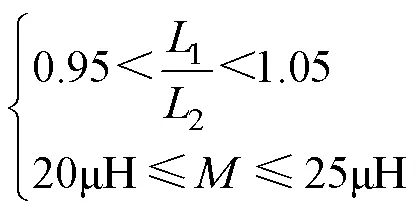
其中几何参数遍历的范围为：①原边磁心边长1从350mm间隔10mm到450mm；②副边磁心边长2从300mm间隔10mm到400mm；③原边匝数1从10匝到20匝；④副边匝数2从12匝到25匝。总计遍历18 634组样本点，Matlab耗时2 986s。最终选取出223组待选样本点，再选取1＞2,1＜2且/较大的点（为原副边线圈导线线长）以满足抗偏移需求，同时获得较大的传输效率。

最终选定几何参数组合为

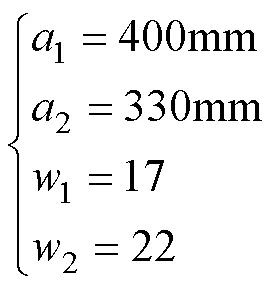
解析计算电感值为

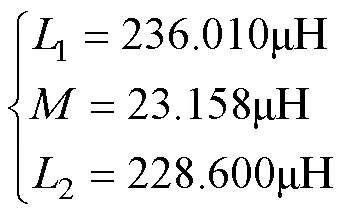
有限元仿真得到的电感值为

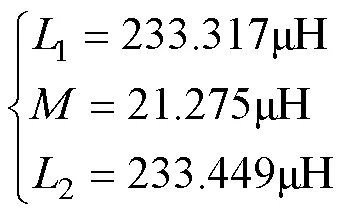
根据有限元仿真得到的实际电感值，代入式（13）～式（18）计算磁心厚度对电感的影响，结合实际可选的磁心厚度进行合理选取，最终确定满足工程实际需求的磁耦合机构样机几何参数。本次结合供应商提供的可选磁心，选取5mm厚度的PC95铁氧体磁心。

该组几何参数满足工程需求，实现了磁耦合机构的快速设计。

3.2 谐振拓扑元件参数设计

根据磁耦合机构的互感值，计算集中电感f1,f2为

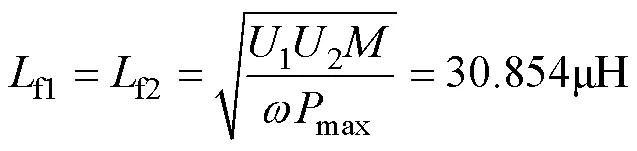
隔直电容p1,p2的值为

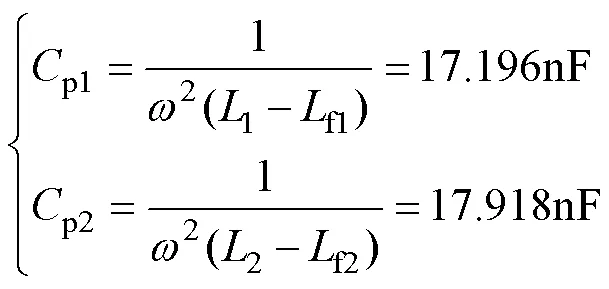
它们承受的最大电压为

谐振电容1,2的值为

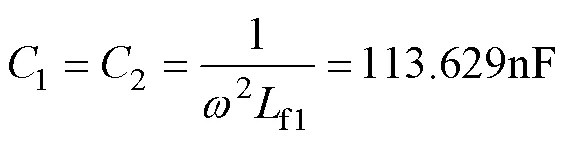
它们承受的最大电压为

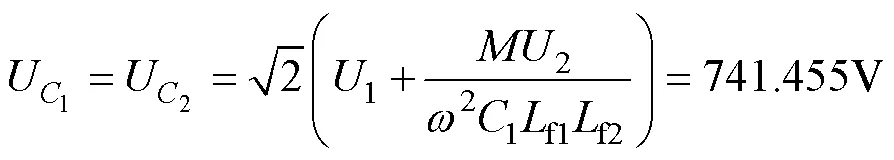
谐振拓扑设计参数见表3。

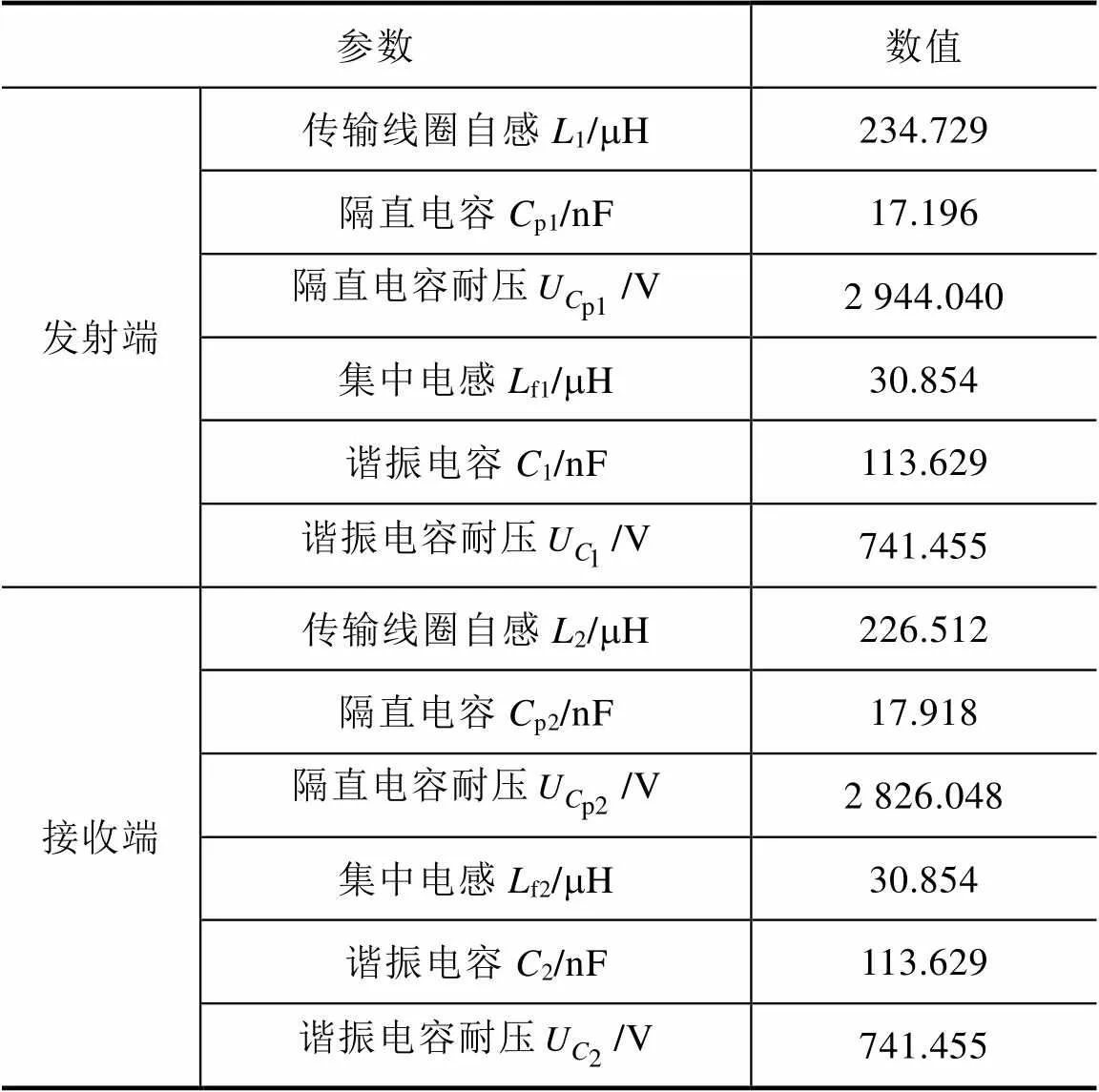
表3 设计参数

磁耦合机构的几何参数见表4。

按照上述步骤即可简洁高效地设计LCC谐振电路元件与磁耦合机构的电感和几何参数。

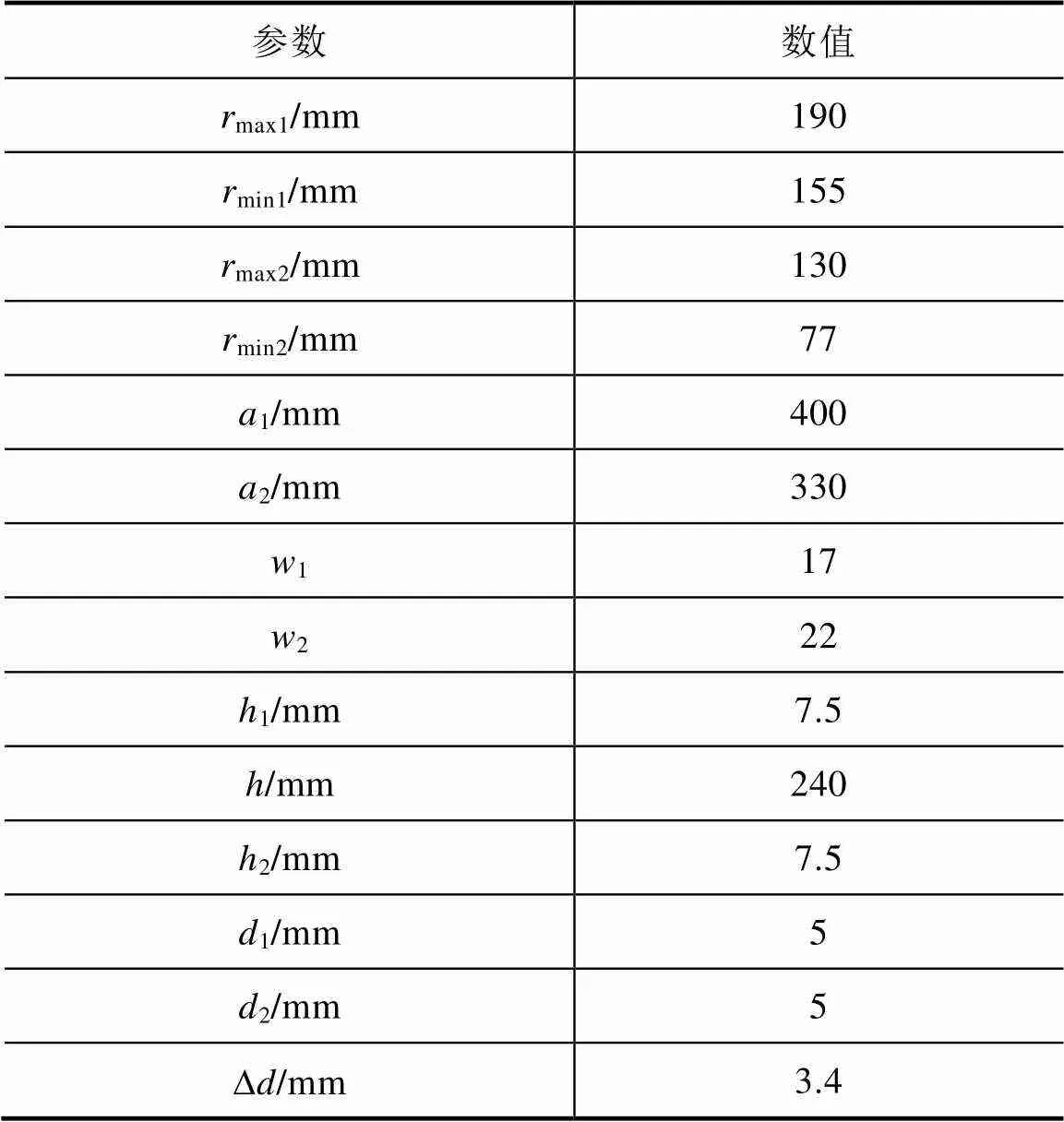
表4 磁耦合机构几何参数

3.3 磁心厚度解析模型的仿真分析

对表4的磁耦合机构使用Ansys Maxwell进行有限元仿真，对原边磁心厚度和副边磁心厚度参数扫描，以验证第2节图6提出的考虑磁心磁阻的新的磁路连接和式（13）～式（18）的正确性。仿真值与计算值的对比如图8和图9所示。

由此可以看出，磁心变薄的时候由于磁心磁阻变大，导致对应的电感值变小。所提出的磁心磁阻模型可以描述磁心厚度对电感的影响，可以应用于指导磁耦合机构的优化设计。磁耦合机构的电感会受到磁心厚度的影响。

3.4 磁心饱和磁通验证

在表4给出的几何参数组合下，选取s=480mT，1=2=20A。根据第2.3节提出的磁心饱和磁通计算方法，计算得到原副边磁心允许的最薄的厚度为

图8 原边磁心厚度变化对电感的影响

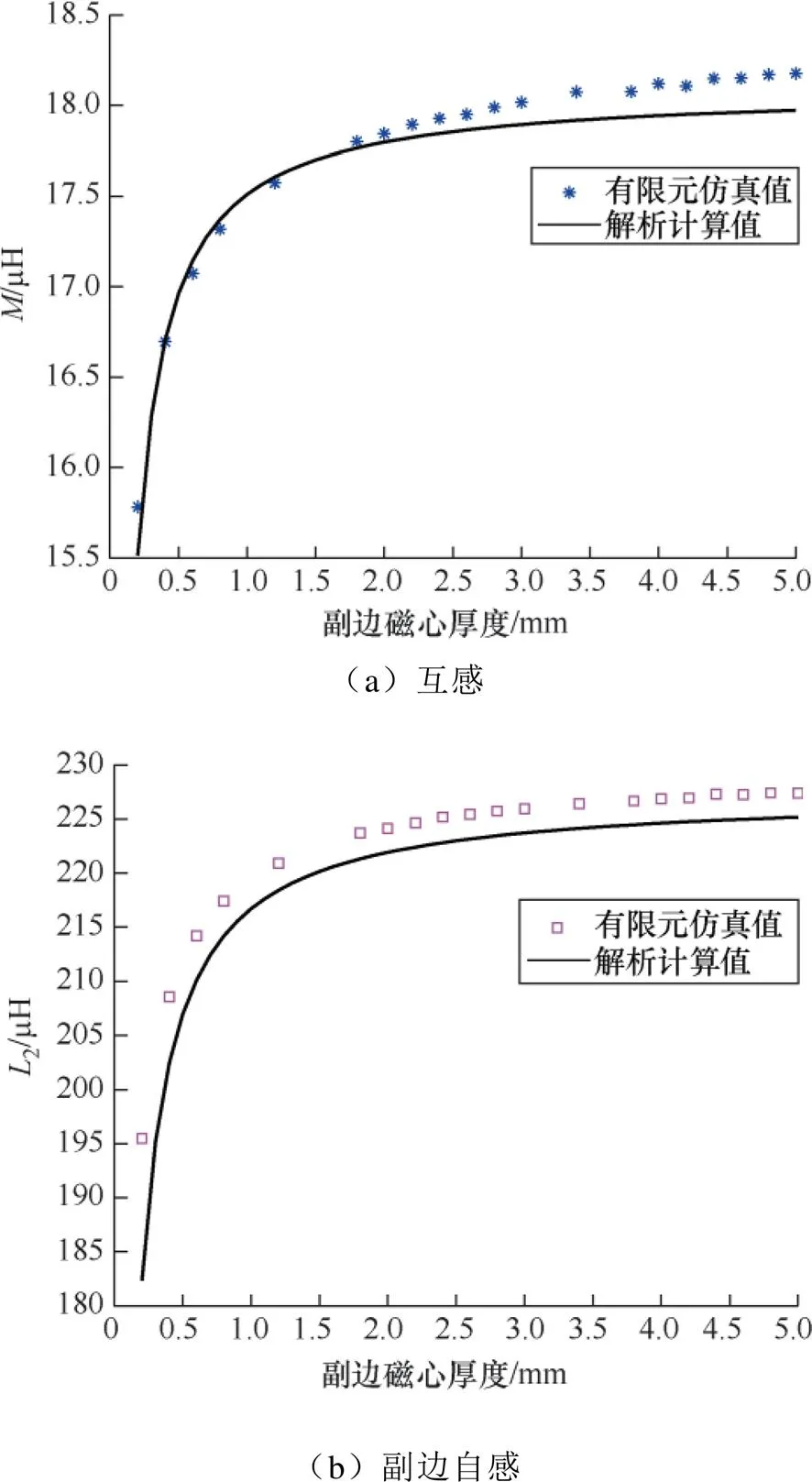
图9 副边磁心厚度变化对电感的影响

在原副边磁心厚度低于上述最薄厚度的时候，会导致磁心饱和，磁材料进入非线性区。

使用有限元仿真进行验证，得到磁耦合机构截面磁通密度如图10所示。

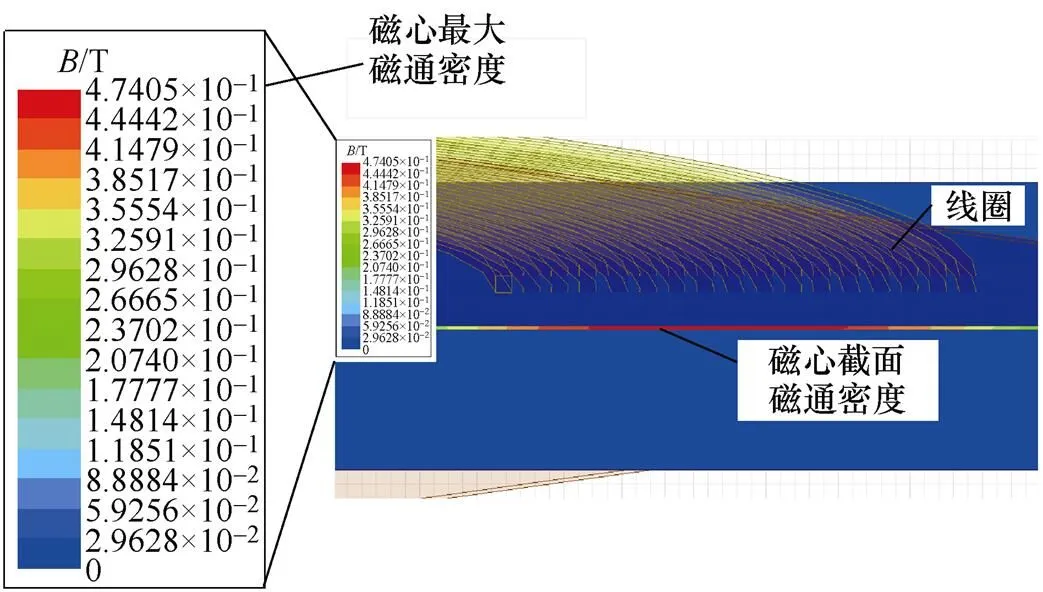
图10 磁耦合机构截面磁通密度

根据图10有限元仿真可以看出，在上述的几何条件下，最大磁通密度为

max＜s，满足设计要求。

4 实验样机满功率运行工况

对实验样机进行功率环实验，实验样机如图11所示。其中磁耦合机构用20cm高度的泡沫块进行支撑。谐振电容和电感均为定制。实验方式为功率环，原边内移相角拉满，副边不控整流。

图11 3.3kW实验样机

在达到3.3kW额定功率的情况下，样机工况如图12所示。

图12 额定功率工况

额定功率工况下，输入输出的端口波形和H桥输出波形如图13所示。

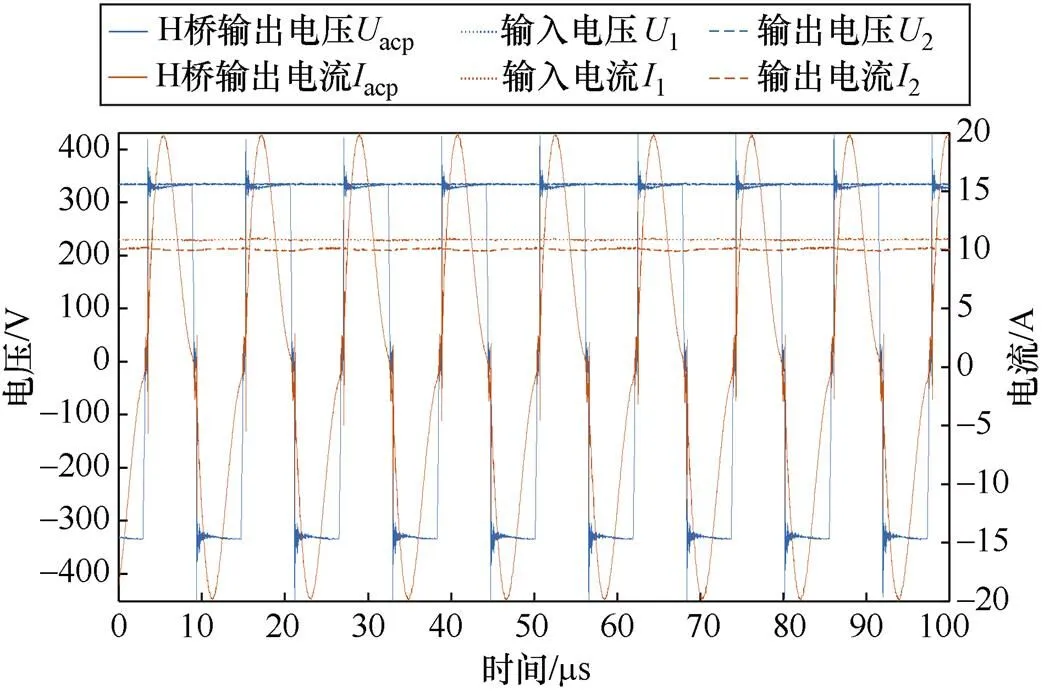
图13 额定功率工况下的波形

在样机传输功率达到额定功率3.3kW的情况下，输入电压1=334.05V，输入电流1=10.888A，输入功率1=3.637kW，输出电压2=333.87V，输出电流2=10.075A，输出功率2=3.364kW，谐振频率13=84.743kHz，整机效率1=92.475%。输出功率满足3.3kW传输要求。

在达到350V额定电压的情况下，样机工况如图14所示。

图14 额定电压工况

额定电压工况下，输入输出的端口波形和H桥输出波形如图15所示。

图15 额定电压工况下的波形

在样机达到额定电压的情况下，其中输入电压1=352.06V，输入电流1=11.525A，输入功率1= 4.057kW，输出电压2=352.01V，输出电流2= 10.640A，输出功率2=3.745kW，谐振频率13= 84.743kHz，整机效率1=92.308%。

两种工况下整机系统传输效率均达到了92%以上，传输功率高于3.3kW，满足设计要求。

5 结论

本文基于含有平板铁氧体磁心的电感解析模型，给出了考虑磁心厚度的电感解析计算模型。基于磁阻模型，计算了磁心最大磁通，得到了磁心不饱和的临界厚度值，并用有限元仿真进行了验证。结合双LCC电路谐振拓扑，给出了一种典型的双LCC电路谐振元件参数的设计流程，对磁耦合机构几何参数及电路参数进行了快速设计。最终制作出了满足设计要求的3.3kW无线电能传输样机进行满功率实验，在额定功率和额定电压的两种传输工况下，均能达到高于92%的传输效率，且传输功率高于3.3kW，表明根据该设计优化方法所设计的样机能够满足实际工程需要，证明了该方法的正确性。

[1] 王松岑, 韩秀. 磁耦合谐振式无线充电系统双边LCC补偿网络参数设计方法研究[J]. 电气技术, 2019, 20(6): 12-16.

[2] 李阳, 石少博, 刘雪莉, 等. 磁场耦合式无线电能传输耦合机构综述[J]. 电工技术学报, 2021, 36(增刊2): 389-403.

[3] 王汉丰, 唐春森, 左志平, 等. 电动车无线供电系统多负载模式分析及导轨结构优化设计[J]. 电气技术, 2019, 20(8): 6-10.

[4] 余成波, 伍雪冰, 龙曦. 基于铁芯和铝板的屏蔽线圈结构设计与仿真[J]. 重庆理工大学学报(自然科学), 2020, 34(11): 164-170.

[5] ZENG H, LIU Z Z, CHEN H X, et al. Optimization of unipolar magnetic couplers for EV wireless power chargers[C]//2016 Internatioanl Conference on New Energy and Future Energy System, Beijing, China, 2016.

[6] 赵修科. 开关电源中的磁性元件[M]. 沈阳: 辽宁科学技术出版社, 2014.

[7] ACERO J, CARRETERO C, LOPE I, et al. Analysis of the mutual inductance of planar-lumped inductive power transfer systems[J]. IEEE Transactions on Indu- strial Electronics, 2013, 60(1): 410-420.

[8] ACERO J, ALONSO R, BARRAGAN L A, et al. Modeling of planar spiral inductors between two multilayer media for induction heating applications[J]. IEEE Transactions on Magnetics, 2006, 42(11): 3719- 3729.

[9] 夏晨阳, 孙跃, 贾娜, 等. 耦合磁共振电能传输系统磁路机构参数优化[J]. 电工技术学报, 2012, 27(11): 139-145.

[10] 李中启, 李晶, 全倡辉, 等. 无线电能传输系统带磁屏蔽任意位置矩形线圈的互感计算[J/OL]. 电工技术学报, https://doi.org/10.19595/j.cnki.1000-6753.tces. 211293.

[11] 王智慧, 胡超, 孙跃, 等. 基于输出能效特性的IPT系统磁耦合机构设计[J]. 电工技术学报, 2015, 30(19): 26-31.

[12] 杜瑞华, 雷国莉, 王凌峰, 等. 电磁感应式无线供电用软磁片研究进展[J]. 磁性材料及器件, 2020, 51(2): 58-63.

[13] 冯则坤, 王鲜, 聂彦, 等. 无线电能传输系统中的铁氧体磁性材料[J]. 磁性材料及器件, 2019, 50(2): 57-64.

[14] 贾媛媛. 谐振式无线电能传输系统磁耦合机构的分析及优化设计[D]. 北京: 北京交通大学, 2018.

[15] 胡超. 电动汽车无线供电电磁耦合机构能效特性及优化方法研究[D]. 重庆: 重庆大学, 2015.

[16] 陈雨晨, 陈凯楠, 赵争鸣, 等. 一种用于无线电能传输系统的磁耦合机构的电感计算方法: 中国, CN202110974271.7[P]. 2021-12-14.

[17] 陈凯楠, 赵争鸣, 刘方, 等. 电动汽车双向无线充电系统谐振拓扑分析[J]. 电力系统自动化, 2017, 41(2): 66-72.

[18] ZENG Hao, LIU Zhizhen, HOU Yanjin, et al. Optimi- zation of magnetic core structure for wireless charging coupler[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.

Analytical model and design method of magnetic core for wireless power transfer magnetic coupler

CHEN Yuchen CHEN Kainan ZHENG Shuxuan ZHAO Zhengming

(Department of Electrical Engineering, Tsinghua University, Beijing 100084)

In this paper, the influence of the thickness of the ferrite core on the inductance of the magnetic coupler with a flat core is studied, and an analytical model of the influence of the thickness of the ferrite core on the inductance is established. Based on the equivalent magnetic circuit division and magnetoresistance calculation of the authors’ team in the previous research, this paper gives the calculation formula of the ferrite core magnetic resistance. The magnetic circuit of the resistance is obtained, and the analytical model of the thickness of the ferrite core on the inductance is obtained. Combined with the coil current, the critical saturation thickness of the ferrite core is calculated, and the design lower limit of the ferrite core thickness is given. The finite element simulation is used for verification, and the model proposed in this paper is in good agreement with the finite element simulation results. According to the model combined with the dual LCC circuit topology, the optimal design is carried out. Finally, a 3.3kW wireless power transmission prototype is made, and its transmission power and efficiency meet the design requirements, which verifies the correctness and applicability of the design optimization method.

wireless power transfer; magnetic coupler; inductance analytical calculation; LCC circuit

2022-03-21

2022-03-29

陈雨晨（1994—），男，硕士研究生，主要研究方向为电动汽车无线电能传输。

国家电网有限公司科技项目（SGHB0000KXJS1900586）