基于相似波形的漏磁检测缺陷信号小波分解及提取方法
杨 杰 李红梅 赵春田, 杨洪礼
基于相似波形的漏磁检测缺陷信号小波分解及提取方法
杨 杰1李红梅2赵春田1,2杨洪礼3
(1. 南方科技大学,广东深圳 518055;2. 四川大学,成都 610207;3. 山东科技大学,山东 青岛 266590)
漏磁检测技术被广泛应用于铁磁构件缺陷的检测和量化评估,其对缺陷形状、尺寸的三维反演成像、量化能力,尤其是对常见的自然(腐蚀、疲劳)复杂缺陷的三维成像能力,是漏磁检测技术水平的核心标志之一。由于实际缺陷形状不规则、常包含多个坑点,致使其漏磁检测信号彼此影响。为提升复杂缺陷的成像精度和数据处理速度,从漏磁信号里自动分解并剥离出对应缺陷的信号是很重要的前置工作。本文提出一种基于相似波形的漏磁检测缺陷信号小波分解及提取方法,用于自动分解并拾取每个缺陷的漏磁检测信号,并自动确定每个缺陷的位置及边界,以备后续利用其完成对缺陷的三维反演成像。该方法基于实际检测到的缺陷漏磁信号的形态特征,匹配与其波形最相似的小波基;用选取的小波基对每个通道的漏磁检测信号进行多尺度分解,得到每个通道信号的小波高频系数;再根据小波系数特征确定每个通道信号中存在的缺陷数量和缺陷所在的位置,并提取每个通道各处缺陷的漏磁信号;最终通过判定缺陷信号相邻通道的连通性,将所在连通区域内的缺陷信号进行集成,得到各处缺陷的信息集,从而实现对所有缺陷漏磁检测信号的提取。本文提出的方法可用于对复杂缺陷漏磁检测信号的准确和快速提取、分离和集成,为后续缺陷的三维反演成像奠定基础。
漏磁检测;相似小波基;小波分解;缺陷信号提取
0 引言
近年来,管道运输以其安全、便捷、高效等优点在石油、天然气等能源运输行业被广泛应用。截止到2020年底,我国油气长输管道里程累计达到16.9万km。相关数据表明,我国超过半数的管道已经进入服役的中后期。为避免发生管道泄漏事故和造成重大的生命财产损失,对管道进行有效的高精度完整性检测是必要的。管道漏磁内检测法具有操作简便、可靠性好、检测效果好等优势,被广泛用于对油气管道中缺陷的检测和量化。
漏磁检测[1-3]可实现对油气管道内、外表面的金属损伤、焊缝等缺陷的有效无损检测,其原理示意图如图1所示。在利用磁体对管壁进行饱和磁化的状态下,如图1(a)所示,当管壁中不存在缺陷时,磁通回路没有扰动,空气中的磁敏传感器拾取到的漏磁场不会发生畸变;如图1(b)所示,当管壁中存在缺陷时,管体中的磁力线在缺陷界面处发生折射,导致管体外空气中漏磁场信号的畸变。通过分析检测漏磁场信号是否有畸变,可实现对管体缺陷的识别;通过分析畸变漏磁场信号的形态、幅值等特征可实现对缺陷的粗略量化。在实际管道检测工程中,经常将沿管道长度方向(轴向)设定为轴,管道周向方向设定成轴,管道径向方向设置成轴(见图1)。磁敏传感器拾取的漏磁信号幅值为电压值,单位为mV。
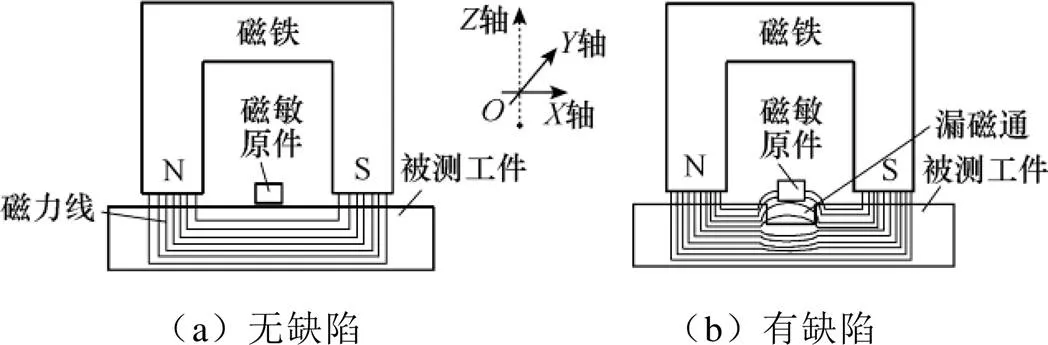
图1 漏磁检测原理示意图
近年来,随着我国装备制造能力的大幅提升,国产漏磁检测机器人的硬件装备水平与国外的差距在快速缩小,但在缺陷的量化评定精度、速度和可靠性等方面,与国外相比仍存在很多不足。仅就缺陷的量化评定能力而言,目前国内外的漏磁检测技术仍处于对缺陷的定位查找及对其尺寸的粗略量化阶段,对管道中缺陷形状的三维量化反演成像能力仍然不足。本研究团队在利用实际检测信号反演缺陷处磁荷分布规律的基础上[4],提出缺陷深度场概念,并建立缺陷三维轮廓反演的方法及算法,可实现对任意复杂缺陷的三维轮廓的反演成像[5]。以上理论创新技术已实现转化,具有广阔的工业应用前景。进一步地,为提升对缺陷的量化评定能力和处理速度,从漏磁检测信号中自动识别、分离和提取缺陷的漏磁信号是很重要的前置工作。由于实际工程缺陷形状不规则,多个坑点信号常近距离分布、或一个区域包含多个坑点缺陷,致使其漏磁检测信号彼此关联、相互影响,降低了后期缺陷识别及成像量化精度。因此,为提升漏磁检测对复杂缺陷的识别和量化成像精度,需要对上述近距离分布的多缺陷进行分解剥离和单独提取。目前应用较广泛的缺陷识别提取方法主要有幅值差分阈值法[6-7],但其对近距离分布复杂缺陷的识别提取精度不高、信号提取自动化程度低、对数据样本和人工经验的依赖性较高。即便是同一组数据,如果由不同的人员处理,其对缺陷信号的识别提取结果可能不同。因缺陷数据分析依赖人工、费时费力,导致数据分析结果常在检测完成后2~4月才能给出,严重降低了检测结果的时效性。
漏磁检测缺陷信号的提取,尤其是对相互关联的、跨越多通道的复杂缺陷信号的提取,目前还没有可适用的高效、成熟算法,不利于后续的缺陷三维反演成像及量化评定。针对以上问题,本文给出一种基于相似波形的漏磁检测缺陷信号小波分解及自动提取方法,从缺陷漏磁检测信号的波形特征出发,匹配与其波形相似度高的小波基,用其对漏磁检测信号进行多尺度分解,探究小波高频系数与缺陷信号的对应规律,从而实现对缺陷信号的自动提取。该方法不仅能提高缺陷的提取精度和处理速度,也适用于对复杂缺陷信号的剥离和提取,为后续的缺陷三维反演及量化评定奠定基础。
1 相似小波分解提取方法
1.1 小波多分辨率分析
小波分析[8-9]自20世纪70年代被提出,在信号分析及数学领域得到快速发展,很好地弥补了许多其他信号分析方法(如傅里叶分析方法)的不足,在理论和实际中都得到了广泛应用。相较于傅里叶分析方法,小波分析方法的一个显著优势是可以对信号进行局部分析。1986年,Meyer给出了一组小波,对其进行伸缩和平移可构成一组空间序列的标准化正交基,显著推动了小波的实际应用。1988年,Mallat在做小波构造研究时提出多分辨率分析[10-13]的理念,从数学定义和空间概念对正交小波[11]都进行了形象的解释和描述,并提出目前在信号去噪领域中广泛采用的算法——Mallat算法[14],使小波分析方法在理论和应用层面都实现了跨越。在小波的计算可行性问题被解决后,它的独特优势,例如可检测信号的突变点和奇异性等局部信息的能力,便显著地发挥了出来,解决了信号分析领域的诸多难题。

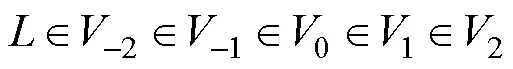
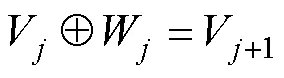

信号经小波分解后映射到不同尺度的函数空间,并得到不同尺度下相互正交的时频系数。不同的尺度对应不同的频率范围,即可实现在不同频率范围内观察信号,并获取其多频域的时频信息。另外,小波的可构造性极大提高了小波分析在实际应用中的灵活性和便捷性。
1.2 漏磁检测缺陷信号的小波提取方法
基于相似波形小波分解的漏磁检测缺陷信号提取技术路线如图2所示,本文对漏磁检测缺陷信号的提取可分解为五步:①对检测信号去噪;②选取最优小波基;③对检测信号进行小波分解;④初步锁定缺陷区域;⑤精确提取各缺陷信号。

图2 基于相似波形小波分解的漏磁检测缺陷信号提取技术路线
1)小波基的选择
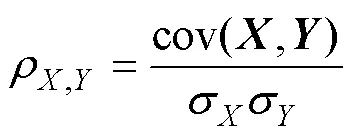

由于皮尔逊系数是对称的,两个向量的平移或尺度变化都不会影响皮尔逊系数值的变化。两个向量间的皮尔逊系数及其所对应的相关性关系见表1。
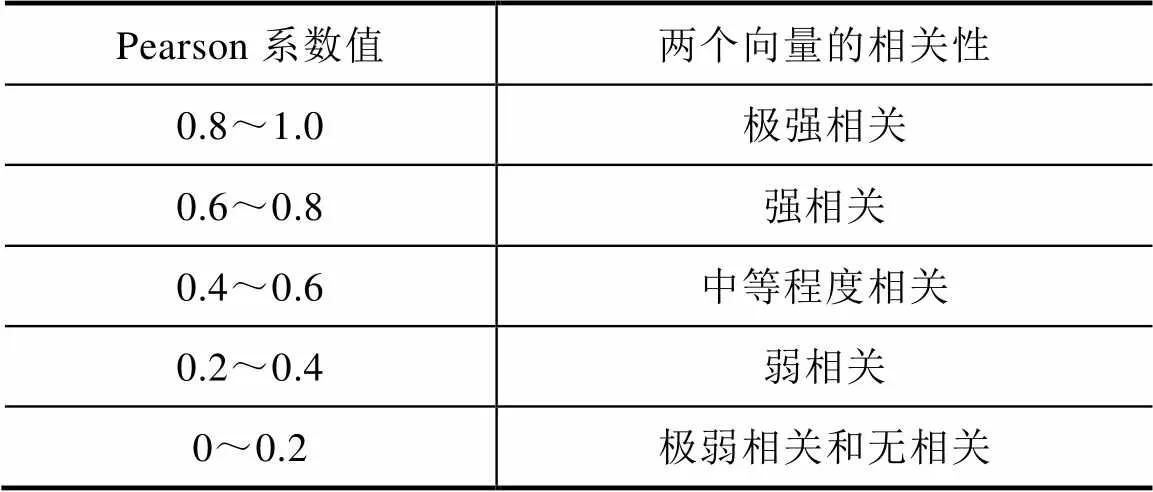
表1 Pearson系数与两个向量的相关性
由此,计算不同的小波基与漏磁检测缺陷信号的Pearson系数,选取Pearson系数值高的小波基作为对漏磁检测缺陷信号分解用的小波函数,可提升对单个缺陷识别拾取的精准度。以工程中实际获取的漏磁检测缺陷信号的径向分量为基准,本文计算了其与典型的几种小波基函数的Pearson系数,见表2。Rbio3.1小波与漏磁检测缺陷信号径向分量的Pearson系数为0.964 9,相似度较高,两者的波形相似性如图3所示。
2)缺陷信号提取
根据波形相似原则,采用Rbio3.1小波基对漏磁检测信号进行小波多尺度分解。
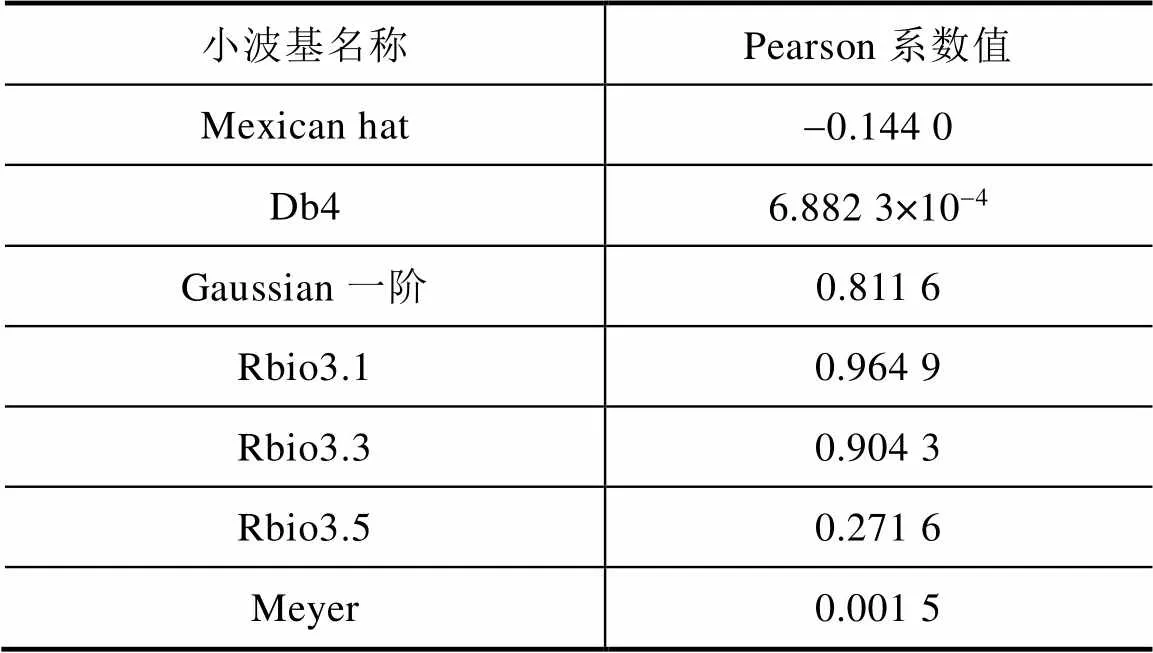
表2 不同小波基与漏磁检测缺陷信号的Pearson系数
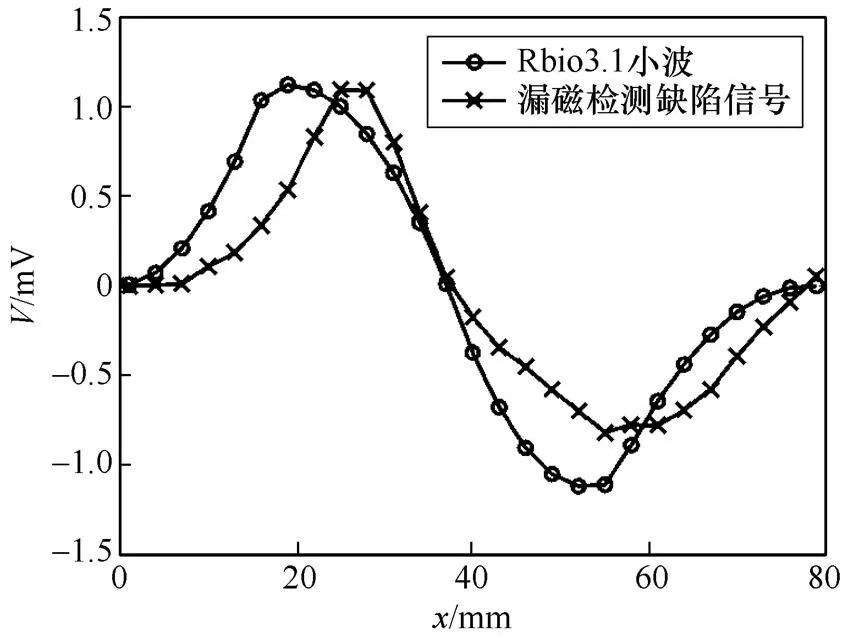
图3 Rbio3.1小波与缺陷信号径向分量的波形相似性
(1)缺陷信号的单通道分解及提取
用Rbio3.1小波对如图4(a)所示的含有单个缺陷的管道漏磁检测单通道信号做4级分解,结果如图4(b)和图4(c)所示。图4中,CA和CL(=1, 2, 3, 4)分别表示小波低频和高频系数值。由图4结果可见,高频系数CL可较好地拾取并表征缺陷信号。在无缺陷区域,CL接近于0;在有缺陷区域,CL存在1个极小负峰、2个极大正峰,单个缺陷信号经小波分解后得到的高频系数的分布规律具有惟一性,没有衍生出多余旁瓣峰,可据此对单个缺陷进行识别,有利于后续对复杂缺陷的分解和拾取。本文中,选取CL2对缺陷进行识别和提取,尺度选取原则为:
①该尺度分解得到的小波低频系数与原信号波形相似。
②该尺度分解得到的小波高频系数,在有缺陷部分能量集中、无旁瓣,在无缺陷部分的值接近于0。
③在满足①②条件下选低尺度。依据小波多尺度分解的模极大值传递规律[21],小波分解尺度越低,极大值点传递时误差越小。
依据小波变换基本理论,具有显著特征波形的信号,经小波分解后得到的系数的模极大值点,对应原信号的特征点。CL2与缺陷特征点对应关系如图5所示,用Rbio3.1小波对图5(a)所示的管道漏磁检测缺陷信号进行2级分解,得到的CL2如图5(b)所示。图5(b)中标注的模极大值点与图5(a)中标注的特征点从左到右存在一一对应的关系。因此,可先通过对CL2模极大值的拾取实现对缺陷及缺陷所在边界位置的确定,再对应出其在漏磁检测信号中的位置,从而可从原漏磁检测信号中截取出缺陷信号。
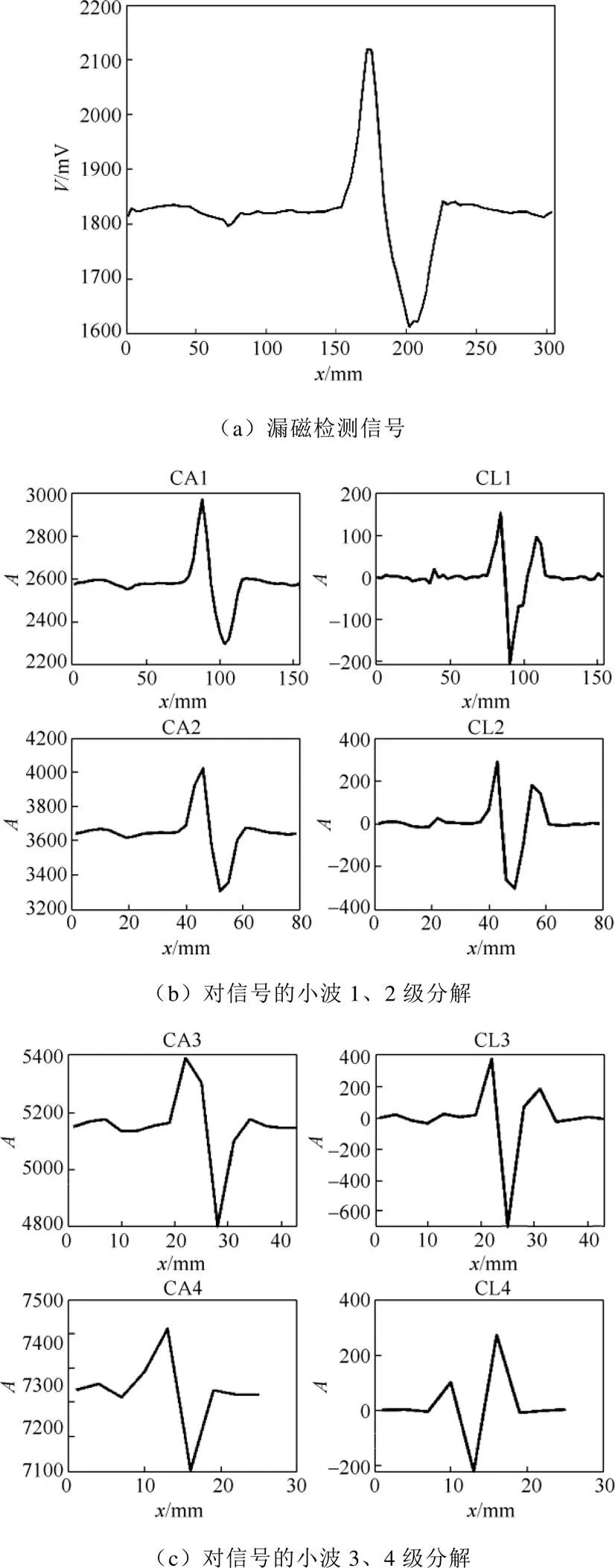
图4 对信号的小波多尺度分解结果

(a)管道漏磁检测缺陷信号
(b)信号经分解后的二尺度小波高频系数
图5 CL2与缺陷特征点对应关系
综上所述,一个具有明确特征波形的信号,选取与其特征波形相似度大的小波基,对其进行小波分解,得到与原信号对应的小波低频系数和高频系数。其中,低频系数波形与原信号波形相似,高频系数放大表征原信号中的局部细节特征信息,且高频系数的模大值点与原信号的特征点具有惟一映射关系。由此,先在小波高频系数中根据特征提取出缺陷信号,后根据其映射关系提取出其在原信号中的位置信息,从而完成缺陷漏磁信号的提取。该方法的优越性表现在,基于相似波形的小波多分辨率分析对特征信号的辨认有惟一性,可提高复杂缺陷区域中对单个缺陷的识别率,进而提高缺陷的提取精度。
漏磁检测单通道缺陷信号提取的方法步骤如下:
①对检测信号去噪。用基于Mallet算法的小波分解与重构法实现。
②小波分解并确定阈值。用Rbio3.1小波对漏磁检测信号进行二级分解,根据分解后得到的二尺度高频系数(CL2)确定阈值。经验证,非缺陷信号对应的CL2模值不超过缺陷信号对应的CL2模值的30%。由此,找到分解后得到的CL2模的最大值max,将max(∈[0.1, 0.3])作为阈值去筛取缺陷信息。
③拾取缺陷数据。选定步骤②中的,在步骤②得到的CL2中,将模值大于max的数据提取出来。
④缺陷数据分段。在步骤③得到的缺陷信息中,找到其中的局部极小值点,以极小值点为基准对缺陷信息分段。
⑤确定每个缺陷信号段的边界并截取。以每个局部极小值点所在位置为基准,向左扩散找到与其相邻的局部极大值点,将其所在位置作为缺陷左边界,将局部极小值点的位置作为缺陷右边界。为减小误差,左右边界分别向左和向右各扩散两个单位,根据模极大值传递规律,将这些位置坐标乘以4对应到原信号中的位置,截取出原信号中边界范围内的信号数据。
单通道缺陷信号提取流程如图6所示。
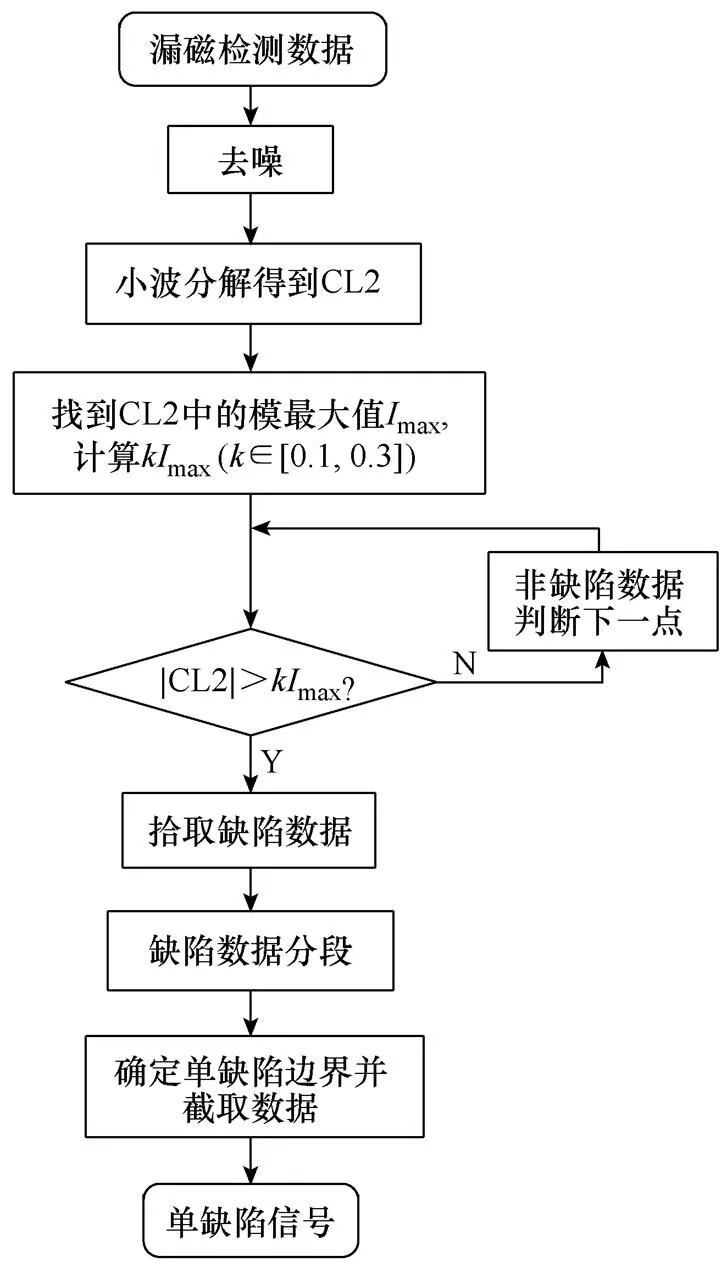
图6 单通道缺陷信号提取流程
(2)平面缺陷信号的分解和提取
基于一维单通道信号(缺陷长度方向)的缺陷提取结果,缺陷在长、宽平面内的二维完整信号的提取,主要通过对缺陷边界位置的连通性判断来实现。长、宽平面缺陷信号提取流程如图7所示,包含以下主要步骤:
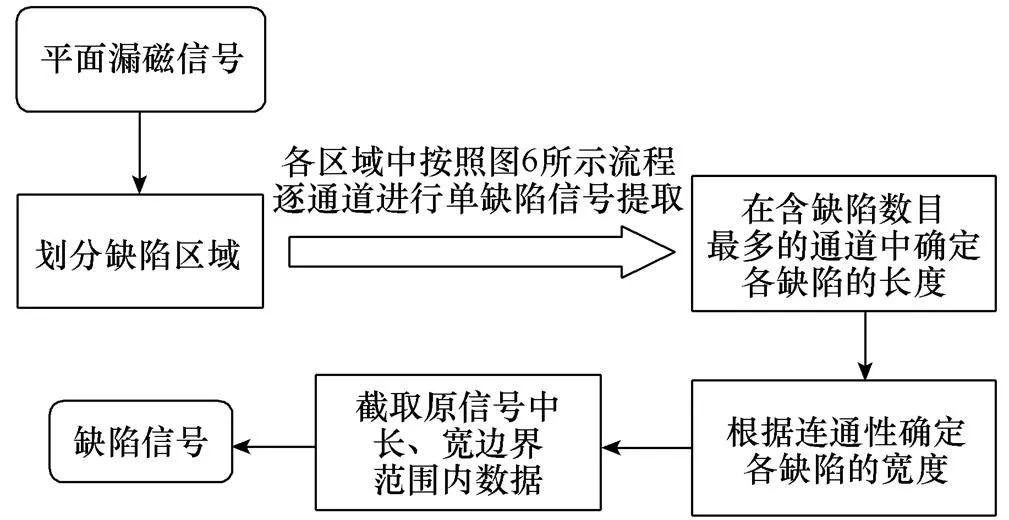
图7 长、宽平面缺陷信号提取流程
①划分缺陷区域。按照图6所示缺陷数据拾取流程,对平面漏磁信号逐通道进行缺陷识别,获取所有存在缺陷的通道。将其中具有连通性的通道划定为一个初级缺陷区域。
②在每个初级缺陷区域进行单个缺陷的剥离提取,主要步骤如下:
a)单个缺陷的提取。按照图6所示流程依次在步骤①划定的初级缺陷区域内进行每个通道内含独立缺陷的划分和提取,并记录每个独立缺陷的位置和长度。
b)独立缺陷长度的确定。在含缺陷数目最多的通道中,取各缺陷在不同通道中长度的最大值作为其长度,并记录其所在的边界位置。
c)独立缺陷宽度的确定。在步骤b)中确定的各缺陷的长度边界范围内,获取存在缺陷的通道,将其中具有连通性的通道集成为一个缺陷,其所包含的通道边界表征了缺陷的宽度,记录其位置。
d)从原漏磁检测信号中,截取出由以上步骤b)和c)中确定的缺陷长度和宽度边界位置范围内的漏磁检测数据,存储起来,完成单个缺陷的提取。
其中,本文将相邻间距小于等于2个采样单位的通道认为是具有连通性的通道。
2 缺陷提取结果验证
2.1 一维漏磁检测缺陷信号提取
为了验证上述漏磁检测缺陷信号的单通道分解与提取方法的可行性和准确度,用Matlab对实际管道漏磁检测的工程数据进行了缺陷提取。选取其中存在缺陷的300条单通道信号进行了缺陷提取验证,提取阈值系数设定为0.1。运行结果显示,本方法对其中缺陷信号的有效识别和提取率为98%,图8为其中的两组缺陷提取效果。图8(a)为内含单个缺陷,图8(b)为内含3个相邻缺陷。图8中,origin标识线为原漏磁检测信号,01、02、03标识线分别为所提取的缺陷编号。由图可见,本方法可对相邻的多个缺陷进行有效剥离和单独提取,且被提取的缺陷信号完整、无冗余信息。

图8 单通道缺陷信号的提取结果
2.2 二维平面缺陷信号的提取
为了验证上述漏磁检测缺陷平面信号提取方法的有效性,用Matlab对实际工程的管道漏磁检测信号中的缺陷二维信号进行了提取,将提取阈值系数设定为0.1。第一批测试数据内含20个缺陷,本方法自动识别和有效提取了其中的19个缺陷信号,各缺陷信号都被单独且完整地提取和保存。第二批测试数据内含50个缺陷,本方法有效识别和提取了其中的48个缺陷信号,有效提取率为96%。
图9(a)为内含3个密集缺陷的仿真漏磁检测信号。缺陷信号彼此影响,所跨越的通道范围相互覆盖。缺陷提取结果如图9(b)~图9(d)所示,3个密集缺陷都能够被单独识别并剥离提取出来。

图9 多个缺陷的二维信号提取结果
图10(a)为实际工程管道的漏磁检测信号1,内含一个长轴向缺陷。图10(b)为缺陷信号的提取结果,可见缺陷信息被完整提取且无冗余信息。图11(a)为实际工程管道的漏磁检测信号2,其内含3个形状不规则、相互影响的密集缺陷,图11(b)~图11(d)为其缺陷提取结果,可见3个缺陷的单独识别和提取效果良好。
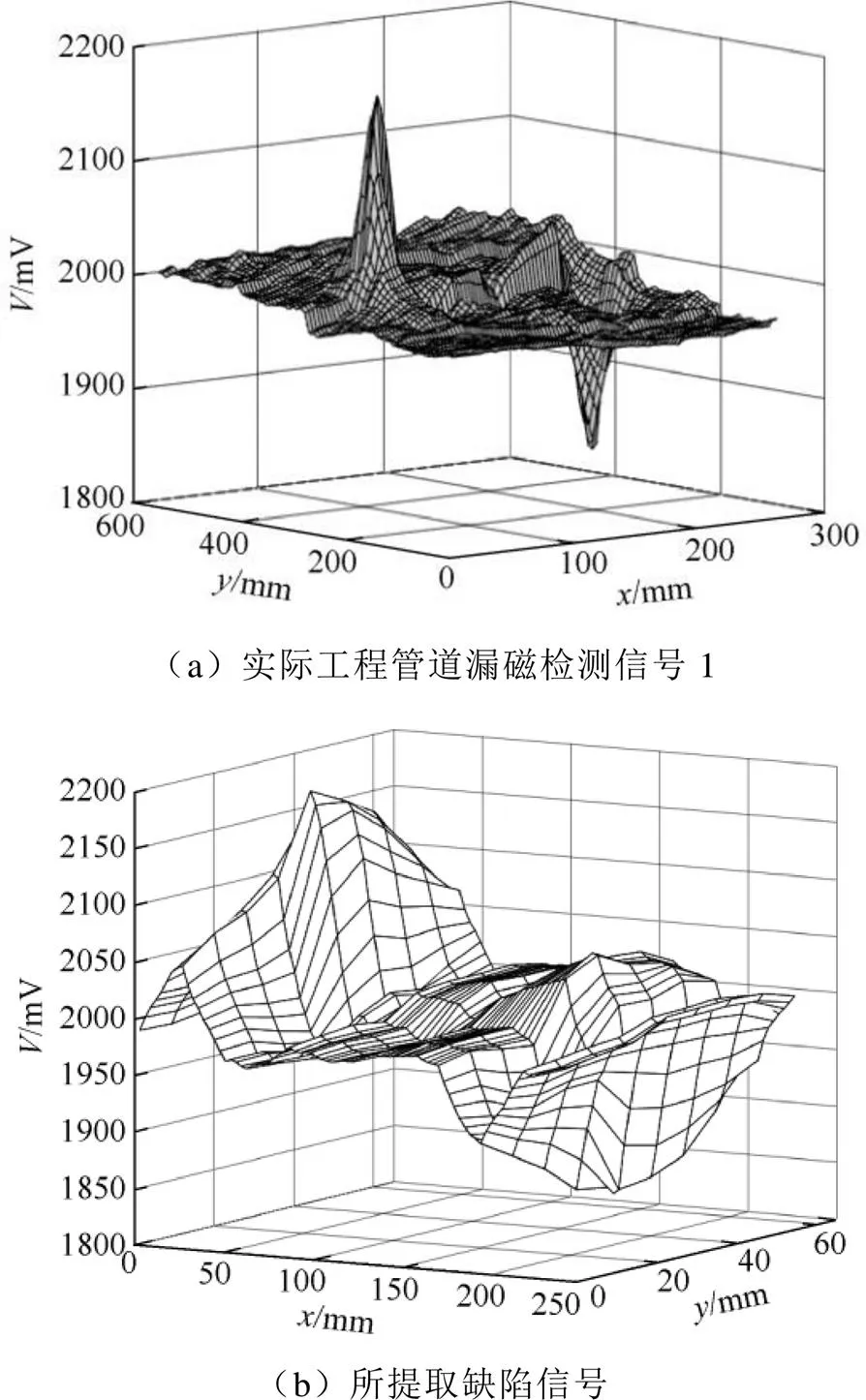
图10 工程管道漏磁检测信号1的二维缺陷提取结果
3 结论
本文基于小波多分辨率分析方法,给出了一种漏磁检测缺陷信号提取方法。本方法基于相似波形小波分解思想,经过波形相似度计算,选取了与缺陷漏磁信号相似度高的Rbio3.1小波,并应用其对实际漏磁检测信号进行了分解和提取。测试结果表明,本文方法可有效从内含多个密集缺陷的信号区域,分离和提取出单个独立的缺陷信号,并可精确地确定各缺陷所在的位置和边界,实现对相互影响的复杂缺陷进行分别识别和单独提取。本文方法的创新点及优势如下:

图11 工程管道漏磁检测信号2的二维缺陷提取结果
1)通过选取与缺陷信号波形相似度高的小波基函数对漏磁信号进行小波分解,建立了小波高频系数与单个缺陷信号的映射关系,并基于此进行缺陷识别和提取,解决了漏磁检测对密集型复杂缺陷的单独提取难题。
2)开发了漏磁检测缺陷提取算法,编写了相应的计算程序,从实际工程管道的漏磁检测数据里,提取出了96%以上的二维缺陷信号,实现了缺陷提取过程的全程自动化。
相对于现有方法,本文方法提高了对密集型复杂缺陷的分解和单独识别能力,提升了缺陷提取的准确率和速度,为随后的缺陷轮廓反演成像计算奠定了基础,在实际管道漏磁检测工程中有广泛的应用前景。
[1] 孟祥吉, 宋兵臣, 刘健, 等. 管道部件及典型缺陷漏磁内检测图像化显示研究[J]. 管道技术与设备, 2021(1): 26-32.
[2] 戴光, 吴忠义, 朱祥军, 等. 管道内外壁缺陷的漏磁检测[J]. 无损检测, 2018, 40(3): 19-23, 28.
[3] 杨理践, 耿浩, 高松巍. 长输油气管道漏磁内检测技术[J]. 仪器仪表学报, 2016, 37(8): 1736-1746.
[4] LI Hongmei, ZHANG Fuchen, YANG Bin, et al. Dis- tribution characteristics of calculated magnetic charges around discontinuous structures in magnetic memory testing[J]. International Journal of Applied Electro- magnetics and Mechanics, 2019, 59(4): 1321-1329.
[5] LI Hongmei, HUANG Ranran, ZHAO Chuntian, et al. 3D reconstructing of arbitrary defects with magnetic flux leakage testing signals[C]//2020 IEEE Far East NDT New Technology and Application Forum (FENDT), Kunming, 2020: 51-55.
[6] 王婷婷. 金属表面缺陷特征智能提取及特征分析的方法研究[D]. 沈阳: 东北大学, 2017.
[7] LI Min, LI Xue, GAO Chenxing, et al. Acoustic microscopy signal processing method for detecting near-surface defects in metal materials[J]. NDT and E International, 2019, 103: 133-140.
[8] MALLAT S G. Multiresolution approximations and wavelet orthonormal bases of L2(R)[J]. Transactions of the American Mathematical Society, 1989, 315(1): 69-87.
[9] CHUI C K. An introduction to wavelets[M]. American: Academic Press Inc., 1992.
[10] 周志昊. 基于小波变换的电力变压器直流偏磁时励磁电流研究[J]. 电气技术, 2020, 21(6): 69-72.
[11] 胡昌华, 张军波, 夏军, 等. 基于MATLAB的系统分析与设计—小波分析[M]. 西安: 西安电子科技大学出版社, 2000.
[12] 杨福生. 小波变换的工程分析与应用[M]. 北京: 北京科学出版社, 2000.
[13] 乔苏朋, 杨艳, 陈世群, 等. 光伏阵列故障检测方法综述[J]. 电气技术, 2021, 22(7): 1-6.
[14] 米正英, 王瑜, 王立东, 等. 电弧信号小波去噪分析[J]. 电气技术, 2020, 21(3): 103-107, 116.
[15] 肖迎群, 冯良贵, 何怡刚. 基于小波分形和核判别分析的模拟电路故障诊断[J]. 电工技术学报, 2012, 27(8): 230-238.
[16] 武佳卉, 邵振国, 杨少华, 等. 数据清洗在新能源功率预测中的研究综述和展望[J]. 电气技术, 2020, 21(11): 1-6.
[17] 崔芮华, 曹欢. 基于相空间重构的航空电弧故障识别方法[J]. 电工技术学报, 2020, 35(增刊1): 243- 250.
[18] 钟建林, 何友, 任献彬. 基于波形相似度的容差模拟电路软故障诊断[J]. 电工技术学报, 2012, 27(8): 222-229.
[19] 彭海. 皮尔逊相关系数应用于医学信号相关度测量[J]. 电子世界, 2017(7): 163.
[20] 陈世群, 高伟, 陈孝琪, 等. 一种基于极限学习机和皮尔逊相关系数的光伏阵列故障快速诊断方法[J].电气技术, 2021, 22(10): 57-64.
[21] 朱延功, 高学山, 刘嵩, 等. 使用小波分析方法提取焊缝位置信息[J]. 哈尔滨工业大学学报, 2001, 33(3): 389-392.
Wavelet decomposition and extraction method of defect magnetic flux leakage testing signals based on waveform similarity
YANG Jie1LI Hongmei2ZHAO Chuntian1,2YANG Hongli3
(1. Southern University of Science and Technology, Shenzhen, Guangdong 518055; 2. Sichuan University, Chengdu 610207;3. Shandong University of Science and Technology, Qingdao, Shandong 266590)
Magnetic flux leakage testing (MFLT) technology has been widely used in engineering to identify and measure defects in ferromagnetic components. Its capability in reconstructing defects in the three-dimensional (3D) form, especially for general complex defects formed naturally (such as by corrosion and/or fatigue), is one of the primary indexes representing the technological advances. Because the actual defect shape is irregular and often contains multiple pits, its magnetic flux leakage detection signals affect each other. To improve the accuracy of reconstructing defects in 3D and speed up the data processing, the prerequisite is to automatically strip off and extract the valid defect data from the MFLT signals. To effectively locate, separate, and integrate information for reconstructing each defect, a wavelet decomposition and extraction method is proposed. Based on the morphological characteristics of the MFLT signals, a wavelet basis is selected that matches the characteristics of the defect signals closely. This wavelet basis is used in the multi-scale decomposing of the MFLT signals and in the calculating of the associated wavelet high frequency coefficients. Then the wavelet coefficient is utilized in identifying and locating the defects in each channel of the signals, as well as in extracting the MFLT data corresponding to each defect. Finally, by examining the signals of each defect in a channel and integrating all the associated data in the adjacent channels, a complete set of data related to each defect is obtained. The proposed method can be applied to quickly identify, extract and integrate the MFLT data for all defects, which provides the basis for the 3D defect reconstruction.
magnetic flux leakage testing; similar wavelet basis; wavelet decomposition; defect signal extract
2022-01-06
2022-02-26
杨 杰(1997—),女,山西省大同市人,硕士研究生,主要从事数据分析与缺陷检测方面的研究工作。
深圳市科技研发资金(JCYJ20190809144809345)
四川大学人才项目(YJ202091)
中央高校基本科研基金

