计及可靠性的风光互补发电系统容量优化配比研究

宋 宇 李 涵 楚皓翔 李 斌

计及可靠性的风光互补发电系统容量优化配比研究

宋 宇 李 涵 楚皓翔 李 斌

（国网江苏省电力有限公司超高压分公司，南京 211102）

风电、光伏发电系统具有天然的波动性与随机性特点，使发电系统风险评估难度增加。本文采用序贯蒙特卡洛算法对发电系统可靠性进行研究，再以发电系统规划与运行的总费用期望等年值最小为优化目标，综合考虑可再生能源规划建设成本、可再生能源年度补贴收益、常规火电机组年度运行成本、发电系统碳市场收益及系统电量损失总成本等因素，构建计及发电系统可靠性的风光机组容量配比优化模型。最后研究典型算例IEEE-RBTS系统下风光发电容量最优配比，并在某区域电网进行仿真分析，验证了该模型的有效性。

蒙特卡洛；风光互补；可靠性；经济性

0 引言

加快发展新能源被认为是优化我国能源结构、促进生态文明建设和经济社会可持续发展的重要战略措施。在目前“双碳”目标的背景下，削减煤炭直接消费、降低煤炭在一次能源消费中占比、摆脱对煤炭的高度依赖是必然趋势[1]，而大力发展风力、光伏等新能源发电是实现该目标的重要方式。提高风电和光伏的入网水平成为发电系统发展的主要趋势，而风力、光伏发电的波动性和随机性为电力系统风险评估增加了难度[2]。

现有的风光容量规划研究思路大多是从实际运行的层面出发，结合风、光的互补特性优化系统，从而提高其运行的鲁棒性[3]。然而，该研究思路的实施往往会导致对可再生能源的过度投资，从而使整个系统的建设成本难以合理控制，造成不必要的资源浪费。

在规划期进行电力系统整体设计，能够实现在追求规划投建与实际运行全过程的经济性最优的同时，减少对可再生能源过度投资的情况，并且保证可再生能源能够被有效利用。为保证发电系统整体具有更高的经济性，一方面，要合理分配风光发电的容量比例，另一方面，要更多关注系统可靠性的约束条件。

针对发电系统机组配比的优化，目前通常的做法是利用时序仿真法[4]，其优化目标为电力系统的总效益最大化，构建考虑风、光发电出力的年度时序生产模拟的电力系统仿真模型。然后，在仿真模型的基础上，借助优化算法进行最优容量配比的 求解。

本文建立计及发电系统可靠性的风、光发电年度生产仿真模型，以发电系统规划与运行的总费用期望等年值最小为目标函数，计及可再生能源规划建设成本、可再生能源年度补贴收益、常规火电机组年度运行成本、发电系统碳市场收益及系统电量损失总成本共五个因素，将风光系统接入典型算例IEEE-RBTS系统与某区域电网进行仿真。在算例分析中，采用蒙特卡洛算法进行随机生产模拟，模拟各机组的时序出力，分析系统的建设成本、运行成本和风险损失费用，得到在实际应用中，使成本最低且效益最高的风光互补发电系统容量配比。

1 发电系统可靠性评估模型

1.1 风力发电可靠性评估模型

目前应用最为广泛的风力发电机组主要有双馈感应发电机（doubly-fed induction generator, DFIG）与永磁同步发电机（permanent magnetic synchronous generator, PMSG）[5]。就应用情况而言，永磁同步发电机相对更加适应低风速的环境，且实际运行中故障率低，本文算例中发电系统考察的风力发电机为永磁同步发电机。

计及元件故障与风速的影响，风力发电系统三状态的状态转移过程如图1所示。

图1中，A为正常工作状态；B为风力发电系统处于故障的状态；C为风力发电系统处于降额状态。s为风力发电系统正常工作时的故障率；b为风力发电系统正常工作时发生功率降额的概率；s为风力发电系统从故障状态恢复到正常状态的修复率；b为风力发电系统从降额状态恢复到正常状态的修复率。

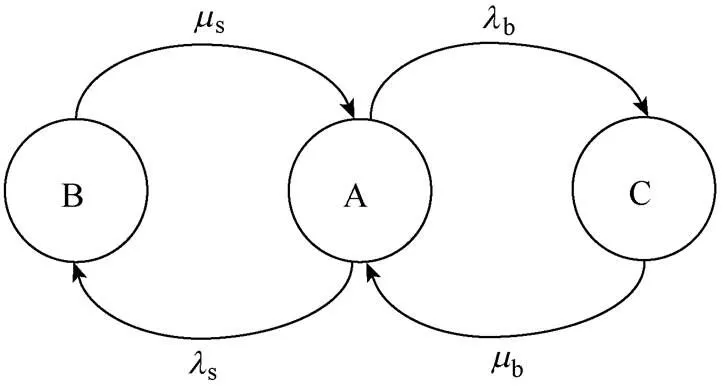
图1 风力发电系统状态转移示意图

在三状态转移模型中，风力发电系统可由正常运行状态向故障和降额两种状态进行转移[6-7]。当其处于正常状态还未进入故障状态前，正常运行持续时间AB为

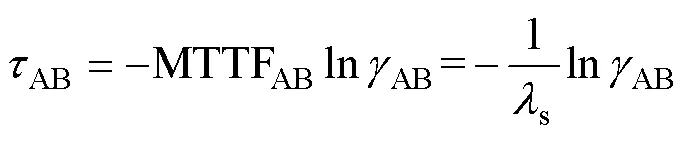
式中：AB为[0, 1]内随机数；MTTFAB为故障前平均持续时间。

当其处于正常运行状态还未进入降额状态前，正常运行的持续时间AC为

式中：AC为[0, 1]内随机数；MTTFAC为降额前平均持续时间。

风力发电系统可由故障状态、降额状态经过修复、调整进入正常运行状态，其故障状态的持续时间BA和降额运行的持续时间CA可表示为

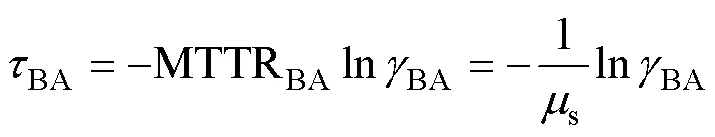
式中：BA和CA均为[0, 1]内随机数；MTTRBA和MTTRCA分别为故障后平均修复时间与降额后平均调整时间。

1.2 光伏发电可靠性评估模型

并网光伏系统由光伏电池模块、DC-DC变换器、DC-AC逆变器、控制器及滤波模块等组成。

光伏电池模块产生直流电，通过DC-AC逆变器进行直-交变换接入电网。光伏电池、DC-DC变换器、DC-AC逆变器及滤波器等元件的故障均会导致光伏系统并网的失败[8]。

考虑到元件故障与太阳照射的原因，将系统的工作状态进行简化，简化后的光伏系统状态转移示意图如图2所示。

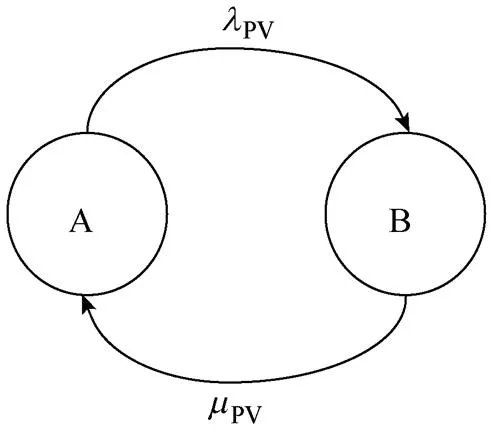
图2 光伏系统状态转移示意图

图2中，A为正常状态，B为停运状态，停运状态包括光伏机组因防孤岛保护切断与电网的连接或光伏机组故障（包括光伏电池阵列、DC-DC变换器、滤波器模块及DC-AC逆变器四种故障情况）。PV为光伏系统的故障发生率；PV为光伏系统的故障修复率。

在光伏发电系统双状态模型里，PV与PV对应光伏发电系统故障状态的发生率与修复率，单位为次/年。一般来说，光伏并网系统的具体组成与具体参数很难获取，修复时间等各项时间参数也难以精确计算，因此，故障率PV与修复率PV需要参考现场数据及专家工作经验等方面因素进行估算。

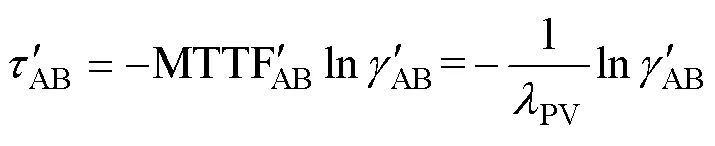
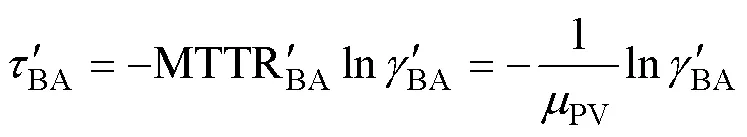
1.3 常规火力发电可靠性评估模型

常规火力发电系统状态转移模型，可以分为两状态到五状态不等[9]，通过分析历年火力发电机组的故障和停运时长，可以发现其存在一定的统计规律。通常情况下，常规火电机组可能的运行状态有额定运行、降额运行、例年检修、突发故障等状态，其概率按照统计学规律可以设为固定值。

在本文的可靠性模型中，考虑到原始信息不完善，为对电力系统进行最可靠的静态稳定性分析，常规火力发电系统采用两状态转移模型。

常规火电机组起停概率模型中，具有两种可能状态：一种是正常运行时输出额定功率；另一种则是在故障、检修等状态下的停运形式，不输出任何功率。可表示为

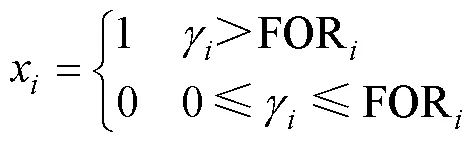
式中：x为发电机组起停状态；为[0, 1]内均匀分布随机数；FOR为强迫停运率。

常规火力发电系统也采用双状态转移模型，火电机组的正常运行持续时间与故障持续时间表示形式与式（5）和式（6）类同，不作进一步阐述。

2 基于序贯蒙特卡洛的可靠性评估方法

2.1 可靠性评估指标

电力系统中常用的可靠性指标有[9]：电力不足持续时间（loss of load duration, LOLD），电力不足概率（loss of load probability, LOLP），电量供应不足期望值（expected energy not supplied, EENS）。三种指标值越小，代表该系统越可靠。对电力系统可靠性进行评估时，既要考察失电概率，也要考虑失电后果，从而评价风险发生的可能性、严重性，因此，选用这三种指标作为系统可靠性评估指标，计及系统在不同运行状态下的数据波动性。三种指标表达式为

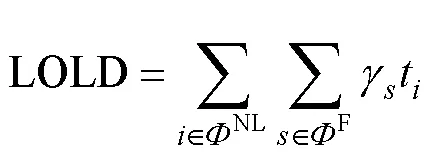
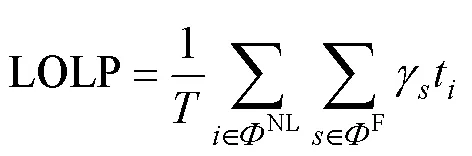
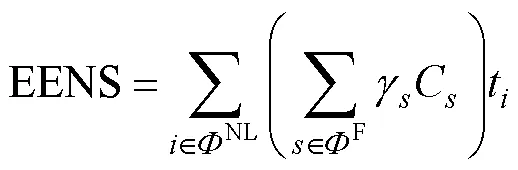
式中：t为第个负荷水平的时间长度（h）；为系统运行状态发生的概率；为系统运行状态的序数；C为状态的负荷供应不足量（MW）；为系统运行的总时间；F为多级负荷模型中第个负荷水平下系统出现负荷功率缺额的状态集合；NL为发电系统检修规划过程中负荷水平分级的集合。

2.2 序贯蒙特卡洛

序贯蒙特卡洛仿真能够考虑系统时序性等诸多因素，计算相关工作与时间因素作为可靠性评估指标，能够真实地模拟生产，计算各种经济指标，因此对系统可靠性评价起到了重要作用[10]。此外，风光互补发电系统模型需要体现时序特性，此时就需要把年度长时间尺度整个系统的运行状况都反映出来。

首先基于场景生成算法，生成风电、光伏出力的时序数据；接着与负荷模型结合，计及风光系统的约束条件，判断出系统当下的运行状况；然后进行大规模模拟，统计得到可靠性指标LOLD、LOLP与EENS。序贯蒙特卡洛模拟流程如图3所示。

图3 序贯蒙特卡洛模拟流程

3 计及发电系统可靠性的风光容量配比优化模型

3.1 经济性评估指标

经济性评估指标包括可再生能源规划建设成本、可再生能源年度补贴收益、常规火电机组年度运行成本、发电市场碳收益、系统电量损失总成本。

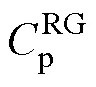
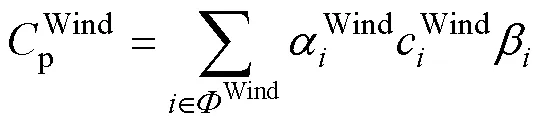
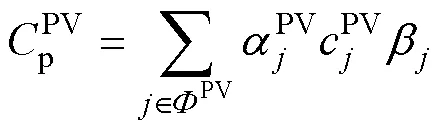
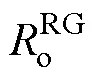
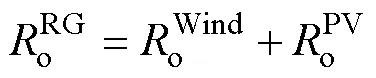
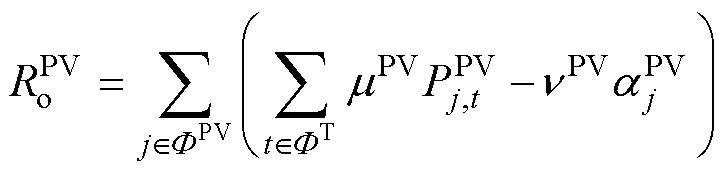
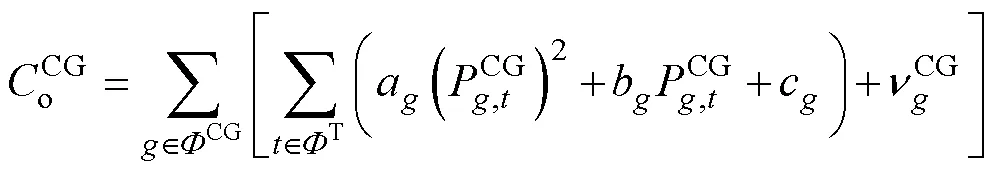
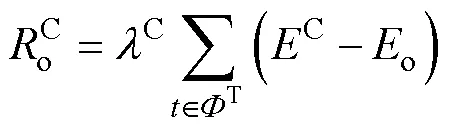
本文使用产电比及平均电价折算倍数的平均加权来构建系统的电量损失评估模型，以降低对缺电损失的估算误差。发电系统的可靠性成本函数表示为

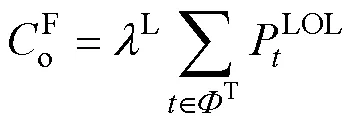
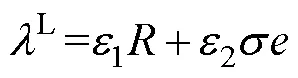
3.2 目标函数

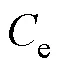
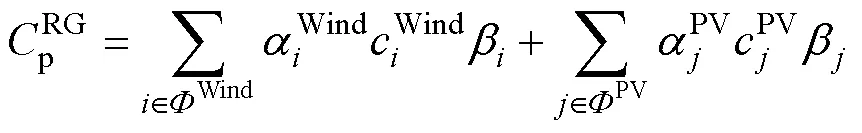
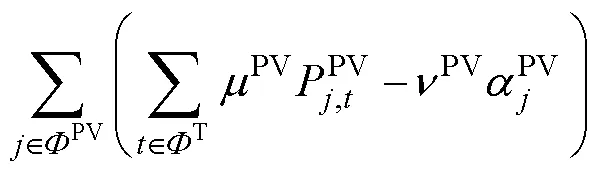
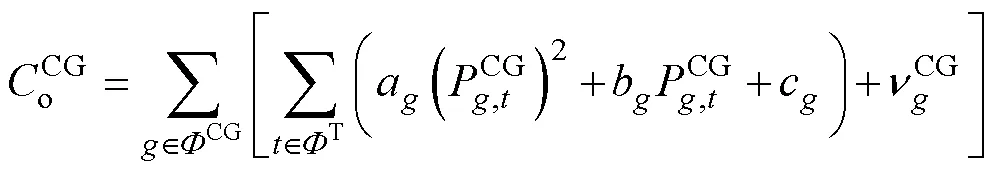
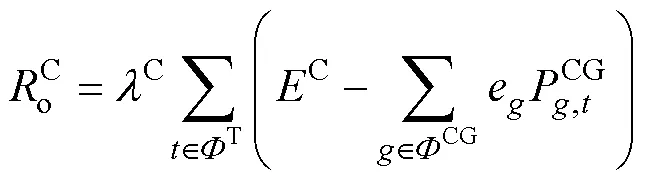
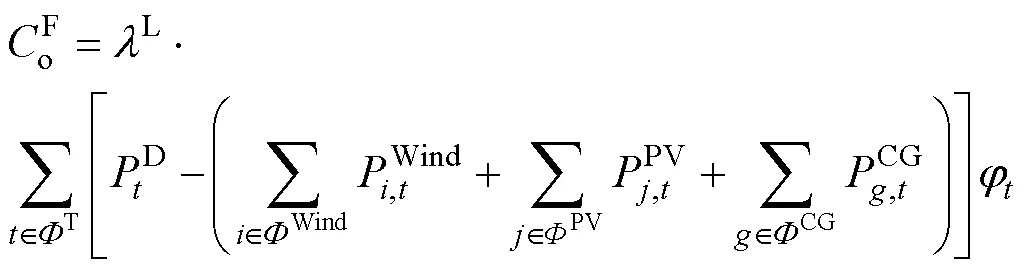
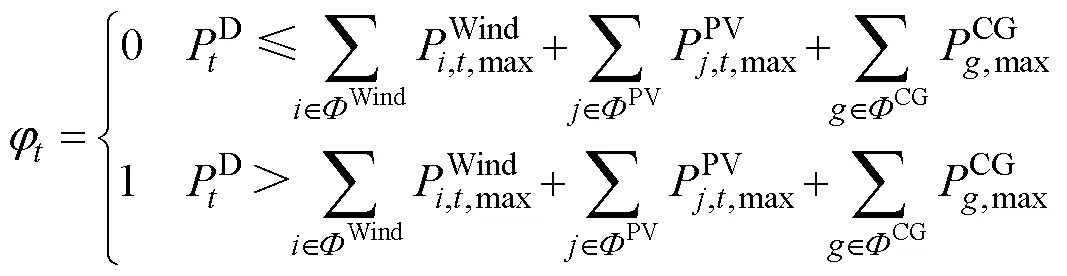
3.3 约束条件

本文构建包含常规火电机组与可再生能源机组的电源扩展规划模型，该模型涉及的约束条件表述如下。

（1）功率平衡

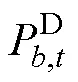
（2）火电机组功率限制

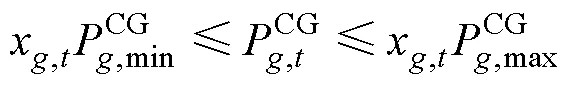
（3）可再生能源发电机的功率限制

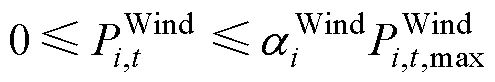
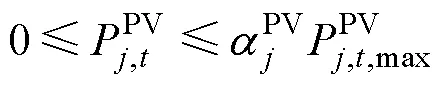
式（32）和式（33）分别表示风电机组、光伏

（4）可靠性约束

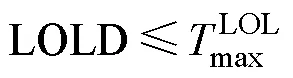
（5）线路的潮流方程和功率限制

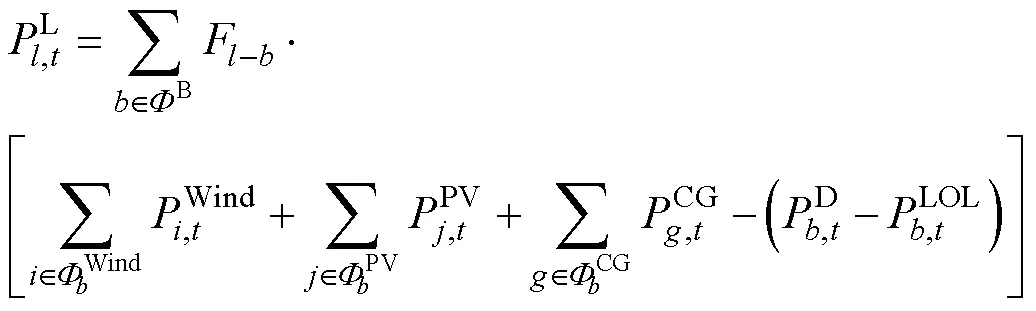
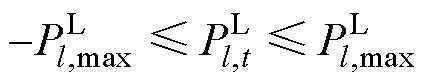
4 算例分析

4.1 IEEE-RBTS系统

将风光发电系统接入IEEE-RBTS系统进行仿真，火电机组具体参数详见文献[14]。以某地区的风速、光照强度及负荷数据为原始数据，结合该地区能源的时空分布特性和负荷的需求特性，分析典型算例下的风、光容量最优配比设计。

待建风电机组（单机额定功率2MW）成本为1 690万元/台，其使用寿命为20年，贴现率为6%；待建光伏机组成本为780万元/MW，其使用寿命为25年，贴现率为6%。风、光机组发电的补贴电价均为0.1元/(kW·h)。发电系统的碳价格为80.32元/t，火电机组的碳排放率为1.04kg/(kW·h)，发电系统的每小时允许的碳排放信用额为99.5t。电量损失赔偿机制中，产电比法与平均电价折算倍数法的加权平均系数分别为0.36、0.64，产电比为6.652元/(kW·h)，电价倍数为25，电力系统平均电价来自于江苏省现行实时电价。

为保证目标函数的收敛性与抽样模拟运算结果的稳定性，本文所构建的模型利用序贯蒙特卡洛方法，每一个规划方案模拟50次取均值。

为了分析风光互补特性对发电系统可靠性的影响，在发电机组规划建设中，采取如下四种电源规划策略（考虑到系统的常规火电机组容量充裕和响应减少碳排放政策的需求，不将火电机组的建设纳入规划中）以满足负荷增长需求。

策略1：电源扩展规划中，仅规划建设风电机组。

策略2：电源扩展规划中，仅规划建设光伏机组。

策略3：电源扩展规划中，同时规划建设风电机组和光伏机组，比例为2:1。

策略4：电源扩展规划中，同时规划建设风电机组和光伏机组，比例为1:2。

在对发电系统进行序贯蒙特卡洛规划模拟与风电容量配比优化过程中，风电容量、光伏容量各自按10MW等步增加容量建设，得到系统的电力不足持续时间、发电系统的年度运行总成本和风光建设成本等年值随建设容量的变化关系如图4与图5所示。其中，年度运行成本包括可再生能源年度补贴收益（取负）、常规火电机组年度运行成本、发电系统碳市场收益和系统电量损失总成本。

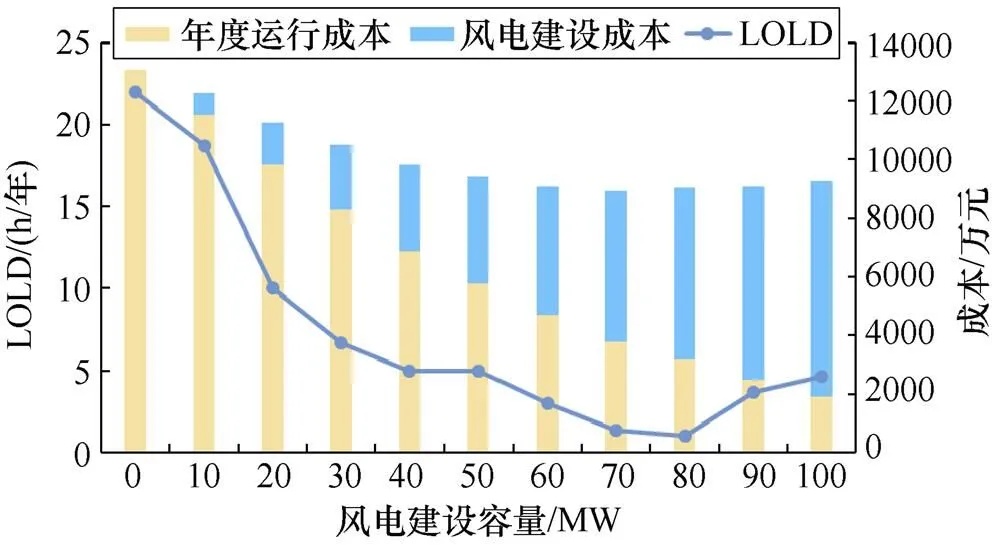
图4 风电机组建设容量对可靠性与经济性的影响

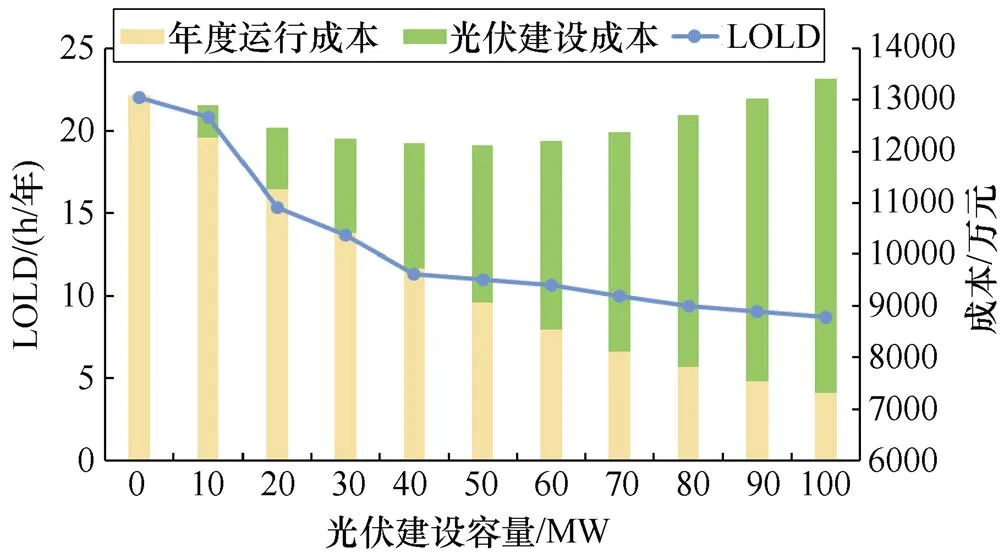
图5 光伏机组建设容量对可靠性与经济性的影响

从图4和图5可以看出，随着系统内可再生能源机组的扩建，对于系统可靠性而言，系统失电的风险呈现降低的趋势；对于系统经济性而言，可再生能源机组装机容量的增加必然导致其建设成本等年值的增加，而系统的总成本会呈现先降低后增加的变化规律——风电机组在70MW附近策略1总成本最低，光伏机组在50MW附近策略2总成本最低。原因在于，可再生能源在一定渗透率范围内，能够降低系统的电量损失成本和减小火电机组的燃煤消耗，进而实现对系统总成本的有效控制；然而，过度投建会导致系统内部可再生能源的过剩而消纳过低，系统可靠性增强不明显甚至会有所降低，装机建设的成本在总成本中逐渐突出。

对比策略1与策略2可以发现，在可再生能源机组扩展规划过程中，在同等装机容量下，策略1的电力不足持续时间小于策略2的值，策略1的年度运行成本远低于策略2的值，进而保证了策略1的总成本低于策略2。由此可知，风电机组对发电系统可靠性与经济性的影响均高于光伏机组，故在电源扩展规划过程中应当适当增加风电机组的占比。

基于本文建立的计及发电系统可靠性的风光容量配比优化模型，调用CPLEX，得到系统在规划70MW风电机组、33MW光伏机组时，能够在保证系统具备足够可靠性的同时，达到系统经济性最优的目的。此外，针对策略1与策略2，通过所构建模型的优化模拟，确定建设70MW风电机组时，策略1实现最优；建设47MW光伏机组时，策略2实现最优。

为了从不同的风光比例、不同装机容量的角度对发电系统的可靠性和综合成本（或效益）深入分析，对上述三种电源优化方案与初始方案（风光均不建设）展开详细对比，各指标数据见表1。

方案1：风光均不建设的基准方案（风0MW，光0MW）。

方案2：仅建设风电的优化方案（风70MW，光0MW）。

方案3：仅建设光伏的优化方案（风0MW，光47MW）。

方案4：风光互补建设的优化方案（风70MW，光33MW）。

根据表1可知，方案1～4的总费用期望等年值分别为13 084.93万元、8 943.95万元、12 078.96万元和8 561.90万元。方案4的经济性显著，相比初始无风光建设的纯火电发电系统，该方案充分利用了风光的互补特性，实现风光差异系数最低，进而能够降低34.57%的总费用期望等年值。

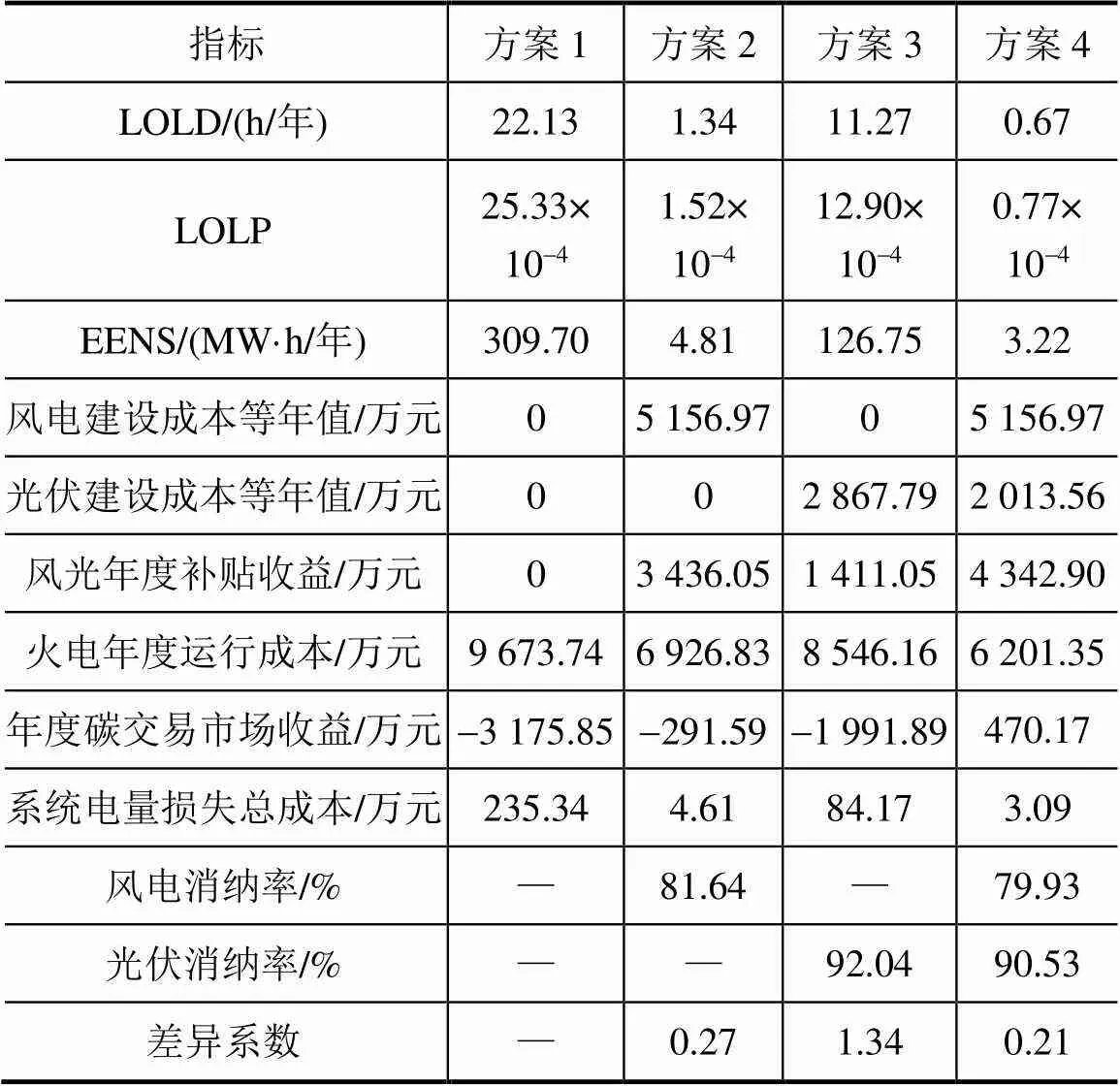
表1 四种电源规划方案下系统各指标数据

由于方案1中无风电或光伏机组，发电系统的机组出力仅为火电机组的出力，其年度变化情况如图6所示。

图6 方案1中发电系统的机组出力年度变化情况

因此，风电机组对发电系统可靠性与经济性的影响均高于光伏机组，在对发电系统进行规划时，更倾向于建设风电机组。比较方案2、方案3与方案4，系统在寻求最优风光容量配比的过程中并没有一味地增加风电的建设容量，而是辅以光伏机组的建设。结合预测的时序风速数据，某风电场7月典型日风速曲线如图7所示。

图7 某地区风电场7月典型日风速曲线

该时间段内，风电场出力具有较为显著的反调峰特性，即负荷高峰时，风机出力较少；负荷低谷时，风机出力较高，这导致风电机组的有效利用率降低。这一状况造成风电机组对系统负荷需求的支撑能力降低，而一定容量的光伏机组能够弥补风电的日出力反调峰的特点，共同实现负荷的削峰填谷。相比于仅建设70MW风电的方案2，该时间段内，方案4还建设了33MW的光伏机组，使差异系数减少至0.21，降低了22%。因此，方案4相比方案2与3，总费用期望等年值降低了4.27%与29.12%。

方案2～4的发电系统机组出力年度变化曲线分别如图8～图10所示。

根据图8～图10的年度机组出力仿真数据能够看出，对于6节点IEEE-RBTS系统，建设70MW风电机组和33MW光伏机组，能够充分实现风光资源的协调互补，有效降低火电机组的运行出力，从而获得更多的可再生能源年度补贴收益、发电系统碳市场收益，降低火电机组年度运行成本。

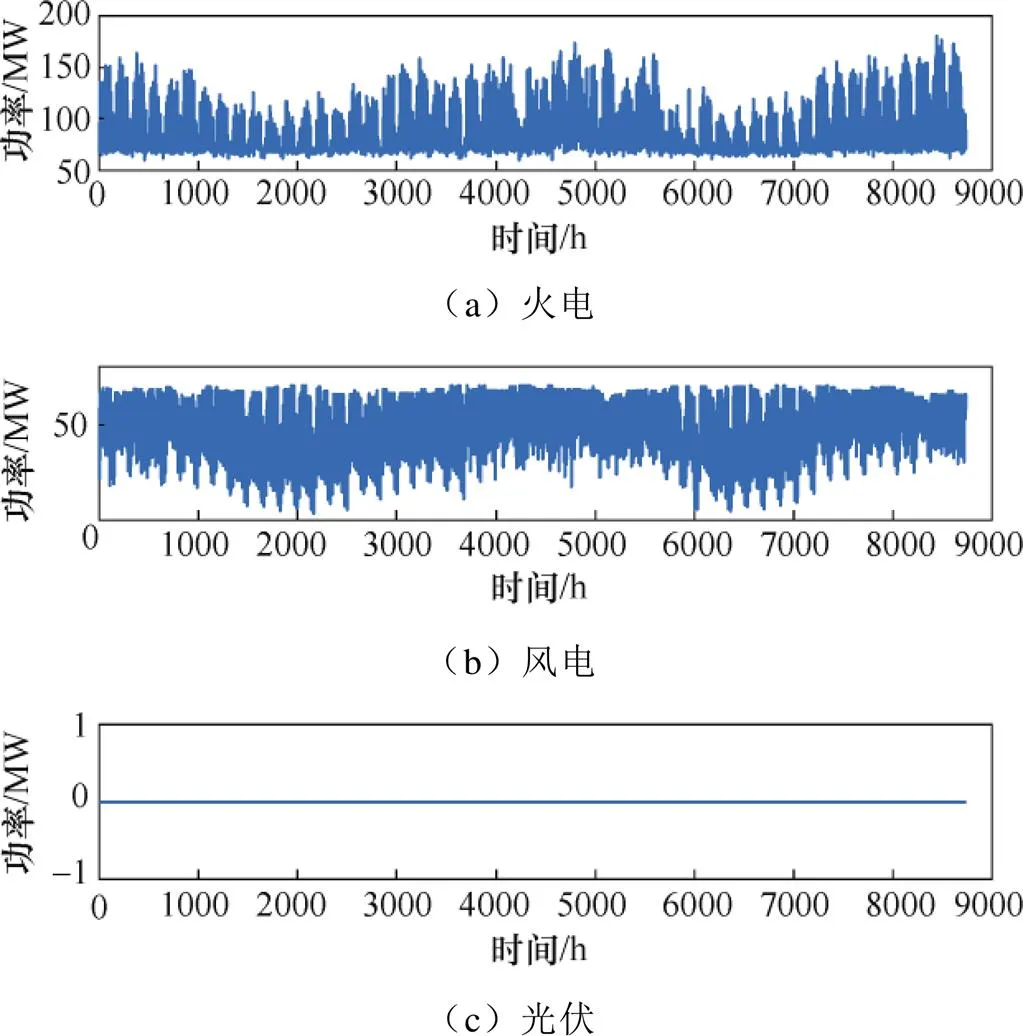
图8 方案2中发电系统的机组出力年度变化情况

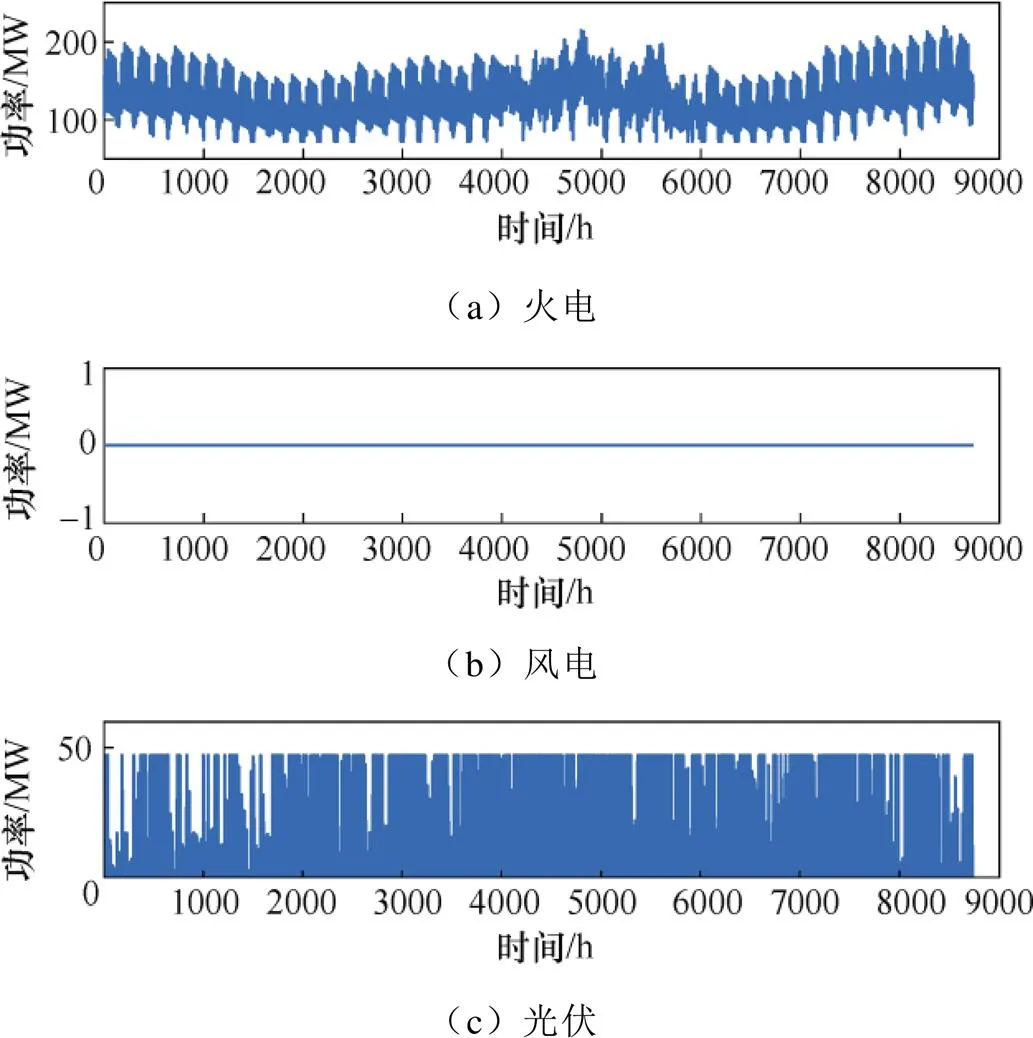
图9 方案3中发电系统的机组出力年度变化情况

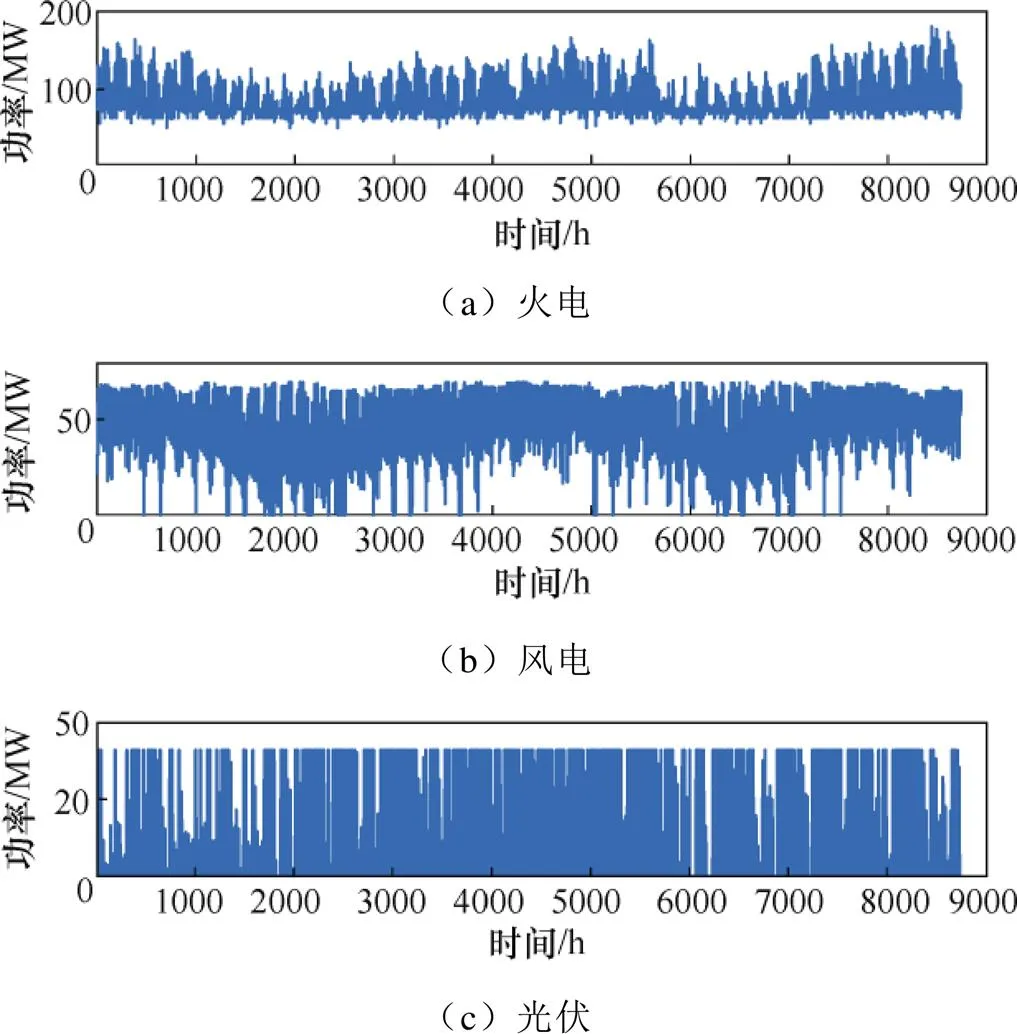
图10 方案4中发电系统的机组出力年度变化情况

观察风电机组和光伏机组出力可知，由于该地区风速大多分布在额定风速附近而光照在夜间为0，相比于光伏机组实际出力，风机实际出力更接近于额定功率，进而保证了系统获取更多的可靠性支撑。

此外，较之另外三种方案，方案4具有最高的可靠性，LOLD、LOLP和EENS分别为0.67h/年、7.7×10-5和3.22MW·h/年，将电量损失总成本降至了最低，为3.09万元，充分保证了发电系统可靠性。

综上所述，方案4为含风光出力发电系统的电源扩展规划最优方案，该方案充分发掘了风光互补的特性，确定了风电机组的最优配比——70MW风电机组和33MW光伏机组，即风电机组与光伏机组在总装机容量的占比为20.41%和9.62%时，所规划的电源扩展方案在保证系统足够可靠的同时，能够使发电系统经济效益最大化。

4.2 实际区域电网

4.1节对IEEE-RBTS系统进行了风光容量配比优化研究，设计的规划方案兼顾了发电系统的可靠性与经济性。为了进一步验证模型对实际电网的有效性与可行性，本节以某地区区域电网为例进行算例分析，该区域电网拓扑如图11所示。

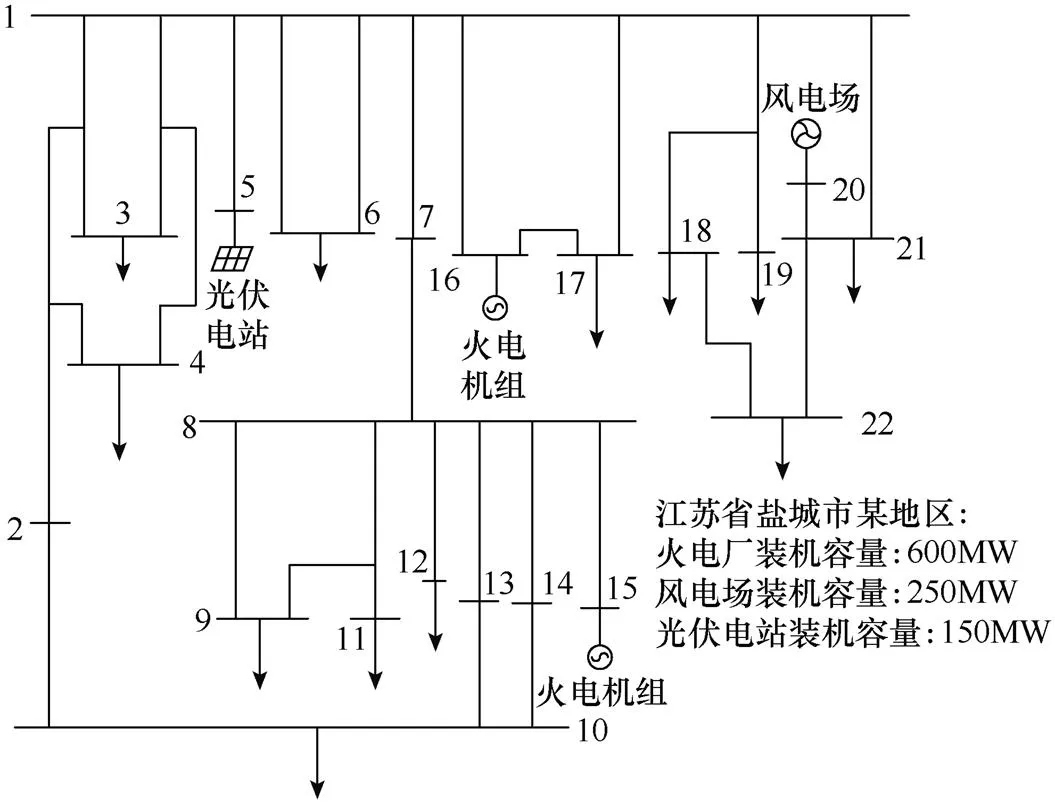
图11 某区域电网拓扑

在该区域电网中，常规机组为2台总装机容量600MW的火电机组；可再生能源已有装机总容量400MW，包括装机总量250MW的风电场及装机总量150MW的光伏电站。考虑到网络内新用户的接入及网络内用户电量需求的提高，负荷增长率为5%，该区域电网亟需提高发电系统的总装机容量。为更好响应节能减排的能源发展战略，计划建设风电和光伏机组，待建机组经济成本与可靠性数据同4.1节所述。该区域电网内，风电场最大规划装机容量为500MW，光伏电站最大装机容量为300MW。

与4.1节类似，基于本文构建的优化模型，得到四种规划方案。

方案1：风光均不建设的基准方案（风250MW，光150MW）。

方案2：仅建设风电的优化方案（风417MW，光150MW）。

方案3：仅建设光伏的优化方案（风250MW，光286MW）。

方案4：风光互补建设的优化方案（风417MW，光201MW）。

四种方案优化的数据见表2。

结合表2数据可以看出：在仅建设风电的情况下，该区域电网新建167MW的风电机组能够实现最优，总费用期望等年值为6.89亿元；在仅建设光伏的情况下，该区域电网新建136MW的光伏机组能够实现最优，总费用期望等年值为9.42亿元；在风电、光伏互补建设的情况下，该区域电网新建167MW的风电机组与51MW的光伏机组能够实现最优，总费用期望等年值为6.45亿元。方案4不仅利用了风光互补的特性，降低了差异系数，增加了可再生能源的上网容量，还降低了区域电网的电力不足持续时间，提高了整体的可靠性。

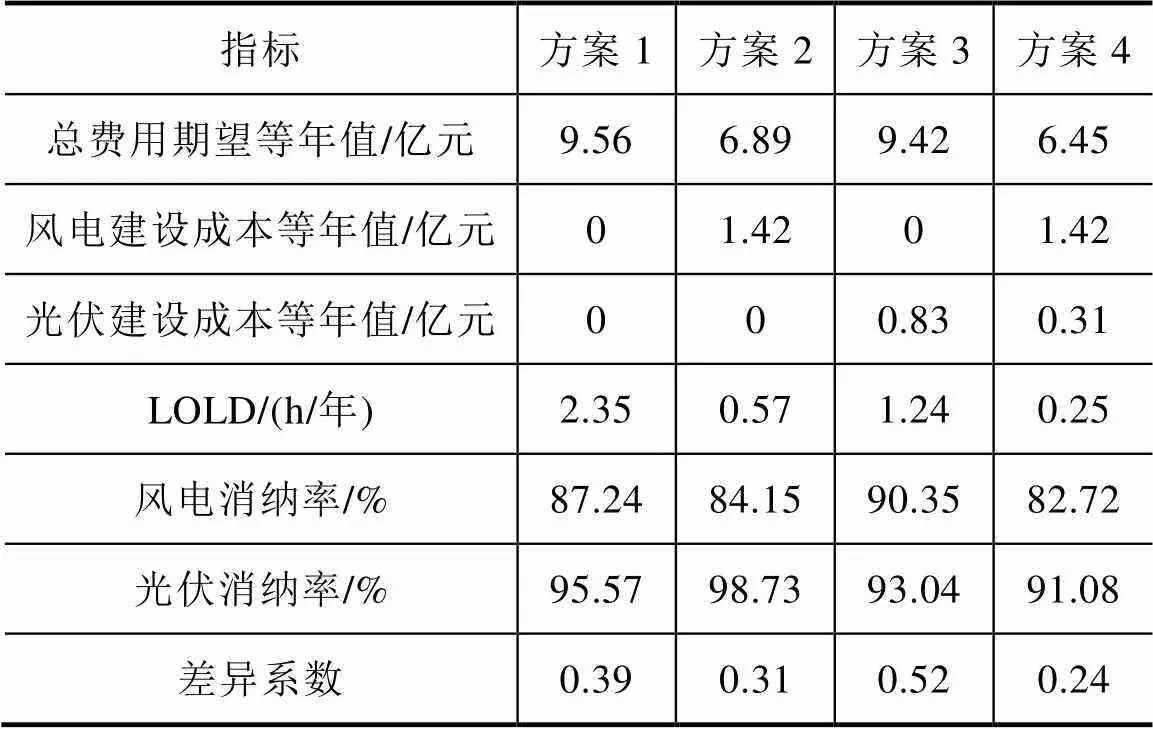
表2 四种电源规划方案的数据分析

图12展示了上述四种规划方案对区域电网可靠性与经济性的影响。方案4同时规划了区域电网内的风电与光伏装机容量，合理配置了新建风电场与光伏电站的容量，实现了目标函数总费用的最小化。该方案的建设成本等年值为1.73亿元，以投资新建167MW的风电机组与51MW的光伏机组为代价，相比于基准方案（方案1），实现了总费用期望等年值32.53%的降额，并降低了89.36%的电力不足持续时间，兼顾了区域电网的经济性与可靠性。

图12 不同规划方案对区域电网可靠性与经济性的影响

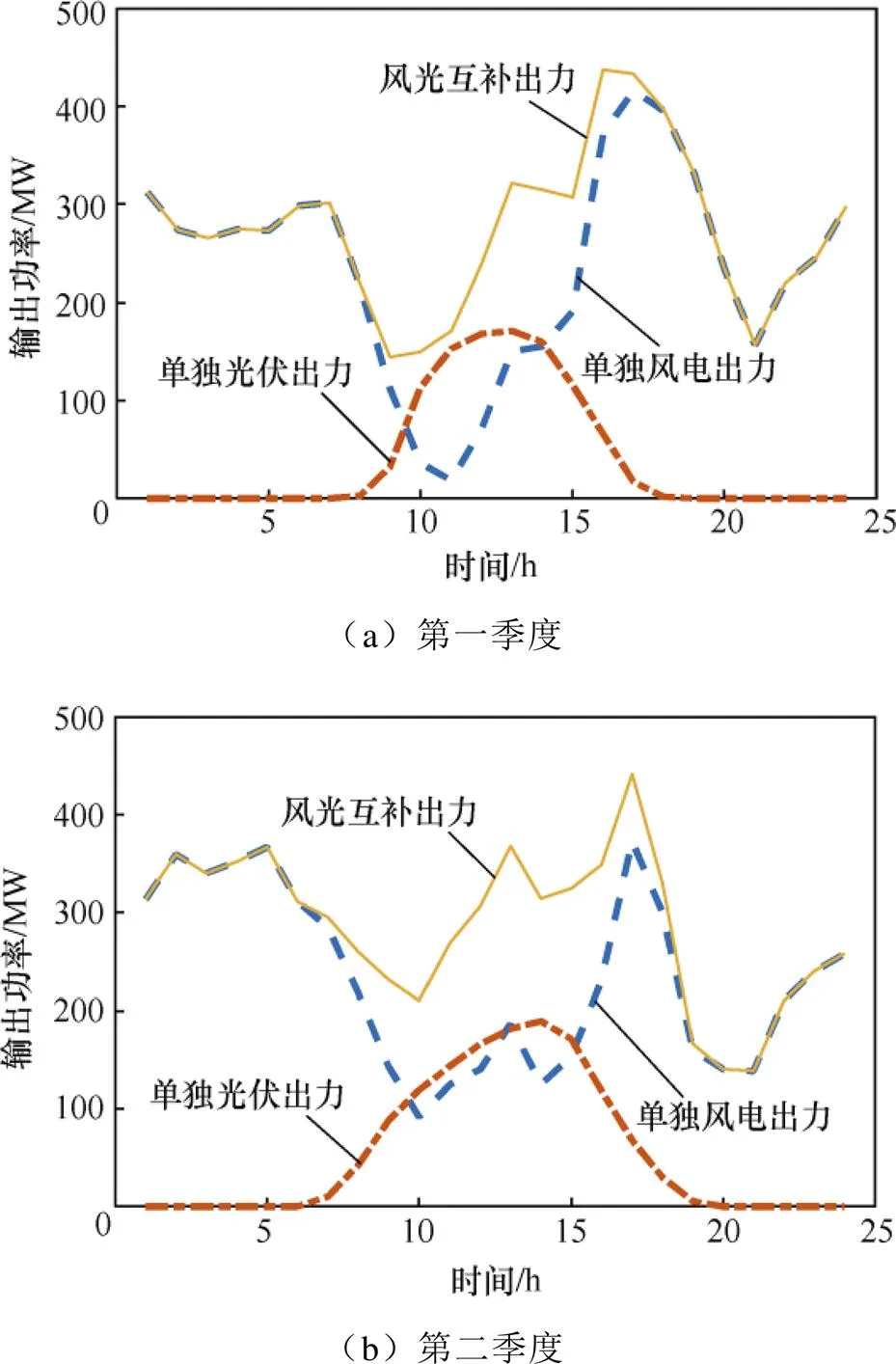
作为该区域电网的最优电源规划方案，方案4的可靠性已在4.1节进行了详细的讨论。同时，风光的互补特性是影响电源规划经济性的重要因素。因此，以方案4作为运行场景，讨论在规划机组投运后，不同季度下该区域电网风光互补发电的日平均输出功率情况，如图13所示。

图13描绘了方案4在四个不同季度下的风光互补发电日平均输出功率。由于该区域风电场具有明显的反调峰特性，相比于单独风电出力与单独光伏出力，风光互补出力的总输出功率更加稳定，尤其是在08:00～18:00期间，风光的输出功率曲线得到了有效的改善。

根据方案4的优化结果，可得到在规划建设后含417MW风电机组与201MW光伏机组的发电系统中，不同发电模式下的风光差异系数对比见表3。

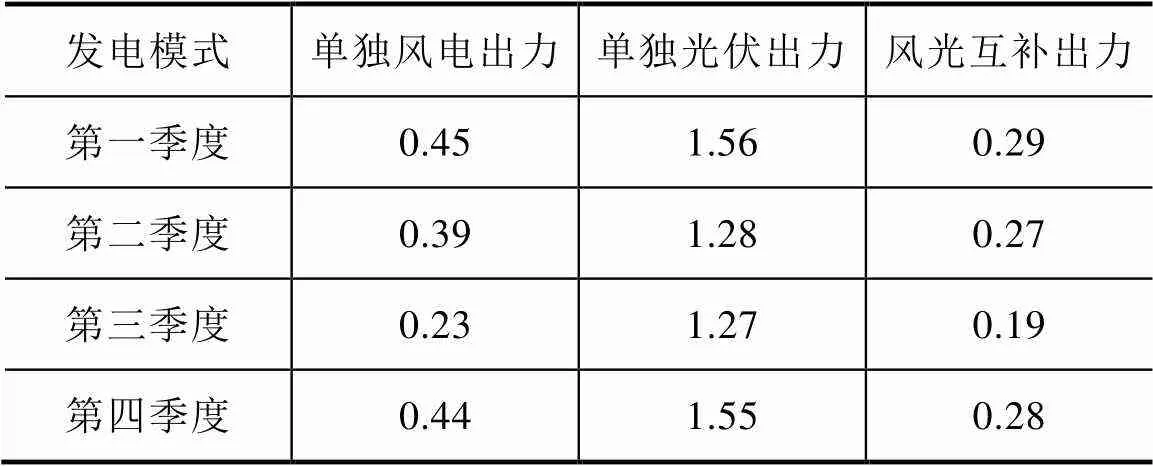
表3 最优规划方案下不同发电模式的差异系数对比

结合四个季度可再生能源不同发电模式的对比，可知风光互补出力的差异系数均小于单独风电出力与单独光伏出力的差异系数，表明风光互补发电的总输出功率更加稳定。

5 结论

本文首先建立了风力发电机组三状态停运模型、光伏发电机组和常规火电机组双状态停运模型；通过序贯蒙特卡洛统计得到可靠性指标；然后综合考虑可再生能源规划建设成本、可再生能源年度补贴收益、常规火电机组年度运行成本、发电系统碳市场收益及系统电量损失总成本五个因素，构建了计及发电系统可靠性的风光机组容量配比优化模型。在IEEE-RBTS系统及实际区域电网进行仿真分析，结果表明：

1）在电源扩展规划过程中，风光装机总容量的提高一定程度上能够降低系统的EENS、LOLD与LOLP，增强系统的可靠性；同等容量的情况下，风电机组相比光伏机组能够使系统获得更高的可靠性。

2）当风光渗透率达到临界点时，加大风光装机建设对系统可靠性的影响不再明显，甚至会产生负面作用。

3）合理配置风、光的机组容量能够让风光出力曲线变得更加平缓，减少单一类型可再生能源出力的波动性。

[1] 周亚敏. 以碳达峰与碳中和目标促我国产业链转型升级[J]. 中国发展观察, 2021(增刊1): 56-58.

[2] 李芸. 含大规模可再生能源的电力系统可靠性评估[D]. 银川: 宁夏大学, 2020.

[3] 郭光华, 杜颖, 范云鹏, 等. 以电为核心的综合能源系统研究综述[J]. 山东电力技术, 2021, 48(8): 1-7, 24.

[4] 陈聪伟, 江修波, 刘丽军. 考虑时序与储能配合的分布式电源优化配置研究[J]. 电气技术, 2017, 18(6): 41-47.

[5] 徐伟, 陈俊杰, 刘毅, 等. 无刷双馈独立发电系统的改进无参数预测电流控制[J]. 电工技术学报, 2021, 36(19): 4002-4015.

[6] 汤伟, 杨雪瑞, 姚恺丰, 等. 基于风电规模化入网技术的机组启停间歇联合协调方法研究[J]. 自动化技术与应用, 2021, 40(11): 144-148.

[7] 朱晨曦, 张焰, 严正, 等. 采用改进马尔科夫链蒙特卡洛法的风电功率序列建模[J]. 电工技术学报, 2020, 35(3): 577-589.

[8] 应飞祥, 汪宇航, 李琰, 等. 计及可靠性的含风光机组小型发电系统经济性评估[J]. 电气工程学报, 2020, 15(3): 13-21.

[9] 金尧, 王瑜, 胡庆虎. 考虑间歇性能源的发输电系统风险评估[J]. 电气技术, 2017, 18(5): 68-70, 73.

[10] 白桦, 王正用, 李晨, 等. 面向电网侧、新能源侧及用户侧的储能容量配置方法研究[J]. 电气技术, 2021, 22(1): 8-13.

[11] 唐念, 夏明超, 肖伟栋, 等. 考虑多种分布式电源及其随机特性的配电网多目标扩展规划[J]. 电力系统自动化, 2015, 39(8): 45-52.

[12] 应飞祥. 计及可靠性的含风光互补发电系统经济性评估及新能源消纳研究[D]. 昆明: 云南民族大学, 2019.

[13] 陆明璇, 周明, 黄瀚燕, 等. 含快速线路筛选的电力系统发输电协同优化运行[J]. 中国电机工程学报, 2021, 41(20): 6949-6959.

[14] BILLINTON R, KUMAR S, CHOWDHURY N, et al. A reliability test system for educational purposes-basic data[J]. IEEE Transactions on Power Systems, 1989, 4(3): 1238-1244.

Optimal proportion study of wind-solar hybrid generation system considering reliability

SONG Yu LI Han CHU Haoxiang LI Bin

(State Grid Jiangsu Electric Power Co., Ltd Extra-High Voltage Branch Company, Nanjing 211102)

Wind power and photovoltaic power generation systems have the characteristics of natural volatility and randomness, which increases the difficulty of risk assessment of power generation systems. In this paper, the sequential Monte Carlo method is used to study the reliability of power generation system, the optimization goal is to minimize the expected annual value of the total cost of the planning and operation of the power generation system, considering factors such as the planning and construction cost of renewable energy, the annual subsidy income of renewable energy, the annual operating cost of conventional thermal power units, the carbon market income of the power generation system, and the total cost of system power loss, etc. An optimization model for the capacity ratio of wind and solar power units considering the reliability of the power generation system is established. Finally, the optimal ratio of wind and solar power generation capacity under a typical example IEEE-RBTS system is studied, and further simulation verification is carried out in a certain regional power grid. The calculation example analysis verifies the validity of the model.

Monte Carlo; wind-solar hybrid; reliability; economy

2021-12-15

2022-01-18

宋 宇（1989—），男，江苏省南通市人，硕士，工程师，主要从事继电保护及自动化相关工作。