拟间歇振动辅助偏摆车削的切削力研究
卢明明,庄绪龙,陈斌,周家康,林洁琼
(长春工业大学 机电工程学院,长春 130012)
随着制造业的发展,钛合金[1-2]、镍基高温合金[3-4]和复合材料[5]等一些具有优良性能的难加工材料在航天航空、汽车、生物等领域被广泛应用。由于难加工材料的切削性能较差,采用传统加工方式容易产生裂纹、残余应力等缺陷。
近年来,国内外许多学者对切削力金属切削过程中产生的切削力进行了深入的研究。河南理工大学的焦锋教授通过有限元仿真建立一种超硬合金的切削力模型,分析了椭圆振动切削超硬合金时切削力随时间变化的关系[6]。中国民航大学的王涛教授采用ABABUS软件建立了碳纤维增韧树脂基复合材料高速铣削的渐进损伤切削力模型,并由切削实验分析了纤维方向对铣削过程中切削力、应力以及材料失效的影响机制[7]。哈尔滨工业大学的张晨峰使用有限元分析了加工V形槽时切削力的变化[8]。
在1994年由日本学者Shamoto和Moriwaki[9]针对一维振动切削技术提出椭圆振动切削技术(Elliptical vibration cutting,EVC),Zhang等[10]根据EVC的切削特点,分析了瞬时切削厚度、瞬时剪切角、瞬时摩擦逆转等特性的变化规律,建立了正交EVC过程的分析力模型,并进行低频正交EVC实验验证了该模型的正确性。Kim等[11]采用EVC方法研究了不同倾角下刀具所受切削力的变化规律的实验。Ammouri等[12]在EVC过程中建立了关于切削力和进给力的模型,并通过实验验证模型的正确性。Weng等[13]提出了一种考虑刀尖圆弧半径影响的预测车削操作中切削力的分析模型。Razavi等[14]根据斜角超声振动辅助车削的切削机理,分析了速度、频率、振幅、刃倾角以及法向刀具前角等参数对切削力的影响,建立了超声振动辅助斜角车削的动力学分析的理论模型。虽然对于切削力的研究已经十分成熟,许多切削力模型已被建立,并得到实验验证。但对于切削力分析需要大量运算。因此,建立一个能有效预测切削力变化,并且有较少运算量的切削力模型具有重要意义。拟间歇振动辅助偏摆切削(Qusi vibration assisted swing cutting,VASC)是针对难加工材料高效切削提出的一种拟间歇切削方法,其特有的拟间歇切削对于提高难加工材料加工效率、切削复杂结构精密零件都具有较大优势。切削力对工件材料已加工表面有重要影响,分析有助于揭示VASC温度、应力变化和表面完整性。目前,研究VASC的方向集中于路径规划、系统控制和装置设计等[15]。然而,现阶段对于VASC过程中切削力研究尚未成熟,需要进行深入研究。
综上所述,本文提出一种基于VASC的切削力模型,并利用VASC装置进行切削实验,通过Kistler三向测力仪采集VASC过程中的力数据,与切削力模型预测得结果进行比较,验证该模型的有效性。
1 VASC装置
为实现难加工材料高效加工,改善零件加工质量、提高加工效率,本课题组自主设计了一种VASC装置[16]。图1所示为VASC装置示意图,该装置由柔性装置、上盖板、压电驱动器、电容式位移传感器夹座、三向力传感器、电容式位移传感器、电容式位移传感器测量挡板和金刚石刀具组成。

图1 振动辅助偏摆切削装置
2 VASC切削力的分析与建模
2.1 VASC切削过程
图2所示为VASC切削过程,刀具以角度i摆动。取刀尖圆弧的中心点P,X轴过P点;Y(Y′)轴过P点且与刀具的前刀面垂直;Z轴过P点且与XY平面垂直。同时,X′与工件进给方向对齐;X′Y′平面与刀具前刀面垂直。
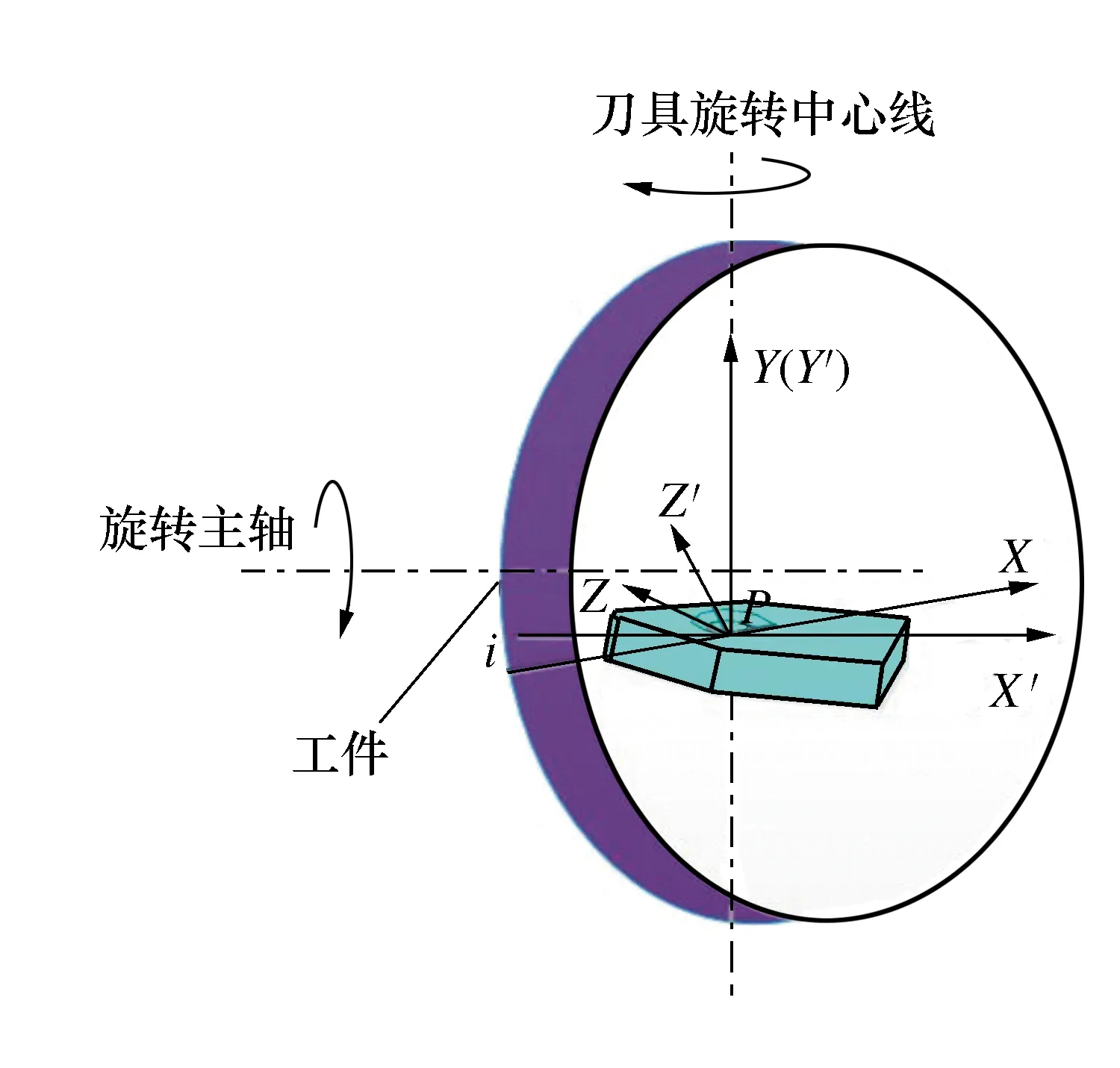
图2 振动辅助偏摆切削端面示意图
在摆动切削过程中,定义了剪切面、前刀面、已加工表面和法平面XZ。其中,刀具切削轨迹与法平面XZ平行。如图2所示,刀具摆动由压电驱动器以频率f来回驱动。此外,工件沿X′轴以速度Vf进给运动,相对于工件刀具的运动轨迹可用笛卡儿坐标表示为
(1)
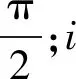
将刀具运动轨迹分别对时间t求导可得到其运动速度。则刀具相对于工件运动速度为:
(2)
2.2 瞬时剪切角、速度关系和瞬时摩擦反转特性
将VASC切削过程分为初始切削阶段和摩擦力逆转阶段,在初始切削阶段每一瞬时时刻都类似于普通切削阶段。几何关系类似,只在速度方向有所变化。图3所示为摆动切削过程中,某一瞬间时时刻的几何关系图。其中φn为法向剪切角,φi为摆动的剪切角,θn为合力的法向角,θi为合力的摆动角,η为切屑流出角。

图3 振动辅助偏摆切削的瞬时几何关系图
基于薄剪切理论和最大剪应力理论,在切削过程中,各速度间的关系可表示为
Vs=Vt-Vct
(3)
式中:Vs为瞬时剪切速度;Vt为工件相对于刀具的瞬时切削速度;Vct为切屑相对于刀具的瞬时速度。
在VASC切削过程中,由于摆动切削速度几何关系主要集中在法平面内,在这里将摆动切削过程分为3个切削阶段,即初始切削阶段、摩擦力逆转阶段、摩擦力逆转后阶段。图4a)为是普通切削的速度关系图,其中V表示相对于工件的刀具速度,Vc为切屑速度,Vs为剪切速度。它们的速度大小和方向恒定,图4b)~图4d)显示了VASC在两个不同区域的速度。其中:两条虚线(OS和OS′)表示剪切速度Vs的两个恒定方向。图4b)为VASC切削过程初始切削阶段速度关系,初始切削阶段类似普通切削阶段,只在速度方向有一定变化,其中瞬时剪切速度方向与OS方向一样。并且假设剪切角φkc等于瞬时方向角θ。图4c)为VASC切削过程中的摩擦力逆转阶段,其中Vct为零,Vt和Vs方向一致,剪切角φkc随着瞬时方向角θ变化。图4d)为VASC切削过程中的摩擦力逆转后阶段,切削过程中切屑流动方向与刀具速度方向相同。并且剪切速度Vs方向与OS′方向一致,在这里剪切角φkr被视作另外一个常数。

图4 振动辅助偏摆切削过程的速度分析
基于上述分析,3个连续区域中瞬态剪切平面角φt可以用特定区域边界来描述,即:
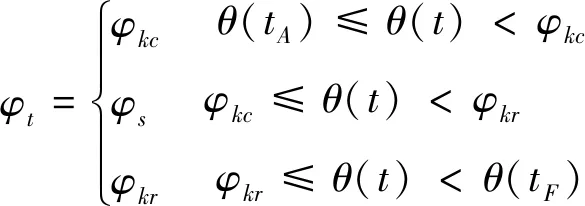
(4)
2.3 切削合力在法平面、前刀面及剪切面的分量
图5所示为VASC切削过程中合力R在法平面和前刀面投影。
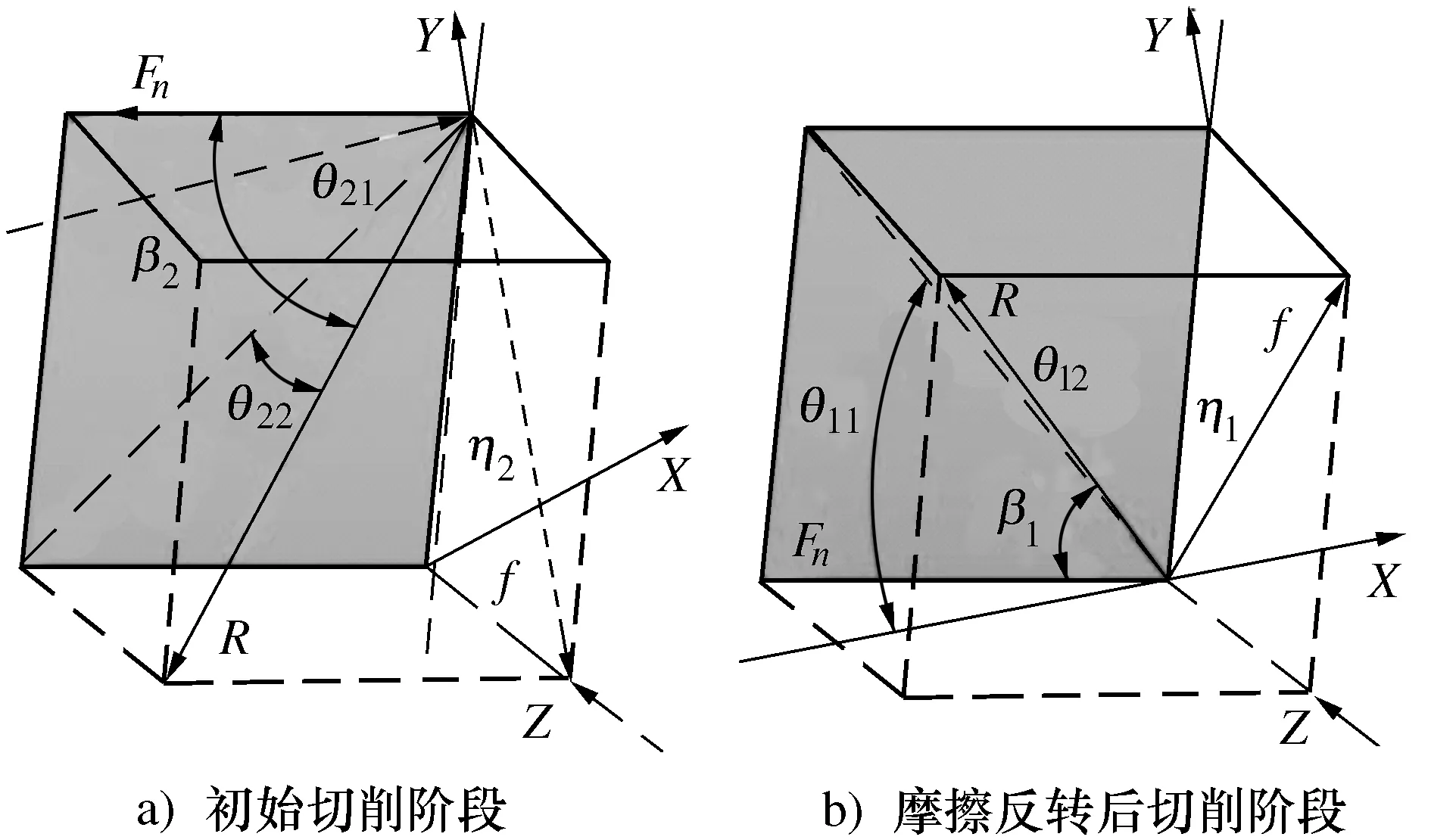
图5 合力R与法向力Fn、摩擦力f的几何关系
图5中:Fn表示垂直于刀具前刀面的力分量;f表示切屑与刀具前刀面之间的摩擦力;θn表示X轴与法平面XZ上的R投影之间的角度;θi表示R与法平面XZ之间的角度。β表示R与Fn之间的摩擦角。图5a)为摆动切削过程中初始阶段(类似普通切削阶段)的切削合力R与前刀面法向力Fn和摩擦力f的几何关系。图5b)为摆动切削过程中摩擦力反转后切削合力R与前刀面的法向力Fn和摩擦力f的几何关系。
由图5a)中可以得到VASC中初始切削阶段角度关系为:

(5)
由图5b)中可以得到VASC中摩擦力反转后切削阶段角度关系为:

(6)
由滑移线理论模型和切削力理论模型并结合材料力学,基于最大剪应力理论(Maximum shear stress theory,MSST),在VASC切削过程中初始切削阶段和摩擦力反转后切削阶段上的受力关系如图6所示。
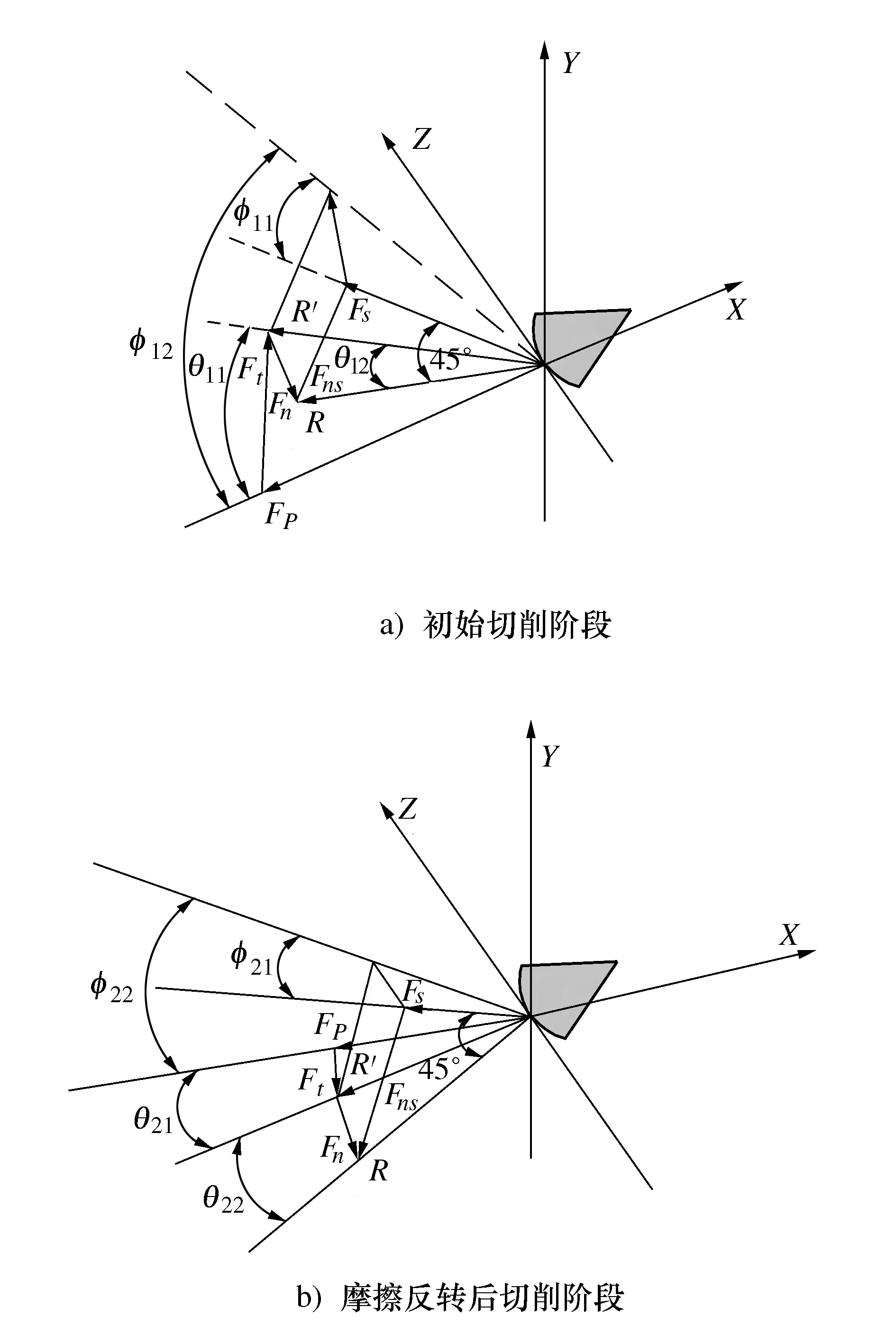
图6 初始切削阶段与摩擦反转后的切削阶段合力投影图
图6中:R表示3个方向上切削力的合力;R′表示合力R在法平面XZ上投影;Fp表示沿X轴方向轴向切削力;Ft表示沿Y轴轴向切削力;Fn表示沿Z轴轴向切削力;Fs表示剪切面上剪应力;Fns表示垂直于剪切平面剪切力。其中,Fp,Ft,Fn,为合力R在X、Y、Z这3个方向上分力,合力R与剪切力Fs的夹角为45°。3个方向上切削力与合力R和合力R′的投影在整个切削过程中关系如下:
(7)
在许多研究中普遍应用最大剪应力原理预测剪切角方向,由最大剪应力原理可知最大剪应力方向与合力方向的夹角为45°。因此,可以得到以下关系:
初始切削阶段
Fs=R[cosθi1cos(φn1+θn1)cosφi1+sinθi1sinφi1]
(8)
摩擦力逆转阶段
Fs=R[cosθi2cos(φn2-θn2)cosφi2+sinθi2sinφi2]
(9)
在切削过程中,基于最大剪应力原理预测了剪切角方向,同时根据材料力学的相关知识得到剪应力表达式可由下式表示

(10)
式中:As、m、h分别表示剪切面积、切削宽度和切削深度。在摆动切削过程中,由式(8)~式(10)可以求得初始切削阶段和摩擦力反转切削阶段的合力R的公式,表示如下:
初始切削阶段
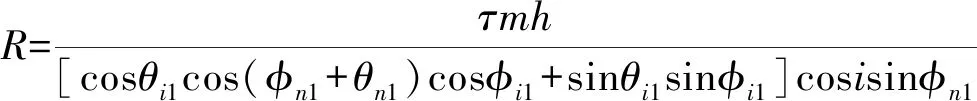
(11)
摩擦逆转阶段
(12)
3 VASC切削实验
3.1 VASC实验方案设计
利用Nanoform 250超精密单点金刚石车床,并结合VASC切削装置、可编程运动控制器(Programmable multi-axis controller,PMAC)、四通道电容式位移传感器5300、三通道压电功率放大器(PI E-500)、压电陶瓷驱动(40VS12)、测力仪系统(测力仪、电荷放大器、计算机)进行VASC切削直径为12.7 mm的铜棒材料的切削实验。
将铜棒近似安装在主轴中心上,将可编程运动控制器、三通道压电功率放大器、测力仪系统(测力仪、电荷放大器、计算机)等实验仪器进行连接。最后,将Kistle测力仪固定在Z向导轨上,同时将VASC装置固定在Kistle测力仪上。切削铜棒过程中,由数据采集卡采集数据。如图7所示为振动辅助偏摆切削实验系统图。

图7 振动辅助偏摆切削实验
3.2 不同转速下的切削力理论与实验对比
在切削过程中,切削力的大小对工件表面质量、表面粗糙度等因素影响尤为重要。为降低实验存在的误差,主轴速度设置为10 r/min、20 r/min、30 r/min、振动频率为10 Hz,振幅分别为10 μm,切深为0.03 mm,切削参数如表1所示。在把切削条件后设置完成后进行VASC切削实验。图8所示为不同切削速度下对应的切削力变化曲线,VASC的振动参数相同。在VASC切削过程中,实验分析测得的每一周期上的力峰值取和,并求出其平均最大切削力。

表1 不同转速下的切削参数
图8所示为实验测得主轴转速分别为10 r/min、20 r/min、30 r/min下的切削力值。图9所示为不同主轴转速下切削力的实验值与理论值变化趋势。

图8 不同主轴转速对应的切削力

图9 不同切削速度下切削力的实验与理论对比图
由图9可知,主轴转速由10 r/min增加到30 r/min的过程中,实验测得的切削力由12.6 N增加16.3 N,理论分析得到的切削力由11.7 N增加到15.7 N。这是由于装置安装、环境噪声等的误差导致实验测得力数据与理论计算力数据存在偏差。另外,当主轴转速由10 r/min增加到20 r/min的过程时,实验测得切削力值增加了1.3 N,理论分析的切削力值增加了1.1 N。主轴转速由20 r/min增加到30 r/min的过程中实验测得切削力值增加了2.4 N,理论分析切削力值增加了2.9 N。主轴转速由20 r/min增加到30 r/min时切削力的增值较大,这是由于随着切削速度的增加,刀具与工件的挤压增强。
3.3 不同切深下的切削力理论与实验对比
为降低实验误差且保证实验稳定进行,切削深度设为0.01 mm、0.02 mm、0.03 mm,切削速度为0.35 m/s,振幅分别为10 μm,频率为10 Hz,切削参数如表2所示。实验在超精密车床上展开,通过不同的进给设定实现了不同的切削深度。

表2 不同切深下的切削参数
图10所示为实验测得在切削深度分别为0.01 mm、0.02 mm、0.03 mm下的切削力值。

图10 不同切削深度对应的切削力
图11所示为不同切削深度下切削力的实验值与理论值变化趋势。

图11 不同切深下切削力的实验与理论对比图
在切削过程中当切削深度增大时,刀具挤压工件产生更大厚度切屑,VASC切削中切屑于前刀面作用力也相应增大。图11所示,切削深度从0.01 mm增加到0.02 mm时,实验测得的切削力由8.6 N增加到10.2 N,理论分析切削力值由7.8 N增加到9.2 N。切削深度从0.02 mm增加到0.03 mm时,实验测得切削力由10.2N增加到12.2N,理论分析切削力值由9.2 N增加到12 N。切削深度由0.02 mm增加到0.03 mm时,切削力增幅比切削深度由0.01 mm增加到0.02 mm时增加剧烈,这是由于随着切削深度的增加,刀具与工件挤压变大,致使刀具受力增大。
4 结论
本文建立了振动辅助偏摆切削的切削力模型,并通过理论分析与实验对比得到了以下的结论:
1) 由薄剪切面理论分析了振动辅助偏摆切削过程中瞬时剪切角和切削速度变化关系,建立了瞬态剪切平面角与时间t的表达式。最大剪应力理论和切削过程力的关系,分析了各相关角度与时间t的联系,建立了切削力分析模型。
2) 通过VASC加工铜棒实验,分析了不同主轴转速和不同切削深度下切削力变化情况,主轴转速从10 r/min增加到30 r /min时,实验和理论获得的切削力值分别增加了3.7 N和4 N,切削深度由0.01 mm增加到0.03 mm时,实验和理论获得的切削力值分别增加了3.6 N和4.2 N。结果表明,实验得到的结果与理论模型分析结果的变化趋势基本一致,验证了该模型有效性。

