水下移动发射平台设计与初步试验

康会峰，宣佳林，刘志宾，王 坤，曹睿智

（1. 北华航天工业学院 ，廊坊，065000；2. 河北省跨气水介质飞行器重点实验室，廊坊，065000；3. 河北省电动汽车充换电技术创新中心（筹），廊坊，065000）

0 引 言

潜射航行体的弹丸发射是一个涉及多因素干扰、多相介质参与的复杂物理过程。经过近几年的发展，各国已在水下发射平台的研制与使用方面积累了大量经验获得了相关数据，不仅理论与数值仿真研究方面取得一定的成果，还进行了大量的试验研究，特别是美国、俄罗斯等军事强国，相关试验研究较为深入。各国建设了围绕跨介质飞行器的试验研究的试验设备，中国对水下发射技术也开展了研究。方宁、宋召青等对潜载导弹在水下垂直发射过程进行了力学分析，对水下弹道模型进行了弹道仿真，研究了在不同水深条件、水流速度、发射初速下的运动姿态和相应的临界条件。孟祥宇、侯健等采用气体动力学理论，建立了弹炮配合间隙及气液两相相互作用的水下枪内弹道模型，对水下弹丸发射的内弹道进行了数值分析，总结了膛压和弹炮耦合间隙对射弹初速度的影响规律；张京辉、余刚等搭建了弹道枪水下可视化射击平台，对12.7 mm 弹道枪在水中全淹没方式的发射膛口的流场过程做了观测研究；杨继锋、刘丙杰等对潜射弹道导弹水下大深度发射技术进行了研究，给出了水下大深度发射技术的解决途径以及解决方案，研究主要偏重于弹体发射过程中的相关空泡、喷控技术等。曹嘉怡、鲁传敬等采用多相流mixture 模型，应用有限体积法（Finite Volume Method，FVM）和Simple 算法，求解气水两相混合介质的RANS 方程和standard-湍流模式，揭示了潜射导弹水下垂直发射过程中-湍流复杂多相流动的演化、流场结构和流体动力特性。综上所述，关于水下弹丸发射技术的相关研究主要集中在数值模拟和水下发射平台固定的方式，研究内容主要为水下发射的弹丸空化现象、流体动力特性和水弹道，关于水下多弹移动发射技术的试验仪器、试验设备的研究还较少，实验室内水下多弹移动发射的试验仪器设备的研究更未有相关报道。通过水下可移动发射试验研究可以获得相关发射过程中的水下航行规律、弹丸发射出水以及多弹发射过程中的多弹扰动规律等。同时实验室进行水下弹丸可移动发射试验可以降低试验成本，通过在实验室架设PIV 测量仪器设备获得试验数据，研究方便且可以重复试验，对水下多弹发射过程中的空化、多弹干扰技术以及水下弹道控制等方面的研究有重要的意义。

1 水下可移动弹丸发射试验系统设计

1.1 设计目标

建立一种水下移动发射平台，弹丸水下发射往往需要航行器在恒定速度时发射，由于实验室空间有限，为兼顾发射速度稳定与空间的关系，设定了如图1 所示的水下移动平台速度曲线，速度曲线分为3 段：启动段、恒速段和停止段。其中启动段设计最为困难，加速度大、启动距离短，可以有较长的试验距离或试验时间，但是运动过程速度较大，容易超过最高设定速度1.2 m/s。加速度小，速度控制难度小，但是启动距离长、恒速发射的距离或时间较短。因此，需选择合理的驱动方式，开展速度曲线的优化设计。

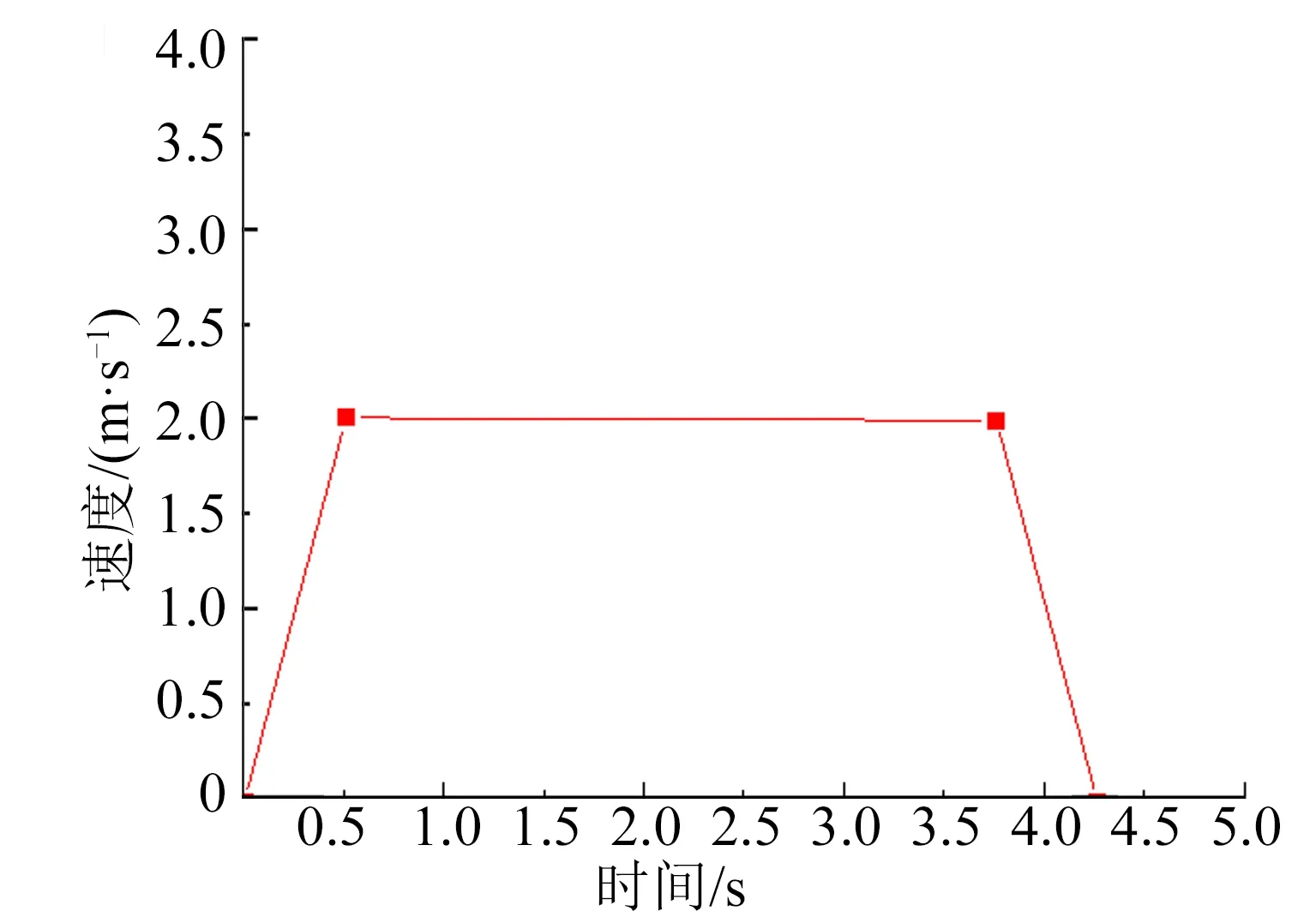
图1 移动速度与时间的关系Fig.1 The Relation between Moving Speed and Time

对于驱动方式，主要有以气炮工作原理为基础的模型驱动方式和以电机拖动为基础的模型驱动方式两种，综合考虑水平运动速度、经济性与可靠性等因素，选择电机拖动作为基础的模型驱动方式。以气炮工作原理为基础的模型驱动方式具有启动快的特点，但由于水的阻力和速度平方成正比，模型很难精确恒速。而本试验模型为缩尺模型，对速度精度要求较高，因此，最后确定采用电机拖动，采用电机拖动存在的主要问题就是启动过程慢，要缩短启动时间，需要提高电机的功率、扭矩等参数要求。电机驱动方式的核心是伺服电机的启动响应时间和调速精度，主要通过采用大功率伺服电机，加上减速器的方案，来解决这个问题。

伺服电机通过减速器减速，与卷扬机相连，通过钢丝绳拖拽水下可移动弹丸发射系统，需要在0.5 s 内能够将发射系统速度提升到2 m/s。钢丝绳的最大线速度为2m/s。按照卷扬机半径=200 mm（=400 mm）计算，减速器最大输出转速为10 转/min。

1.2 方案设计

水下移动发射平台主要包括如下部分：密闭水箱、发射平台、驱动系统和控制系统。其中密闭水箱用于模拟水下发射的液体环境和真空环境，由钢架焊接而成，正面使用有机玻璃替代了钢板以实现可视化；发射平台为实施发射的装置，内置有3 个高压空间，弹丸通过高压空气完成发射。驱动系统为发射装置的水平在轨移动提供动力，包含电机、减速器、卷扬机、钢丝绳、定滑轮等零部件，如图2 所示。电机经过减速器减速后，由卷扬机通过绳索驱动，借助定滑轮换向，对发射平台进行拖拽，实现发射平台水平在轨恒速移动。因此，发射平台的移动速度为试验系统设计的核心指标之一。控制系统包含发射系统控制和水平运动系统控制。试验前需根据试验时序图对控制系统进行调试，以在恒速下完成多次发射。

图2 试验系统示意Fig.2 Schematic Diagram of Experimental System

水下移动发射平台以北华航天工业学院与清华大学航天航空学院、河北省跨气水介质飞行器重点实验室联合研制的新型大口径轻气炮作为发射试验模型的载体，实现了水下移动弹丸跨水气介质发射，分析发射全过程的物理现象，该技术在相关的学术报道中已经进行了详细的阐述，在此不再做过多的论述。

1.3 发射平台受力分析

发射平台的受力包括水阻力、导轨摩擦力和驱动系统的牵引力。其中发射平台受到的水阻力和发射平台运动速度、发射平台在运动速度方向的投影面积相关，并且发射平台的水平移动属于变速度问题，难以通过简化理论分析准确给出阻力大小。通过仿真计算了阻力系数为常数时水平移动过程发射平台的受力情况。计算条件是：水平加速系统用0.5 s 加速到1.1 m/s，然后匀速运行2 s，完成模型弹发射之后，按照给定的减速运动规律，直至停止，如图1 所示，绘制网格为混合网格，网格数量为1 130 724，如图3 所示。

图3 试验系统表面计算网格Fig.3 Computational Grid on the Experimental System Surface

采用商业计算软件Fluent 计算了发射平台的受力情况，发射平台所受合力如图4 所示。

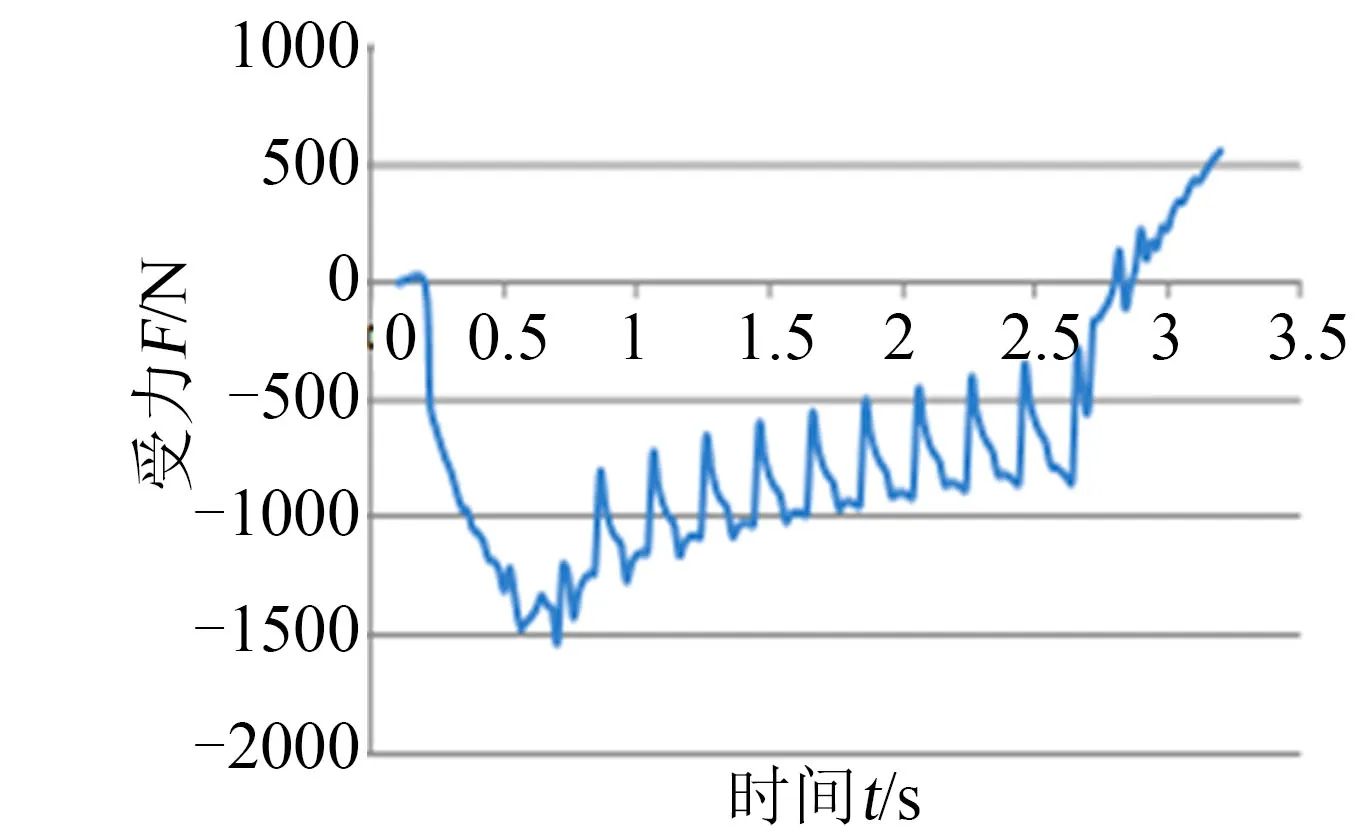
图4 水平移动过程发射平台受力曲线Fig.4 The Force-time Curve of a Horizontal Moving System

从图4 中可以看出发射平台所受的最大合力为1 500 N，在匀速移动过程中发射平台所受到的阻力出现震荡，原因是底座突然启动产生的冲击波在底座左端面和水箱左端面之间来回反射以及底座背水面诱导的卡门涡街。

考虑发射平台受电机拉力作用、摩擦力和水阻力，根据牛顿第二定律，有：

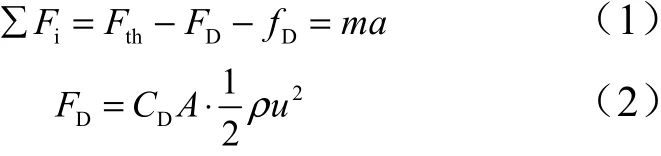
忽略摩擦阻力，即=0，只考虑发射平台所受电机拉力和水阻力，式（1）简化为

因此，可计算出电机拉力：

根据实际试验测得的水平速度与时间曲线，可大致计算出所需电机的约为200 N。各变量含义见表1。

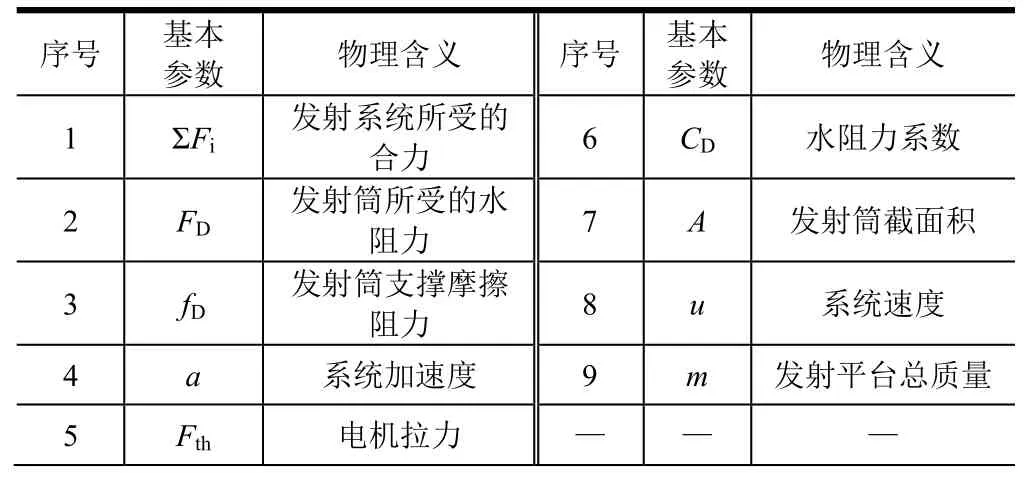
表1 各变量物理含义Tab.1 The Physical Meaning of Each Variable

1.4 驱动系统卷扬机设计与电机的选择

根据上述分析，驱动系统应选用机械响应迅速的电机，即中小惯量电机。因此需计算卷扬机的转动惯量，以此来评估电机响应速度，从而选择电机。根据水箱尺寸，拟选择带减速箱伺服电机带动卷扬机的驱动方式，卷扬机结构如图5 所示。

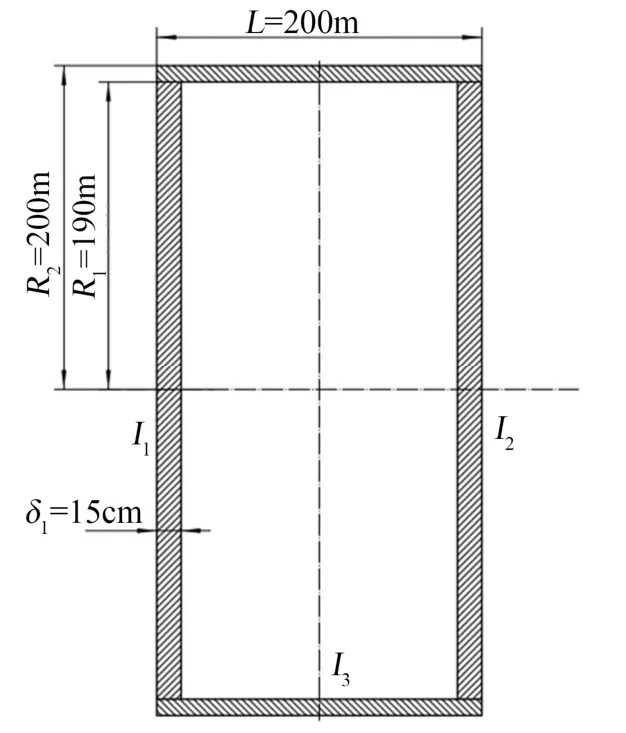
图5 卷扬机结构Fig.5 Winch Structure

卷扬机转动惯量计算如下：

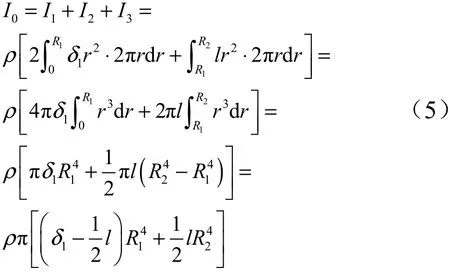
式中为卷扬机的转动惯量；为卷扬机左侧圆盘的转动惯量；为卷扬机右侧圆盘的转动惯量；为卷扬机卷筒的转动惯量。

卷扬机选用铝材进行加工，根据材料性质和实际尺寸，具体参数如表2 所示。

表2 卷扬机基本参数Tab.2 Basic Parameters of Winch

经计算卷扬机转动惯量为=0.41756 kg·m。确定匝数：根据式（6）可计算卷扬机的匝数。

式中为绕绳匝数，为卷扬机绕绳子的轮子直径，=400 mm；为模型的行程，=4 m，则线圈匝数为

预选安川电机，型号为SGM7G-75A，选择减速比为5:1 减速箱，由于电机通过减速机将扭矩传递给卷扬机，根据动能守恒定律，可知高转速轴转动惯量和低转速轴转动惯量有如下关系：

式中表示电机的转动惯量；表示减速机的减速比。因此，电机需要的最大转动惯量为=0.0167 kg·m。

电机参数如表3 所示，所选电机的转动惯量小于计算最大惯量，可应用于驱动系统。以下为重要参数进行校验过程。

表3 电机基本参数Tab.3 Basic Parameters of Motor

1.4.1 加速度校验

预计加速段要求速度在0.5 s 内将速度提升到2 m/s。卷扬机的加速度由牛顿第二定律可求得：

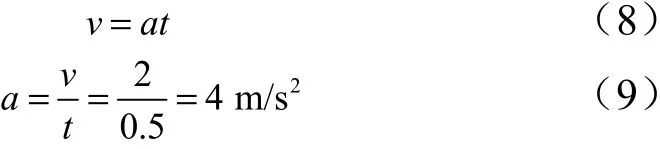
得出最小加速度为4 m/s，角加速度由式（10）和式（11）可计算出结果：

经计算角加速度为=20 rad/s。

经过减速器后转化到电机的加速度可由式（12）计算：

计算得=100 rad/s。

综上，预选电机的加速度均能达到要求。

1.4.2 扭矩校验

根据数值计算，水的阻力和加速段的加速度产生的惯性力约为200 N，根据绕绳子轮子=200 mm，扭矩应该为

经计算，扭矩为=40 N·m。

电机扭矩根据式（14）可求：

可得：=8 N·m。

预选电机的额定扭矩为：48 N·m。电机扭矩满足驱动系统要求。

1.4.3 转速校验

卷扬机的转速由式（15）和式（16）计算：

计算得=5 s，=6.38 m/s。

需求的最高速度为2 m/s，根据计算获得额定转速下的转速小于设备需要的最高速度，电机符合要求。

1.4.4 速度校验

减速器的调速范围0~10 Hz。速度由式（17）计算出结果：

计算得=12.56 m/s。

根据减速器计算的速度大于额定转速下的最大速度，因此，减速器和电机选择均符合要求。

2 试验及结果分析

2.1 试验环境搭建

试验过程中电机功率7.5 kW 伺服电机，电机转速3000 min，减速器减速比为=5，模拟发射平台的最大速度设定为1.2 m/s，匀速设定为1 m/s，试验过程中水深为2.5 m，顶端抽真空为3×10Pa，试验速度标定采用高速摄影标定方法，高速摄像机日本Photron高速摄像机，型号为：FASTCAM SA-Z，高速摄像采样率为5000 fps，高速相机距离测量水箱距离为3.5 m，发射平台质量为50 kg，弹丸质量为5 kg。

2.2 试验步骤

对建设的试验系统进行试验，试验方案如图6 所示。

图6 水平拖动试验Fig.6 Horizontal Drag Experiment

发射平台由于在水中移动，为防止编码器等测量设备进水导致速度测量不准确，本次试验中采用高速摄像机对发射平台移动速度进行测量标定，具体试验步骤如下：

a）将发射平台推到发射水箱最右端，在水箱内粘贴标尺（图6 中箭头所指示处），用于对比发射平台位置，标定发射平台运行速度；

b）关闭试验水箱舱门，打开注水开关，往水箱内注水至2.5 m 处；

c）对水箱上层空间进行抽真空，真空度至3×10Pa；

d）将水下发射平台发射速度触发开关与高速摄像机触发端口相连，设定高速摄像机采样速率；

e）启动水下发射系统自动按钮；

f）采用像素处理技术完成发射平台测量速度曲线的拟合。

2.3 试验数据分析

拖动系统设计调试完毕后，进行测试，通过对比高速摄像机采集的每张照片中的发射平台最前端位置与标尺的关系，建立发射平台位置数据表，由相间隔两张照片间的拍摄时间间隔，完成对发射平台发射速度的计算和拟合。得到曲线如图7 所示，经过试验验证，本系统安全可靠，能够满足需求。

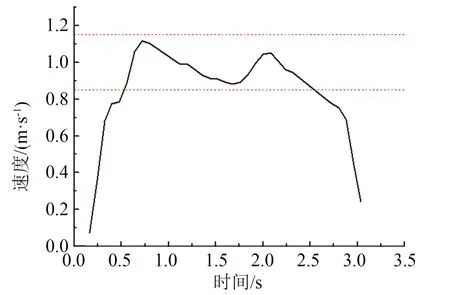
图7 拖动试验的速度曲线Fig.7 Speed-time Curve of Drag Experimental

从图7 中可以看出，速度达到设定最大值后出现减速过程，这是由于发射平台在移动过程中受水阻力作用，并且电机与发射平台之间采用柔性钢丝绳连接，待电机牵动钢丝绳速度达到试验时设定的0.8 m/s 的最大速度后，由于发射平台质量较大，惯性大，发射平台速度仍在上升，由于发射平台受水阻作用明显，速度逐渐减小，待发射平台速度重回0.8 m/s 后，牵引发射平台的钢丝绳变紧，发射平台速度重新上升，发射平台移动发射过程中钢丝上的松紧变化过程与拟合速度曲线过程一致，也说明采用伺服电机、卷扬机带动钢丝绳作为牵引动力的水下移动发射平台在速度上存在震荡过程，但是试验系统总体速度误差满足相关使用要求。

3 结 论

本文研究了实验室内的水下移动发射平台，重点介绍了试验系统的设计方案，建立 了发射试验系统的模型，通过ICEM 对模型进行了网格划分，运用Fluent软件仿真模拟了发射平台在水池中运动的受力情况，发现发射平台所受到的阻力存在震荡现象；根据受力情况和工程实际，采用伺服电机带动卷扬机的驱动系统方案，并完成驱动系统主要部件的选型和计算。最后，搭建了试验系统，进行了水下运动过程发射平台水平速度测量，验证了驱动系统设计满足使用要求。水下移动发射平台可以进行水下移动多弹发射试验，开展水下多弹发射过程中的空化、多弹干扰技术以及水下弹道控制等方面的研究工作。该试验平台的成功研制解决了室内水下弹丸移动发射试验难的问题，对室内水下发射技术的发展具有重要的应用价值和工程设计参考意义。