初中数学中的最短路径问题研究

刘静

摘要：初中数学是学生抽象性思维、发散性思维和逻辑性的重要培养阶段，而在初中数学知识中，“最短路径问题”就是一个既能锻炼学生数学思维，又能在现实中实践的数学问题。初中数学中的最短路径问题可分为两点之间最短路径问题、点与线之间最短路径问题以及立体几何图形上两点之间最短路径问题。本文就以上初中数学中的最短路径问题展开研究。

1回顾旧识，引入新知

回顾已经学过的理论知识，“两点的所有连线中，线段最短”、“连接直线外一点与直线上各点的所有线段中，垂直线段最短”等理论知識。引入最短路径问题，结合现实例子对两点之间最短路径、点线之间最短路径、立体几何中两点之间最短路径进行详细讲解。

2最短路径问题实例

2.1两点之间最短路径

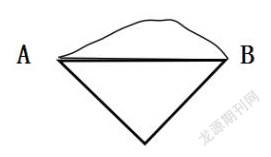
例：如图，已知有AB两点，两点间有三条线连接，求两点间的最短距离。

分析：显而易见，通过所学的知识“两点之间，线段最短”的知识便能很快知晓两点间的最短路径。同时也可引出三角形的三边关系“三角形的两边之和大于第三边”。这种问题在现实生活中最常见的应用是：选取两地之间的最短路线。

2.2点线之间最短路径

点线之间的最短路径问题中有一个点与一条线之间的最短路径、两点一线的最短路径、两点两线最短路径等问题。

（1）一个点与一条线之间最短路径问题

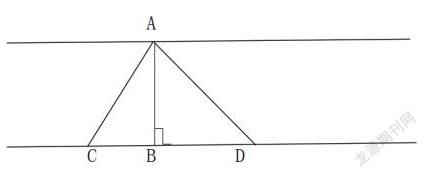
例：如图，小明开船想要从A点到河对面，问怎样走，路程最短。

分析：如图所示可知，小明想要从A点驾驶船只以最短距离到达对岸，只有按AB路线行驶，依据理论可知，点到直线上的所有线段中，垂直线段最短。

（2）两点一线的最短路径

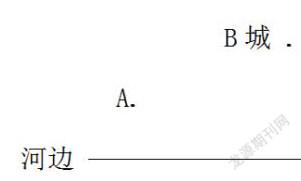
这个问题便是最经典的将军饮马问题，例：相传有位将军骑马从A地出发，要到河边去饮马，再然后去B城视察，问将军到河边的什么地方饮马可以使得其所走的全程路线最短。如图：

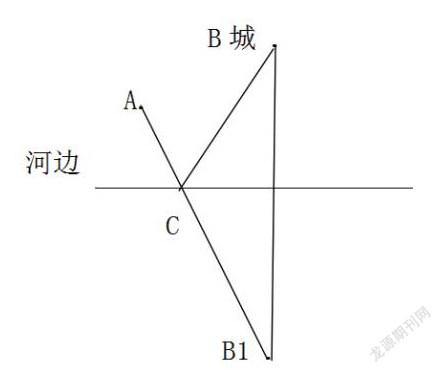
这个问题就非常考察学生对知识运用的灵活性，锻炼孩子的发散性思维。分析：以河边为对称轴，做出B城的对应点B1，根据轴对称的性质可知对称轴上任意一点C到B点和B1点的距离相等，所以AC+BC最短距离=AC+B1C最短距离，已知两点之间线段最短，连接AB1，相交于对称轴，可得点C，由此可得当C点为AB1与对称轴的交点时，将军所走全部路程路线最短[2]。如图所示：

2.3立体几何中两点之间最短路径

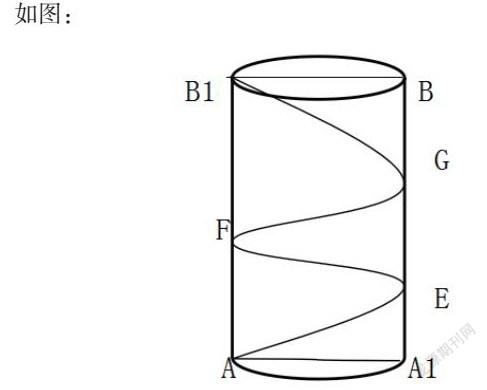
在立体几何求圆柱体上两点之间最短路径比较常见，是重难点所在。例：圆柱体底部直径为6cm，高为10cm，有只瓢虫在圆柱体表面如下图表示方法爬行，求其最短的爬行距离。

如图：

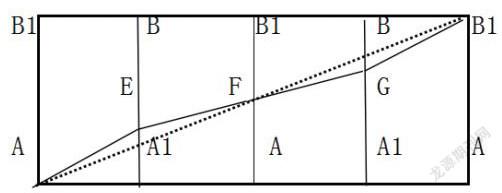
分析：可知圆柱体表面展开是一个长方形，由此将AB所在截面分成两个部分，那这条曲线就被分成首尾相连的四段，将曲线展开后将得到四个相等的长方形，于是将四段曲线变为线段，那由图可知，当所有线段为同一条线时，路径最短，即AB1的长度[3]。如图所示：

此题最为关键的地方在于，讲立体几何的数学问题转化为平面几何，将复杂问题简单化;此外还囊括了勾股定理，化曲为直等思想方法，所以这就要求学生一是要有扎实的理论基础，二是要将学习到的东西灵活运用于题目中。

参考文献：

[1]尹加根.解析数学教学中的最短路径问题[J].数学学习与研究，2018，17（09）：139.

[2]徐根宝.浅析初中数学最短路径问题[J]. 试题与研究：教学论坛， 2018（3）：50-50.

[3]吴高敏.柱体表面上的爬行（缠绕）最短路径问题探究[J]. 中学数学研究：华南师范大学， 2017（18）：46-48.