基于频移键控的仿海豚哨声水声通信技术

马天龙 刘凇佐 乔 钢 浦王轶

(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

(工业和信息化部海洋信息获取与安全工信部重点实验室(哈尔滨工程大学) 哈尔滨 150001)

(哈尔滨工程大学水声工程学院 哈尔滨 150001)

1 引言

随着水声通信技术的发展，除了可靠性、通信速率和网络化外，水声通信的安全性与隐蔽性也逐渐受到重视[1-3]。传统方法大多采用低检测概率(Low Probability of Detection， LPD)技术实现隐蔽水声通信，该技术通过扩频等方式降低通信信号的功率，将通信信号隐藏在海洋环境噪声中，使其难以被发现[4,5]。但是信噪比的降低会降低通信系统的性能，并且在信源附近通信信号信噪比较大，通信信号和声源易暴露，难以有效保证通信的隐蔽性[6]。与传统的LPD隐蔽通信技术不同，仿生水声通信利用海洋中固有的海洋生物叫声或者人工合成的模拟叫声作为通信信号，令敌方在检测到这些信号后，误将其识别为海洋生物叫声而排除，从而达到隐蔽通信的目的[7]。该方法不需要限制通信信号信噪比，即使通信信号被检测到，大概率也会被排除，可有效保证通信的隐蔽性和通信平台的安全性。综合分析声源时空特点和信号频率特征后，发现海豚叫声是一种适合模仿的海洋生物叫声[8,9]。

基于海豚叫声的仿生通信算法近年来受到广泛关注，根据调制方式可以将其分为两大类：一种是基于原始的海豚叫声，利用时延编码技术[7]、脉冲位置调制技术[10,11]、M元技术[12]或者这些技术的组合[13]将信息调制到叫声类别与时间位置上，以实现仿生通信。例如这类方法需要从采集样本中提取原始的海豚叫声，因此叫声样本的数量和质量严重影响这类方法的通信性能。另一种方法是利用与原始叫声(大多是海豚哨声)高度相似的人工合成模拟叫声作为通信载波，基于叫声的参数模型[14-17]或者数字水印嵌入技术[18,19]，将信息调制到模拟叫声的时频参数上以实现仿生通信。这类方法不受海豚叫声样本数量限制，信息调制更加灵活，应用潜力更大。

文献[17]提出一种基于海豚哨声时频谱轮廓的仿海豚哨声跳频(Frequency Hopping, FH)水声通信算法，该方法将信息调制生成的连续相位频率调制信号以一定的比例系数与海豚哨声信号时频谱轮廓相加，基于哨声信号模型产生合成哨声实现仿生通信。但是该方法需要在接收端产生每个码元所有可能的信号用于和接收码元进行相关，通过相关峰的大小进行判决解调，所需的运算量较大，调制解调算法较为复杂。针对这一问题，本文提出一种基于频移键控(Frequency Shift Keying，FSK)的仿海豚哨声信号水声通信算法。该方法以海豚哨声作为频移键控的载波，将经过处理后不存在跳变点的基带信号以一定比例与哨声信号时频谱相加，产生合成哨声用于信息发送。接收端同步后提取合成哨声，然后将其与本地存在频差哨声载波相干相乘，再经过低通滤波获得FSK信号用于解调信息，实现仿生水声通信。通过仿真与海试试验初步验证该方法的可行性，从时频相关系数和Mel倒谱系数评价通信信号的仿生效果，并结合误码率、通信速率对通信性能进行综合分析。

相较于文献[17]的仿哨声FH水声通信算法，本文所研究基于FSK的仿海豚哨声水声通信，或简称为仿哨声FSK水声通信，调制解调过程得到简化，系统资源消耗显著降低，为仿生水声通信算法的实际应用提供技术支撑。

2 仿海豚哨声水声通信算法

2.1 海豚哨声信号模型

2.2 调制算法

仿海豚哨声水声通信信号需模拟海豚哨声时频变化特性，因此需基于海豚哨声时频谱轮廓曲线进行调制。考虑到哨声信号的谐波可通过基波倍频获得，因此基波更具有代表性，故本文选取哨声信号基波时频谱轮廓曲线fw,1(t)用于介绍仿生通信调制解调算法，对于其它谐波的调制解调只需将所用哨声时频谱轮廓换成对应阶次谐波的时频谱轮廓fw,r(t)即 可。基于海豚哨声时频谱轮廓fw,1(t)的调制过程主要包括两个步骤：第1步对信源信息进行基带调制，产生基带信号；第2步则是将基带信号与海豚哨声信号时频谱轮廓曲线进行组合，再基于海豚哨声信号模型产生合成哨声，实现仿生调制，具体过程如下：

2.3 解调算法

接收端，利用海豚哨声信号sw(t)对接收信号进行同步，提取接收到的合成哨声rs(t)，然后将接收到的合成哨声rs(t)与本地产生的存在固定频差哨声信号sl(t)相干相乘，经过低通滤波后即获得频移键控信号rFSK(t) ， 最后解调频移键控信号rFSK(t)获得解调信息a*，具体过程如下。

图1 仿海豚哨声FSK通信频谱调制示意图

图2 仿海豚哨声FSK通信信号帧结构

海豚哨声信号频率随时间连续变化，相邻两个码元所在的合成哨声时频谱轮廓并不相同，由水声信道的多途效应导致的前一码元的干扰与当前码元在频谱上几乎不重叠或者重叠范围很小，因此仿海豚哨声FSK通信方法在不进行信道均衡的条件下也可有效降低多途信道带来的码间干扰。

文献[17]的仿哨声FH水声通信算法与仿海豚哨声FSK调制水声通信算法运算量的差异主要体现在接收端产生本地信号中。仿哨声FH水声通信算法在接收端需将接收到的每个码元波形与本地产生的该码元的所有波形进行相关运算，通过对比相关峰大小以实现解调。由于每个码元所对应的哨声信号时频谱轮廓不同，故在解调时每个码元的每种可能的波形都需要单独生成或存储，系统资源消耗较大。而仿海豚哨声FSK调制水声通信算法不需要针对每个码元产生不同的本地信号，接收端只需要产生或存储固定的信号：存在频偏的本地哨声sl(t)和对应FSK调制频率的单频信号，通过相干相乘和能量判决进行解调，系统资源消耗量显著降低。若采样频率为Fs，离散后的每个码元采样点数为Nc=T×Fs，每种码元包括M种可能性波形，每个合成哨声包含的码元个数为N，N×Nc≈Tω×Fs。则根据文献[17]，仿哨声FH水声通信算法完成一个合成哨声解调需要MN×4Nc次乘法、MN×(3Nc-2) 次加法和2MN次余弦运算，需要MN×Nc个存储单元存储所有可能的波形。而仿海豚哨声FSK调制水声通信算法则需要2Tw×Fs+2MNc+MN×2Nc次乘法、Tw×Fs-1+MN×(2Nc-1)次加法和M+1 次余弦、M次正弦运算，需要Tw×Fs+2MNc个存储单元用于存储本地哨声sl(t)和 FSK调制对应的M个单频信号。所以总体来看，仿海豚哨声FSK调制水声通信算法计算复杂度更低，对系统资源消耗更少。

本文主要考虑固定收发节点通信情境，对于存在多普勒的情况，假定一帧通信信号的多普勒因子不变，可利用原始的海豚哨声信号sw(t)在时延和频移2维平面上对接收通信帧中的海豚哨声信号进行搜索，获得该帧接收通信信号多普勒因子，再基于多普勒因子对接收通信信号进行重采样以降低多普勒效应对通信系统的影响。

3 仿真实验

3.1 海豚哨声信号

实验采用一段真海豚(Common Dolphin)的哨声信号作为仿哨声通信模拟对象，该哨声信号公布在Watkins Marine Mammal Sound Database数据库[21]，其波形和时频谱如图3所示。该哨声信号长度约为1.3 s，频谱清晰，可以明显看到基波和第2、第3次谐波。该哨声基波具有清晰的时频谱轮廓，最低频率约为9 kHz，最高频率约为16 kHz，频率随时间连续变化。基于文献[17]所述的时频谱轮廓提取方法提取该哨声基波时频谱轮廓，并略微调整其频率范围至8～16 kHz，用于后续仿海豚哨声水声通信实验。

3.2 仿真实验分析

仿真实验所用哨声时频谱为3.1节获得的真海豚哨声基波时频谱轮廓。仿真信道采用文献[22]的随机信道模型，该模型假定：水声多途信道可用一定数量的多径来表示，相邻的两条多径之间的时延差值服从均值为一定值的指数分布，每条多径的幅度服从瑞利分布，并且信道的平均功率随着多径时延的增加呈指数衰减。基于该仿真信道，仿真了不同码元宽度为T和调制频差Δf情况下仿哨声通信算法的性能，具体的仿真实验参数如表1所示。当码元宽度为0.1 s时，产生的合成哨声时频谱如图4所示。

表1 仿真实验参数

图4中，第1个为基于图3所示哨声基波时频谱轮廓产生的原始哨声时频谱，后续为不同调制频差Δf所对应的合成哨声时频谱。当Δf<50时，从时频谱上基本看不出合成哨声和原始哨声的区别。随着调制频差 Δf的增大，合成哨声时频谱变化越明显，与原始哨声的差异性越大，相应的通信信号仿生效果下降。当Δf=200时，可明显看出合成哨声时频谱轮廓存在突然变化。若增加过渡信号时长L，可令时频谱变化更为平缓，但是会减少每个码元在相应频率上的时长，影响FSK解调。

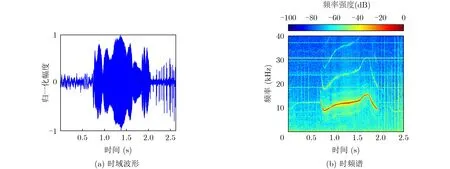
图3 真海豚(Common Dolphin)哨声

图5和图6为仿真实验的误码率曲线。图5和图6中蓝色曲线为仿哨声FSK通信算法误码率曲线，黄色、褐色和红色曲线为仿哨声FH水声通信算法的仿真结果[17]。从图5和图6可以看出，当码元宽度T一定时，增加调制频差Δf可以有效降低误码率，提高系统的可靠性。对比图5和图6，在其他条件相同时，相同误码率情况下码元宽度T为0.1 s时所需的信噪比比码元宽度T为0.05 s时要低4～5 dB。增加调制频差 Δf可增加FSK信号两个载波频率f1和f2上的距离，减少频谱混叠，而增加码元宽度T可以有效提高频率分辨率，两者都可以提高FSK解调性能。但是，增加 Δf会增大合成哨声时频谱轮廓变化，影响到合成哨声的仿生效果。

仿哨声FH水声通信算法将连续相位多载波频移键控(Continuous Phase based MulticarrierFrequency Shift Keying, CPMFSK)信号以一定比例系数k与哨声时频谱相加产生合成哨声时频谱，该合成哨声时频谱在每个码元时间内会在一定的频率范围内不停变化，其变化范围由调制系数k决定。而仿海豚哨声FSK调制水声通信算法采用2FSK调制信息，合成哨声频谱在每个码元时间内与原始哨声时频谱的频差保持不变，为固定值 Δf，如图4所示。从图5和图6的误码率曲线可知，当频谱最大差异一定时，即调制系数k与调制频差Δf相等时，仿海豚哨声FSK调制水声通信算法的误码率表现更好。当调制频差Δf=200时，仿海豚哨声FSK调制水声通信算法的误码率曲线与k=400的仿哨声FH水声通信算法基本重合，但是仿海豚哨声FSK调制水声通信算法频差更小，因此仿海豚哨声FSK调制水声通信算法仿生效果更强。

图4 码元宽度为0.1 s时合成哨声时频谱

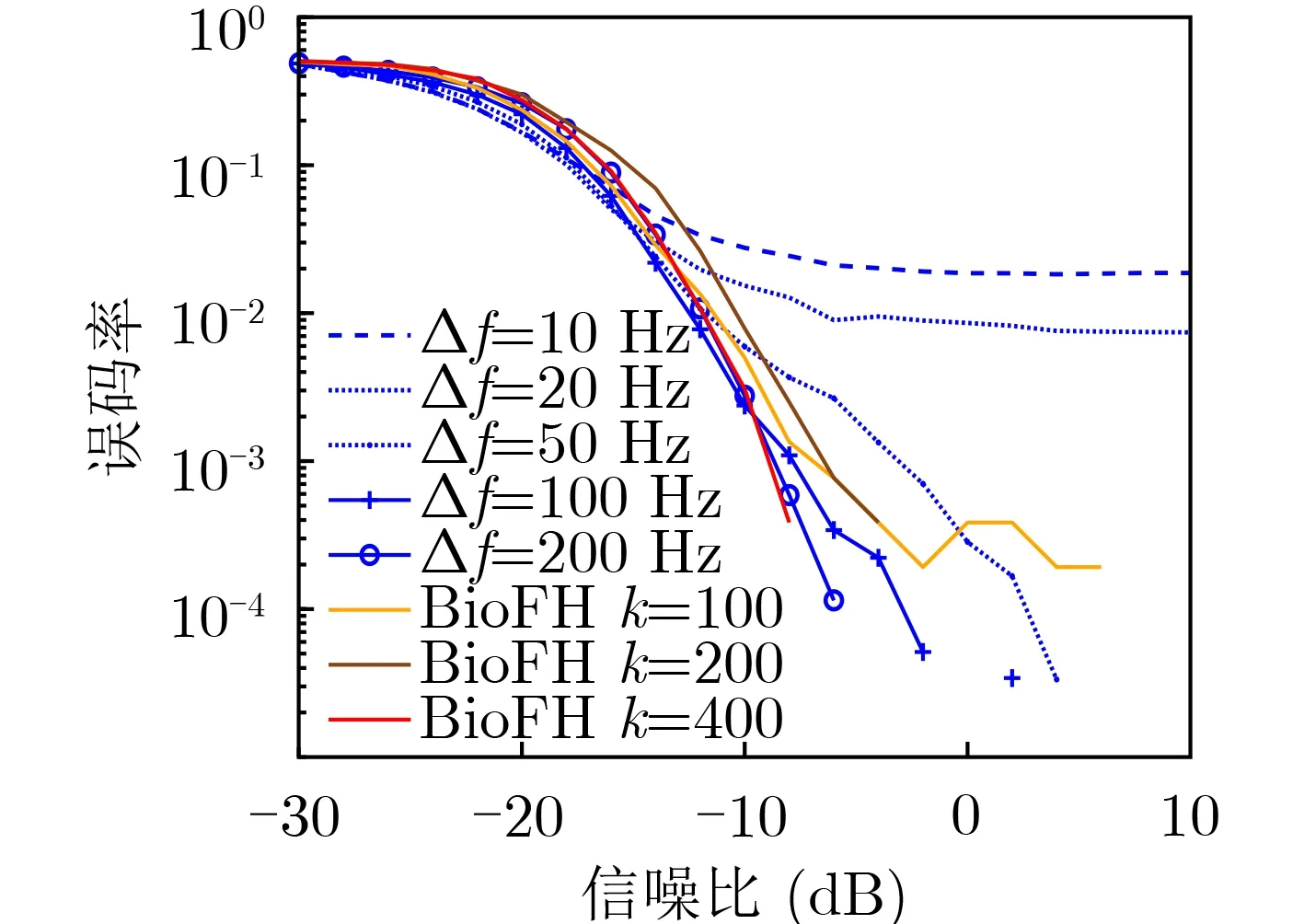
图5 码元宽度为0.1 s时误码率曲线

图6 码元宽度为0.05 s时误码率曲线

3.3 仿生效果分析

参考文献[17]，本文亦选用时频相关系数(TFCC)r和Mel倒谱距离(MelD)dMFCC对仿哨声FSK水声通信信号的仿生效果进行分析。基于表1的参数，每种参数分别产生了1000个合成哨声，计算其与原始哨声的时频相关系数和Mel倒谱距离，结果如表2所示。其中，计算Mel倒谱距离dMFCC时，选取的三角窗函数窗长为0.1 s，相邻帧的重叠长度窗长的一半，Mel滤波器个数为24个。

时频相关系数均值r¯越接近于1，Mel倒谱距离均值d¯MFCC越小，证明合成哨声和原始哨声差异性越小，通信信号仿生效果和隐蔽性越高。结合图4和表2不难发现，当码元宽度T一定时，增加调制频差 Δf会降低时频相关系数并增大Mel倒谱距离，即增加调制频差 Δf会降低通信信号的仿生效果；而当调制频差Δf一定时，增大码元宽度T可提高通信信号的仿生效果。总体来看，本文提出的仿海豚哨声FSK水声通信信号的仿生效果较好，各参数平均时频相关系数都在0.99以上，平均Mel倒谱距离不超过3.2。

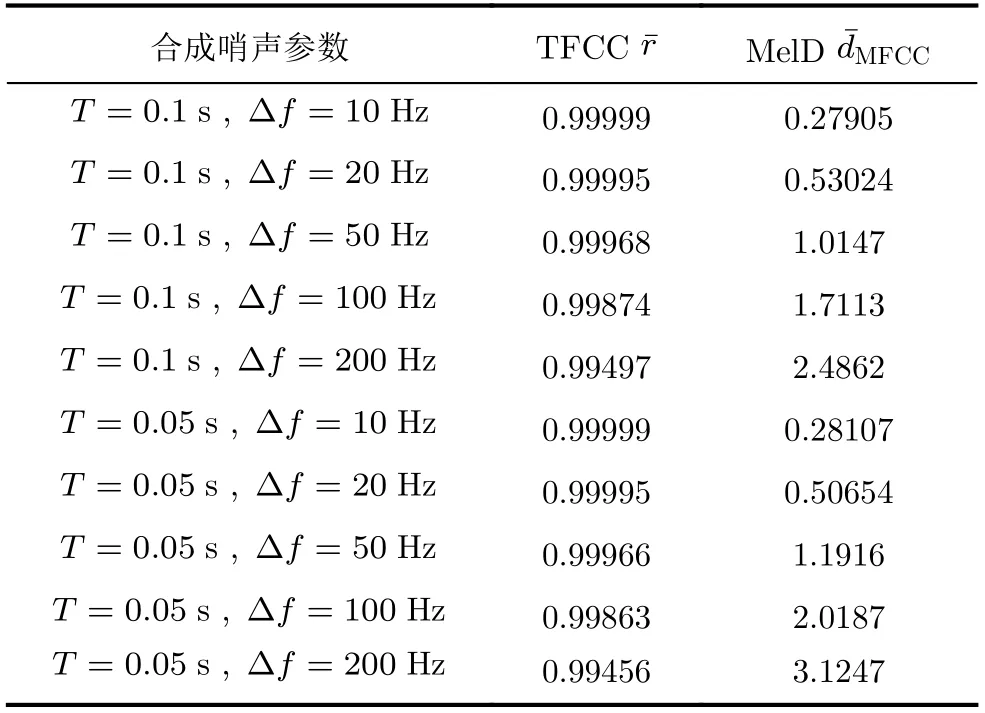
表2 仿哨声FSK通信信号相似度

表3为通信速率基本相同条件下，仿哨声FH水声通信信号[17]、分段LFM仿哨声通信信号[15]和基于数字音频水印技术的仿哨声通信信号[18]的仿生效果，其中，前两种仿生通信技术均基于哨声信号时频谱轮廓进行调制，与本文仿哨声FSK水声通信原理相同或相近。基于数字音频水印技术的仿哨声通信则将信息隐藏在宽带哨声频谱中，与仿哨声FSK水声通信原理不同，因此选用时域波形相关系数(WCC)代替TFCC描述通信信号波形相关性，所用哨声为文献[21]公布的一段长鳍领航鲸叫声，并选取其中部能量较高的0.6s时长叫声片段用于信息水印。对比表2和表3，相较于仿哨声FH通信信号，仿哨声FSK通信信号的时频相关系数更趋近于1，Mel倒谱距离更小，但是随着调制频差 Δf增大，两者Mel倒谱距离趋于相同。相较于分段LFM仿哨声通信信号，仿哨声FSK通信信号的仿生效果明显更好，根据文献[17]的分析，仿哨声FH通信效果与分段LFM仿哨声通信效果基本相同，结合3.2节的仿真分析，可推断本文提出的仿哨声FSK水声通信技术的通信效果，当调制频差Δf ＞50时，与分段LFM仿哨声通信效果也基本相同，但是仿哨声FSK水声通信信号的仿生效果更好。相较于基于数字水印的仿哨声通信，仿哨声FSK水声通信信号的TFCC和Mel倒谱距离与基于数字水印的仿哨声通信的WCC和Mel倒谱距离数值接近，结合文献[18]公布的误码率与3.2节的仿真分析，两者通信效果相近，当调制频差 Δf ＞50时，仿哨声FSK水声通信技术通信效果略好。综上，可初步论证本文提出的仿哨声FSK水声通信技术，在通信效果相近的前提下，通信信号仿生效果良好。

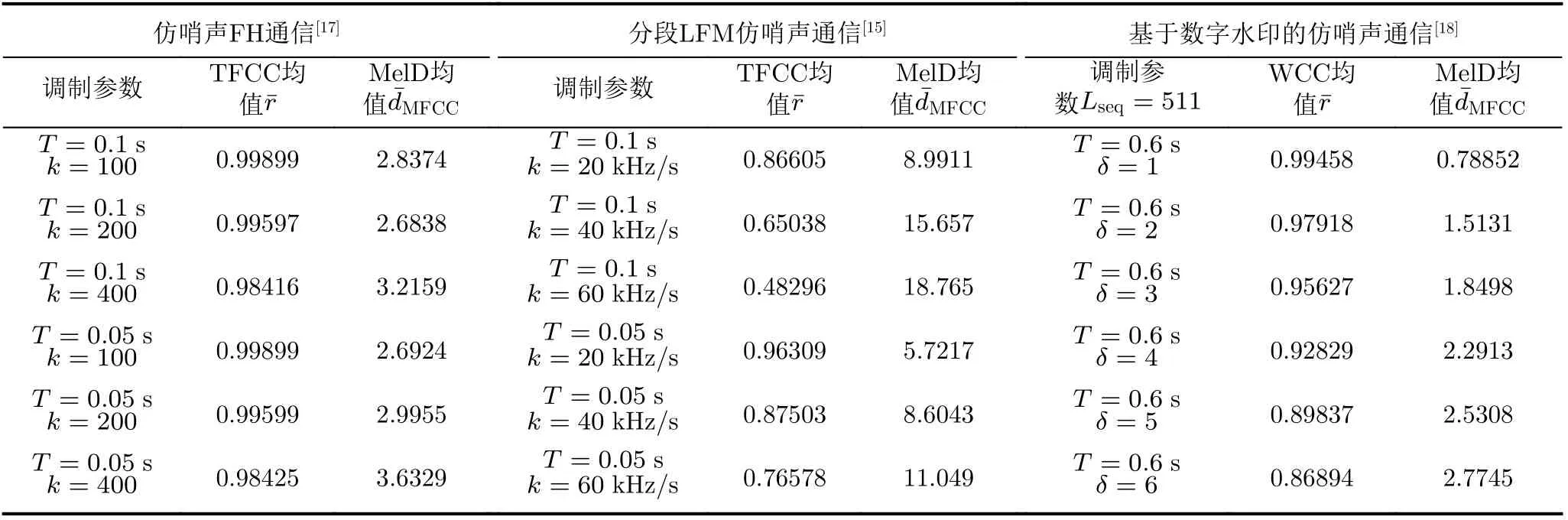
表3 基于仿哨声FH通信信号相似度

3.4 仿真结果综合分析

结合3.2节的误码率分析和3.3节的仿生效果分析，对本文所述的仿海豚哨声FSK水声通信算法性能进行综合分析。在该方法中，码元宽度为T和调制频差Δf是两个重要的参数。当码元宽度T一定时，增加调制频差 Δf可以有效降低误码率，提高系统的可靠性，但是通信信号的仿生效果会下降。当调制频差Δf一定时，增加码元宽度T可以在几乎不影响通信信号仿生效果的情况下有效降低误码率，提高系统的鲁棒性，但是系统通信速率会下降。因此，在进行参数选择时，需要综合预期的仿生效果、通信系统的速率和可靠性进行合理选择，优先满足预期的仿生效果，通过增加码元宽度T以牺牲通信速率为代价来提高通信系统可靠性。

对比本文所述的仿哨声FSK水声通信和文献[17]所述的仿哨声FH水声通信技术可以看出，在通信信号仿生效果相近的情况下，本文所述的仿哨声FSK水声通信算法的通信性能接近甚至略优于仿哨声FH水声通信算法，而仿哨声FSK水声通信算法的调制解调过程更为简单，系统资源消耗更少，因此仿哨声FSK水声通信算法更具有实际应用前景。

4 海试试验验证

为验证本文所述仿海豚哨声FSK水声通信方法的可行性，于2021年10月在中国山东威海楮岛附近海域进行了验证性试验。试验时，发射端位于码头，采用一个8～16 kHz宽带换能器发射信号，其吊放深度约为2 m。接收端位于发射端西北方向，距离发射端大约2 km，接收水听器深度约为4 m。试验海域平均水深约为10 m，周围有航行传播和水产养殖区。海试试验所用的信号参数如表4所示，每种参数发射一帧通信信号，每帧通信信号包含6帧合成哨声。当码元宽度为0.1 s时，海试接收到的哨声信号时频谱如图7所示。

从图7可以看出，试验海域噪声较强，存在许多脉冲噪声干扰，影响通信系统频带。海试接收信号信噪比并不高，且在8～10 kHz范围内有较强的能量衰减，该频段的信号基本淹没在噪声中。带通滤波后，接收信号总体信噪比在1～2 dB。海试试验的解调结果如表4所示。图5、图6显示，仿真实验中当信噪比不低于0 dB时，码元宽度T为0.1 s，调制频差 Δf不低于50 Hz可以实现误码率低于10-5的可靠通信，这一点在表4的海试结果中也得到了验证。当码元宽度T为0.05 s时，实现正确解调所需的信噪比较高，海试接收信号的信噪比较低，故而产生些许误码。尽管数据量较少，但是海试试验结果可初步验证仿海豚哨声FSK水声通信算法在真实海洋环境下具有可行性。

图7 码元宽度为0.1s时海试接收合成哨声时频谱

表4 海试验证试验处理结果

综合仿真实验和海试试验不难发现，仿海豚哨声FSK水声通信方法实现可靠通信所需信噪比不能低于0 dB，且当信噪比一定时，码元宽度T对系统的通信性能影响最大。减小码元宽度T会降低频率分辨力和信号能量，从而降低通信系统解调性能，此外减小码元宽度T还会降低通信信号的仿生效果，因此在实际应用时，应在满足通信速率和仿生效果的前提下尽量增大码元宽度T以提高可靠性。若需进一步提高系统通信速率，可以考虑利用多载波频移键控等方式提高每个码元所调制的信息量，或利用哨声的各次谐波进行信息调制。

5 结束语

针对水下隐蔽声通信的需求，不同于传统的低信噪比隐蔽水声通信，本文提出一种基于频移键控的仿海豚哨声水声通信算法，通过模拟海豚哨声以降低通信信号被截获识别的概率，以实现隐蔽水声通信。该仿生通信算法基于海豚哨声时频谱轮廓曲线，将信息调制生成的基带信号以一定比例与哨声信号时频谱轮廓曲线相加获得合成哨声时频谱，再基于哨声信号模型生成合成哨声，用于信息传输，接收端提取接收到的合成哨声，与本地基于哨声时频谱轮廓生成的存在固定频差的海豚合成哨声相干相乘，经低通滤波获得FSK信号进行解调以实现仿生通信。最后基于时频相关系数和Mel倒谱距离分析了通信信号仿生效果。仿真与海试试验验证了该方法的可行性，试验结果表明码元宽度T和调制频差Δf为影响系统性能的重要参数，当码元宽度T为0.1 s，调制频差Δf ＞50 Hz，信噪比不低于2 dB情况下，该方法可实现可靠通信，且此时通信信号的时频相关系数超过0.99，仿生效果较好。与仿哨声FH水声通信算法对比，本文所述仿哨声FSK水声通信算法在通信性能相近的情况下，调制解调过程得到简化，复杂度与运算量显著降低，更易于工程实现，为未来仿生通信的实际应用提供技术支撑。

接下来将继续进行外场试验，以综合分析验证该方法的性能，并进一步研究多元频移键控调制技术在仿生通信中的应用，以提高系统的通信效率。此外，尝试分析多普勒效应对仿生水声通信系统的影响，为仿哨声水声通信技术在移动通信中的应用做准备。