干扰输入影响下离散线性切换系统的反馈控制方法
黄丽琼,王园园
(1.商洛学院数学与计算机应用学院,陕西 商洛 726000;2.商洛学院电子信息与电气工程学院,陕西 商洛 726000)
0 引言
输出调节问题是当前切换系统输出控制的关键性问题之一,一般通过设计反馈控制器消除外界干扰。然而,由于切换系统是一类特殊的混杂系统,容易受到外界环境影响,存在系统稳定性差的问题。因此,离散切换系统的稳定性与反馈问题是切换系统理论研究的重要内容,除了强线性分析方法之外,在离散切换系统中,渐近式子系统的稳定运行仍是一个难点。为此,需控制离散线性切换系统。
文献[1]提出了基于平均驻留时间的反馈控制方法,该方法通过控制切换输出反馈控制器和对切控制器控制离散线性切换系统,该系统在每次切换时,都要执行复位操作,以保证每一个切换时刻的状态都能实时地控制系统输出结果,解决了切换系统输出的调节问题。文献[2]提出的基于切换原理的反馈控制方法,把刷新时间间隔作为延时变量,并将其转化为动态数据,实现不同子系统之间的数据切换,保证输出结果趋于稳定。上述2种方法受到外界环境干扰,导致控制效果不佳,因此,提出了干扰输入影响下离散线性切换系统的反馈控制方法。
1 离散线性切换系统分析
离散线性切换系统运行时,系统的控制层和输入层决定了系统输出结果,并且在该过程中,各个子系统在同一时间内只能激活1个子系统。因此,子系统的输入信号切换性能是决定整个系统的关键因素[3]。设定矩阵为对称正定矩阵,描述离散线性切换系统,即
x(k+1)=Aλ(k)x(k)+Bλ(k)u(k)+ω(k)
(1)
x(k)为离散线性切换系统输入状态;u(k)为离散线性切换系统控制输入;ω(k)为干扰输入;Aλ(k)、Bλ(k)均为常数矩阵;λ(k)为依赖于离散线性切换系统输入状态x(k)的切换信号[4-5]。由此构建的离散线性切换系统模型如图1所示。

图1 离散线性切换系统
由图1可知,该系统的切换稳定性不仅受到激活子系统影响,还受到切换规则的限制[6]。在整个信号切换过程中,一旦选择的切换规则不当,就会导致整个切换系统不稳定[7]。
基于上述系统,设定2种情况:
a.离散线性切换信号是唯一的。
如果外部干扰是存在的,则干扰信号ω(k)输入需满足
ω(k)Tω(k)≤Z
(2)
其中,Z≥0为常数。
b.离散线性切换信号是任意的。
如果外部干扰是不存在的,则离散线性切换系统可表示为
x(k+1)=Aλ(k)x(k)+Bλ(k)u(k)
(3)
充分考虑上述2种情况,设计线性切换状态下的反馈控制器,即
(4)
分析所有可能影响系统的切换序列,判断其稳定条件,这对系统的反馈控制具有重要影响[8]。
2 基于输出反馈的鲁棒镇定控制研究
2.1 输出反馈的问题描述
在干扰输入影响下的离散线性切换系统是一个动态切换过程,被控对象描述为
(5)
Cλ为常数矩阵;Sc为被控对象。假设被控对象在kT+tik时延下采集到的输入信号为u(kT+tik),i=1,2,…,p,经过零阶保持器处理后,能够产生一个连续信号u(t),即为被控对象的输入信号[9]。零阶保持器在信号处理过程中,能够保持刷新时间不变[10]。
结合离散线性切换系统实际应用情况,简化信号非统一输入过程,详细内容为:
a.实际上在不均匀输入过程中,输入信号一般具有时滞性,当前输入信号与过去的历史信号是相关的,即
u(kT+tik)=u(kT-ZT)
(6)
为了计算方便,Z取整数;T为输入周期。
b.产生的连续信号,可表示为
(7)
其中,τk为刷新时间,也是时延。
c.输入周期是由N个最小周期T0组成的,可表示为
T0=T/N
(8)
由式(8)可知,零阶保持器HΓ存在固有的刷新周期。
上述3点在实际不均匀输入系统中是常见的,如离散线性切换系统的延迟、切换时的信号交换延迟等[11]。
2.2 切换过程分析
通过描述输出反馈的问题可知,时延变化范围为0≤τk≤T,在任意切换时间内,都存在2个控制量,分别为u(kT)和u(kT-T),将这2个控制量同时作用于被控对象,由此得到的控制信号时序,如图2所示。

图2 控制信号时序
由图2可知,控制信号u(k)经过时延τk=t1-kT后,到达零阶保持器端,零阶保持器在kT+3T0时间范围内读取输入值,将u(k-1)更新为u(k)[12]。
针对任意k>0的输入值,将u(kT)和u(kT-T)这2个控制量同时作用于被控对象,作用的时间分别为n0(k)T0和n1(k)T0,则有
(9)
n1(k)值与时延大小有关。对式(9)进行离散化处理时,应充分考虑时延大小,离散线性切换模式的2个输入矩阵与n1(k)和n0(k)大小有关[13]。当离散线性切换模式具有多变性时,说明n1(k)和n0(k)的值不一致;当离散线性切换模式具有唯一性时,说明n1(k)和n0(k)的值一致[14]。因此,式(9)可视为子系统数目有限的切换系统[15]。
2.3 反馈控制流程设计
2.3.1 降阶控制律设计
为了使离散线性切换系统渐近稳定,设计了降阶控制律,使其具有加权增益性能。假设α为系统的切换信号,[t1,t2]为时间间隔,Nα(t1,t2)为切换次数。
对于任意条件N0≥1,τa>0,则有
(10)
τa为平均驻留时间;N0为活动界限。

2.3.2 有限时间镇定反馈控制
通过构造一阶输出反馈律,设计干扰输入影响下的有限时间镇定反馈控制方案。在离散线性切换系统切换过程中,由于离散线性切换系统受到外部环境的干扰,会产生延迟和丢包现象。
以下是通过缓冲器的信号与信号是否传输成功之间的关系,即

(11)


(12)
假定对切换系统作出如下假设:
a.时延小于系统的切换周期。
b.以时间驱动方式,保持切换周期一致。
c.在切换过程中,信号可能随时出现丢失情况,且信号丢失情况一般存在上界。
在假设条件下,若存在对称矩阵,则S>0;如果存在变量代换矩阵Y,则实数γ≥1,则有
(13)
因此,状态反馈控制器可以用离散线性切换系统来表示为
u′(k)=YS-1x(k)
(14)
在式(14)下,离散线性切换系统处于有限时间稳定状态。
3 仿真实例
设考虑被控对象为
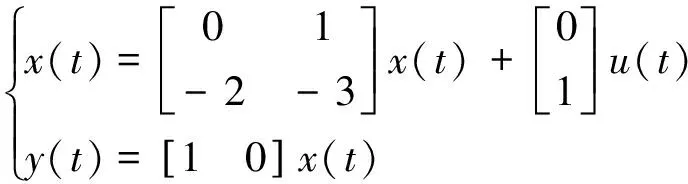
(15)
采样周期为10 ms,将采样周期均等分为10份,每份为1 ms,控制器可表示为
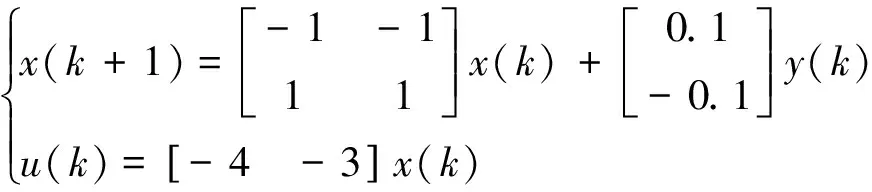
(16)
假设控制器工作的最大时延为4 ms,输入5种输入信号时延的取值情况,即τ(k)∈{0,1,2,3,4},也说明离散线性切换系统存在5个子系统。用Sci(i=0,1,2,3,4)表示这5个子系统,对应的输入矩阵都是由n1(k)和n0(k)决定的,相应的取值依次为[0 10],[1 9],[2 8],[3 7],[4 6]。
当时延为0时,Sc0为闭环采样系统模型;当时延发生改变时,Sc1为闭环采样系统模型。结合LMI的可行解问题解算器feasp,确定对称矩阵的可行解,即
上述得到的解满足输入条件,即指数衰减率满足最小解,因此,输出反馈控制器能够使离散线性切换系统保持稳定,仿真结果如图3和图4所示。

图3 系统x1(k+1)输出

图4 系统x2(k+1)输出
在图3和图4中,模拟结果显示,系统明显收敛到0,且是逐渐稳定的,由此也说明在满足切换条件下,离散线性切换系统输出指数稳定。
为了证明所研究方法的有效性,在最大时延6 ms情况下,输入7种输入信号时延的取值情况,τ(k)∈{0,1,2,3,4,5,6},也说明离散线性切换系统存在7个子系统,与此对应的x1(k)、x2(k)响应曲线,如图5所示。

图5 最大时延上界为6 ms的控制情况
由图5可知,x1(k)、x2(k)输出指数呈负线性相关关系,在时间为0~100 s时,x1(k)输出指数变化范围为0.10~0,x2(k)输出指数变化范围为-0.10~0。在时间为100~300 s时,x1(k)、x2(k)输出指数一致,均为0,趋于稳定状态。
基于此,分别使用平均驻留时间的反馈控制方法、基于切换原理的反馈控制方法和基于输出反馈的鲁棒镇定控制研究方法,对比分析x1(k+1)、x2(k+1)响应曲线变化情况,如图6所示。

图6 3种方法x1(k+1)、x2(k+1)响应曲线变化对比
由图6可知,使用平均驻留时间的反馈控制方法,在时间为0~300 s时,x1(k+1)输出指数变化范围为0.10~-0.02,x2(k+1)输出指数变化范围为-0.10~0.02,相交点为100 s,此时x1(k+1)、x2(k+1)输出指数均为0;使用基于切换原理的反馈控制方法,在时间0~300 s时,x1(k+1)输出指数变化范围为0.10~0,x2(k+1)输出指数变化范围为-0.10~0,相交点为150 s,此时x1(k+1)、x2(k+1)输出指数均为0;使用基于输出反馈的鲁棒镇定控制方法,在时间为0~300 s时,x1(k+1)输出指数变化范围为0.10~0,x2(k+1)输出指数变化范围为-0.10~0,相交点为100 s,与实际最大时延上界为6 ms的控制情况一致,说明使用该方法反馈控制效果较好。
4 结束语
本文提出了一种用于求解具有平均停留时间的切换离散线性内容的降阶控制律,将控制问题引入到综合控制问题中,并在统一的框架下建立了具有保证稳定性和最佳加权增益性能的降阶控制器。

