基于响应面法的爬壁机器人多目标优化设计

仲昭杰，刘芳华，孙天圣，狄 澄，吴万毅

(江苏科技大学机械工程学院，江苏 镇江 212100)

0 引言

船体清洁机器人的工作是在近似垂面的船体壁面上清除附着物，其吸附功能作为主要功能，值得重点研究。通常根据实际负载需要，选择足式、轮式和履带式作为行走机构，而吸附机构有负压吸附、永磁吸附、电磁吸附和推力吸附[1]。机器人在经过焊缝时由于受到自身载荷与外界因素的原因，机身会发生一定的形变量，故对机器人机身进行结构优化是需要迫切解决的问题。文献[2]提出一种基于Box-Behnken响应面法与有限元相结合的轻量化设计方法。文献[3]以质量最小和扭转刚度为优化目标函数，经过多目标优化后对比白车身的基础性能，使其达到轻量化目的。文献[4]基于结构应力和质量响应面模型，对结构质量进行求解，并通过数值仿真和实验测试对优化方案进行可靠性分析。文献[5]提出一种基于组合加权法设定子目标权重系数，通过拓扑优化使材料更加合理分布。文献[6]针对结构中存在的不确定性，提出了具有区间不确定性参数识别的分步实施方法，通过质量-弹簧系统数值算例与镜架系统实例，验证方法的可行性与可靠性。文献[7]使用DOE和响应面法技术对飞机机翼进行优化设计，减少机翼应力和结构整体质量。文献[8]基于响应面法得到结构变量和性能指标，计算出螺旋分离器最佳点的最大分离效率。

本文以爬壁机器人机身为研究对象，将机器人机身经过焊缝时的静态性能作为优化目标，在参数相关性与响应面分析的基础上，采用多目标遗传算法优化[9-10]，计算量小，效率高，满足提高机器人结构性能的要求。

1 爬壁机器人机身静态特性有限元分析

1.1 机身有限元模型的建立

工作过程中，爬壁机器人的模型材料对性能产生较大影响，为提高机身机械性能，材料选用质量轻、耐腐蚀、强度高的常用铝合金6061型号，其材料力学性能如下：密度为2 700 kg/m2，弹性模量为69 GPa，泊松比为0.33，屈服强度为275 MPa。

采用SolidWorks软件建立机身三维模型，主要由底盘和侧挡板组成，机身部分安装元件，同时作为承载部分承受推进器、清洗装置等部分的重量，通过螺栓与侧挡板连接。由于螺栓、圆角、倒角和孔等特征对机身的静态特性影响较小，故对模型进行简化，并通过设计变量参数化直接输出到Workbench中，可避免参数传递发生错误。对机身进行网格划分，网格大小为4。

1.2 有限元结果分析

机器人在爬行过程中遇到焊缝时，此时机器人履带状态为一侧不动，将其设置为固定约束，另一侧受到1个向上的支持力，载荷设置为20 N，同时机身的底盘受到元器件的所产生的重力，载荷设置为50 N。在经过焊缝时，受到支持力载荷的一侧发生较大的形变，位移形变最大值为0.63 mm；侧挡板镂空部分与底盘中间都有较大的应力产生，最大值为7.91 MPa。

2 机身响应面建模

2.1 DOE试验设计

试验设计的目的就是通过可调控因素来达到控制指标的目的。拉丁超立方抽样属于蒙特卡洛模拟法的一种，通过改进采样策略做到以较小的采样规模获得较高的采样精度，减少了迭代次数。本文提出一种基于参数敏感性筛选与拉丁超立方试验相结合的试验设计方法，提前对变量进行筛选。根据变量的敏感度高低进行不同水平的分层拉丁立方抽样，可以剔除参数中对于响应面目标影响较小的参数，以减少响应面构建或者直接优化过程中的计算量。自定义初始变量如表1所示。

表1 自定义初始变量

L1为底盘的宽度;L2为底盘的长度;L3、L4、D1分别为侧挡板中心圆距离、大小以及拉伸厚度，参数变化取值范围为±10%。

灵敏度的数值反映设计变量对响应性能的影响，灵敏函数为

(1)

s为试验目标uj对设计变量xi的敏感度系数。

假设有高低敏感度变量(m维)的水平数(P)和样本数目K(P≤K)。对于其余n-m维变量，划分为K个区间，在每个区间进行等概率抽样，抽样概率为1/K。为确定各区间内样本点数的具体位置，在[0,1]内产生随机数Ui(i=1,2,…,K)，与第K个区间对应的随机数UK为

(2)

相关性分析是指对2个或多个具备相关性的变量进行分析，从而衡量2个变量因素之间的密切关系。在参数相关性分析中，采用Spearman分布，过滤值为0.5，平均值为0.01，标准偏差为0.02，抽取40个样本点进行参数敏感性分析。如表2所示，可以得到底盘的宽度L1对最大位移变形T1影响较大；侧挡板中心圆大小L4对机身质量M影响较大；侧挡板拉伸厚度D1对等效应力T2影响较大。筛选出参数L1、L4、D1作为设计变量进行目标优化，这3个参数对机身的静态性能提升相对较大，或对轻量化设计影响较大。其中，L1上下限分别为528 mm、432 mm；L2上下限分别为66 mm 、54 mm；D1上下限分别为11 mm、9 mm。

表2 参数相关性表

试验设计方法为一种基于参数敏感性筛选与拉丁超立方试验相结合的采样方法，产生样本点为15个，如表3所示，相比较直接采用拉丁超立方试验抽取的100个样本点，大大减少了计算量。

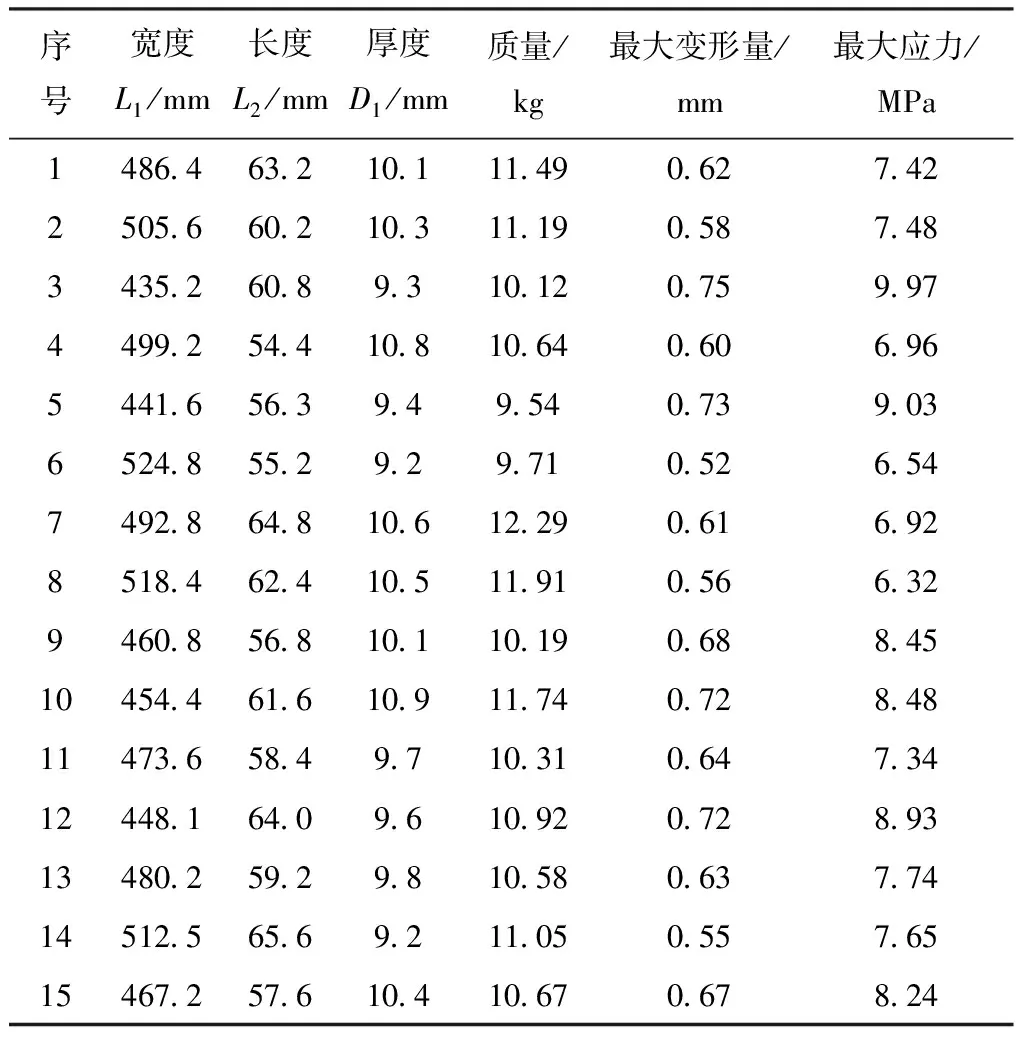
表3 拉丁超立方试验设计数据

2.2 响应面模型的构建

响应面优化法考虑试验随机误差，利用合理的试验设计方法通过试验得到一定数据，通过采用多项式回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最优工艺参数。二次响应面的回归方程为

(3)

β为二阶多项式响应面的拟合系数；xj、xj为设计变量；ε为误差项；n为设计变量个数。

通过对试验设计矩阵数据的多元回归分析，最终得到了拟合曲线。如图1所示，给出了基于样本空间设计点的2阶多项式响应面拟合曲线图，通过曲线可以看出，不同目标变量的响应面预测值随设计点的变化呈斜率为1的线性变化，3个优化目标中，最大等效应力的实际值偏离预测值有一定偏差，而质量与最大位移变形基本上与预测值符合。

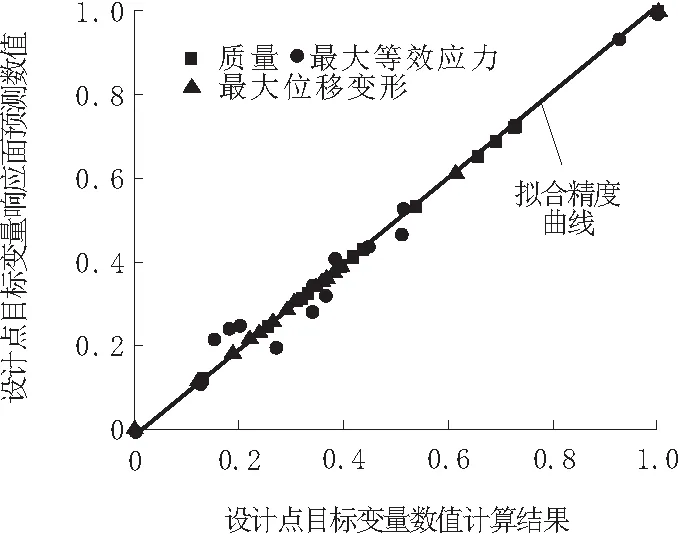
图1 响应面模型拟合度曲线

采用标准二阶响应面建模，通过Central Composite Design中心组合设计试验法建立响应面模型。响应面模型如图2所示，其中， 图2a为底盘宽度、侧挡板中心圆大小与机身质量之间的响应模型，可以看出质量随着底盘宽度的增加而增大，而随着中心圆直径变大，质量则逐渐变小；图2b为底盘宽度、侧挡板拉伸厚度与位移变形之间的响应模型，可以看出随着底盘宽度增大而位移变形减小；图2c侧挡板中心圆大小、侧挡板拉伸厚度与等效应力之间的响应模型，可以看出在中心圆直径大小在55～60 mm之间，等效应力随中心圆直径增大无明显变化，维持在7.5 MPa左右。

图2 响应面模型

2.3 响应面质量评价

选择标准二阶响应面构建，拟合度是指根据15组样本点所得到的标准二阶响应面表达式是否满足系统的评判标准，拟合精度只是代表响应面的样本点表达式的满足情况，并非是指所建立的响应面模型是符合真实的设计变量与响应目标之间的关系。

(4)

(5)

(6)

表4 质量评价

3 爬壁机器人机身优化设计

3.1 多目标优化设计数学模型

目前，对机器人实现轻量化设计主要通过采用新型材料减小质量，使最大位移变形最小和最大应力承受力最大，结构优化包括尺寸、形状优化，目标函数、状态变量和设计变量都是预定义好的。则多目标优化问题可描述为：设b1,b2,…,bs为设计变量，则模型的总重量M、最大位移变形T1、最大应力T2均为b1,b2,…,bs的函数。

目标函数为

F(b1,b2,…,bs)

(7)

F为关于设计变量b1,b2,…,bs的误差泛函。

总重量约束为

(8)

最大位移变形约束为

(9)

最大应力约束为

(10)

变量选值范围为

(11)

F为目标函数，由s个单目标函数组成；εi为设计变量上下限差值的绝对值。

在进行优化时，系统将所建立的响应面表达式传递到优化模型当中，采用MOGA多目标遗传优化算法，即NSGA-Ⅱ，第二代非基因支配策略的遗传算法，该方法需要计算的样本数较少，且通过分析计算可得到Pareto最优解可行域。初始种群生成3 000个样本，每次迭代600个样本，最大允许遗传代数为20代，其中变异系数为0.01，交叉系数为0.98。最大允许Pareto比例设置为60%，收敛稳定性设置为2%。通过多目标遗传算法与帕累托法进行计算后，获取3个Pareto最优解，如表5所示。

表5 Pareto最优解

将强量化作为首要优化目标，3组候选点中选择第1组，优化后质量大小为9.51 kg，最大变形量为0.53 mm，最大应力为6.55 MPa。由于侧挡板中心圆大小与拉伸厚度均变小，所以在保证轻量化与最大位移变形较小的情况下，使等效应力变小，属于正常现象。

3.2 模态分析

爬壁机器人在船面上行驶经过焊缝时由于受到船面不平整产生的激励，履带一侧受到向上的支持力，致使整个机身产生振动，若是机器人本身产生的固有频率接近船面激励频率，则会发生共振现象，长期这样会发生安全隐患，故要求机身低阶模态频率必须高于或低于船面激励频率。

这里将整体机身看作为简支梁，利用模态分析经验方程得

(12)

将其作为模态方程的解，导出振型方程及固有频率，即

(13)

联立得到底盘的固有频率为

(14)

设置为零约束，由于前6阶频率近似趋近0，选择第7阶与第8阶模态振型分析，得到模态振型如图3所示。通过模态分析可知，图3a与图3c第7阶模态为扭转状态，机身两侧沿Z轴扭转，底盘中间部分刚度较强，振型表现较弱，而侧挡板两端振型较为明显，优化前固有频率为21.48 Hz，优化后固有频率为26.32 Hz；图3b与图3d第8阶模态为弯曲状态，沿XOY平面弯曲，侧挡板与底盘接触部分刚度较小，振型表现较为明显，优化前固有频率为35.48 Hz，优化后固有频率为40.86 Hz。即扭转模态固有频率增大22%，弯曲模态固有频率增大15%，静态性能得到明显改善。

图3 机身第7阶、第8阶模态振型

3.3 优化前后性能对比

经过设计变量参数相关性分析，从5个设计变量筛选出3个灵敏度较高的参数，说明侧挡板的形状与厚度对机器人在经过焊缝时的基础性能影响较小。经过多目标优化后，底盘宽度增加，侧挡板的参数都是相对减小，优化结果为机身质量减少1.7 kg，最大位移变形减小0.1 mm，最大等效应力减少1.36 MPa。如表6所示，总的来说，机身的基础性能的变化比例控制在较小的误差内，说明即使不改变材料的前提下，也可以实现机器人的轻量化与结构性能优化。

表6 优化结果对比

4 结束语

a.本文提出一种基于灵敏度分析筛选的拉丁超立方试验的结构优化设计方法，通过筛选灵敏度较高的变量作为新的设计变量，能够大大减小计算量。

b.建立包括最大位移变形、最大等效应力和机身质量的响应面模型，对响应面模型进行质量评价时，复相关系数R2都是等于或者趋近1，模型精度高。

c.采用非支配排序遗传算法对机器人机身进行多目标优化设计，在不改变模型材料的前提下，机身质量减少1.7 kg，最大位移变形减小0.1 mm，最大等效应力减少1.36 MPa。

d.对比机器人机身的第7、8阶模态，在进行结构优化后，扭转模态固有频率增大22%，弯曲模态固有频率增大15%，避免机器人在经过焊缝时发生激励共振现象。