棒束子通道湍流交混特性的数值模拟研究

张 锐，马在勇，陆定晟，何清澈，张卢腾，孙 皖，潘良明

(重庆大学 低品位能源利用技术及系统教育部重点实验室，重庆 400044)

反应堆堆芯棒束燃料组件内部流动传热特性影响着堆芯相关热工参数，子通道间湍流交混效应使得通道内临界热流密度(CHF)提高。研究反应堆堆芯棒束子通道间湍流交混效应有助于提高反应堆的安全性和经济性[1]。

子通道间的湍流交混效应是一种由多因素(通道间压差、几何结构和机械部件等)导致的一种综合性交混效应[2]。国内外学者针对子通道间湍流交混效应展开了大量研究。王正杰等[3]通过无因次分析方法得出了描述子通道间单相湍流交混率的无因次方程式，并通过示踪法实验结果计算了近似方形排列的子通道单相湍流交混率以及无因次方程式的系数和指数。康森厚等[4]推导出了对任何形式排列棒束子通道皆适用的单相湍流交混无因次通用方程。曹念等[5]采用带格架的5×5全长棒束开展子通道单相交混系数实验研究，使用子通道分析程序配合实验数据间接获得了单相交混系数。谢峰等[6]对19根棒束绕丝结构燃料组件进行实验，并结合子通道程序计算得到湍流交混系数。张琦等[7]对5×5螺旋十字型棒束(HCF)组件进行热工水力实验，基于能量平衡法对HCF组件的交混特性进行了分析，发现HCF组件的等效交混系数不随雷诺数的增加而明显变化，其均值为0.019。Kawahara等[8]提出了一种用于预测核燃料棒束子通道间气液两相湍流交混率的弹状-搅混流模型，并用湍流交混率数据证实了该模型的有效性。Sharabi等[9]研究了几种湍流模型在非圆截面通道内的传热预测能力，并通过实验比较了湍流模型用于预测观测现象的性能。Wang等[10]提出了计算流体力学方法在反应堆工程中面临的主要挑战和发展方向，有利于推动其进一步应用。Ju等[11]提出了一种结合高通滤波大涡模拟(LES)模型的高可扩展高性能谱元方法，用于模拟单相工况下通过平行壁面通道和矩形排列棒束通道中的湍流流动，并通过实验和理论验证了湍流交混系数依赖于雷诺数的模拟结果，证明了谱元法结合LES模型的可行性。于意奇等[12]运用CFD方法对稠密栅元内典型子通道湍流流动进行RANS和URANS模拟分析，分析比较不同湍流计算模型特性。李小畅等[13]对无格架和带交混翼格架的5×5棒束进行数值模拟分析，通过计算在不同工况下的努赛尔数及流体湍流强度，对不同湍流模型的影响及近壁面网格处理的适用范围进行了比较分析。王雅峰[14]基于CFD数值计算理论对不同节径比和不同雷诺数的流体湍流工况状态进行了数值模拟，从而得到横向交混率的计算公式。对于不同子通道结构，裸棒束与带混合叶片的棒束也有相关研究，In等[15]通过一系列CFD模拟，分析了带搅混翼格架的全加热棒束的强化传热，与已有的实验数据进行了比较，并进行了相关分析。Ikeno等[16]对裸棒束内湍流流动进行了大涡模拟，分析了方形排列棒束内的湍流流动，并表明CFD的重要作用之一是利用湍流模型模拟流动中的物理现象，以及预测平均流动。Ju等[17]采用LES和非定常RANS(URANS)方法的谱元法研究了反应堆堆芯中带有定位格架和搅混翼格架的棒束中的湍流，通过将湍动能等值线与横向速度矢量相结合，研究了搅混翼格架形成的涡流行为，揭示了涡流行为。

上述研究表明，对于子通道间湍流交混效应的研究是非常有必要的。目前对子通道间湍流交混效应的实验研究主要是通过化学示踪剂方法来完成，这种方法只能得到局部点或面的参数，无法得到全局参数，同时进行实验需要消耗巨大的人力、物力和财力。为此，本文拟采用CFD方法对子通道间的湍流交混效应进行数值模拟研究。

1 数值计算模型

1.1 实验本体建模

本文以方形棒束排列的相邻两个子通道作为研究对象，采用DesignModeler软件建立节径比(P/D)为1.326的几何模型。燃料棒外直径(D)为9.5 mm，节距(P)为12.6 mm，轴向流动方向长度为800 mm。流动横截面如图1a所示，几何模型在横截面上网格划分情况如图1b所示。

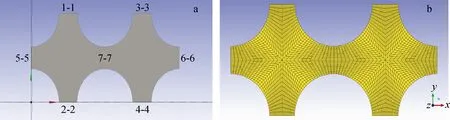
图1 流动横截面(a)和网格划分(b)

本文选择单相液态水作为工质，设定两子通道入口水温分别为300 K、320 K，子通道温度平均值对应物性参数，即密度ρ=992.5 kg/m3，动力黏度μ=7.02×10-4Pa·s，导热率λ=0.6 W/(m·K)，求解单相工况下对应的湍流交混系数。

1.2 网格敏感性验证

采用ICEM软件进行几何模型的网格划分。保持z方向长度4 mm不变，流动横截面网格采用相同划分方法，通过不断加密z方向节点数量得到4套网格。表1列出4套网格划分情况，采用M1、M2、M3、M4 4套网格分别进行完全相同工况下的数值计算，通过分析计算结果实现网格敏感性验证。

表1 网格数量对比

采用入口速度u=1.5 m/s，其他条件不变，计算对应工况流体速度分布及壁面切应力分布。为保证流动充分发展，取z=0.75 m处流动横截面上直线L1处的速度分布以及中心位置燃料棒与流体交界的圆弧R1上的应力分布，L1与R1位置如图2所示。图3示出M1、M2、M3、M4对应L1位置速度分布与R1位置壁面切应力分布。

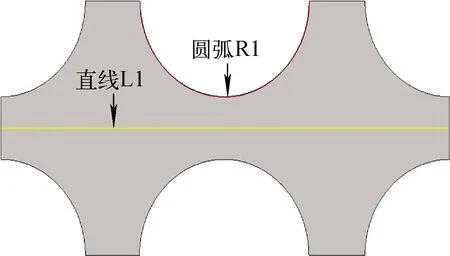
图2 R1与L1位置示意图

图3 L1位置速度分布(a)与R1位置壁面切应力分布(b)

由图3可知，4种网格计算所得L1位置处的速度分布变化趋势一致且数值上差别不大，而R1位置处的壁面切应力分布变化趋势基本一致，但数值上有所差别。M1与M4最大相差近5%，M2与M4最大相差近4%，而M3与M4之间数值上非常接近，相差程度都在1%以内。因此通过R1位置处的壁面切应力分布比较，可得出当网格数量在154万以上时计算结果已与网格数量无关，故选择M3网格进行数值模拟计算，不影响计算结果准确性且能节约计算资源，降低计算成本。

1.3 湍流模型选择

选择M3网格进行数值模拟计算，采用SSTk-ω模型、标准k-ω模型、标准k-ε模型、RNGk-ε模型和RSM模型分别在入口速度u=0.5、1、1.5、2 m/s对应工况进行数值模拟计算。为保证湍流流动充分发展，选取计算区间为z=0.25 m流动横截面与z=0.75 m流动横截面之间的流体压降Δp。图4示出不同湍流模型的摩擦阻力系数f与Blasius公式计算的理论值。

由图4可知，5种不同湍流模型对应的f与理论值在雷诺数较大时都具有较好吻合性。其中SSTk-ω模型和标准k-ω模型的f与理论值在雷诺数较小时相差较小，而标准k-ε模型、RNGk-ε模型以及RSM模型的f在雷诺数较小时则相差很大。SSTk-ω模型和标准k-ω模型之间，前者相比于后者在低雷诺数下的f更加接近于理论值，且其随雷诺数变化趋势更加接近于理论值变化趋势。在5种湍流模型中，SSTk-ω模型对于子通道湍流流动数值模拟最为合理精确，因此选择SSTk-ω模型作为本文数值模拟的湍流模型。

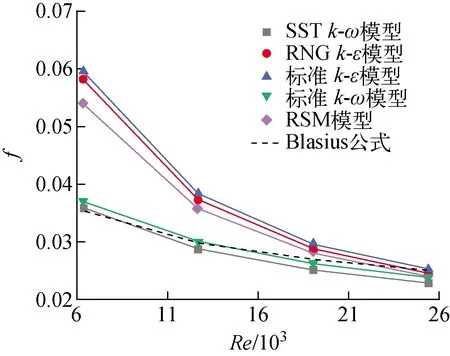
图4 不同湍流模型摩擦阻力系数与理论值

2 数值模拟结果分析

2.1 间隙湍流热流法

保持两个相邻子通道具有相同的几何形状和相等的入口质量流速。两个相邻子通道内流体保持一定入口温差，其中通道i中流体温度较高，通道j中流体温度较低。保证没有其他的热流输入，两个相邻子通道间的传热只能够通过热传导和湍流交混两个过程来实现。

由湍流交混和通过间隙传导而产生的热量(在稳态流动下)等于：

Qtotal=Qin-Qout=q″totalSijΔx

(1)

通过间隙的热流为：

(2)

其中：ρ为子通道中流体密度，kg/m3；U为子通道中流速，m/s；Aflow为子通道面积，m2；cp为比定压热容，J/(kg·K)；Sij为子通道之间的间隙，m；Δx为作用的长度，m；Qtotal为由湍流交混和通过间隙传导而产生的热量，kJ；Qin为流体进口热量，kJ；Qout为流体出口热量，kJ；q″total为通过间隙的总热流，kW；Tin为入口流体温度，K；Tout为出口流体温度，K；i、j为子通道。

湍流交混系数β定义为湍流所导致的热流和轴向热流的比值，即：

(3)

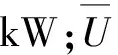
因为水的湍流导热率远大于其分子导热率，式(3)可改写为：

(4)

从理论上来讲，式(4)是将湍流和分子扩散的交混系数一并计算出来的，同时在这里应强调基于子通道热平衡的热流将包括对流和扩散传输的贡献。真正的差别只在于局部(近间隙)的热平衡。由此可得：

(5)

设置入口速度u=1.5 m/s，保持其他条件不变进行数值模拟，计算轴向z=0.05～0.75 m每间隔0.1 m处两子通道横截面温度，再采用间隙湍流热流法计算湍流交混系数轴向变化，如图5所示。

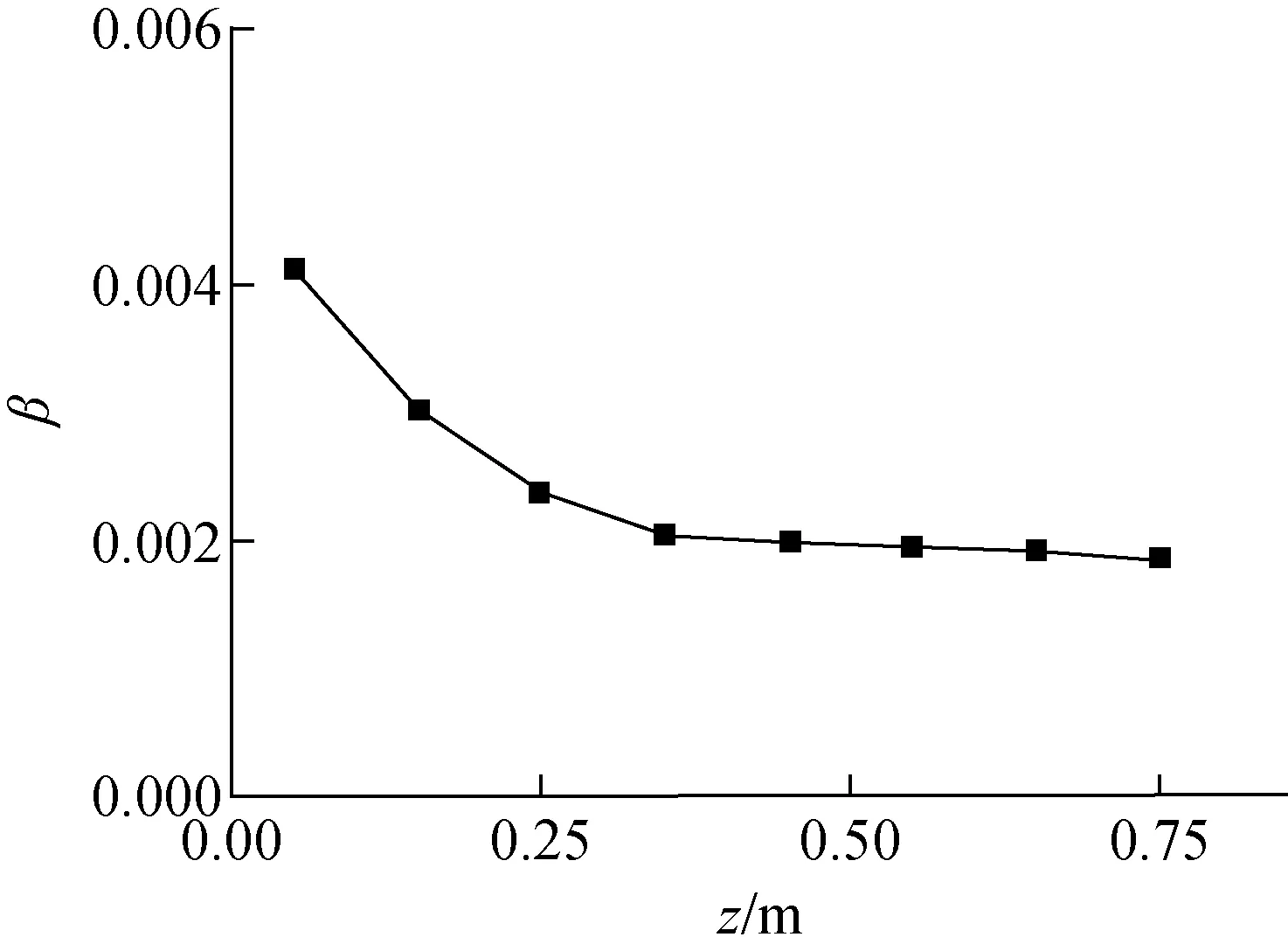
图5 间隙湍流热流法计算的湍流交混系数轴向变化

由于存在入口段效应，在轴向z=0.35 m前所算得的湍流交混系数较大且沿着轴向方向迅速减小。在轴向z=0.35 m后湍流交混系数趋于稳定近似等于2×10-3。将对应雷诺数Re以及动力黏度μ代入Galbraith计算关系式：

(6)

其中，W′ij为湍流交混率。

由单相湍流交混系数计算式可得：

(7)

对应单相湍流交混系数β计算结果为2.79×10-3，与间隙湍流热流法所得结果保持数量级10-3相吻合，且数值差异不大。因此，采用间隙湍流热流法能较准确地计算湍流交混系数，且沿流体轴向流动方向能反映局部湍流交混系数的变化。

2.2 类比浓度计算法

通过在子通道冷却剂中加入一定浓度示踪剂，再测定示踪剂浓度在子通道中轴向变化情况，从而推导计算湍流交混系数。通常将浓度沿轴向变化数据拟合如式(8)来确定湍流交混率W′ij：

(8)

其中：Gi和Ai分别为子通道i的质量流速和横截面积；Ci(z)为子通道i轴向z处的示踪剂浓度；Δz为两个轴向位置之间的距离。

由于传质方程与传热方程相类比，浓度沿轴向的变化来推算湍流交混率，可类比为温度沿轴向的变化来推算湍流交混率，从而通过轴向温度变化得到湍流交混率：

(9)

其中，Ti(z)为子通道i在轴向z处的流体温度。

本文以2005～2017年长江中游城市群31个地级市为研究对象，研究产业集聚、技术创新对经济增长的影响。专利申请量来源于各城市每年的国民经济和社会发展统计公报，消费价格指数来源于湖北、湖南、江西3省的统计年鉴，2005～2016年其余数据来源于2006～2017《中国城市统计年鉴》，2017年数据来源于各市2017年国民经济和社会发展统计公报。

设置入口速度u=1.5 m/s，保持其他条件不变，计算轴向z=0.05～0.75 m每间隔0.1 m处两子通道横截面温度，再采用类比浓度计算法计算湍流交混系数的轴向变化，如图6所示。

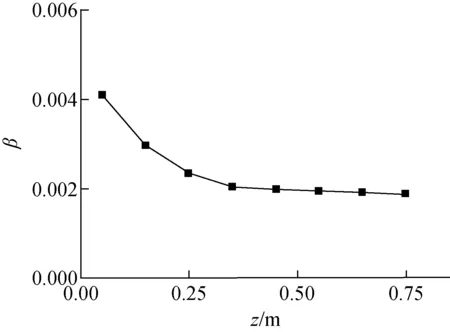
图6 类比浓度计算法得到的湍流交混系数轴向变化

类比浓度计算法所计算结果同样存在入口段效应，在轴向z=0.35 m前所算得湍流交混系数较大且沿着轴向方向迅速减小。在z=0.35 m后湍流交混系数趋于稳定近似等于2×10-3。湍流交混系数数量级在10-3，同样与Galbraith计算关系式计算结果相吻合，且在数值上差异不大。

2.3 两种计算方法比较

对比间隙湍流热流法与类比浓度计算法所得到的湍流交混系数轴向变化，可看出两者几乎一致，相对偏差不超过1.5%，并且两者具有相同的轴向变化趋势，能很好地体现出流体流动入口段效应，对于湍流交混系数计算具有较高精度。

2.4 单相湍流交混系数拟合关系式

本文在子通道水力直径、燃料棒直径以及间隙宽度都一定的情况下，对相邻两子通道湍流交混进行数值模拟，计算得到不同雷诺数下单相湍流交混系数。其他条件一定下，分析雷诺数对单相湍流交混系数的影响，并拟合雷诺数与单相湍流交混系数的关系式。雷诺数范围为4 500～34 000。

假设湍流交混系数与雷诺数关系式为幂指数关系：

β=bRea

(10)

其中，a、b为待定常数。

lgβ=lgb+algRe

(11)

对其进行拟合可得如图7所示的结果。

由图7可知，类比浓度计算法与间隙湍流热流法拟合直线斜率分别为a1=0.092 7、a2=0.091 5，与y轴截距分别为b1=-3.108 2、b2=-3.113 2，对应关系式中a1=0.092 7、a2=0.091 5，b1=0.000 78、b2=0.000 77，故单相湍流交混系数拟合关系式为：

图7 幂指数对数化拟合图

β1=0.000 78Re0.092 7

(12)

β2=0.000 77Re0.091 5

(13)

假设湍流交混系数与雷诺数关系式为多项式关系：

β=aRe2+bRe+c

(14)

对其进行拟合，结果如图8所示。

图8 多项式拟合曲线

由图8可知，拟合曲线a1=-1.377×10-12、a2=-1.309×10-12，b1=5.461×10-8、b2=5.209×10-8，c1=0.001 43、c2=0.001 41，故单相湍流交混相系数拟合关系式为：

β1=-1.377×10-12Re2+

5.461×10-8Re+0.001 43

(15)

β2=-1.309×10-12Re2+

5.209×10-8Re+0.001 41

(16)

上述幂指数、多项式拟合关系式都是通过最小二乘法进行曲线拟合，各类关系式对应相关系数R2列于表2。

表2 各类拟合曲线相关系数

在雷诺数小于15 000时，湍流交混系数随雷诺数的增大而增大，但增长幅度较小。而在雷诺数大于15 000时，随着雷诺数的变化湍流交混系数几乎不变。因此在经过充分发展后，可认为湍流交混系数β为一常数，拟合湍流交混系数常数如图9所示。

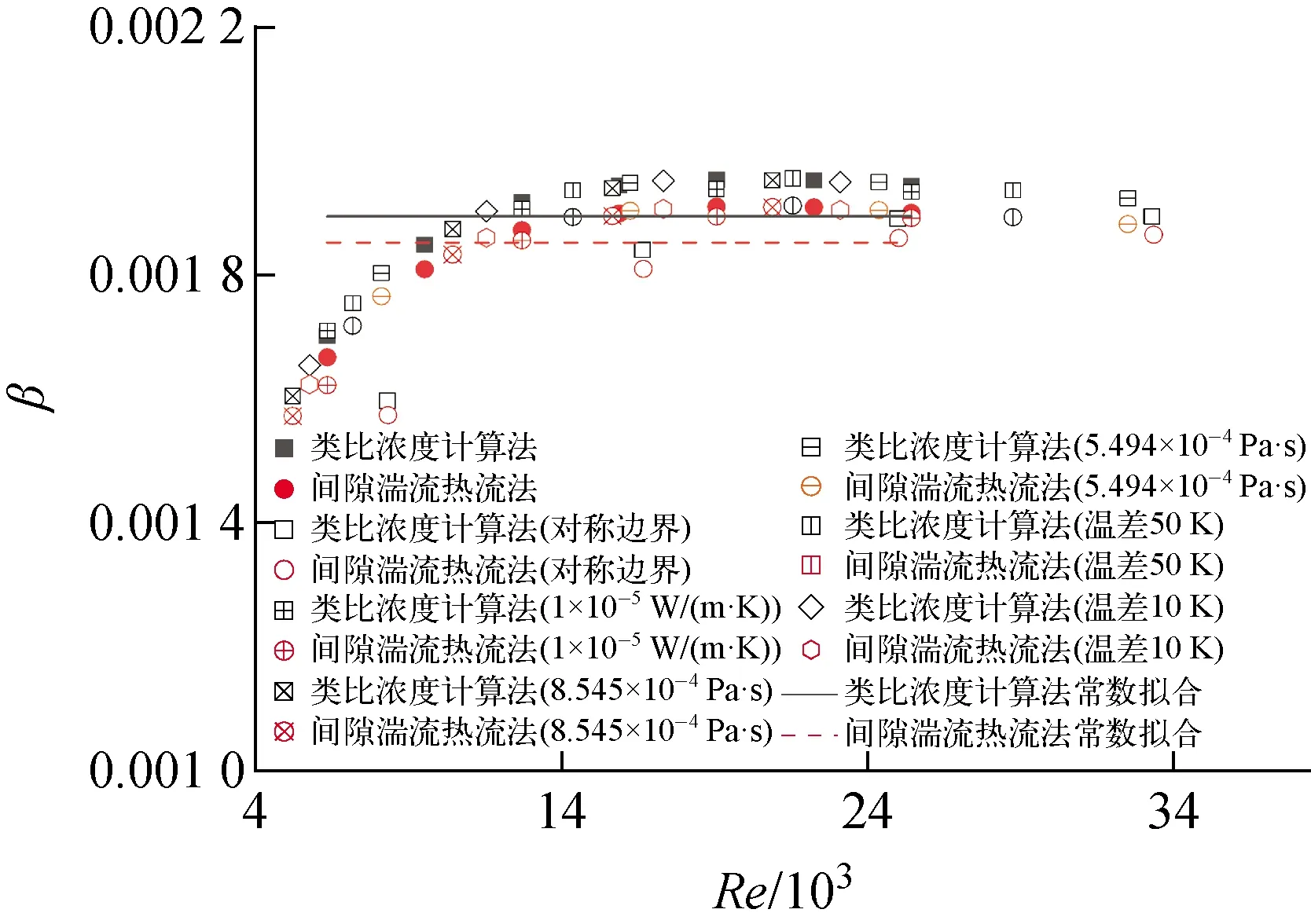
图9 湍流交混系数常数拟合图

由图9可知，拟合湍流交混系数β常数分别为β1=0.001 9、β2=0.001 85，在雷诺数小于15 000时β与拟合值相差最大近10%，而在雷诺数大于15 000时β与拟合值相差最大近3%，类比浓度计算法与间隙湍流热流法所对应拟合常数相差仅为2.6%。

综合上述几种拟合方式，多项式拟合虽相关系数R2较高，但由于多项式拟合关系式结构复杂且一次项与二次项系数太小，因而其拟合关系式不太适用较广范围。虽然幂指数拟合关系式相关系数R2不是最高，但其相关性能满足要求，且拟合单相湍流交混系数关系式结构简单以及系数大小合适，较为简单清晰便于广泛适用。

使用间隙湍流热流法计算湍流交混系数时忽略了分子导热，进而导致使用类比浓度计算法所得的湍流交混系数略大于间隙湍流热流法的结果。同时随着雷诺数增大，一方面湍流交混强度增强，另一方面间隙处涡旋的影响范围较小，因此由湍流引起的能量转移会减小，两方面的综合作用会使得湍流交混系数处于变化波动较小的状态。

但总的来说，采用类比浓度计算法与间隙湍流热流法能准确计算子通道湍流交混系数，两者计算湍流交混系数的轴向分布没有显著差异。

3 结论

本文使用CFD数值模拟的方法对单相工况下反应堆堆芯棒束子通道间湍流交混特性进行研究，研究发现：采用类比浓度计算法与间隙湍流热流法能够准确计算子通道湍流交混系数，两者计算湍流交混系数的轴向分布没有显著差异；同时发现湍流交混系数随雷诺数的增大而增大，但雷诺数足够大时保持基本不变。基于CFD计算结果拟合得到单相湍流交混系数的计算关系式。本文对于子通道间湍流交混效应的研究有一定的帮助。