基于MPS方法的离散固体与流体相互作用数值模拟研究
肖鑫坤,蔡庆航,陈荣华,*,丁 雯,张 魁,郭凯伦,田文喜,秋穗正,苏光辉
(1.西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049;2.西安交通大学 核科学与技术学院,陕西 西安 710049)
移动粒子半隐式(MPS)方法[1]已有近30年的历史,其主要思想是将流体用一系列离散的带有拉格朗日属性的粒子表示,将流体运动控制方程的各项微分算子通过粒子间相互作用来表达,以实现对流体运动的准确模拟。相较于网格方法,MPS方法不存在网格畸变这一固有缺陷,而其拉格朗日特性使得MPS方法在捕捉自由表面和界面运动、捕捉相态变化、固体变形等方面具有独特的优势,因此得到的了众多研究者的关注,并在核工程领域得到了广泛应用。
在核反应堆严重事故分析领域,通过在MPS方法中引入传热相变模型、黏度变化模型[2]和共晶反应模型,使用MPS方法对管内流动凝固[3-5]、沸水堆燃料支撑件内的熔融物流动凝固[6-7]、铅铋平板消熔[7]、共晶反应[8-9]、熔融物与混凝土相互作用[10-11]、燃料元件熔化[12-13]、锆水氧化反应[14]和ADS颗粒靶熔化[15]等核反应堆严重事故关键现象展开了模拟研究,这些研究验证了MPS方法在传热相变和物质变化中应用的可行性和准确性,大大拓宽了MPS方法的应用范围。
在核反应堆中发生堆芯熔化严重事故时,堆芯熔化后产生的熔融物发生迁徙,未发生熔化的燃料微粒、基体碎片、包壳碎片也被熔融物夹带着发生迁徙,这是一个包含大量离散固体的流固耦合问题。已有的严重事故程序对堆芯熔化问题进行研究时,大都采用集总参数的烛化模型,如MELCOR等,这种模型计算得到的结果较为粗糙,且不考虑未熔化的离散固体之间的相互作用。
本研究使用MPS方法对这种现象进行模拟,对熔融物夹带的固体之间的相互作用以及液相与固相之间的作用进行分析。现有的处理方法难以进行准确的模拟,需要进行相关模型的开发。
本文在基于MPS方法的核反应堆关键热工安全现象分析软件平台(PANDA)上进一步发展离散单元法(DEM)耦合模块(PANDA-DEM),在使用的流固耦合模型中引入多相黏性的处理方法提高稳定性和准确性,并通过滑坡算例对本模块使用的流固耦合模型的稳定性和准确性进行验证。
1 数值模型
使用MPS方法对液相进行描述,分析流体的运动;使用DEM对固相进行描述,计算固体粒子之间的相互作用力;液相和固相之间的相互作用力被归纳为黏性力和压力作用。
1.1 液相
使用MPS方法来对流体的运动进行模拟,控制方程包括连续性方程和动量守恒方程:
(1)
(2)
式中:ρ为密度;t为时间;u为速度向量;p为压力;μ为黏性系数;g为重力向量;f为表面张力。
流体的运动过程通过上述控制方程进行约束并得到,具体的思路是先显式计算动量守恒方程中的黏性项、重力项和表面张力项,得到估算的速度和位置,通过不可压缩流体的连续性方程建立压力泊松方程,使用求解得到的压力梯度对估算得到的粒子速度和位置进行修正。
1.2 固相
使用DEM[16]求解离散固体的整体运动状态。在DEM理论中,离散的结构单元被称为颗粒,具有与MPS方法中的粒子相似的性质。这两种方法都是将介质进行离散化处理,通过对离散单元的运动分析得到介质整体的运动状态,因此能够在同样的框架内进行计算。
DEM的主要思路是对每一个离散单元进行受力分析,通过牛顿第二定律得到其运动状态。
首先分析离散单元的运动方程,对于当前时刻,任意离散单元均可由牛顿第二定律得到两个加速度:
(3)
(4)
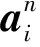
下一时刻离散单元的速度u和角速度ω、位移r和旋转角度θ为:
(5)
(6)
(7)
(8)
式中,ΔtDEM为DEM计算的时间步长。
由此可得到单个离散单元随时间的运动。离散单元加速度的合力与合力矩通过下式计算:
(9)
(10)
ΔTXe,j→i=krΔθX,i,j
(11)
Td,j→i=crΔθX,i,j/ΔtDEM
(12)
式中:e和d分别为弹性力和阻尼力;k和c分别为弹性系数和阻尼系数;下标n和s分别代表接触面的法向和切向,其中y轴方向和z轴方向同为切线方向,计算时只有方向不同,其余参数均相同;FX,j→i和FY(Z),j→i为离散单元j对离散单元i的法向作用力和切向作用力;ΔXi,j和ΔY(Z)i,j为离散单元j和离散单元i在坐标系x、y、z3轴方向上的相对位移;ΔTXe,j→i为x轴方向的回转力矩的弹性增量;ΔθX,i,j为离散单元j与离散单元i的相对转角;Td,j→i为离散单元j与离散单元i之间回转力矩的阻尼分量;下标r表示回转。需要指出的是,计算固体之间的相互作用力时需要使用的相对位移通过速度和时间步长得到,而两个固体粒子之间的相对位置通过上一个时间步长的位置得到。
1.3 流固耦合
通过将DEM计算离散固体之间的相互作用力视为MPS方法的一个模型来进行二者之间的耦合,也就是在PANDA中开发DEM耦合模块PANDA-DEM。将DEM的离散单元视为MPS方法中的粒子,二者使用相同的粒子直径和作用半径。对于离散固体体系受到的外力,也就是流体对固体的作用力,通过式(13)[17]进行计算:
(13)
式中:下标ls表示流固耦合界面;f为界面上的力。
式(13)认为,流体对固体的作用力主要是流体对固体的压力作用和流体对固体的黏性力作用,当然需要认识到这样的作用只发生在流体与固体接触的部分,也就是固体粒子之间的相互作用只需要进行DEM计算,只对与流体粒子发生接触的那部分固体粒子进行MPS方法中的黏性项和压力项计算。
此时,固体粒子对流体粒子的作用也就是流体粒子与固体粒子之间的耦合作用力fls的反向作用力,会被包含在流体粒子受到的黏性力和压力中,因为流体粒子的这两个力是通过作用域内全部粒子对它的作用力的积分得到,包括固体粒子。对于固体粒子而言,需要针对不同的情况进行分析。对于存在于流固相界面上的固体粒子,其控制方程为:
(14)
对于不在相界面上的固体粒子:
(15)
式中:fDEM为使用DEM方法计算得到的固体粒子之间的相互作用力;ρs和ρl为固体的密度和流体的密度;ρsg为固体粒子受到的重力,对于fDEM而言,它是通过DEM模型计算得到的由于固体之间的相互作用产生的力,这个力通过两个时层之间粒子的相对位移来计算得到。
在计算流体粒子与固体粒子之间的耦合作用力中的黏性项时,为充分考虑固体粒子与流体粒子之间存在的物性差异,体现固体粒子的物理性质,也为了避免在流体与固体之间产生一个尖锐的相界面,通过引入多相流的处理思路,给予离散的固体一个与其物理性质相关的黏性系数,并通过调和黏性系数来计算黏性项:
(16)
式中,μij为调和黏性系数,不难看出μij在μi和μj相等时退回单相,而两个黏性系数不同只在相界面上出现,这是一个广义模型。
此时黏性项采用式(17)进行计算:
G(‖rj-ri‖,re)
(17)
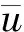
通过计算发生接触的流体粒子与固体粒子之间的黏性力与压力作用,将这两个力作为DEM计算时的外部输入,就能得到离散的固体在流体作用下的运动,也就实现了对流体与固体之间相互作用的耦合分析。
一般情况下,MPS方法计算的时间步长要大于DEM计算,时间步长的耦合通过先对流体粒子推进一个MPS方法的时间步长,如果存在DEM计算,就进入DEM计算内循环,推进数个DEM时间步长,令其总的时间步长等于MPS方法计算时间步长来实现。
PANDA-DEM的算法流程如下:1)建立研究对象的初始状态模型,输入初始参数;2)初始化速度和位置参数,用于后续的计算;3)推进1个时间步长,使用MPS方法计算粒子的速度和位置;4)判断是否发生固体粒子之间的相互碰撞,如果发生,进入DEM计算内循环,如果不发生,结束当前时间步长,进入下一时间步长;5)进入DEM内循环后,使用DEM模型计算固体粒子的速度和位置;6)结束内循环,进入下一时间步长。
2 滑坡算例的模拟
通过两个滑坡算例对模型的稳定性与准确性进行分析:算例1是固体滑坡算例,即纯离散固体颗粒沿滑坡的下落过程,能够验证耦合分析模型对于固体运动的计算能力;算例2是水下滑坡算例,即离散的固体颗粒沿斜坡下落的过程中与流体发生耦合,流体流场与固体运动都会受到流固耦合作用的影响。
2.1 固体滑坡算例
固体滑坡算例是干颗粒材料(即玻璃微珠)沿45°光滑斜面的滑动,图1示出计算域的初始粒子排列。在实验开始时,将挡板快速移出,颗粒状材料受到重力的作用沿滑坡向下滑动。固体滑坡算例基于Tajnesaie等[19]的实验设计得到,需要使用的几何参数为:h1=0.2 m,h2=0.14 m,α=45°。DEM计算需要使用的参数为:法向弹性系数kE=2×105N/m,法向阻尼系数cE=30 N/m,切向弹性系数kN=2×104N/m,切向阻尼系数cN=10 N/m,回转弹性系数kR=800 N/m,回转阻尼系数cR=10 N/m,最大静摩擦因子μ=0.08,时间步长=10-7s。此算例的目的是评估改进模型处理固相行为的能力,实验中使用的玻璃珠密度为2 650 kg/m3。本实验中使用的粒径为0.001 m,粒径与实验所使用的玻璃微珠直径保持一致,最终算例使用的粒子总数为4 108,算例是二维的实验1∶1建模,粒子数量由实验参数确定,这里不考虑粒子数量对模拟结果的影响。算例计算使用的时间步长均在符合Courant-Friedrichs-Lewy条件的前提下,考虑计算资源的限制得到。由于玻璃微珠不是流体,黏性系数无法直接得到,本文中所使用的数值0.08是参考摩擦系数得到的。

图1 算例1计算域初始粒子排布
图2示出算例1模拟结果,包括粒子配置,并与对应的无量纲时间点的实验快照进行了比较,无量纲时间T通过下式计算。
(18)
式中:t为真实时间;h0为固体滑坡在t=0时底端和顶端的距离。
由图2可见,实验与数值模拟结果显示出相似的特征,总体符合得较好。对于图2a中存在的模拟结果与实验结果符合不是太好的问题,是由于实验开始时,挡板并不是瞬时移出,滑坡会受到挡板的干扰。对于图2b中出现的模拟粒子积分面积小于实验颗粒面积的情况,是因为实验是三维的,固体滑坡在拍摄方向上的剖视图面积不均匀,而拍摄得到的面积必然会大于平均面积,也就显得积分面积大于二维模拟结果的积分面积。颗粒材料的运动也通过绘制滑坡前沿无量纲滑动的长度来量化和验证,如图3所示,实验测得的滑坡前沿无量纲滑动长度与模拟得到的结果进行对比,移动前沿的相对误差在固体颗粒运动稳定后,最大不超过5.5%。

图2 算例1模拟结果与实验结果的对比

图3 算例1滑坡前沿无量纲滑动的长度对比
2.2 水下滑坡算例
算例2计算域初始粒子设置如图4所示,这是一个水下滑坡的三维模型,在移除挡板后玻璃粉末开始运动。算例2的几何参数为:z=0.12 m,h1=0.4 m,h2=0.334 m,h3=0.32 m,α=35°。DEM计算中需要使用的参数为:kE=105N/m,cE=50 N/m,kN=104N/m,cN=10 N/m,kR=800 N/m,cR=10 N/m,μ=0.08,时间步长=10-5s。算例2基于文献[20]中浸没在水中的颗粒材料(玻璃粉末)沿35°光滑斜面滑动实验设计,算例2能评估模型在模拟大量离散固体流固耦合问题的能力。

图4 算例2计算域初始粒子排布
将所建立的流固耦合模型和初始模型数值模拟结果与文献[19]中的实验结果进行比较,如图5所示。实验结果用高速摄影机记录,记录时刻为0.02、0.17、0.32和0.47 s。在0.17 s时,流体表面的结构与计算结果相似。随着玻璃粉末组成的滑坡开始下降,流体表面出现凹陷,这在计算结果中也可清楚地观察到。在0.32 s时,由于反弹,流体表面出现两组波浪,这一现象在模拟计算结果中也得到了清晰的反映。在0.47 s时,剖面图显示此剖面上滑坡并不连续,但整个三维的滑坡是连续的,即在z方向的其他位置是连续的,这是由于MPS方法模拟的固体粒子尺寸与实际玻璃粉末尺寸相比较大,使得固体粒子数相对较少,随着滑坡的进行,部分位置就会出现这种情况,是合理的。由图5可见,滑坡形状在各时间点与实验结果对应得较好,数值模拟结果与实验结果吻合较好,表明该模型具有分析流固耦合问题的能力。
根据滑坡移动前沿在斜坡上相对于初始前沿点的移动距离,定量分析了滑坡前缘的位置,结果如图6所示,模拟结果与实验结果吻合较好。在初始阶段,由于挡板的移出对实验结果影响较大,距离变化较小,相对误差较大,不具有参考价值。运动稳定后最大相对误差仅为8.6%,证明了模型的准确性。
3 结论
本文在基于MPS方法的核反应堆关键热工安全现象分析软件平台(PANDA)上开发了适用于分析流固耦合问题的PANDA-DEM模块,并通过引入多相流的思路来处理相界面上的黏性来提高所使用模型的稳定性和准确性。对固体滑坡和水下滑坡算例进行了数值模拟,并与实验结果进行对比。通过定性对比固相的整体运动和液相流场,定量比较滑坡前沿的移动距离,对模型进行了验证,结果表明:1)本研究将离散单元法引入MPS方法框架内构建的DEM模型可用于模拟固体颗粒滑坡行为,滑坡前沿无量纲移动长度实验和模拟的相对误差不超过6.3%;2)本研究中基于DEM模型和MPS方法构建的流固耦合方法可用于模拟水下固体滑坡行为,滑坡前沿移动距离实验和模拟的相对误差不超过8.6%。因此,本研究中建立的模型可对包含大量离散固体流固耦合问题进行准确分析,后续工作会将此模型扩展到对核反应堆堆芯熔化严重事故的分析模拟中。

