发动机小直径管X 射线底片数字化图像增强技术
王克广 ,岳 乔 ,缪 伟 ,邬冠华
(1.中国航发动力股份有限公司,西安 710000;2.南昌航空大学 测试与光电工程学院,南昌 330063)
0 引言
传统的X 射线胶片成像技术由于发展时间长、相关检测标准体系较完善、成像质量高等特点,依然是许多工业射线检测的主流手段。但胶片具有长时间存放困难、底片破损、不利于管理等难题。通过扫描技术将胶片转存为数字图像,是解决这个问题的有效手段。然而,由于扫描中会不可避免地产生对比度不足、分辨率降低等图像退化现象,因此,需要对扫描的数字图像进行适当增强。
由于经扫描转存的是灰度图像,对该图像的增强方法应用较为广泛的主要有基于直方图均衡[1](Histogram Equlization,HE)和基于Retinex 理论[2]的方法。直方图均衡主要是通过重新映射灰度分布,改变图像的直方图均匀程度,使得图像全局增强[3]。自适应对比度直方图增强[4-5](Adaptive Histogram Equlization,AHE)是将图像分成尺寸相同的数张局部图像,分别映射每张局部图像的直方图,可以有效增强图像局部细节,但会放大边缘噪声;限制对比度的自适应直方图均衡[6-7](Contrast Limited Adaptive Histogram Equalization,CLAHE)算法通过限制每个局部图像的直方图分布水平,可以有效控制图像的噪声水平,但容易出现局部色彩失真的现象。以高斯滤波器为环绕函数的MSR 算法[8-12],图像增强效果明显,细节更加丰富。
以上2 种算法的图像增强效果都较为依赖算法的参数调节。如CLAHE 易受直方图灰度频数截断阈值影响,截断阈值大,图像增强效果弱;反之,增强效果强,但噪声也会随之放大。MSR 算法主要可调参数为中心环绕因子,不同场景的图像中,低中高3 个尺度所对应的中心环绕因子取值完全依靠经验。因此,如何寻找合适的参数对提升算法性能至关重要。
近年来,将智群算法和图像增强方法相结合的自适应增强算法成为研究热点。文献[13]使用灰狼寻优算法结合模糊集增强实现改善图像;文献[14]使用粒子群自适应优化伽马校正参数,融合多个权重评价函数作为粒子的适应度目标值以增强图像细节等;文献[15]提出的麻雀搜索算法(Sparrow Search Algorithm,SSA)是近来较为优秀的智群算法,具有搜索精度更高,迭代速度更快,具有更好的鲁棒性等特点,有利于寻找最优参数。
本研究通过采用麻雀搜索算法,结合改进MSR 图像增强方法,以双边滤波器函数替代原高斯滤波器中心环绕函数,以图像空域、频域及信息熵线性处理作为SSA 种群适应目标,通过寻找MSR 最优中心环绕因子,实现图像自适应增强。
1 MSR 算法及SSA 搜索算法
1.1 MSR 算法
MSR 是以高斯滤波器作为中心环绕函数的算法,在高中低3 个尺度调节中心环绕因子,以实现图像动态范围压缩、边缘对比度提高,其算法可表示为:

式中:N表示尺度个数;n=1,2,…,N;ωn为单个尺度权重,满足为不同尺度因子下的高斯中心环绕函数,其数学表达式为:

式中:(x,y)为像素点的坐标;K为图像色彩通道数,对只含单个通道的灰度图像来说,K=1;σn为不同尺度的环绕因子,根据经验常见的低中高3 个尺度分别取值15、80、120。
1.2 SSA 搜索算法
SSA 是一种新型的群智能优化算法,主要是受麻雀的觅食行为和反捕食行为的启发。假设一个N维空间存在D只麻雀,种群可以表示为X=[xi1,xi2,…,xin,…,xiN],其中,i表示麻雀个体序号,xin表示第i只麻雀在第n维的位置。所有麻雀的适应度可以表示为F(X)=[f(xi1,xi2,…,xin,…,xiN)],其中,f表示适应度函数值。在每次迭代中,设置一定比例的发现者,通常占种群的80%~90%,发现者位置更新公式为:

式中:t表示种群当前迭代次数;α为(0,1]之间随机生成数(保留1 位小数);T表示种群最大迭代次数;H是服从标准正态分布的随机数(保留1 位小数);M表示大小为1×n的全1 矩阵;EW、S分别表示预警值和安全值,取值范围为EW∈[0,1],S∈[0.5,1],保留1 位小数。当EW<S时,种群所处环境安全,发现者扩大搜索范围,引导种群获取更高的适应度值;当EW≥S时,表明种群中有麻雀察觉到危险,发出信号示意同伴,同时飞离危险区域。对于剩下的加入者,位置更新公式为:

式中:xw表示麻雀处于最劣位置,远离食物;xb表示麻雀处于最优位置,非常靠近食物;当i>D/2 时,表明第i个加入者没有获取食物,需要继续跟随发现者以寻找食物。
根据麻雀觅食的习性,设计侦察预警机制,在种群中随机生成10%~20%的麻雀意识到危险,位置更新为:

式中:f表示麻雀的适应度值,fb和fw分别为当前种群最优适应度值和最差适应度值;当fi>fb时,表明此麻雀正处于种群的边缘,其安全受到严重威胁;β为随机生成的步长控制参数,服从均值为0,方差为1 的正态分布;当fi=fb时,表明该麻雀正处于种群中间,意识到危险的存在,需要改变飞行方向远离危险;K也表示步长控制参数,是一个取值范围[-1,1]的随机整数,表示麻雀移动的方向。为避免分母为0 的情况出现,加上一个极小常数e。
2 MSR 算法改进及参数寻优
MSR 算法主要是利用高斯中心环绕函数的σn取值不同,其保留边缘和滤除噪声能力不同的特性,达到提高图像增强能力。但高斯中心环绕函数属于线性平滑滤波器,有较好的消除噪声能力,但保留边缘能力较弱,增强后的图像容易出现细节丢失、边缘弱化等问题。
本研究使用边缘保留能力更强的双边滤波函数替换原高斯中心环绕函数,达到保留边缘、去除噪声的目的。双边滤波属于非线性滤波器,考虑了像素的欧式距离、像素范围域的差异,具有更强的保边、降噪、平滑能力。
2.1 改进MSR 算法的双边滤波函数
双边滤波函数数学表达式为:
式中:f(k,l)为滤波窗口待处理图像的中心像素;f(x,y) 为滤波窗口待处理图像的其他像素;σd为空域中心环绕尺度因子;σr为值域中心环绕尺度因子;||*||2表示2 范数,也就是2 个点像素差值的绝对值的平方;w(x,y,k,l)为双边滤波函数;T(x,y)是滤波之后的像素值。
双边滤波核可以看作空域滤波核与值域滤波核的乘积:

式中:wd表示空域滤波核,ws表示值域滤波核。以滤波窗口大小为100×100,σd=40,σr=10 为例,空域滤波核、值域滤波核及双边滤波核示意图如图1所示。

图1 滤波核示意图Fig.1 Schematic diagram of filter core
为测试双边滤波保留边缘和去除噪声特性,绘出像素尺寸100×100 的灰度图像,分为大小相同的左右两部分,左边部分像素值均为10,右边部分矩阵像素均为120,用于模拟图像中的灰度剧烈变化(图2a)。对整幅图像添加方差为0.13、标准差为10 的高斯噪声(图2b)。使用高斯滤波器和双边滤波器对叠加了噪声的图2c 进行滤波,边缘灰度变化如图3 所示。

图2 灰度变化模拟图像Fig.2 Simulated image of gray change
从图3a 可以看出,图像高频信息和低频信息之间垂直过度,变化剧烈,表明边界尖锐清晰,但高频和低频两部分幅值起伏较大,噪点较多;经过高斯滤波后,高频和低频信息幅值变化较为均匀,噪点被抑制,但边缘垂直过度变为斜坡过度,此时边缘被模糊(图3b);经过双边滤波之后,高频和低频噪点被抑制的同时保留了原边界的垂直过度特性,具有良好的降噪和边缘保持能力(图3c)。多尺度高斯中心环绕函数的表达式为:

图3 滤波灰度变化Fig.3 Boundary under different filtered

式中:K为图像色彩通道数,对灰度图像K取1;σdn和σrn分别为相同尺度下的空域和值域环绕因子,n取值1、2、3,分别表示低中高3 个尺度。中心环绕函数变为2 个参数3 个尺度可调,并且不同图像所需要的σdn和σrn值不同,因此,需要利用搜索优化算法找到这2 个参数的最优值组合。
2.2 适应度函数
SSA 算法故需要设计一个基于图像质量评价的适应度函数,作为麻雀种群的优化目标函数。选取图像梯度、频域及图像熵3 个指标作为联合评价指标。
图像梯度是指图像某像素在x、y方向上的变化率(与相邻像素比较),是一个二维向量,采用Sobel 算子提取像素点水平方向和垂直方向的梯度值表达式为:

其中,⊗为卷积符号,gx、gy为Sobel 算子横向及纵向模板。

频域特性也可能反映图像信息,低频信息表示图像的基本灰度等级,高频信息表示图像的边缘和细节。基于图像二维离散傅里叶变换为:

图像熵(Entry)反映了一幅图像的细节信息丰富度,细节越丰富,其值越大,数学表达式为:
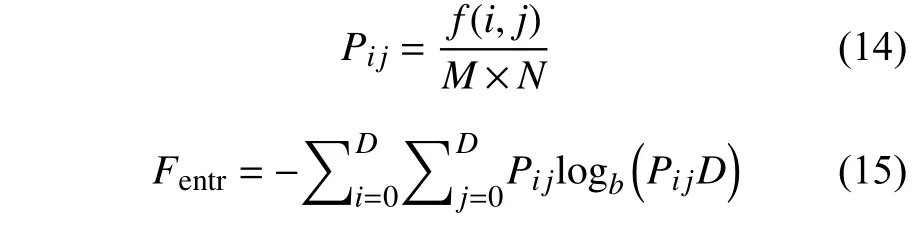
式中,M×N计算图像像素总数,f(i,j)表示像素,Pij表示像素出现的频率,b一般取值为2,D表示图像像素最大值。
分别计算图像增强前后,上述Fgrad、Ffreq、Fentr值按式(16)进行规一化处理。

其中,Fa,Fb分别是图像增强前后的评价指标。最后按各分量权重为1/3 作为适应度函数,即:

2.3 基于SSA 寻优增强算法流程
通过SSA 算法优化MSR 算法双边滤波的中心环绕因子,执行流程和伪代码如图4 所示。

图4 SSA 寻优增强算法Fig.4 Optimization enhancement algorithm of SSA
考虑到算法时效性和收敛性,设置种群规模D=40,最大迭代次数设置50,发现者数量设置为8,占种群总数的20%;加入者数量设置32,占种群总数的80%。同时,从种群中随机抽取20%的麻雀作为初始警戒者(这20%的麻雀具有双重身份,是警戒者的同时也有可能是发现者或加入者)。设置尺度n=3,σdn、σrn对应的取值上、下限分别为hdn、lrn,低尺度中心环绕因子上、下限分别为图像较短边长尺寸的5%、10%;中尺度中心环绕因子上、下限分别为图像较短边长尺寸的15%、25%;高尺度中心环绕因子上下限分别为图像较短边长尺寸的30%、40%。
3 算法结果分析
用前述算法对测试图像和底片扫描图像进行增强。考核不同滤波器、适应度函数、优化算法对图像增强质量的影响,以峰值信噪比(Peak Signal-to-Noise Ratio,PSNR),结构相似性(Structural Similarity,SSIM)、均方误差(Mean Squared Error,MSE)和Entry 等4 类客观指标进行量化评价。
3.1 测试图像
测试图像采用Lenna、kid 和tyre 等3 种常见标准图像。
1)不同滤波器。
在SSA 寻优增强算法框架下,将MSR 算法中心环绕函数分别替换为均值滤波器、中值滤波器、双边滤波器,对Lenna 图像添加方差为0.001、标准差为0.01 的高斯噪声,各滤波器增强结果如图5 所示。由图5 可见,3 种滤波器均能较好地滤除噪声,但保留边缘能力有所不同。均值滤波器模糊了边缘,细节表现较差(图5b);中值滤波在整体上加强了边缘,相比均值滤波有所提升,但在头发细节和帽子上细节保留较弱(图5c);双边滤波能保留更多的细节和边缘,头发和帽子边缘分辨更明显,视觉效果最好(图5d)。客观评价指标如表1 所示,在4 类评价指标中,双边滤波器取得最优值。

表1 不同滤波器下Lenna 图像客观评价指标Table 1 Objective evaluation index of Lenna image under different filters

图5 不同滤波器增强结果Fig.5 Enhancement results of different filters
2)不同优化算法测试。
为验证所选麻雀优化算法的有效性,与常见智群优化算法萤火虫优化、灰狼优化2 类算法进行对比,改进MSR 算法中心环绕函数均使用双边滤波器,适应度函数为联合评价函数。以kid 为测试对象,不同优化算法增强结果如图6 所示。
从图6 可以看出,3 类算法均都能有效提高图像对比度。萤火虫算法倾向于加强图像边缘,提高图像质量;灰狼优化算法倾向于将图像对比度加深;麻雀优化算法对图像整体增亮,线条过度更为柔和。对图像背景和小孩衣服标志局部放大可以看出,相比其他2 种寻优算法,经过麻雀优化算法寻优后局部细节更容易分辨,线条更加清晰。

图6 不同优化算法增强结果Fig.6 Enhancement results of different optimization algorithms
增强客观评价结果如表2 所示。在4 类评价指标中,麻雀优化算法增强在PSNR、Entry 取得最优值,SSIM 值与萤火虫算法结果相差不大。

表2 不同优化算法下 kid 图像客观评价指标Table 2 Objective evaluation index of kid image under different optimization algorithms
3)不同适应度函数测试。
为验证fitness作为目标适应度函数有效性,将Fgrad、Ffreq、Fentr分别作为适应度函数,以tyre为测试对象,增强结果如图7 所示。
图7a 倾向于产生强边缘,导致图像整体过度增强;图7b 频域强调高频信息导致边缘更为柔和,放大图像可以看出较暗部分线条增强有限,不易区分;图7c 图像整体偏亮,较暗区域得到增强,但整体图像失真;图7d 整体亮度较为适中,边缘清晰,局部放大能够识别螺栓,主观增强效果最好。增强客观评价结果如表3 所示。从客观评价结果可以看出,fitness作为适应度函数,整体表现最优。

表3 不同适应度函数下tyre 图像客观评价指标Table 3 Objective evaluation index of tyre image under different fitness function

图7 不同适应度函数增强结果Fig.7 Enhancement results of different fitness functions
3.2 底片扫描图像增强
图8、图9 为实际扫描的2 种类型胶片图像。图8a、图9a 为发动机小径管底片扫描原图及局部放大图,含气孔和夹渣缺陷,像素尺寸为2720×2040。2 张小径管原图对比度较低,整体有蒙雾感,细小缺陷隐藏在背景当中不易发现,图9a的背景区域更大,目标区域在整张图像中占比更小。
图8b 是使用CLAHE 方法增强后的图像,相比原图局部缺陷更加突出,但增强效果仍然较为有限,直径较小的缺陷难以观察;图8c 是使用MSR 方法增强后的图像,图像整体对比度确有提升,但偏暗且背景颜色不均匀,导致局部颜色加深,细小缺陷被隐藏;图8d 是使用本研究的增强方法,设置种群规模D=40,最大迭代次数设置50,发现者数量设置为8,加入者数量设置32,随机抽取20%的麻雀作为初始警戒者。σdn、σrn低中高3 个尺寸上、下限分别为102~204、306~108、714~816,进行优化参数图像增强。可以看出,整体原图视觉效果比较柔和,且对于细小缺陷加强效果明显,边缘更清晰锐利。

图8 第1 类航空小径管Fig.8 Aviation small diameter pipe of class 1
对于背景区域更大的第2 类航空小径管,图9b是使用CLAHE 方法增强后,背景出现大面积噪声,造成这一现象的原因是在底片扫描成像时受设备噪声影响,而CLAHE 增强算法并未加入任何滤波器,在增强过程中很容易放大这种噪声;使用MSR 增强后的图像(图9c)和图8c 情况类似,背景区域不均匀,局部颜色加深,不利于细小缺陷观察;文中增强算法的图像有效增强了细小缺陷和一些边缘(图9d)。

图9 第2 类航空小径管Fig.9 Aviation small diameter pipe of class 2
分别列出2 类图像适应度函数值,结果如表4所示。
从表4 结果可以看出,以适应度函数来分析,原图经过增强算法后,各项指标均有所增加,图像表现为整体对比度增加,边缘清楚,MSR 相较于CLAHE 有明显提升。本研究提出的算法与MSR算法从适应度函数指标上来说变化不大,这是因为双边滤波器本身也具有平滑噪声功能,图像中灰度边缘变化剧烈对计算结果值影响有限。
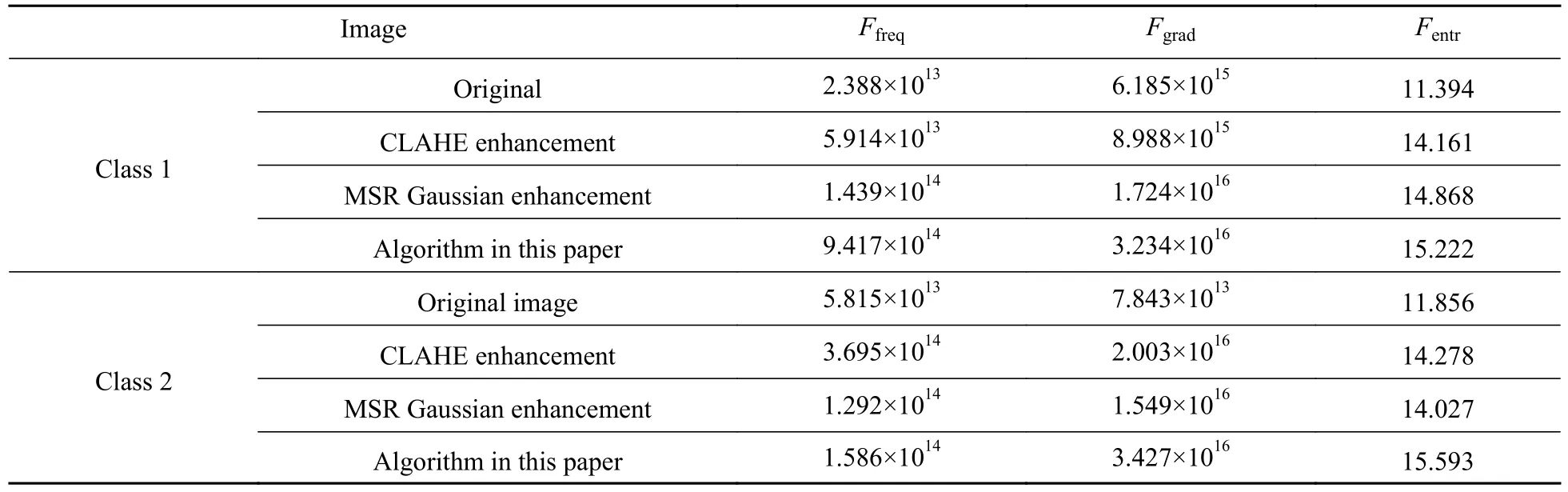
表4 2 类图像适应度函数值Table 4 Fitness function values of two classes of images
4 结论
1)使用双边滤波器改进传统MSR 算法,以麻雀搜索算法找到适应度函数下的最佳输入参数实现了图像增强。
2)在Lenna 等常用测试图像上采用本研究算法,以PSNR、SSIM、MSE、Entry 等4 类客观指标进行量化评价。结果表明:与均值滤波和中值滤波器相比,MSE 降低了31%;与萤火虫优化和灰狼优化算法相比,PSNR 提高了12%;与单一适应度函数相比,Entry 提高了25%。主观视觉上缺陷显示更加明显。
3)在2 类典型的航空发动机小径管底片扫描图像上,采用本研究算法与CLAHE 和传统MSR相比,图像梯度、图像频率特性和图像熵等客观指标最少提高了10%,图像主观视觉细节明显增强,边缘更加清晰。

