SINGULAR CONTROL OF STOCHASTIC VOLTERRA INTEGRAL EQUATIONS*
Nacira AGRAM Saloua LABED Bernt ØKSENDAL† Samia YAKHLEF
1.Department of Mathematics,KTH Royal Institute of Technology 10044,Stockholm,Sweden
2.University Mohamed Khider of Biskra,Algeria
3.Department of Mathematics,University of Oslo,PO Box 1053 Blindern,N–0316 Oslo,Norway
E-mail:nacira@kth.se;s.labed@univ-biskra.dz;oksendal@math.uio.no;s.yakhlef@univ-biskra.dz
Abstract This paper deals with optimal combined singular and regular controls for stochastic Volterra integral equations,where the solution Xu,ξ(t)=X (t) is given by Here dB (s) denotes the Brownian motion It type differential,ξ denotes the singular control (singular in time t with respect to Lebesgue measure) and u denotes the regular control (absolutely continuous with respect to Lebesgue measure).Such systems may for example be used to model harvesting of populations with memory,where X (t) represents the population density at time t,and the singular control process ξ represents the harvesting effort rate.The total income from the harvesting is represented by for the given functions f0,f1 and g,where T>0 is a constant denoting the terminal time of the harvesting.Note that it is important to allow the controls to be singular,because in some cases the optimal controls are of this type. Using Hida-Malliavin calculus,we prove sufficient conditions and necessary conditions of optimality of controls.As a consequence,we obtain a new type of backward stochastic Volterra integral equations with singular drift.Finally,to illustrate our results,we apply them to discuss optimal harvesting problems with possibly density dependent prices.
Key words Stochastic maximum principle;stochastic Volterra integral equation;singular control;backward stochastic Volterra integral equation;Hida-Malliavin calculus
1 Introduction
As a motivating example,consider the population of a certain type of fish in a lake,where the densityX(t) at timetcan be modelled as the solution of the following stochastic Volterra integral equation (SVIE):
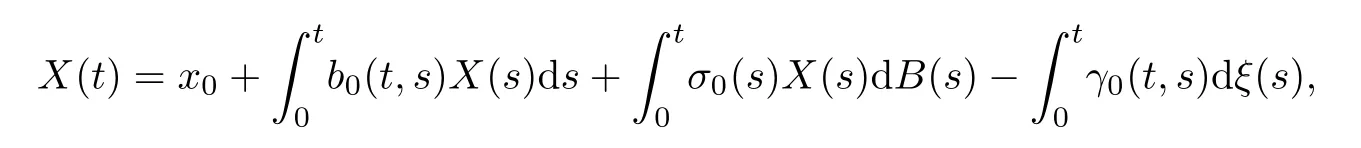
where the coefficientsb0,σ0andγ0are bounded deterministic functions,andB(t)={B(t,ω)}t≥0,ω∈Ωis a Brownian motion defined on a complete probability space (Ω,F,P).We associate to this space a natural filtration F={Ft}t≥0generated byB(t),assumed to satisfy the usual conditions.The processξ(t) is our control process.It is an Fadapted,nondecreasing left-continuous process representing the harvesting effort.It is called singular because,as a function of timet,it may be singular with respect to Lebesgue measure.The constantγ0>0 is the harvesting efficiency coefficient.It turns out that in some cases,the optimal processξ(t) can be represented as the local time of the solutionX(t) at some threshold curve.In this case,ξ(t) is increasing only on a set of Lebesgue measure 0.
Volterra equations are commonly used in population growth models,especially when age dependence plays a role.See,for example,Gripenberg et al[7].Moreover,they are important examples of equations with memory.
We assume that the total expected utility from the harvesting is represented by

where E denotes the expectation with respect toP.The problem is then to maximiseJ(ξ) over all admissible singular controlsξ.We will return to this example in Section 4.
Control problems for singular Volterra integral equations were studied by Lin and Yong[12]in the deterministic case.In this paper,we study singular control of SVIEs and we present a different approach based on a stochastic version of the Pontryagin maximum principle.
Stochastic control for Volterra integral equations was studied by Yong[14]and subsequently by Agram el al.[3,5]who used the white noise calculus to obtain both sufficient and necessary conditions of optimality.In the latter,smoothness of coefficients is required.
The adjoint processes of our maximum principle satisfy a backward stochastic integral equation of Volterra type and with a singular term coming from the control.In our example,one may consider the optimal singular term as the local time of the state process that is keeping it above/below a certain threshold curve.Hence in some cases we can associate this type of equations with reflected backward stochastic Volterra integral equations.
Partial result for existence and uniqueness of backward stochastic Volterra integral equation (BSVIE) in a continuous case can be found in Yong[14,15],and for a discontinuous case,we refer for example to Agram el al.[2,4]where there are also some applications.
The paper is organised as follows:in the next section,we give some preliminaries about the generalised Malliavin calculus,called Hida-Malliavin calculus,in the white noise space of Hida of stochastic distributions.Section 3 is addressed to the study of the stochastic maximum principle where both sufficient and necessary conditions of optimality are proved.Finally,in Section 4 we apply the results obtained in Section 3 to discuss optimal harvesting problems with possibly density dependent prices.
2 Hida-Malliavin Calculus
Let G={Gt}t≥0be a sub filtration of F,in the sense that Gt⊆Ft,for allt≥0.The given setU⊂R is assumed to be convex.The set of admissible controls,that is,the strategies available to the controller,is given by a subset A of the c`adl`ag,U-valued and G-adapted processes.Let K be the set of all G-adapted processesξ(t) that are nondecreasing and left continuous with respect tot,withξ(0)=0.
Next we present some preliminaries about the extension of the Malliavin calculus into the stochastic distribution space of Hida;for more details,we refer the reader to Aase et al.[1]and Di Nunno et al.[11].
The classical Malliavin derivative is only defined on a subspace D1,2of L2(P).However,there are many important random variables in L2(P) that do not belong to D1,2.For example,this is the case for the solutions of a backward stochastic differential equations or more generally the BSVIE.This is why the Malliavin derivative was extended to an operator defined on the whole of L2(P) and with values in the Hida space (S)*of stochastic distributions.It was proved by Aase et al.[1]that one can extend the Malliavin derivative operatorDtfrom D1,2to all of L2(FT,P) in such a way that,also denoting the extended operator byDt,for all random variableF∈L2(FT,P),we have that
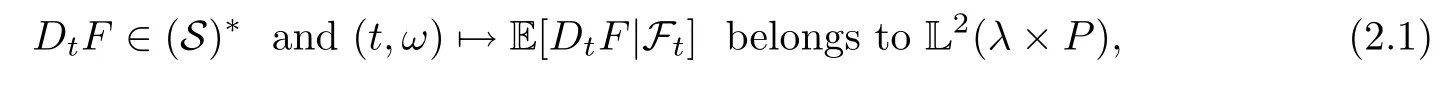
whereλis Lebesgue measure on[0,T].We now give a short introduction to Malliavin calculus and its extension to Hida-Malliavin calculus in the white noise setting.
Definition 2.1(i) LetF∈L2(P) and letγ∈L2(R) be deterministic.Then the directional derivative ofFin (S)*(respectively,in L2(P)) in the directionγis defined by
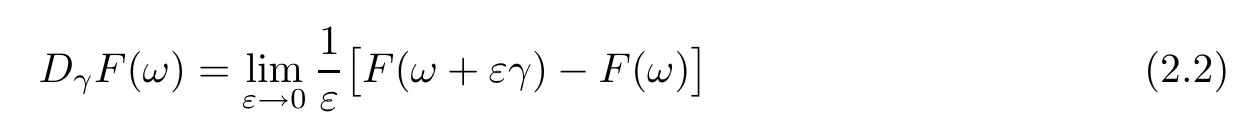
whenever the limit exists in (S)*(respectively,in L2(P)).
(ii) Suppose that there exists a functionψ:R(S)*(respectively,ψ:RL2(P)) such that
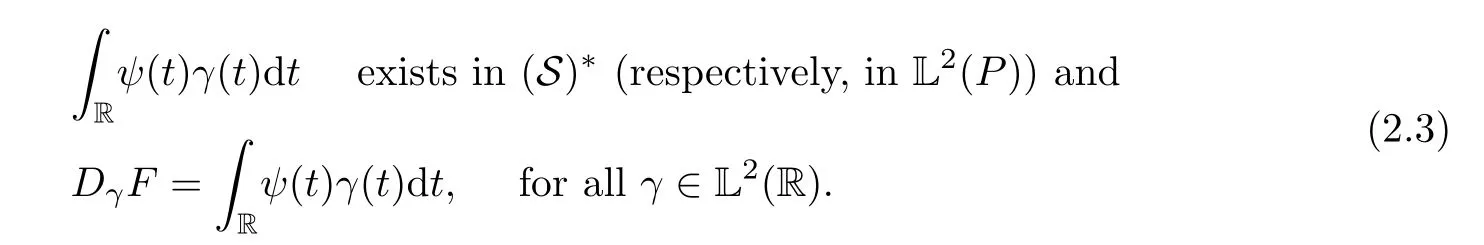
Then we say thatFis Hida-Malliavin differentiable in (S)*(respectively,in L2(P)) and we write

We callDtFthe Hida-Malliavin derivative attin (S)*(respectively,in L2(P)) or the stochastic gradient ofFatt.
LetF1,...,Fm∈L2(P) be Hida-Malliavin differentiable in L2(P).Suppose thatφ∈C1(Rm),DtFi∈L2(P),for allt∈R,and(F)D·Fi∈L2(λ×P) fori=1,...,m,whereF=(F1,...,Fm).Then,φ(F) is Hida-Malliavin differentiable and

For the Brownian motion,we have the following generalized duality formula:
Proposition 2.2Fixs∈[0,T]. Iftφ(t,s,ω)∈L2(λ×P) is F-adapted withandF∈L2(FT,P),then we have

We will need the following:
Lemma 2.3Lett,s,ωG(t,s,ω)∈L2(λ×λ×P) andt,ωp(t)∈L2(λ×P),then the followings hold:
1.The Fubini theorem combined with a change of variables gives
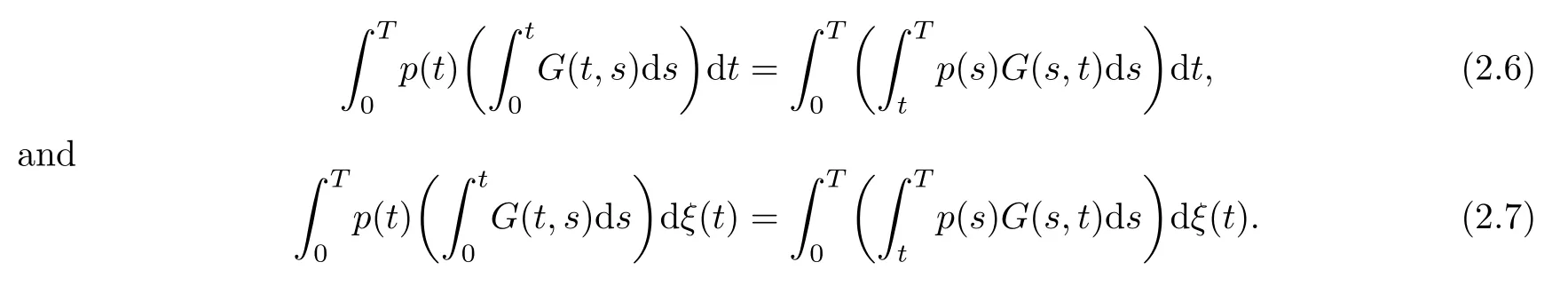
2.The generalized duality formula (2.5),together with the Fubini theorem,yields

3 Stochastic Maximum Principles
In this section,we study stochastic maximum principles of stochastic Volterra integral systems under partial information;that is,the information available to the controller is given by a sub-filtration G.Suppose that the state of our systemXu,ξ(t)=X(t) satisfies the following SVIE:
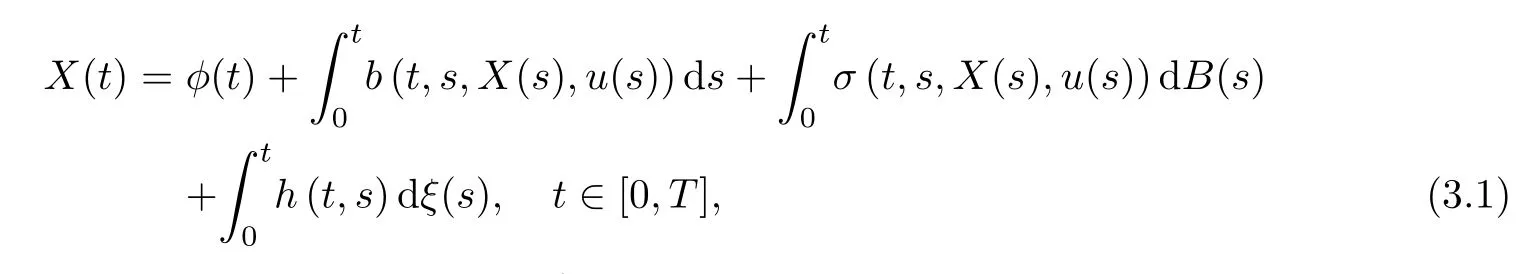
whereb(t,s,x,u)=b(t,s,x,u,ω):[0,T]2×R×U×Ω→R,σ(t,s,x,u)=σ(t,s,x,u,ω):[0,T]2×R×U×Ω→R.The performance functional has the form

with given functionsf0(t,x,u)=f0(t,x,u,ω):[0,T]×R×U×Ω→R,f1(t,x)=f1(t,x,ω):[0,T]×R×Ω→R andg(x)=g(x,ω):R×Ω→R.We study the following problem:
Problem 3.1Find a control pairsuch that

We impose the following assumptions on the coefficients:
The processesb(t,s,x,u),σ(t,s,x,u),f0(s,x,u),f1(t,x,ξ) andh(t,s) are F-adapted with respect tosfor alls≤t,and twice continuously differentiable (C2) with respect tot,x,and continuously differentiable (C1) with respect toufor eachs.The drivergis assumed to be FT-measurable and (C1) inx.Moreover,all the partial derivatives are supposed to be bounded.
Note that the performance functional (3.2) is not of Volterra type.
3.1 The Hamiltonian and the adjoint equations
Define the Hamiltonian functional,associated to our control problem (3.1) and (3.2),as

For convenience,we will use the following notation from now on:
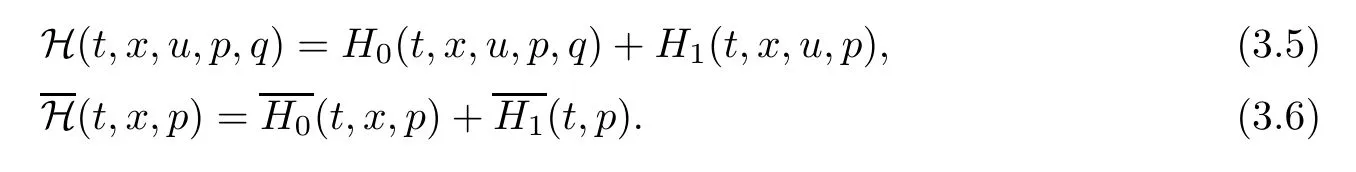
The BSVIE for the adjoint processesp(t),q(t,s) is defined by

where we have used the following simplified notation:
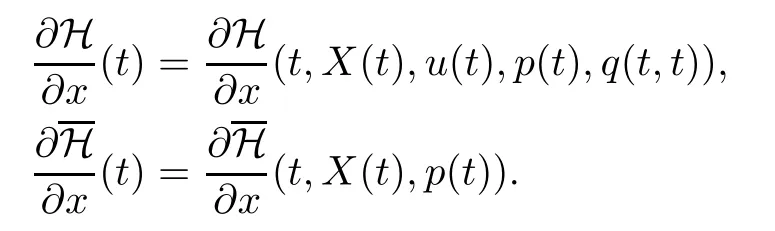
Note that from equation (3.1),for each (t,s)∈[0,T]2,we get the following equivalent formulation:
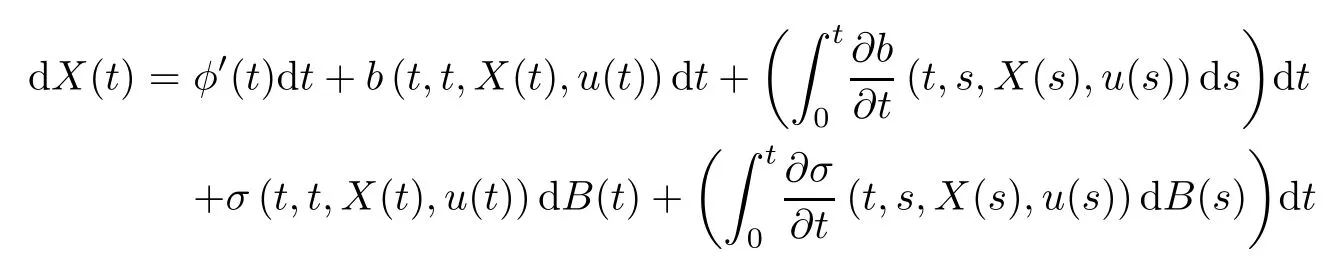


under which we can write the following differential form of equation (3.7):
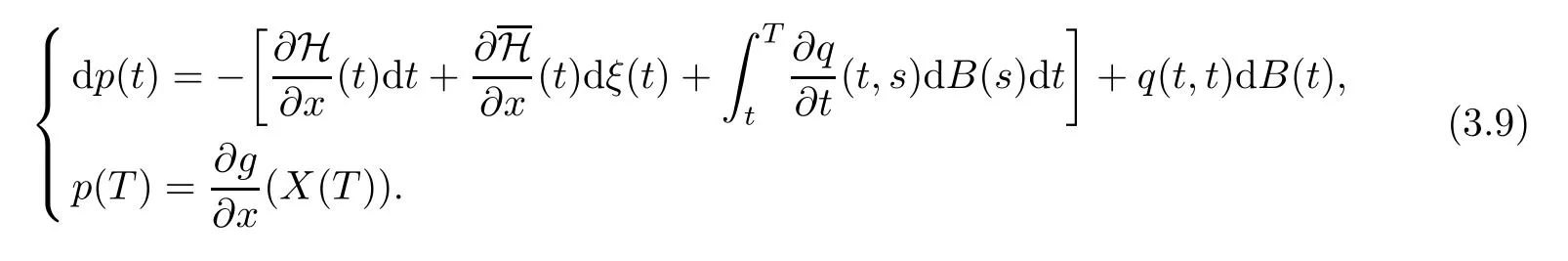
3.2 A sufficient maximum principle
We will see that under which conditions the couple (u,ξ) is optimal;that is,we will prove a sufficient version of the maximum principle approach (a verification theorem).
·Maximum condition foru
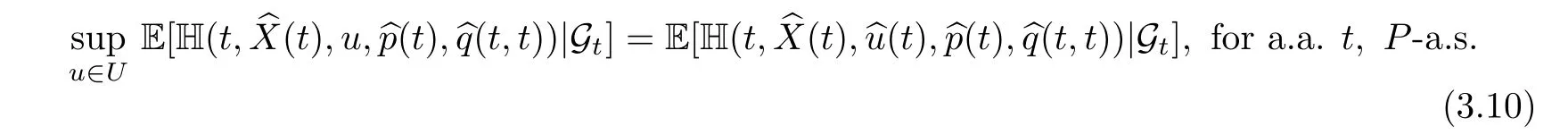
where we are using the notation
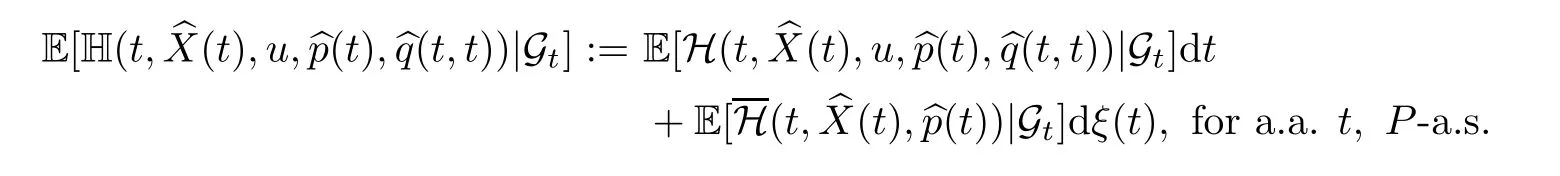
·Maximum condition forξ
For allξ∈K we have,in the sense of inequality between random measures,
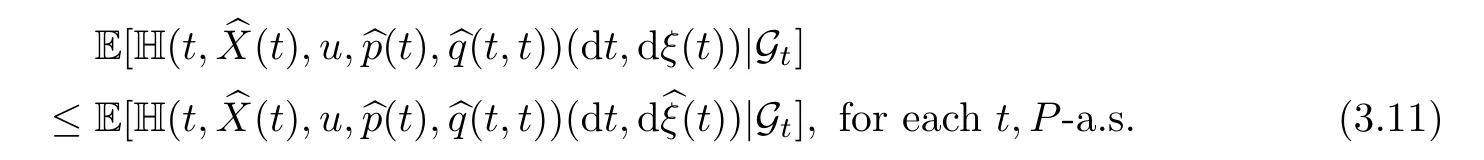
ProofChoosingu∈A andξ∈K,we want to prove thatWe set
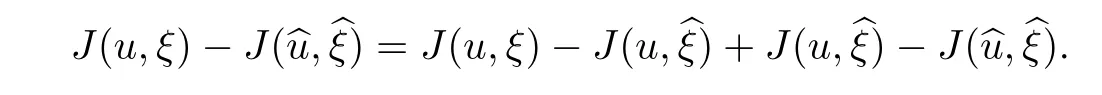
Since we have one regular control and one singular,we will solve the problem by separating them as follows:
As he spoke less, he heard more. He heard people talking and telling stories. He heard a woman saying that an elephant jumped over a fence. He also heard a man saying that he had never made a mistake.
First,we prove thatξis optimal;that is,for all fixedu∈U;Then,we plug the optimalinto the second part and we prove it foru,that is,However,the case of regular controlsuwas proved in Theorem 4.3 by Agram et al.[4].It rests to prove only the inequality for singular controlsξ.
From definition (3.2),we have

where we have used hereafter the following shorthand notations:

By concavity ofg,together with the terminal value of the BSVIE (3.7),we obtain

Applying the integration by parts formula to the product,we get

It follows from formulas (2.6)–(2.8) that
Substituting the above into (3.12),we obtain

Using the concavity of H and H with respect toxandξ,we have
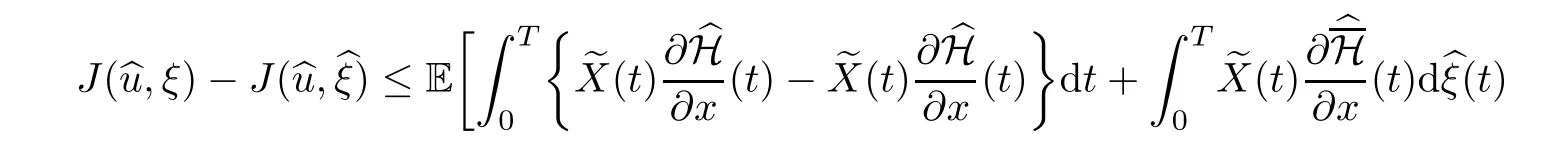
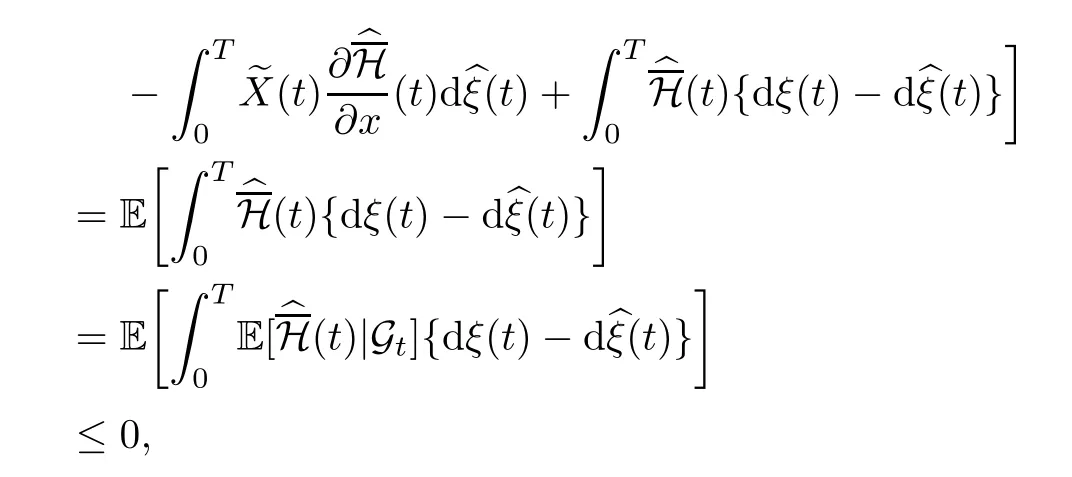
where the last inequality holds because of the maximum condition (3.11).We conclude that

The proof is complete. □
3.3 A necessary maximum principle
Since the concavity condition is not always satisfied,it is useful to have a necessary condition of optimality,where this condition is not required.Suppose that a control (bu,bξ)∈A×K is an optimal pair and that (v,ζ)∈A×K.Defineuλ=u+λvandξλ=ξ+λζ,for a non-zero sufficiently smallλ.Assume that (uλ,ξλ)∈A×K.For each givent∈[0,T],letη=η(t) be a bounded Gt-measurable random variable,leth∈[T-t,T],and define

Assume that the derivative processY(t),defined byexists.Then we see that
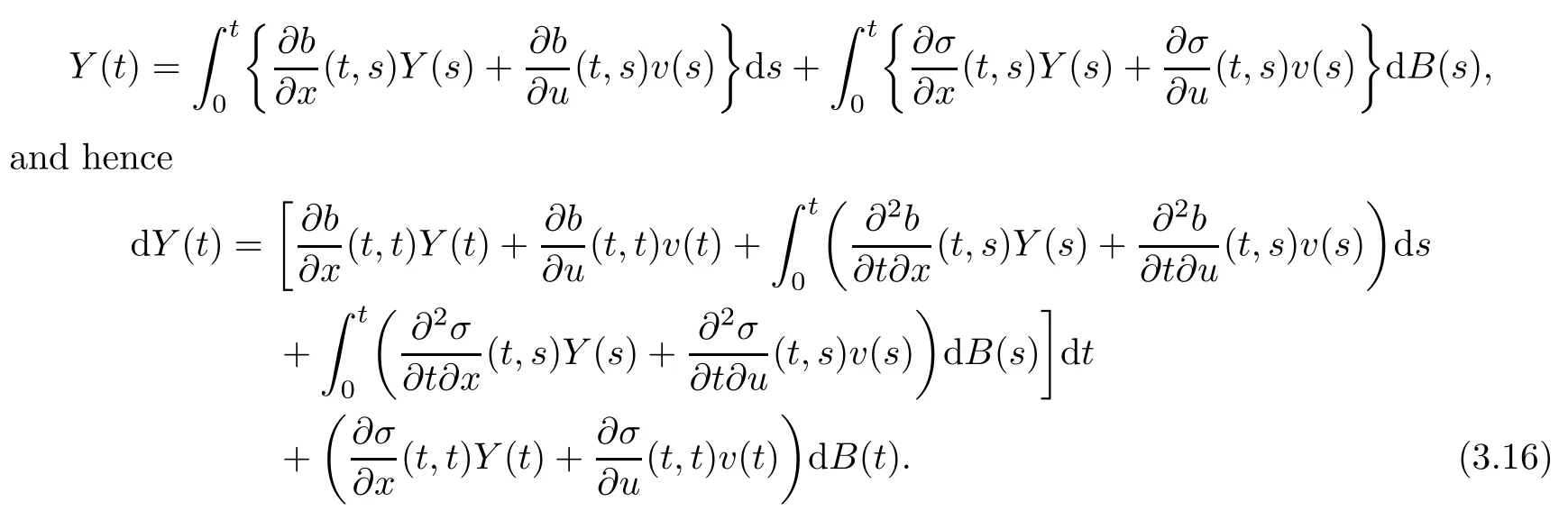
Similarly,we define the derivative processas follows:
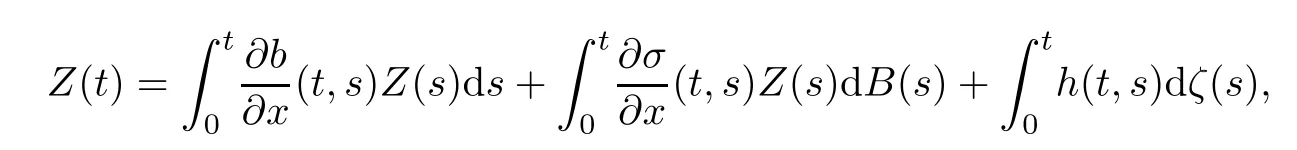
which is equivalent to
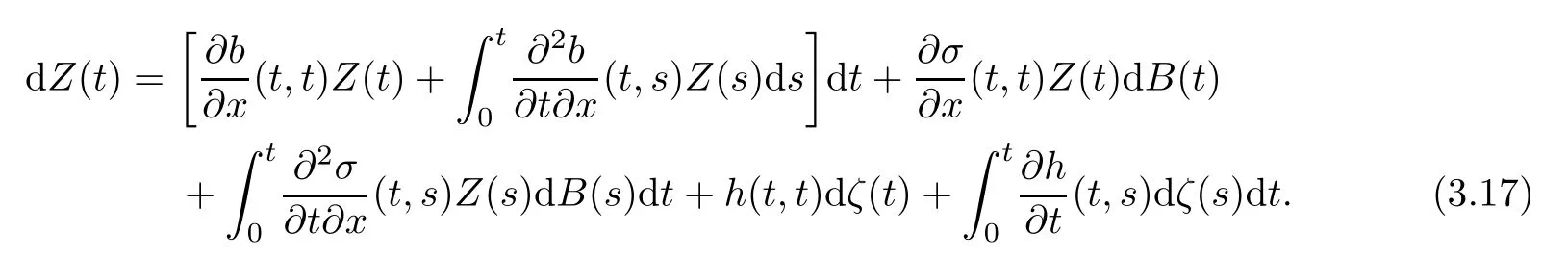
We shall prove the following theorem:
Theorem 3.3(Necessary maximum principle)
1.For fixedξ∈K,suppose that∈A is such that,for allβas in (3.15),

and the corresponding solutionof (3.1) and (3.7) exists.Then,

2.Conversely,if (3.19) holds,then (3.18) holds.
3.Similarly,for fixed∈A,suppose that∈K is optimal.Then the following variational inequalities hold:
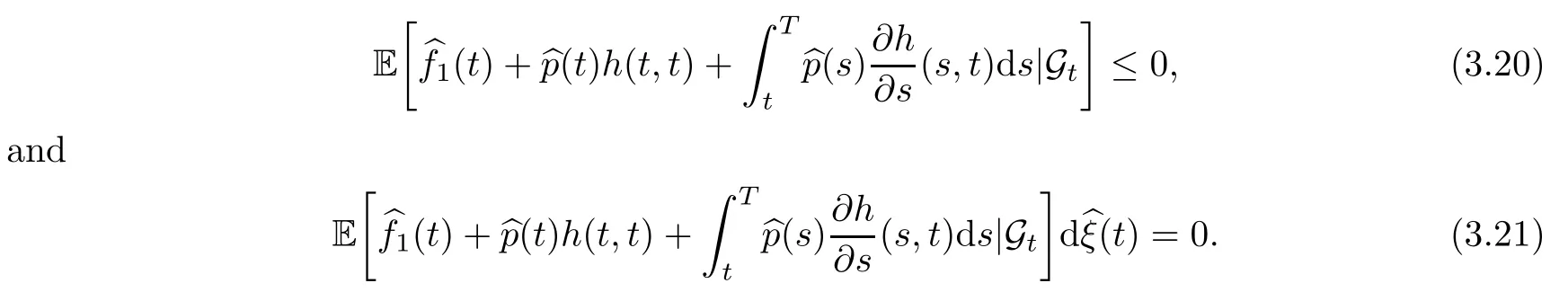
ProofFor simplicity of notation,we drop the“hat”notation in the following.Points 1-2 are direct consequence of Theorem 4.4 in Agram et al.[4].We proceed to prove point 3.Sinceis fixed,we drop the hat from the notation.Set

Therefore,from (2.6)–(2.8),we obtain
Using the definition of H andin (3.5)–(3.6),
If we chooseζto be a pure jump process of the form,whereα(ti)>0 is Gti-measurable for allti,thenζ∈K () and (3.23) gives
Since this holds for all suchζwith arbitraryti,we conclude that
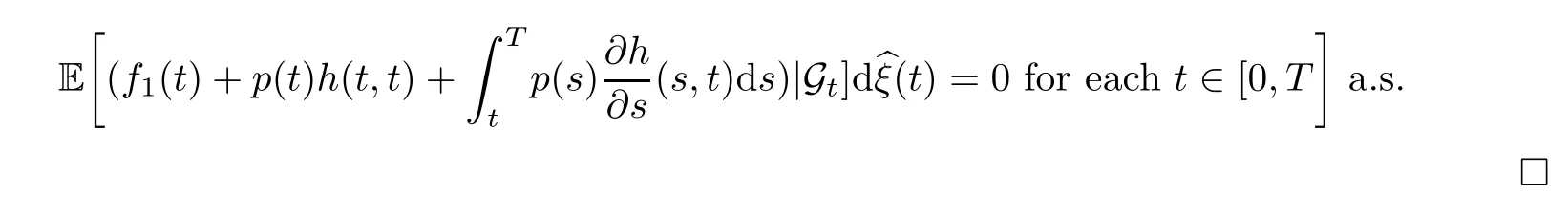
4 Application to Optimal Harvesting With Memory
4.1 Optimal harvesting with density-dependent prices
LetXξ(t)=X(t) be a given population density (or cash flow) process,modelled by the following stochastic Volterra equation:

or,in differential form,

We see that the dynamics ofX(t) contains a history or memory term represented by theds-integral.
We assume thatb0(t,s) andσ0(s) are given deterministic functions oft,s,with values in R,and thatb0(t,s),h(t,s) are continuously differentiable with respect totfor eachsandh(t,s)>0.For simplicity,we assume that these functions are bounded,and the initial valuex0∈R.
We want to solve the following maximisation problem:
Problem 4.1Find∈K,such that

Here,θ=θ(ω) is a given FT-measurable square integrable random variable.
In this case,the Hamiltonian H takes the form
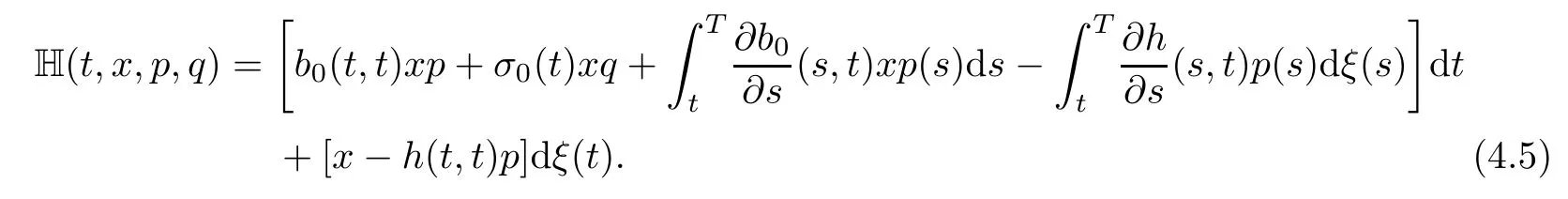
Note that H is not concave with respect tox,so the sufficient maximum principle does not apply.However,we can use the necessary maximum principle as follows:The adjoint equation takes the form
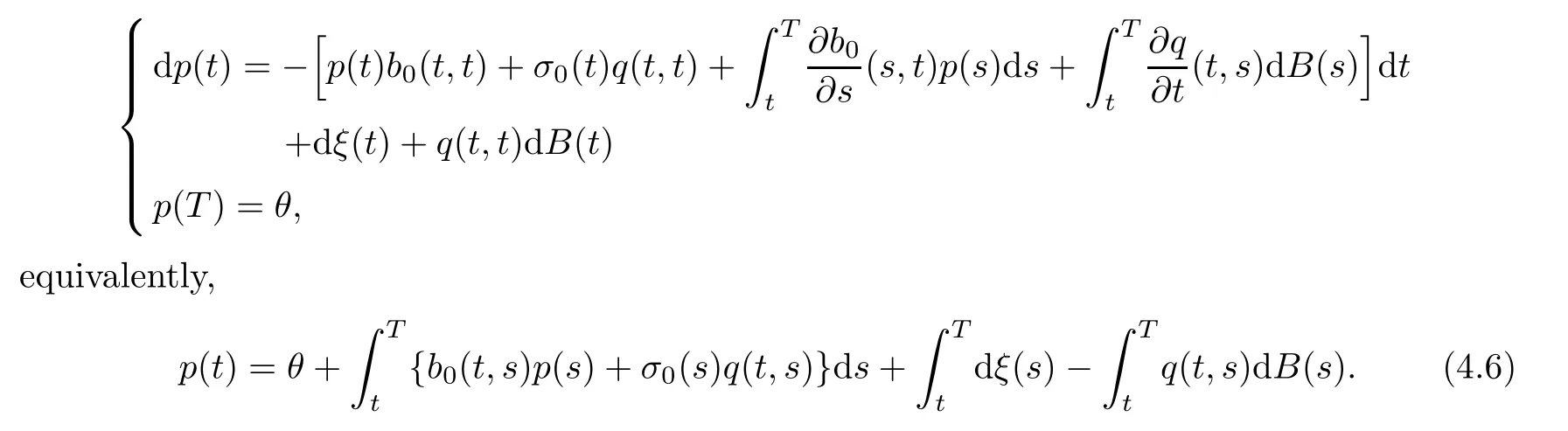
The variational inequalities for an optimal controland the correspondingare as follows:
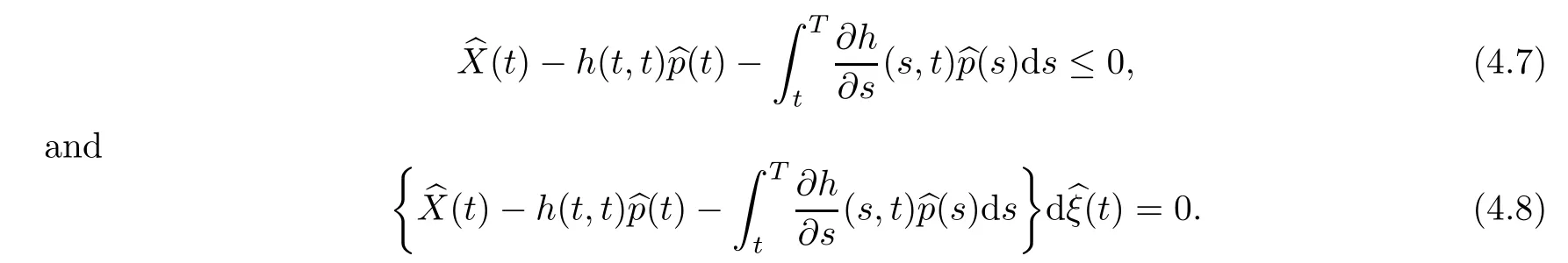
We have proved
Theorem 4.2Suppose thatis an optimal control for Problem 4.1,with corresponding solutionof (4.1).Then,(4.7) and (4.8) hold,that is,
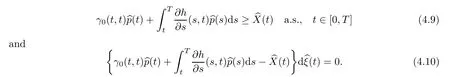
Remark 4.3The above result states thatincreases only when
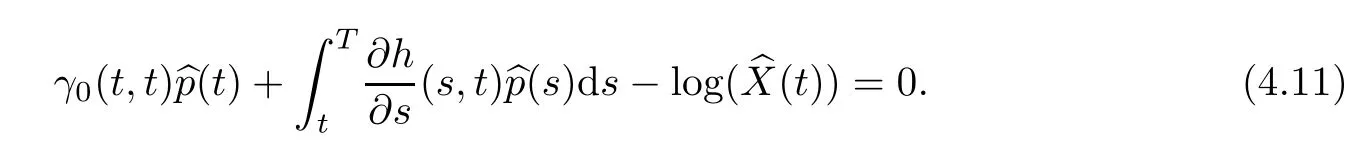
Combining this with (4.7),we can conclude that the optimal control can be associated to the solution of a system of reflected forward-backward SVIEs with barrier given by (4.9).
In particular,if we chooseh=1,the variational inequalities become

Remark 4.4This is a coupled systemconsisting of the solutionX(t) of the singularly controlled forward SDE

4.2 Optimal harvesting with density-independent prices
Consider again equation (4.14),but now with performance functional

for some positive deterministic functionρ.We want to find an optimal∈K,such that
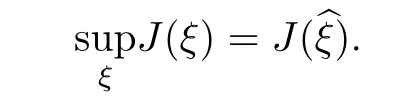
In this case,the Hamiltonian H gets the form

Note that H (x) is concave in this case.Therefore,we can apply the sufficient maximum principle here.The adjoint equation gets the form

A closed form expression forp(t) is given in Appendix (Theorem 5.1).
In this case,the variational inequalities for an optimal controland the correspondingare as follows:

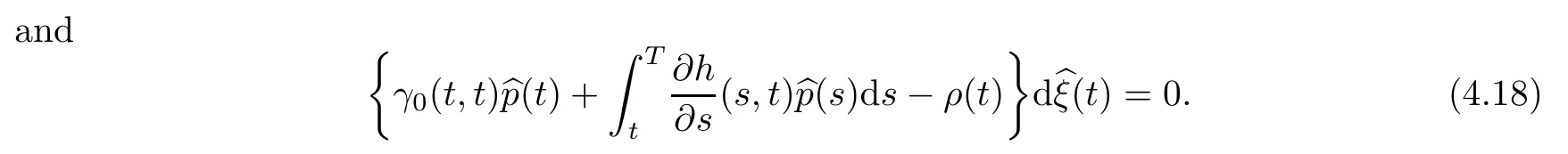
We have proved
Theorem 4.5Suppose thatwith corresponding solution bp(t) of the BSVIE (4.16) satisfies the equations (4.17)–(4.18).Then,bξis an optimal control for Problem 4.1.
Remark 4.6Note that (4.17)–(4.18) constitute a sufficient condition for optimality.We can for example get this equation satisfied by choosingas the solution of the BSVIE (4.16) reflected downwards at the barrier given by

5 Appendix
Theorem 5.1Consider the next linear BSVIE with singular drift

The first componentp(t) of the solution (p(t),q(t)) can be written in closed formula as follows:
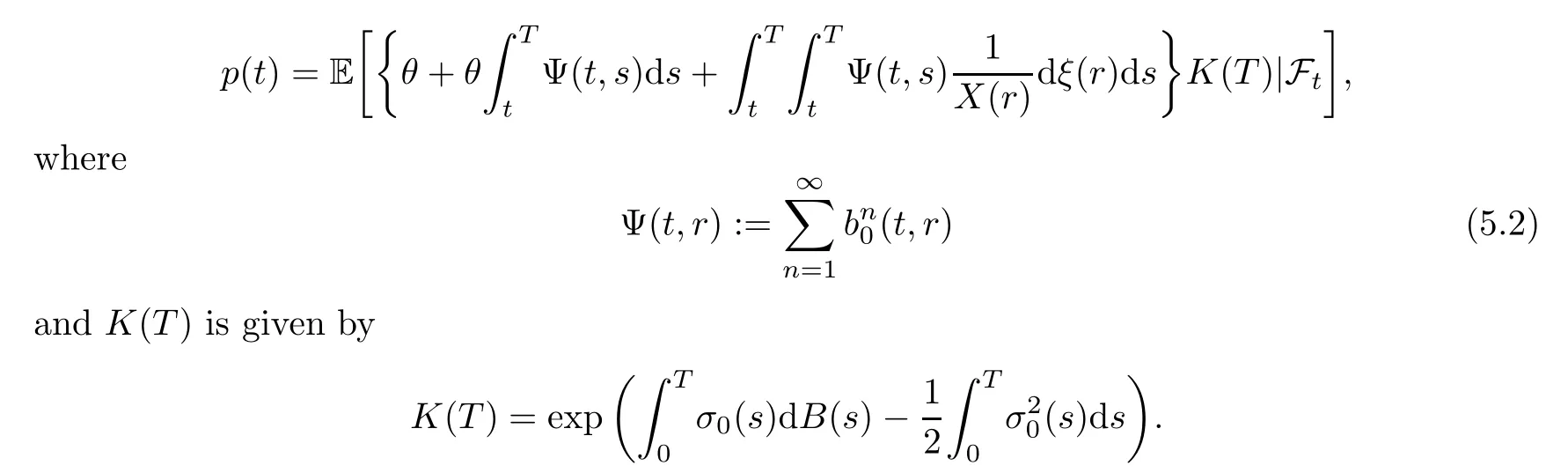
ProofThe proof is an extension of Theorem 3.1 in Hu and Øksendal[9]to BSVIE with singular drift.
Define the measureQby

whereM(t) satisfies the equation

which has the solution
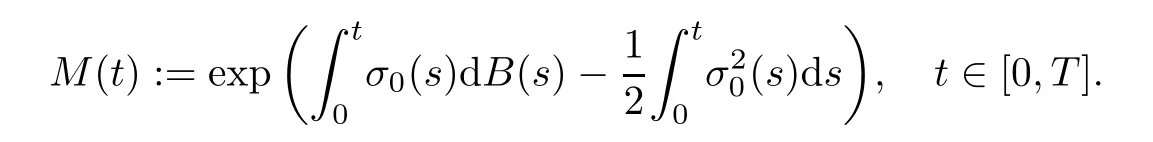
Then under the measureQ,the process
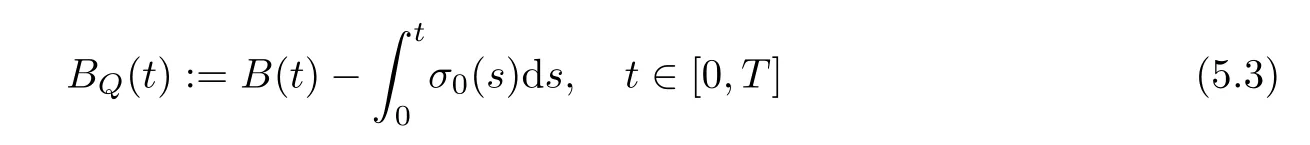
is aQ-Brownian motion.
For all 0≤t≤r≤T,define
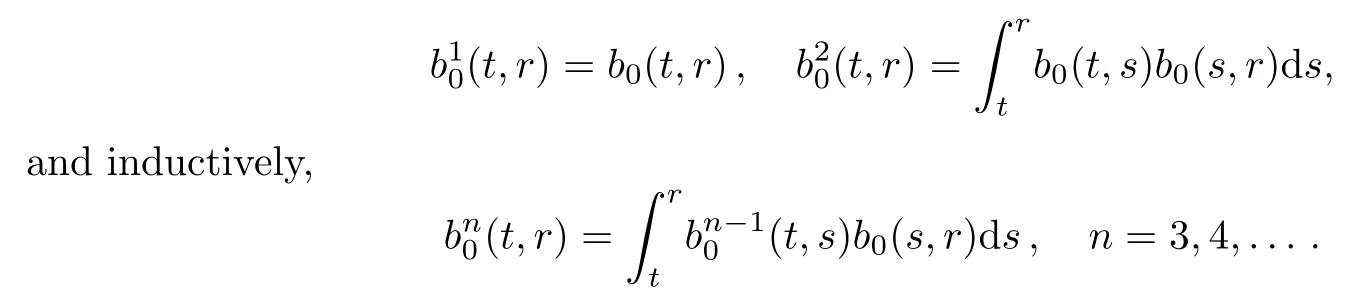
Note that if|b0(t,r)|≤C(constant) for allt,r,then by induction onn∈N:for allt,r,n.Hence,

for allt,r.By changing of measure,we can rewrite equation (4.15) as

where the processBQis defined by (5.3).Taking the conditionalQ-expectation on Ft,we get

Fixr∈[0,t].Taking the conditionalQ-expectation on Frof (5.5),we get
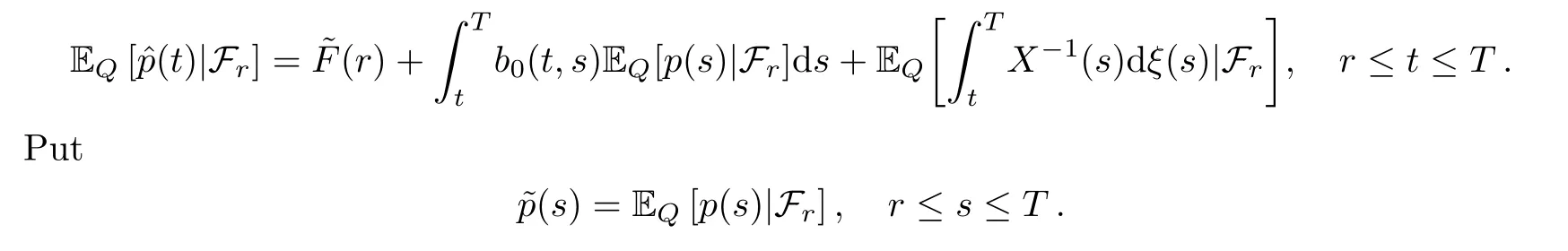
Then,the above equation can be written as
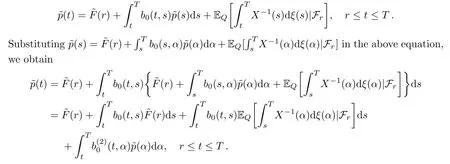
Repeating this,we get by induction

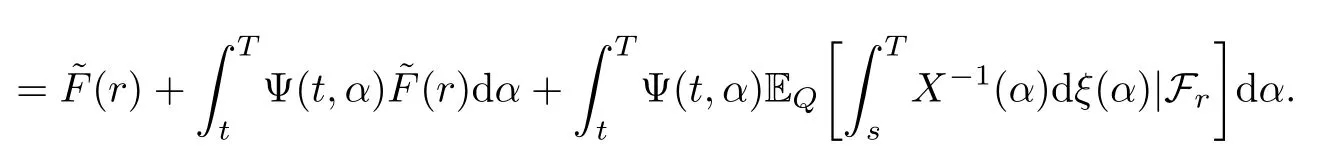
where Ψ is defined by (5.2).Now substituting~p(s) in (5.5),forr=t,we obtain
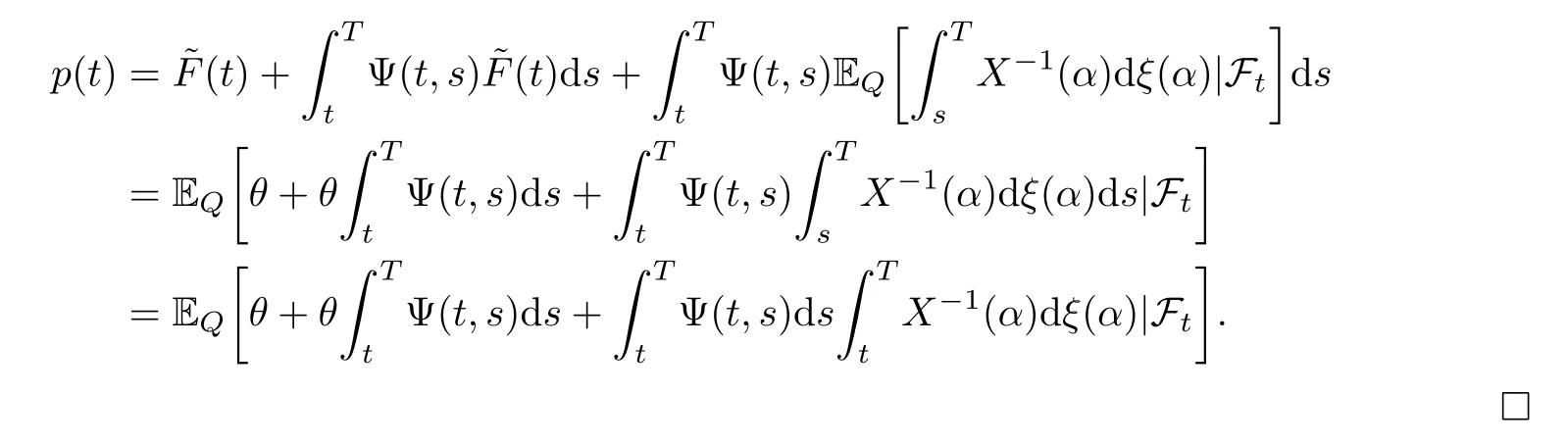
 Acta Mathematica Scientia(English Series)2022年3期
Acta Mathematica Scientia(English Series)2022年3期
- Acta Mathematica Scientia(English Series)的其它文章
- A ROBUST COLOR EDGE DETECTION ALGORITHM BASED ON THE QUATERNION HARDY FILTER*
- CONTINUOUS SELECTIONS OF THE SET-VALUED METRIC GENERALIZED INVERSE IN 2-STRICTLY CONVEX BANACH SPACES*
- EXISTENCE RESULTS FOR SINGULAR FRACTIONAL p-KIRCHHOFF PROBLEMS*
- BOUNDS FOR MULTILINEAR OPERATORS UNDER AN INTEGRAL TYPE CONDITION ON MORREY SPACES*
- LEARNING RATES OF KERNEL-BASED ROBUST CLASSIFICATION*
- A COMPACTNESS THEOREM FOR STABLE FLAT SL (2,C) CONNECTIONS ON 3-FOLDS*
