基于优化非线性自回归神经网络模型的水质预测

唐亦舜， 徐 庆， 刘振鸿， 高 品

(1.东华大学 环境科学与工程学院， 上海 201620； 2.上海市环境监测中心， 上海 200235)

因化学品泄露等原因引发的水质污染事件频发[1-3]，造成严重的环境污染和社会影响。水质预测已成为环境监测领域的关注焦点，对地表水环境进行有效管理是至关重要的[4]。河流水质预测是区域水环境管理的基础[5]，通过对一定区域的河流水质参数变化情况进行实时监测，结合当地水质状况、生态环境状况、污染物迁移特性和经济发展等实际情况预测未来水质变化趋势[6]。尽管如此，水质预测研究仍处于发展阶段[7]，如何有效利用现有庞大的在线监测数据提高水质预测精度，是构建水质预测模型亟需解决的关键问题。

随着人工智能技术的迅速发展，人工神经网络(artificial neural network, ANN)因其优异的非线性关系处理能力、较高的预测准确度和较强的复杂水质适应性等，成为国内外水质预测模型的热点研究方法[8-9]。其中，非线性自回归(nonlinear auto-regressive, NAR)神经网络具有反馈与记忆功能，以自身为回归变量，每一时刻的输出都是当下时刻之前系统内随机变量的线性组合，具有动态性与综合性特征[10-11]，在时间序列动态建模预测方面具有明显优势。虽然NAR神经网络已被广泛应用于交通运输[12-13]、空气质量[14]、社会经济[15-16]等领域，但在水质预测方面的应用研究还较少。本文以上海市某支流具有代表性的监测断面为研究对象，通过试验法优化确定输入数据段和模型参数，采用不同指标对模型预测性能和预测效果进行对比评价以改进NAR神经网络模型，并将改进的NAR神经网络模型用于预测pH、溶解氧(dissolved oxygen, DO)质量浓度和浊度等水质指标，以期为水质的预测预警提供技术支撑。

1 研究方法

1.1 NAR神经网络

NAR神经网络属于处理时间序列的动态神经网络模型，其每一个时刻的输出都是先前全部输入的综合描述，可通过输入/输出关系进行不断调整，具有反馈记忆功能和动态综合性特征。NAR神经网络模型一般由输入层、带有延迟的隐含层和输出层构成，如图1所示，输入层时间序列y(t)进入带有延迟的隐含层，隐含层为一层或多层的神经元，经训练、传递和学习后，最终到达输出层，并传递模型结果[10]。

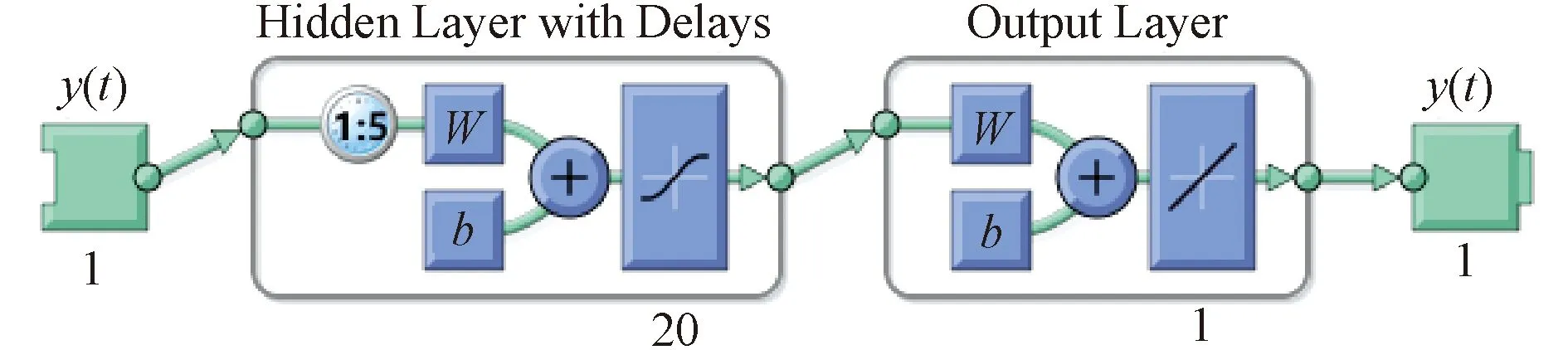
注：1∶5表示延迟阶数为5；20为隐含层神经元数； W为权值；b为阈值。图1 NAR神经网络结构Fig.1 Structure of NAR neural network

对于时间序列{y(t)}，t=1,2,3,…,n，NAR神经网络模型表达式如式(1)所示。

y(t)=f(y(t-1),y(t-2),y(t-3),…,

y(t-n))+ε(t)

(1)

式中：n为输入延迟阶数；f(·)为传递函数，神经网络训练的目的是通过优化网络权值和神经元偏置进行函数估计；ε(t)为y(t)的扰动项，属随机白噪声，但其与前一时刻时间序列y(t-1)无关[17-18]。

1.2 数据来源与预处理

1.2.1 数据来源

本文研究数据源于上海市某支流具有代表性的监测断面的水质监测结果，选取2019年1月1日—12月1日的水质监测数据，水质指标包括pH、DO质量浓度和浊度。由于原始数据监测频率存在差异，本文统一以4 h间隔对原始数据进行筛选，每天共6组数据。

1.2.2 缺失数据填补

针对前后时间间隔较小的缺失数据，考虑到DO质量浓度具有周期性变化特点，选用前1 d同一时刻与其前后时间点的3组数据平均值进行填补，即若缺失数据为第i点，其替代值可通过式(2)获得。此外，针对时间间隔较大的缺失数据，则采用天气状况相似的临近日期的同一时刻数据进行补全。

(2)

1.2.3 异常数据剔除

通常异常数据主要由过失误差所导致。过失误差是指由非随机事件如工艺泄漏、测量仪表失灵、设备故障等引发的测量数据严重失真导致数据真实值与实测值之间出现的显著差异。一般根据拉依达准则剔除异常数据。

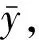
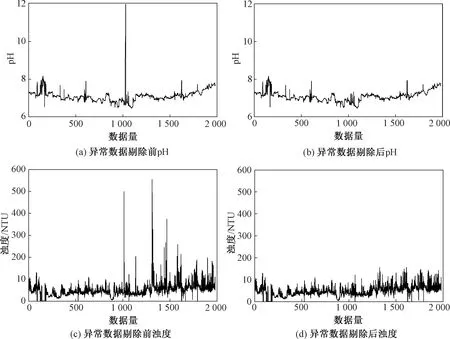
图2 剔除异常数据前后的pH和浊度Fig.2 pH and turbidity before and after abnormal data removal

图3 DO质量浓度变化趋势Fig.3 Variation trend of DO mass concentration

1.2.4 数据归一化处理

将有量纲表达式转化为无量纲表达式，通常需对输入数据作归一化处理。本文采用最大最小值法进行数据归一化，将原始数据线性化转换到[0,1]，归一化方法如式(3)所示。

(3)

1.3 神经网络设计

采用试验法确定NAR神经网络模型的延迟阶数和隐含层神经元数，输入样本数据对模型进行训练并进行误差计算和模型检验，通过调整网络结构获得最佳预测模型。

1.3.1 试验法

试验法即根据经验对某一输入参数设置不同值进行多次模拟预测，通过比较分析预测结果选择最优结果对应的输入值作为该参数的初始输入值。

1.3.2 模型评价指标

采用相关系数r、纳什效率系数(Nash-Sutcliffe efficiency coefficient, NSE)、均方根误差(root mean squared error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)评价模型预测性能。

r用于评价变量之间的相关程度，对于两组变量X和Y，其定义式如式(4)所示。

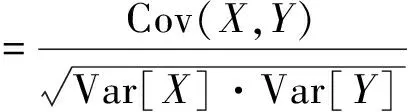
(4)

式中：Cov(X,Y)为X与Y的协方差；Var[X]和Var[Y]分别为X和Y的方差；|r|≤1，|r|越大，X和Y之间相关性越强。

NSE用于评价模型预测效果，表达式如式(5)[19]所示。

(5)

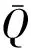
RMSE用于衡量模型预测值与实测值之间的偏差，表达式如式(6)所示。

(6)

MAPE是平均绝对偏差(mean absolute deviation, MAD)的变形，其消除了原始数据绝对大小对MAD的影响，是衡量模型预测准确性的统计指标，计算公式如式(7)所示。

(7)

式中：EMAPE∈[0,+∞)，EMAPE>100%表明预测模型为劣质模型。若存在真实值为0的数据，则该式不再适用，因此在计算EMAPE时需先对原始数据进行反归一化处理。

1.3.3 检验方法

采用Ljung-Box Q-test(LBQ)法检验某一时段内时间序列预测值是否为随机独立值，若预测值不是彼此独立的，则多个预测值之间存在关联性，这将使得整体时间序列具有自相关性。通常这种自相关性会降低基于时间序列模型的预测准确度，并导致模型对数据的错误解释，故采用LBQ法评估NAR神经网络模型的拟合结果，以确保预测残差彼此独立[10]。LBQ检验的统计结果计算方法如式(8)所示。

(8)

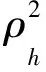
1.3.4 输入数据段选取

神经网络输入时间序列的波动程度、时间跨度、完整性等对其输出的影响非常大，训练数据不足造成机器学习不充分导致欠拟合，但过量的样本输入则会使模型陷入过分学习，在影响学习效率的同时还会导致过拟合，降低模型预测精度。本文以2019年11月30日监测数据为样本终点，分别以11月16日、11月1日、10月16日、10月1日、9月16日和9月1日的监测数据为样本起点，对应的样本量分别为90、180、270、360、450和540，以不同数据段预测12月1日的相应指标值，以各评价指标与检验结果为依据对比模型整体性能和预测精度，进而确定输入数据段。为方便计算，对12月1日的预测值进行反归一化处理。

设置训练集、验证集和测试集的比例为70%、15%和15%，延迟阶数为2，隐含层神经元数为10，训练次数为10，优化选取数据段。图4 和表1为pH、DO质量浓度和浊度的预测结果，采用LBQ法进行统计检验，可得逻辑值h、概率值p、检验统计量s和临界值c，其中：h=0表示拒绝原假设，即残差序列无自相关性，h=1表示存在自相关性；p越小、s越大，表明自相关性越强。检验结果见表2。

图4 不同输入数据量下pH、DO质量浓度和浊度的ERMSE和EMAPEFig.4 ERMSE and EMAPE for pH, DO mass concentration and turbidity with different input data volumes

由图4、表1和表2可知，选取2019年11月1日—11月30日时间序列共180个数据点进行模型训练时，模型对pH、DO质量浓度和浊度的预测效果最好，预测RMSE值分别为0.054、0.424 mg/L和20.960 NTU，MAPE值分别为0.58%、4.83%和20.33%。LBQ检验结果表明，在最佳数据段下只有浊度预测残差仍具有自相关性，可通过调整模型参数对模型进行优化，进一步提高预测精度。

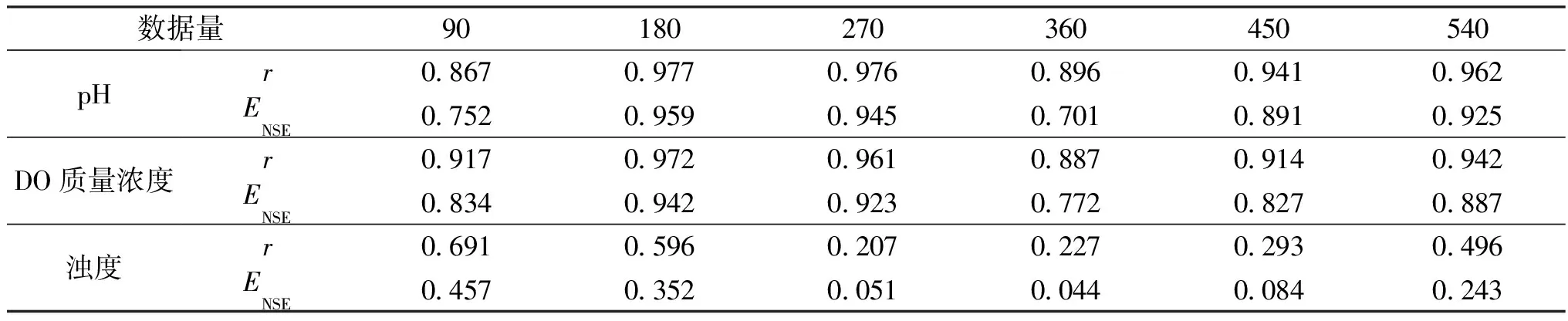
表1 不同输入数据量下pH、DO质量浓度和浊度的r和ENSETable 1 Results of r and ENSE for pH, DO mass concentration and turbidity with different input data volumes

表2 不同输入数据量下pH、DO质量浓度和浊度预测值的LBQ检验结果

1.3.5 模型参数确定

NAR神经网络延迟阶数和隐含层神经元数的选取尚无成熟的理论依据，通常只能根据经验或试验来确定[20-21]。

(1)延迟阶数。选定输入时间序列为2019年11月1日—11月30日的监测数据，保持训练集、验证集和测试集不变，隐含层神经元数为10，训练次数为10，调整延迟阶数，对比分析不同延迟阶数下pH、DO质量浓度和浊度预测性能及检验结果，如图5、表3～6所示。

从图5、表3和表4可以看出，由于原始数据的差异，pH、DO质量浓度和浊度预测模型的最佳延迟阶数分别为2、3和9，在最佳延迟阶数下，预测模型对pH、DO质量浓度和浊度的预测精度均得到提高，其中浊度的预测RMSE值从20.960 NTU降至17.940 NTU。由表5可知，pH和DO质量浓度预测结果均通过LBQ检验，而浊度预测模型较调整延迟阶数前可消除预测残差时间序列的显著自相关性(见表6)，使得预测结果从不可接受变为可接受。

表3 不同延迟阶数下pH和DO质量浓度的r和ENSETable 3 Results of r and ENSE for pH and DO mass concentration with different delay orders

表4 不同延迟阶数下浊度的r和ENSETable 4 Results of r and ENSE for turbidity with different delay orders

表5 不同延迟阶数下pH和DO质量浓度预测值的LBQ检验结果Table 5 LBQ test results of pH and DO mass concentration with different delay orders

表6 不同延迟阶数下浊度预测值的LBQ检验结果Table 6 LBQ test results of turbidity with different delay orders

图5 不同延迟阶数下pH、DO质量浓度和浊度的ERMSE和EMAPEFig.5 ERMSE and EMAPE for pH, DO mass concentration and turbidity with different delay orders

(2)隐含层神经元数。采用相同训练数据集，选取pH、DO质量浓度和浊度预测模型的延迟阶数分别为2、3和9，通过调整隐含层神经元数，重复上述预测步骤，对比分析pH、DO质量浓度和浊度预测性能及检验结果，确定最佳隐含层神经元数，如图6和表7所示。

从图6和表7可以看出，pH、DO质量浓度和浊度的预测RMSE和MAPE值均先减小后增大，而r和NSE值则相反，在模型隐含层神经元数为10时，预测RMSE、MAPE、r和NSE值几乎均达到极值，且预测残差也均通过LBQ检验(见表8)，隐含层神经元数过低，易出现拟合不足和容错性差等问题，但数量过多同样会造成过拟合现象，并显著增加模型迭代次数和训练时间。

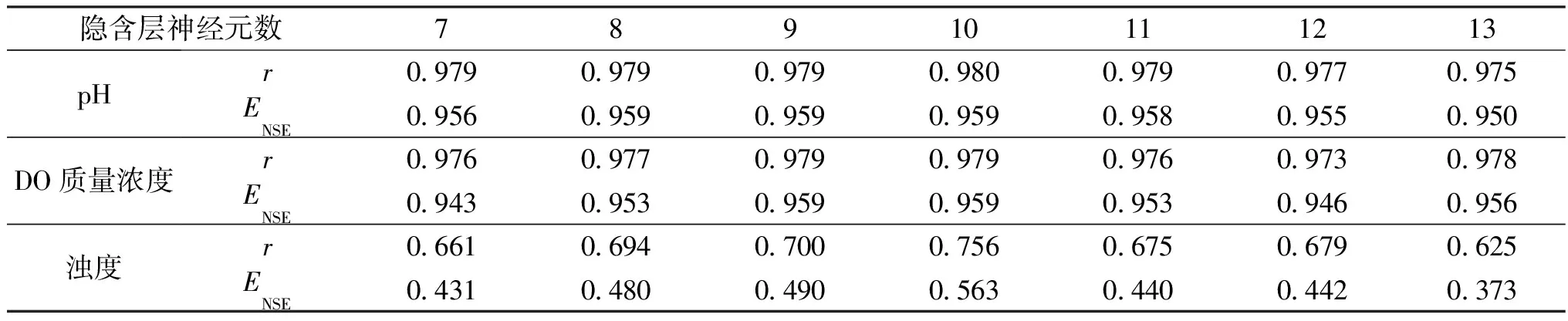
表7 不同隐含层神经元数下pH、DO质量浓度和浊度的r和ENSETable 7 Results of r and ENSE for pH, DO mass concentration and turbidity with different numbers of hidden layer neuron

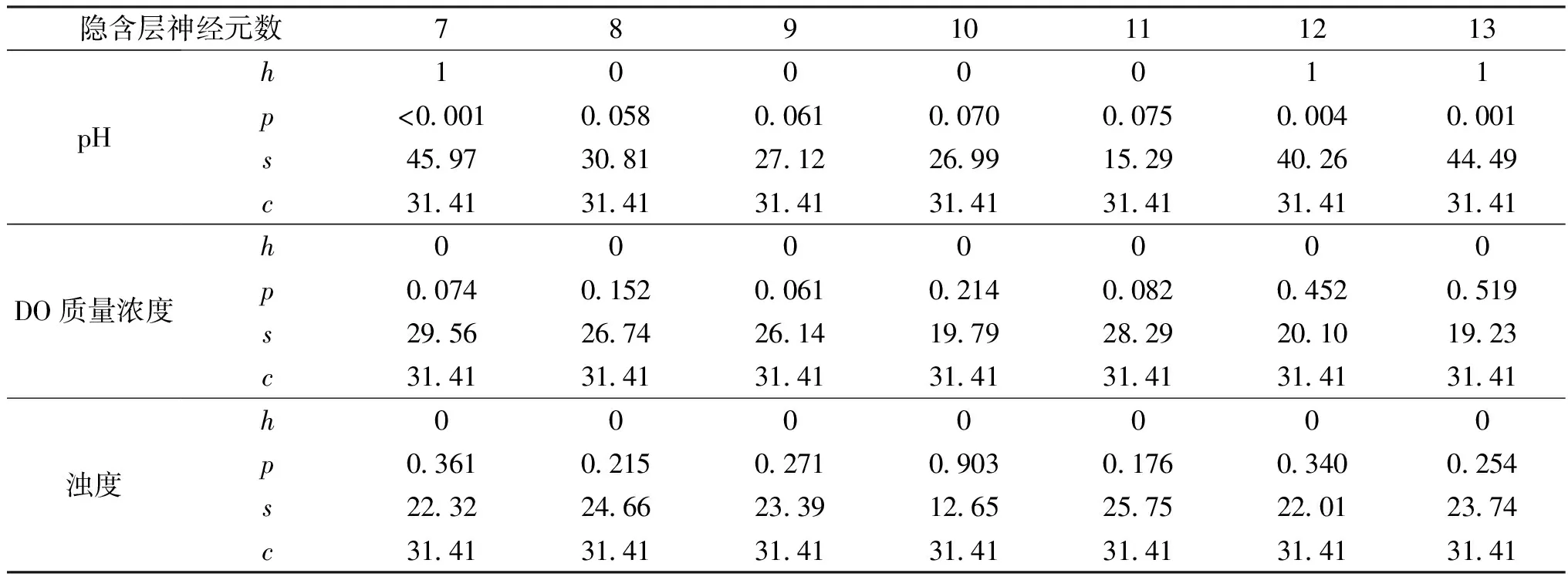
表8 不同隐含层神经元数下pH、DO质量浓度和浊度预测值的LBQ检验结果Table 8 LBQ test results of pH, DO mass concentration and turbidity with different numbers of hidden layer neuron

图6 不同隐含层神经元数下pH、DO质量浓度和浊度的ERMSE和EMAPEFig.6 ERMSE and EMAPE for pH, DO mass concentration and turbidity with different numbers of hidden layer neuron

2 模型预测结果分析

2.1 模型构建

基于上述优化结果，确定pH、DO质量浓度和浊度预测模型结构参数如下：各指标预测模型输入样本时间序列均为2019年11月1日—11月30日，训练集、测试集和验证集分别占70%、15%和15%，pH、DO质量浓度和浊度预测模型的延迟阶数分别为2、3和9，隐含层神经元数均为10。采用Levenberg-Marquardt(L-M)算法训练网络模型，训练函数为trainlm，传递函数为tansig，权值自适应学习函数为learngd。

2.2 预测结果与误差分析

为评价模型预测效果和实际应用效果，以目标监测断面2019年11月2日—12月1日监测数据为训练样本，预测12月2日pH、DO质量浓度和浊度。由于输入权值和阈值会影响神经网络性能，因此各模型在表4模型结构参数下训练20次，预测结果如图7所示，同时对比分析6个预测点的RMSE与MAPE值(见表9)。

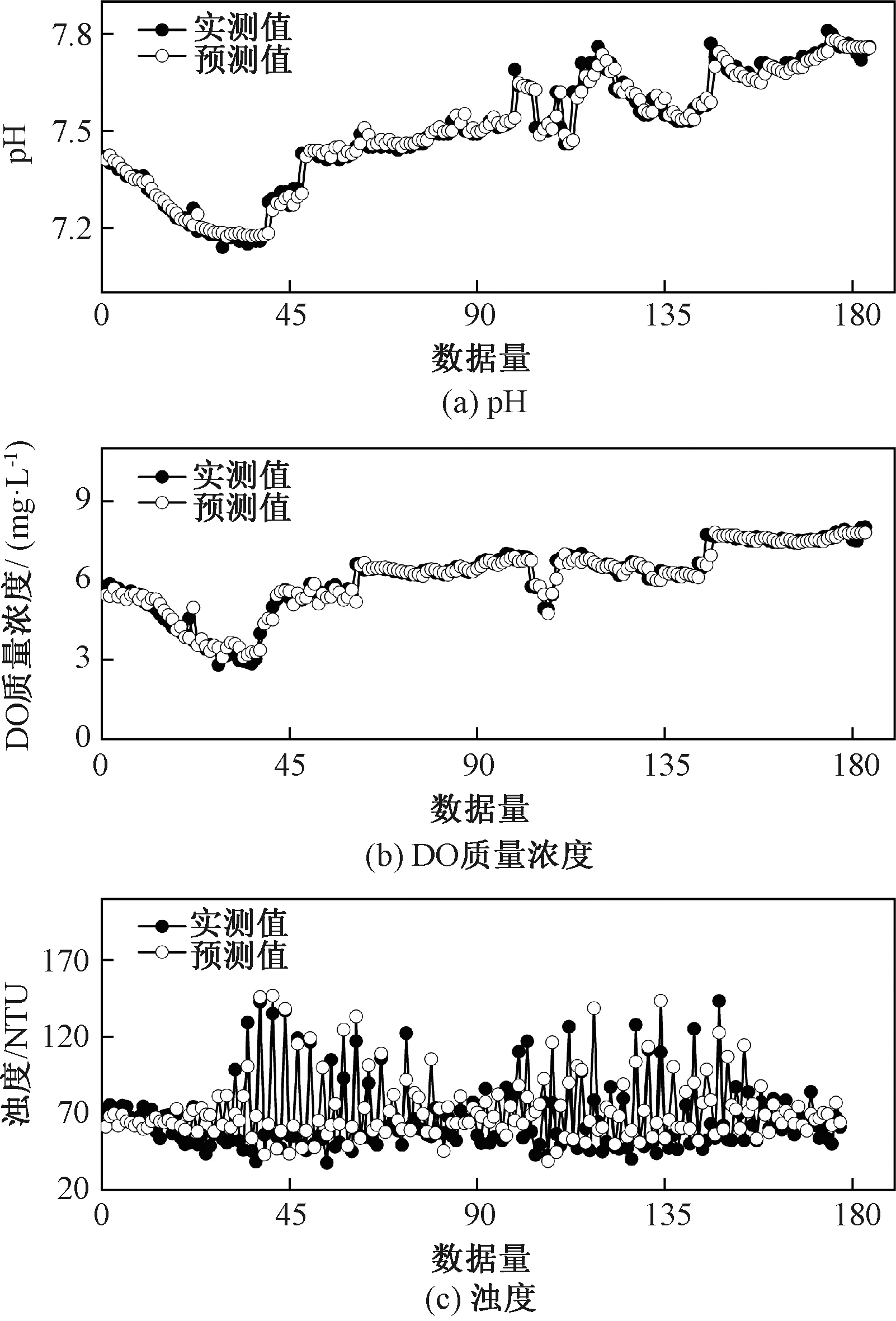
图7 预测模型对pH、DO质量浓度和浊度的预测效果Fig.7 Model prediction performance of pH, DO mass concentration and turbidity

由图7和表9可以看出，基于L-M算法建立的NAR神经网络模型对目标断面pH、DO质量浓度和浊度的预测值与实测值的变化趋势基本一致。结合RMSE值和MAPE值可知:输入数据段经优化选取和结构参数调整后，NAR神经网络模型的预测精度和自相关检验通过率均得到显著改善;各时间序列预测结果出现的差异主要是由原始时间序列波动和量级的影响所致。由实测结果可知，目标断面pH值在7.13～7.82波动，而DO质量浓度虽出现骤变情况，但骤变前后两个点的值很接近。相比之下，浊度易受往来船只和天气等因素的影响，即使剔除了异常数据，其数据波动(40～150 NTU)仍较大。由此可见，数据波动可能是造成pH、DO质量浓度和浊度预测结果具有差异性的主要原因。

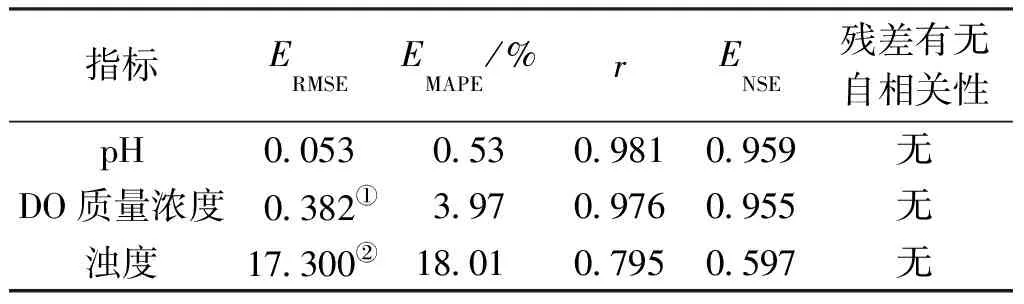
表9 预测效果评价Table 9 Evaluation of the prediction effect

3 结 论

(1)通过调整输入数据量、延迟阶数和隐含层神经元数优化NAR神经网络模型，当输入数据量为180，模型参数延迟阶数分别为2、3和9，隐含层神经元数为10时，模型对pH、DO质量浓度和浊度的预测效果最好。

(2)在最优参数设置条件下，NAR神经网络模型对pH、DO质量浓度和浊度的预测均方根误差分别为0.053、0.382 mg/L和17.300 NTU，平均绝对百分比误差分别为0.53%、3.97%和18.01%，模型对pH和DO质量浓度的预测精度优于浊度。

(3)针对地表水环境系统复杂且完全非线性的特点，NAR神经网络模型具有很强的非线性映射能力和灵活的网络结构，预测精度较高，在水质预测预警和评价方面具有较好的应用价值。