基于自适应t分布变异麻雀搜索算法的无人机航迹规划

李 楠， 薛建凯， 舒慧生

(东华大学 a. 信息科学与技术学院, b. 数字化纺织服装技术教育部工程研究中心,c. 理学院， 上海 201620)

无人机(unmanned aerial vehicles, UAVs) 由于具有可以使人类完全远离生命危险的巨大优势，被用于执行各种高风险的任务[1]。随着各类无人机的广泛使用,无人机的航迹规划问题得到了充分研究。航迹规划允许无人机根据任务要求和约束，自主计算起点至目标点的最佳路径。但在优化过程中，随着问题复杂度的增加，很难找到一种有效的规划方法。可见对无人机的三维航迹进行优化具有实际意义和挑战性。

在对无人机的路径进行优化的过程中，最大的技术难点是如何避开障碍物和威胁区域。因为大多数的无人机飞行事故主要是由撞上障碍物或被敌方击落而造成的。例如，在救援或地质勘探中，无人机在飞行过程中所遇到的树木、岩石甚至鸟类都极有可能干扰无人机的飞行甚至造成无人机坠毁。当无人机用于交通运输时，如何避开高楼大厦也是至关重要的。甚至在当今信息化战争中，无人机如何快速躲避敌人的雷达、导弹的威胁也具有重要研究意义。因此在环境建模中有必要考虑障碍物和威胁区域。

群智能优化算法已成为求解无人机航迹优化问题的常用方法。Sujit 等[2]提出一种基于粒子群优化(particle swarm optimization, PSO)的实时规划算法，并应用于多无人机航迹规划问题；Zhang等[3]提出一种基于蚁群优化(ant colony optimization, ACO)算法的无人机路径优化方法，并成功规划出有效的航迹路线。Chen等[4]针对无人机的三维路径规划问题，提出一种改进的狼群搜索(wolf pack search, WPS)算法，改进算法的性能优于原始算法和遗传算法(genetic algorithm, GA)。群智能优化算法具有易实现及扩展性好、参数少等特点，极大地满足了无人机在进行航迹优化时对算法的稳定性、实时性需求。

随着科学技术的发展，更多优化算法被提出。麻雀搜索算法(sparrow search algorithm, SSA)[5]具有参数少、收敛速度快、易实现等优点, 成功应用于多个领域。例如：Liu等[6]提出一种改进的SSA用以解决再生能源系统优化的问题；Zhu等[7]提出一种自适应SSA对质子交换膜燃料电池的模型进行参数优化识别，仿真结果表明所提算法具有较好的优化效果；Liu等[8]提出一种增强型 SSA 优化卷积神经网络，实现高效、稳定的脑肿瘤优化诊断；Yuan等[9]提出一种改进SSA来优化光伏微电网系统，得到了理想的效果；欧阳城添等[10]提出多策略改进SSA，成功应用于主动悬架控制优化问题。

综上所述，对SSA的研究大致分为3类：算法本身的改进；与其他算法的融合；算法的实际应用。本文重点关注第1类和第3类的研究，提出一种基于自适应t分布变异的SSA用以优化无人机的三维路径。

1 数学模型

1.1 无人机飞行环境建模

环境模型的建立是检验无人机是否可以完成预期规划效果的基础和前提，其中障碍物的出现会对算法的性能提出更高的要求。采用函数模拟法[11]对地貌特征进行模拟，其数学表达式如式 (1)所示。

(1)

式中：(x,y) 为点坐标；z为对应的高度。通过改变a,b,c,d,e,f,g这些常系数的数值可以得到不同的地貌特征，能满足不同环境的建模需求。在此基础上还需叠加山峰模型构建障碍物，山峰模型[12]表达式如式(2)所示。

(2)

式中：ho为基准地形，hi为第i座山峰的高度；(xoi,yoi) 为第i座山峰的中心坐标位置；ai和bi分别为第i座山峰沿x轴和y轴方向的坡度。联立式(1)和(2)得到式(3)。

Z(x,y)=max[z(x,y),h(x,y)]

(3)

最终得到如图1所示的地形效果图。

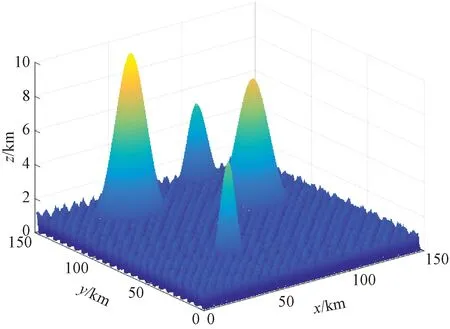
图1 地形仿真图Fig.1 The terrain simulation map

为了让无人机的飞行环境更加真实，在存在障碍物的前提下增加对无人机构成威胁的区域。威胁区域用半径为r的圆柱形表示，图2中的柱形体即是威胁区域。

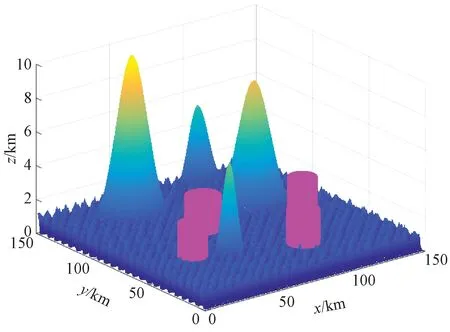
图2 威胁区域示意图Fig.2 Schematic diagram of threat area

1.2 无人机航迹规划建模

在无人机路径规划过程中，航路越短，飞行所需的时间和消耗的燃料越少。路径长度的计算公式如式(4)所示。

(4)

式中：g(i)和g(i+1)分别为第i个航路点和第i+1个航路点的坐标，记作(xi,yi,zi)，(xi+1,yi+1,zi+1)；li为第i个航路点和第i+1个航路点之间的距离；n为航路点个数；Lpath为路径长度函数。

合适的飞行高度对无人机航路规划具有重要影响。对于大多数类型的无人机而言，飞行高度的变化不能太频繁和剧烈。稳定的飞行高度可以节省很多燃料，安全指数更高。此外，当无人机在较低高度飞行时，其可利用周围地形进行自身掩盖，以此降低遇到未知危险的概率。飞行高度代价函数[4]定义如式(5)所示。

(5)

式中：hheight为飞行高度代价函数。

无人机的稳定性和可控性受转角代价的约束，并且在无人机路径规划过程中，转弯角度不应大于预先设定的最大转角[13]。转角代价函数的定义如式(6)所示。

(6)

式中：ai和ai+1为第i,i+1段航路段向量；|ai|和|ai+1|为ai和ai+1的长度；Ф为最大转角；δ为当前转角；Jturn为转角代价函数。

将无人机航路规划问题定义为一系列优化准则和约束条件。通过建立路径长度函数、飞行高度代价函数及转角代价函数，得到多目标代价评估函数，其表达式如下：

Jcost=w1Lpath+w2hheight+w3Jturn

(7)

式中：Jcost为总的代价函数；参数wi(i=1,2,3)需满足如下条件：

(8)

通过对总的代价评估函数进行优化，规划出一条路径。但是得到的路径很容易形成折线形导致无人机无法按规划路线飞行，需对这部分路线作平滑处理,因此采用B样条曲线对航路点进行平滑处理。B样条曲线表达式如下：

(9)

式中：m为节点ei的个数；ei的取值范围为{e0,e1,…,em-1}；Pi为控制节点；Ci,n(e)为n阶B样条基数，形式如下：

(10)

(11)

2 麻雀搜索算法

SSA主要是受麻雀群体觅食过程的启发而提出的，根据麻雀的觅食特点，其种群中的个体身份被分为发现者和加入者。麻雀种群中个体的身份(发现者或加入者)取决于自身的适应度值。对适应度值进行排序，其中适应度值较优的个体被认为是发现者。加入者在发现者周围获取食物，也可通过争夺获得食物。与此同时群体中的一些麻雀感知到危险后，也会进行相应位置的更新。研究[14]表明，麻雀能够在发现者和加入者两种身份中任意转换。

在SSA中，将待优化的函数视为食物，函数变量视为麻雀的位置。在d维解空间中发现者的位置更新描述如下：

(12)

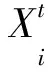
加入者的位置更新公式如下：

(13)

式中：Xp为所有发现者中最优麻雀个体的位置；Xworst为整个种群中麻雀个体最劣的位置；N为麻雀个体总数；A为1×d的矩阵，元素为1或-1，并且A+=AT(AAT)-1。

在SSA 中，麻雀种群在意识到危险时会表现出反捕食行为，其数学模型描述如下:

(14)

3 改进麻雀搜索算法

3.1 自适应t分布变异

t分布又称学生分布，其含有自由度参数m的概率密度函数为

(15)

t(m→∞)→N(0,1),t(m→1)=C(0,1)

(16)

式中：N(0,1)为高斯分布；C(0,1)为柯西分布。从式(16)中可以看出，高斯分布和柯西分布是t分布的两个边界特例分布[15]，三者的函数分布如图3所示。

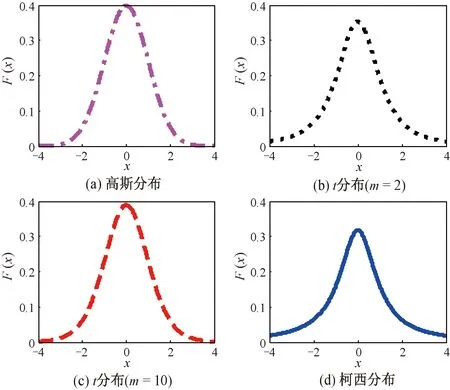
图3 高斯分布、t 分布和柯西分布密度函数Fig.3 Density functions of Gaussian distribution,t distribution, and Cauchy distribution

为进一步提高SSA的寻优性能以及防止在迭代后期算法陷入局部最优，对麻雀个体的位置采取如式(17)所示的自适应t分布变异策略。

(17)

式中：Xi*为变异后的麻雀位置；Xi为第i个麻雀个体的位置；t(M)是以SSA迭代次数为自由度的t分布。自适应t分布变异策略充分利用当前的种群信息。在迭代初期，迭代次数较小，t分布变异类似柯西分布变异，使得算法具有较强的全局探索能力；在迭代后期，迭代次数较大，t分布变异类似高斯分布变异，使得算法具有较好的局部开发能力。

3.2 改进麻雀搜索算法优化流程

基于改进SSA的无人机三维航迹优化流程如下：

(1)参数及种群初始化，如最大迭代次数、变异概率P、最大转角、无人机飞行区域大小的设置等。

(2)设置威胁区域中心的平面坐标、半径和无人机的起始点、目标点等。

(3)运用改进SSA对式(7)进行优化与更新，并对候选路径进行保存。

(4)更新发现者、加入者以及意识到危险的麻雀的位置。

(5)如果随机数rand小于给定的P值，根据式(17)对麻雀个体位置进行变异。

(6)更新路径。如果当前航路点优于之前，覆盖之前的航路点。

(7)判断终止条件。如果已满足预期要求则停止运行，否则，返回(3)继续执行。

(8)输出最佳路线。

4 试验仿真

4.1 试验环境及参数设置

为验证所提算法的有效性和可行性，同原始SSA和PSO算法进行比较。在MATLAB 2014a的试验环境下运行，电脑配置：3.40 GHz的英特尔i7处理器和4 GB内存。PSO、SSA以及改进SSA的种群大小均设置为50，最大迭代次数为200。SSA和改进SSA参数设置：安全阈值T=0.8，发现者的数量为10，变异概率P=0.5。PSO算法的参数设置为c1=c2=1.494 45，w=0.729。无人机的起点和终点坐标分别为(5, 100, 1.14)和(150, 50, 1.54)。最大转角Φ设置为90o，w1～w3分别设置为0.5、0.2、0.3。表1给出了威胁区域中心的平面坐标和半径。

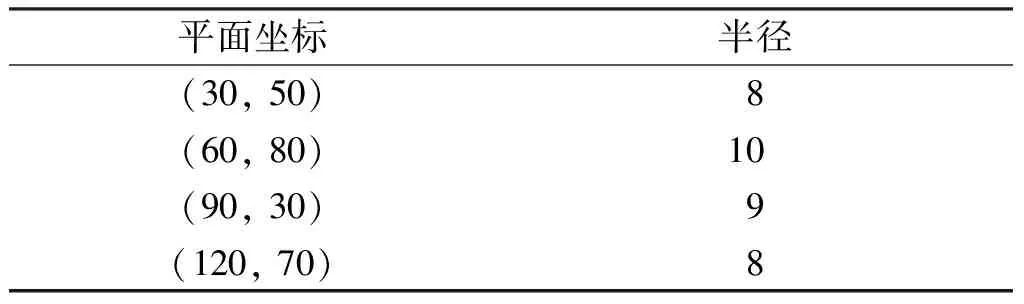
表1 威胁区域分布Table 1 The distribution of threat area km

4.2 测试与分析

图4～6分别给出了基于PSO算法、SSA和改进SSA的无人机三维航迹路线规划出的一条合理化路线。但是从图5可以看出，原始SSA在优化过程中陷入了局部最优而无法跳出，导致寻优精度降低。PSO算法在此类问题上也出现“早熟”现象，因而无法获取最优值。由此可见，PSO算法和原始SSA在搜索到整个种群的较优区域时，个体会逐步向当前最优解靠拢而发生聚集现象，最终导致整个群体陷入局部最优而无法找到全局最优解。

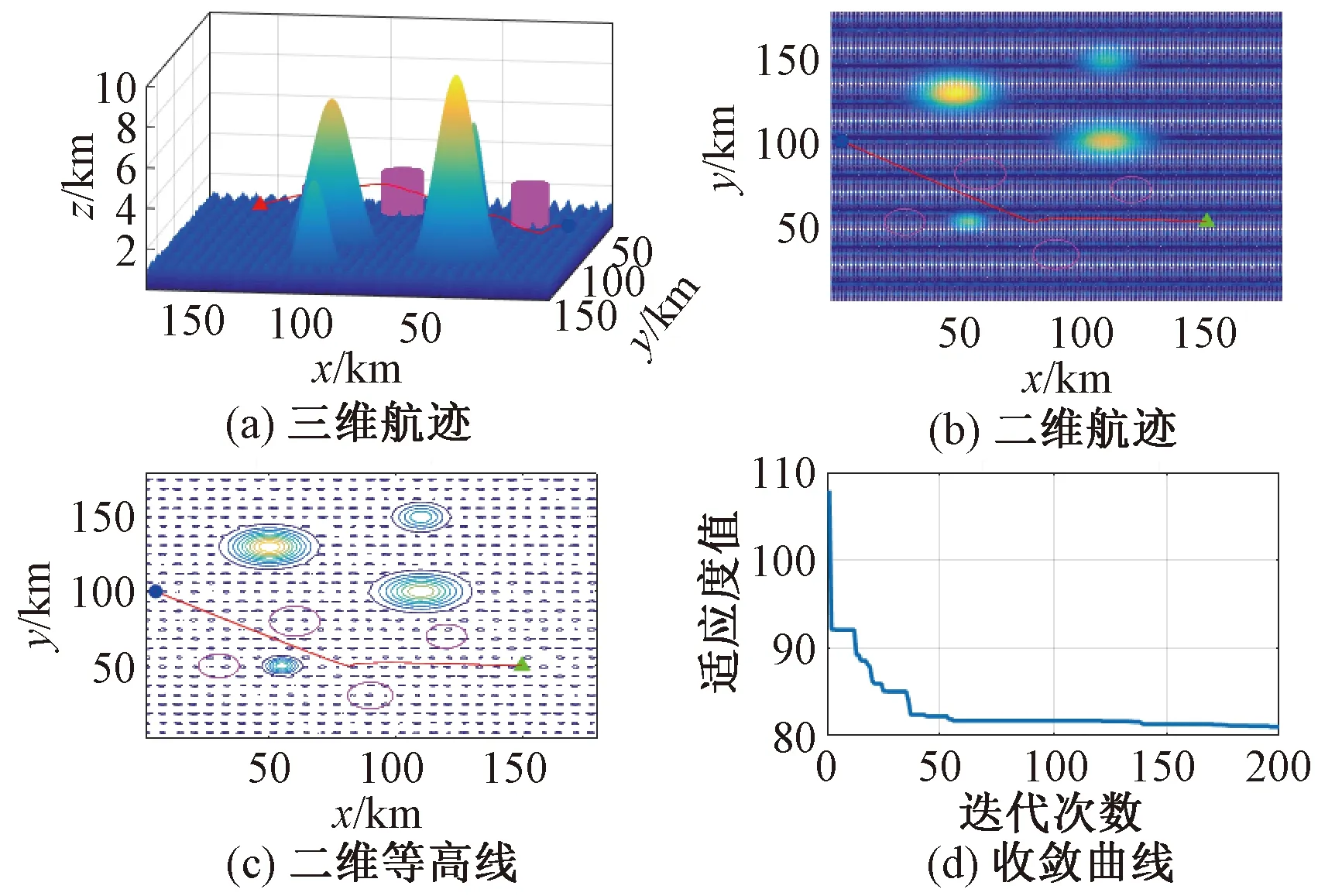
图4 基于PSO算法的最佳路线Fig.4 The best route based on PSO algorithm

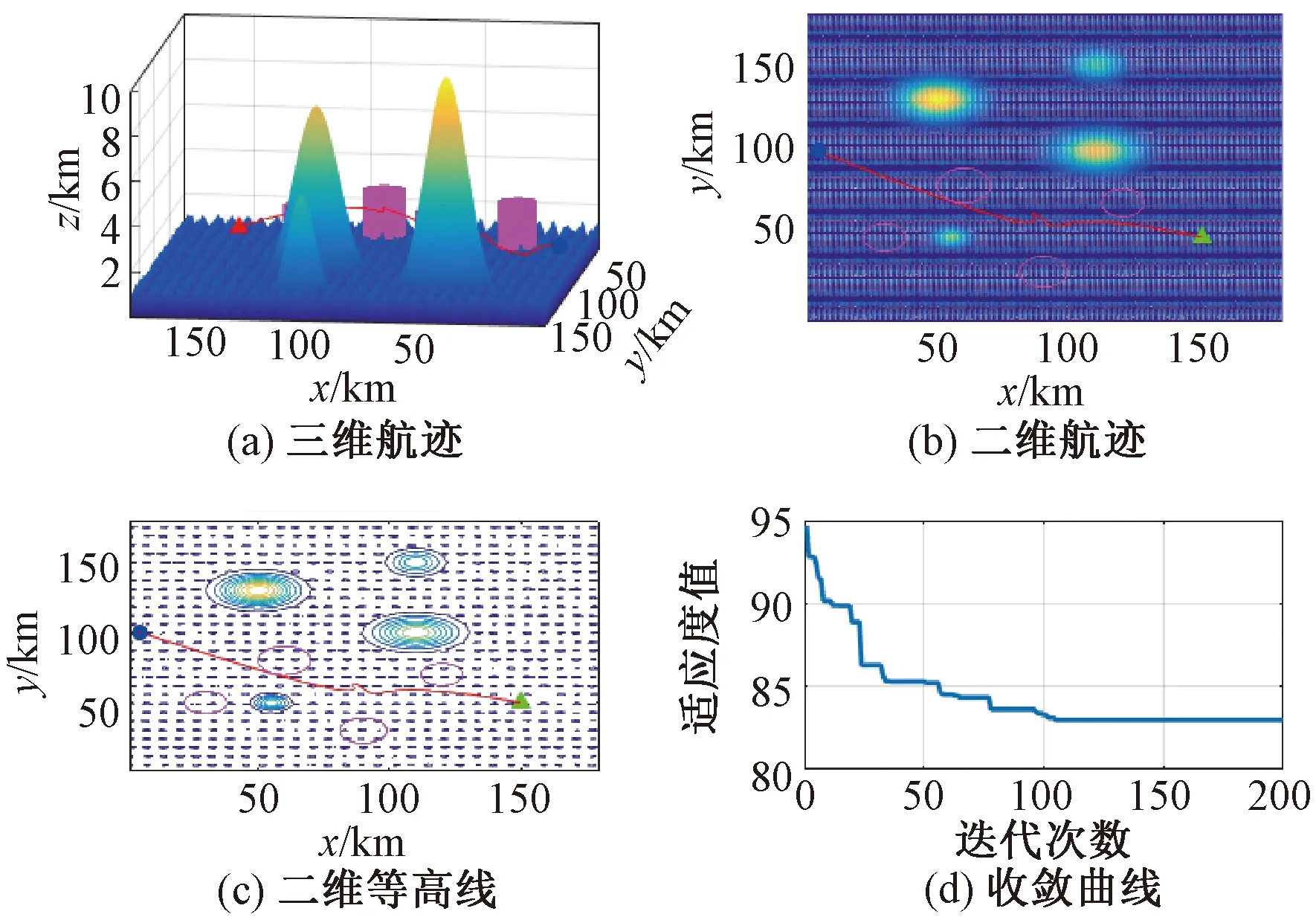
图5 基于SSA的最佳路线Fig.5 The best route based on SSA

图6 基于改进SSA的最佳路线Fig.6 The best route based on improved SSA

基于自适应t分布变异的SSA可以很好地平衡全局搜索和局部开发能力，增加了种群的多样性，寻优精度及收敛速度均得到了提高,由此可知，改进SSA求解的质量更高,收敛速度更快，能够有效缩短任务执行时间。总而言之，基于自适应t分布变异的SSA在无人机三维航迹优化问题上具有更好的性能。对算法生成的路径进行平滑处理，最终得到符合预期要求无人机飞行路线。

5 结 语

研究了无人机航迹规划问题，包括环境模型和航迹规划模型的构建,其目标是最小化多目标代价函数，包括航迹长度函数、飞行高度代价函数、转角代价函数。提出基于自适应t分布变异的SSA的优化方法，并同SSA和PSO算法进行了比较。仿真试验表明，与PSO算法和SSA相比,改进SSA在收敛速度、寻优精度方面均得到了提高。

后续研究中可在无人机建模中引入更多的约束和模型设计，如飞行速度约束、不同类型的环境约束和动态威胁等，也可将改进SSA进一步拓展到无人机的任务分配、编队控制等其他优化问题上。