一种EMTR与ewt结合的故障测距方法

刘 蕾 赵天玮 刘 通

（ 1.华北水利水电大学电力学院 郑州 450045； 2.东北大学 沈阳 110819）

引言

在全球经济迅速发展的浪潮下，电力作为国民经济的基础行业，不仅为人类的生产生活提供了保障，同时对于现代工业、农业、以及互联网等行业的发展不可或缺。输电线路作为电力运输的大动脉，为满足人们日益上涨的用电需求，线路跨度大、结构也趋于复杂，运行中的系统易受到输送环境等的影响，极大程度上增加线路发生故障的概率。为保证电力系统安全稳定的运行，快速、准确的故障定位能够大幅度提高电力系统的供电可靠性。

传统的输电线路故障测距方法大致可以分为两个大类[1]：(i)阻抗法，以及(ii)行波法。第一类是通过分析和计算线路故障时所测得的电压、电流，求出故障点的距离。该方法成本低廉且应用简单，但进行了太多的简化和假设，受到过渡电阻、分布式电源等的影响较大[2]。第二类行波法，根据所需观测点的数量进一步分类，即单端、两端和多端方法。行波法克服了阻抗法的一些缺陷，然而两端和多端观测点需要通信和时间的校准设备，以及存在着复杂的信号处理技术[3-5]。

电磁时间反转（Electromagnetic time reversal, EMTR）技术，是将收到的电磁波信号先进行时间序列上的一个反转处理，再将时间反转后的信号发射出去。该方法应用于输电线路的故障测距中，并且不受故障类型，过渡电阻以及运行方式的影响，可靠性较高[6]。

1 EMTR原理

1.1 EMTR在单一无损线路中原理

EMTR理论其基本思想是利用波动方程在时间上的可逆性，对所测得的信号在时间序列上进行反转。文献[7-9]将EMTR技术应用在输电线路故障定位中，结果表明，当在特定观察点观察到的电磁瞬变被时间反转并注回系统时，他们会收敛到故障位置。

式（1）中t是信号的持续时间，并添加了等于记录持续时间T的时间延迟。即

EMTR应用于频域中：

式中：

F*(,ω)是f= (,-t)的傅里叶变换。

利用图1所示的输电线路的分布参数模型，来证明行波在输电线路上的传输过程符合EMTR应用的前提条件。

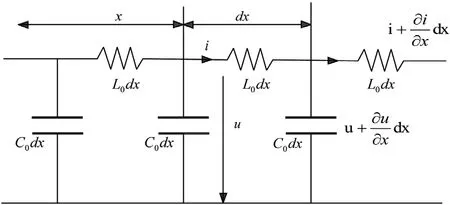
图1 分布式无损线路传播简图

无损传输线（其中R=0，G=0）的电压波动方程为

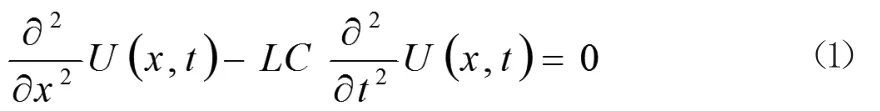
式中：

U(x,t)—相电压；

L、C—传输线的电感和电容参数。其时间反转方程为：

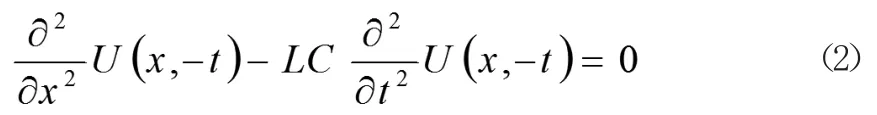
当U(x,t)是波动方程的一个解时，U(x,-t)也是方程的一个解。

由于电网传输线的纵向电阻值通常比较小，可以考虑EMTR对这种情况的适用性。

1.2 EMTR在输电线路的故障测距原理

将实际输电线路化简为一个简单双端供电系统模型，如图2所示为简单双端供电输电线故障简图。

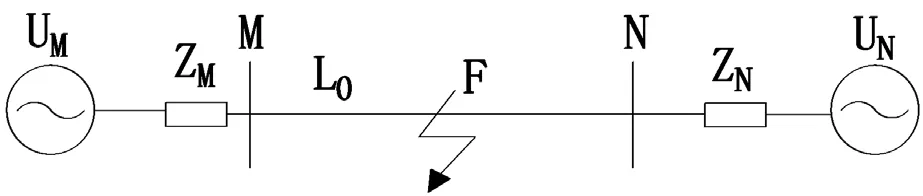
图2 简单双端供电输电线路故障模型

具体故障测距步骤如下：

1）线路的故障点设置为F，线路两侧故障录波器记录故障后的暂态电压、电流量，记为uM(t)和iM(t)、uN(t)和iN(t)。

设经过处理后电气量，线路两端电压、电流分量为UM与IM、UN与IN，M侧处的电流表达式为：

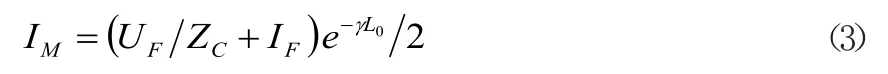
式中，

ZC—线路的波阻抗；

γ—线路的传播系数；

UF、IF—分别为线路故障处电压、电流。

在长度为L0线路中，上式频域中取共轭得到电流时间反转的结果如下：

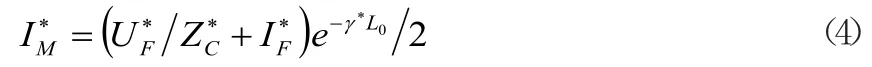
N侧电流同理。

2）建立镜像线路，忽略反射波。在线路M端将由信号发生器产生反演故障信号，注入到镜像线路中，设置n个假设故障点，利用下式可以求出在各假设故障点处的故障电流。

3）反转后的相电流注入镜像线路后，在实际故障点处会出现时空的同步聚焦，此时电流能量出现极大值点。取无损镜像线路中假设故障点电流最大值max{||}。

1.3 ewt算法

经验小波变换（ewt）算法为实现对原始信号的傅里叶频谱进行自适应的分割，利用原始信号频谱信息来求得所需带通滤波器的形式，构造出适应处理原始信号的带通滤波器[10,11]。将原始信号傅里叶频谱取值范围划分为[0,π]，信号频谱自适应划分为N个区。定义ωn为对应区间边界，对应频带为Λn。其划分的区间段可以表达为：

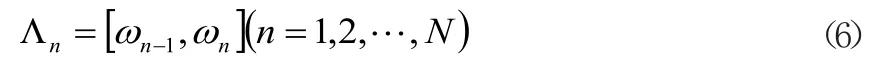
式中:

ω0=0；ωN=π。

各个区间的并集为[0,π]。定义每个频带的边界带宽为τn，称此以ωn为中心角频率。经验小波即定义在每个频带Λn上的窄带滤波器。在构造小波时，经验小波变换采用Meyer型正交小波基构建理论的来构造小波基函数，从而得出经验尺度函数n(ω)如下式所示：

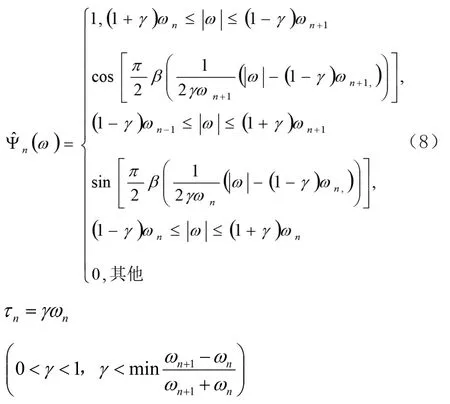
β(x)为x∈[0,1]内满足K阶导的任意函数。为简化计算，一般采用如下所示的表达式：

将傅里叶变换与逆变换分别记为F[·]和F-1[·]，经验小波变换的细节系数Wx(n,t)为信号xt与小波函数n(ω)的内积：

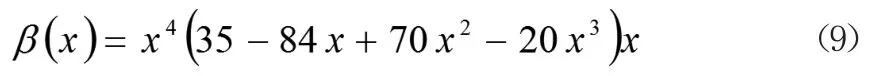
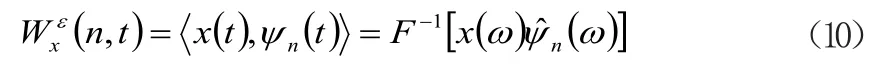
近似系数W0(n,t)为信号xt和经验尺度函数n(ω)的内积：

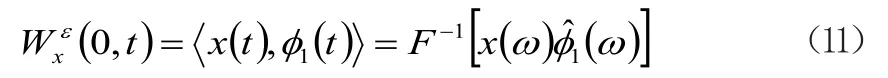
因此，重构信号xc(t)如下：

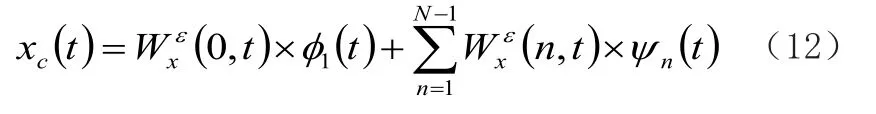
2 仿真与验证

在PSCAD中搭建如图3所示500 kV电力线路故障测距仿真模型，线路两侧设置三相交流供电系统，额定频率为50 Hz。

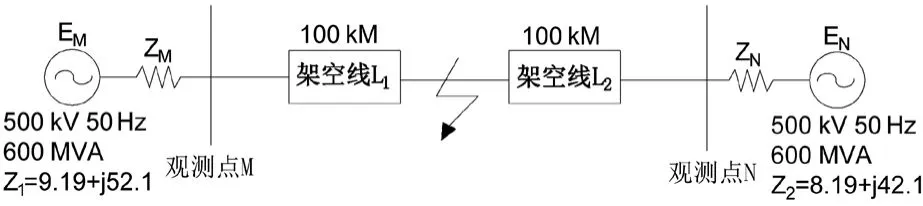
图3 PSCAD中搭建输电线模型

输电线路为三相分布的架空线L。线路总长度为200 km，其中架空线路采用LGJ-400/35的4分裂导线，正序电阻r1=0.018 47 Ω/km，零序电阻r0=0.163 7 Ω/km，正序感抗x1=0.276 1 Ω/km，零序感抗x0=1.152 44 Ω/km。

假设线路在0.2 s时刻发生金属性故障，仿真结果取从故障前一个周期到故障后一个周期，即1.98～2.02 s间。以A相单相接地故障为例，故障点设置在距离M端100 km处，在PSCAD中以M端观测点的暂态电气量为例。

将观测到的暂态电气量导入MATLAB中，使用ewt提取高频分量，并进行时间反转。

将反转后的高频分量注入镜像线路中，此时在故障点处电流出现极值点。

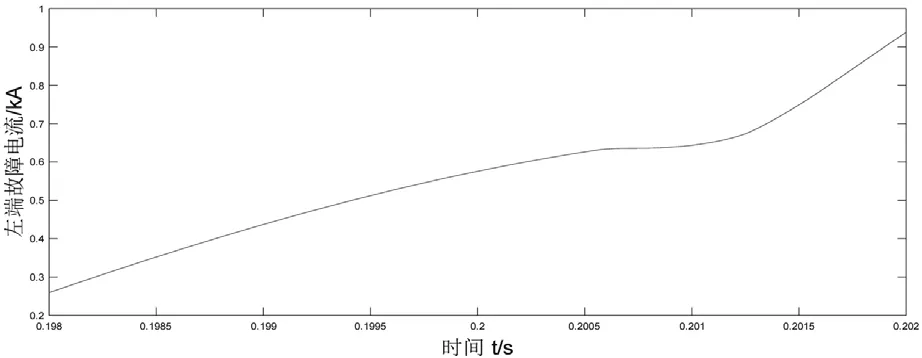
图4 M端电流暂态量

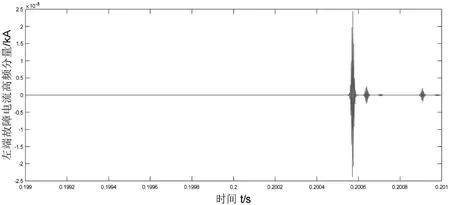
图5 M端相电流经经验小波变换后高频分量

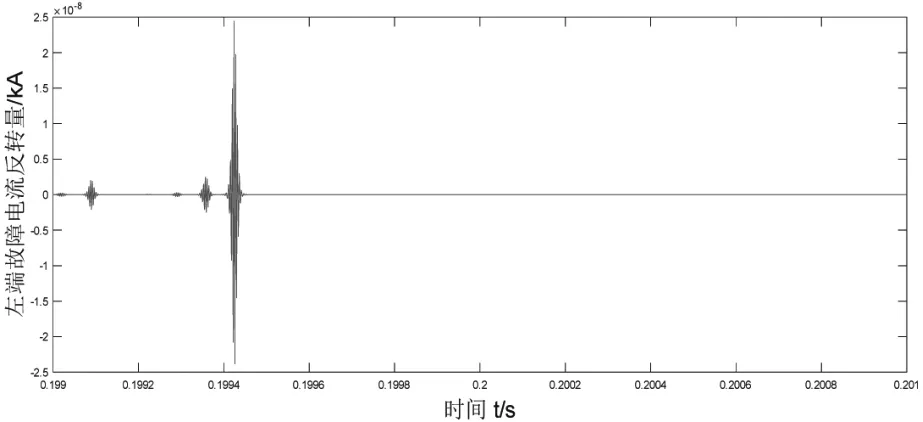
图6 M端相电流经时间反转后的高频分量

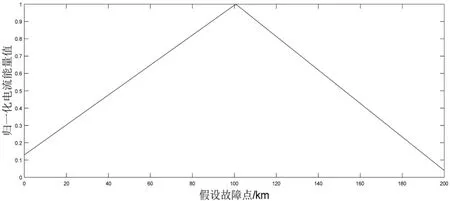
图7 故障测距结果

最终得到的测距结果为100.725 km，故障测距绝对误差为0.362 5 %。

3 结论

本文为将EMTR理论应用到输电线路故障测距中，验证了在无损线路具有时间上的可逆性，并将此方法运用到一段架空线中。通过上述的仿真结果可以得出该方法应用灵活，测距精度高。