基于数据驱动的重型燃气轮机多模融合建模方法研究

谭湘敏，李 伟，沈友昊，韩 博，孙嘉娴，陈士龙

(中国科学院工程热物理研究所 轻型动力重点实验室，北京 100190)

重型燃气轮机是典型的非线性多变量系统，其全工作流程建模具有较大的挑战性，而建模技术作为重型燃气轮机精准监测、故障诊断、控制优化和性能预测等工作的前提，其重要性不言而喻。因此，开展此项工作具有重要意义。

就已有工作而言，大体上可分为“白盒”模型、“黑盒”模型和“灰盒”模型。“白盒”模型的基本原理是根据燃气轮机遵循的布雷顿循环原理，按照各个部件的工作特性，求解流量连续方程、压力平衡方程、功率平衡方程等三类非线性平衡方程,建立燃气轮机共同工作模型[1-5]。“灰盒”模型介于“白盒”模型和“黑盒”模型两者之间，是一种数据和模型协同驱动的架构[6]，譬如：基于机理法得到模型的架构，再基于数据驱动的方法得到架构的具体参数。“黑盒”模型重点在于研究系统输入输出的关系，而忽略其内部的物理过程。常见的“黑盒”模型有模糊系统模型、人工神经网络模型[7-10]等，受益于近年来人工智能、大数据等领域的蓬勃发展，这类方法应用越来越广泛。文献[8]针对PG9351FA重型燃气轮机的起动过程，设计了基于非线性有源自回归(nonlinear autoregressive with external input, NARX)模型，结果表明其精度好且具有较好的泛化能力。文献[7]基于NARX模型，利用GE 9FA机组现场运行数据对燃气轮机的起动及加载动态过程进行了建模，取得了较好的效果。以上工作充分说明了采用NARX模型对重型燃气轮机进行建模是可行且效果良好的，因而本文采用数据驱动的“黑盒”模型来构建重型燃气轮机全工作过程的数学模型。

然而，在重型燃气轮机建模领域，目前数据驱动方法尚存在的主要问题有：①已有工作中多采用简化模型，带有强烈的假设，与实际情况差别较大，未考虑各个工作模式的输入输出的不同，实际上，燃气轮机在不同阶段工作机理迥异，导致模型的输入输出亦不尽相同，不能笼统为一个模型；②NARX模型所涉及的层数、节点数、传输函数、优化函数、延时阶数多根据经验选定，缺乏理论或实验准则指导，不容易得到闭环收敛的NARX模型；③未考虑数据采样周期和控制周期异步的问题。为解决上述问题，本文基于某电厂GE 9FA重型燃气轮机实际运行数据和数据驱动建模的基本思路，引入NARX模型和神经网络架构搜索(neural architecture search, NAS)方法，结合线性插值方法，采用多模融合的方案构建了该重型燃气轮机的模型，实现了燃气轮机全流程的高精度建模，并进行了分析说明。

1 问题描述

本节主要有两项工作：①基于某电厂GE 9FA重型燃气轮机实际运行数据完成整个工作过程的分段并确定工作模式，确定每种模式的输入向量和输出向量，为建模做准备；②确定重型燃气轮机完整工作过程数学模型的基本形式、实现方法和评价指标。

1.1 重型燃气轮机工作模式确定

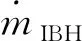
表1 重型燃气轮机的工作模式

1.2 各个模式的数学模型形式

本文建模的主要目的在于寻找以下非线性映射fi，具体形式可表示成差分方程形式。

yi(k)=fi[ui(k-1),ui(k-2),…,ui(k-nui),yi(k-1),yi(k-2),…,yi(k-nyi)]

(1)

式中：ui(i=1,2,3,4,5)和yi(i=1,2,3,4,5)分别为模型的输入向量和输出向量；nui和nyi分别为各个模式的输入和输出的延时阶数，代表模型的阶数。

由于神经网络中的NARX模型支持外部输入，具有很强的非线性映射能力，并具有自回归的动态特性，在时间序列建模和预测中应用广泛[9-10]，特别适合用于本文所提出建模问题的解决方案，因此本文采用NARX模型来实现重型燃气轮机完整工作过程的模型构建。评价指标采用平均相对误差(average absolute relative error, AARE)eAARE和均方根误差(root mean square error, RMSE)eRMSE，具体为：

(2)

(3)

2 多模融合建模方法

为解决上述建模问题，本节主要包括三方面内容：①基于NARX模型的多模融合建模规划；②基于神经网络架构搜索(NAS)方法，确定各段网络架构参数(神经元数量、传输函数和延时步数)、网络训练算法；③采用线性插值的方法解决数据采样周期和控制周期异步的问题。

2.1 基于NARX模型的多模融合建模规划

参照表1所示，在建模规划之前，须要完成数据整理。本文基于某电厂GE 9FA重型燃气轮机的实际运行数据开展工作，该数据中包含夏季起动、夏季升负荷、冬季升负荷、夏季降负荷和冬季降负荷等数据。本文主要以夏季起动、夏季升负荷、夏季降负荷运行数据来构建建模数据集，根据建模需要对数据进行分析，完成清洗和结构化工作。对于模式S1、S2(7输入4输出)采用4个NARX网络对4个输出进行建模，对于模式S3、S4(6输入4输出)控制量中少了一个(起动电机功率输入)，也采用4个NARX网络对4个输出进行建模，S5阶段(6输入5输出)则采用5个NARX网络对5个输出进行建模，整个多模融合模型包括21个神经网络，具体规划如图1所示。

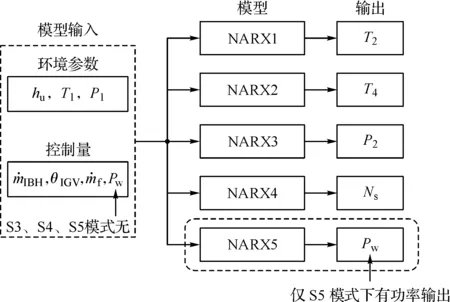
图1 多模融合建模规划

在建模过程中，NARX模型有三种工作模式，第一种是全开环模式(图2上所示)，第二种是全闭环模式(图2中所示)，第三种是半闭环模式(图2下所示)。本文所述的21个NARX模型均采用图2所示结构，在训练阶段采用开环模式，作为预测模型、参数解析模型或控制系统模型时主要工作在闭环模式或半闭环模式。此文中半闭环模式系指在运行过程中周期或非周期用真实输出作为NARX模型的输入来修正模型预测输出，可改善模型的收敛性。

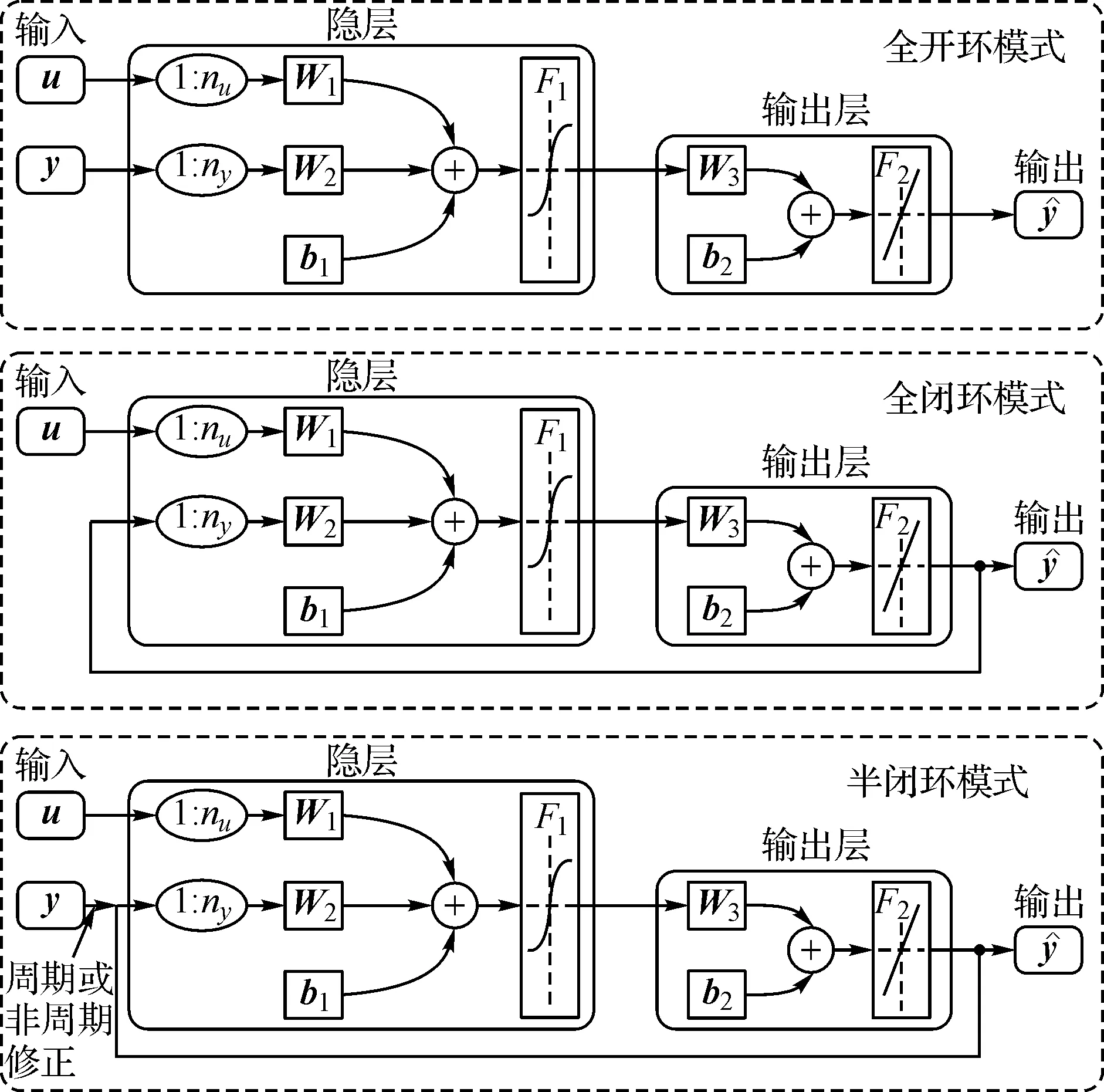
图2 NARX模型的三种模式

NARX模型可用公式表达如下：

y(k)=F2[W3·F1(W1·ud+W2·yd+b1)+b2]

(4)

式中：W1、W2、W3为权重矩阵；b1和b2分别是隐层和输出层的偏移向量；F1、F2分别是由隐层和输出层的传输函数确定的映射；ud表示输入延迟序列；yd为状态(输出)延迟序列。具体形式为：

ud=[uT(k-1),uT(k-2),…,uT(k-nu)]T

(5)

yd=[yT(k-1),yT(k-2),…,yT(k-ny)]T

(6)

在实践中，F1常选为tansig、logsig、elliotsig、radbas形式，F2常选为purelin形式，即f(x)=x。当F2选为purelin时，式(4)可以化简为

y(k)=W3·P+b2

(7)

式中：P=F1(W1·ud+W2·yd+b1)。

2.2 神经网络架构搜索方法

对于给定数据集和图2所示结构的NARX模型，其网络结构的具体参数(隐含层神经元个数、隐层传输函数、延时阶数、训练函数、输出层传输函数等)选择对模型性能影响较大，为此，本文采用了一种神经网络架构搜索(NAS)方法。具体思路如图3(N-S图)所示，首先需要根据建模要求获得必备数据集，并将数据集按照训练集、测试集划分；确定神经网络模型基本形式，本文固定为NARX模型；选择神经网络训练函数、隐含层神经元数、延时阶数、隐含层和输出层的传输函数；训练神经网络；训练完毕后测试神经网络，记录以此网络确定的模型的性能指标。循环执行图3中①至⑧步骤，直至设定范围搜索完毕。最后，按照性能指标(文中为eAARE)排序，确定最优网络的参数。考虑到训练中的不确定性因素的影响，可以重复做几次取较好性能的网络。

图3 神经网络架构搜索方法

2.3 数据采样周期与控制周期异步问题解决方法

在实践中，出于商业秘密或其他各种原因，原始数据的采样周期Ts可能和系统的控制周期Tc不一致，譬如：文中Ts为1.28 s，Tc为0.04 s。由于模型可能用到控制设计中，必须解决这个问题。本文假设在Ts周期范围内，控制量输入保持不变(零阶保持器)，输出量按照如下方式插值：

(8)

式中：i∈[1，R]，R为Ts/Tc向下取整值。

3 验证与分析

针对某电厂GE 9FA重型燃气轮机，以夏季起动、夏季升负荷、夏季降负荷实际运行数据来构建建模数据集。本节通过计算方式对模型的正确性和算法的有效性进行验证，验证计算机系统的配置为：①CPU：Intel Core i5-8300H；②内存：8GB DDR3；③操作系统：Windows10 64位操作系统，模型运行在MATLAB环境(版本为R2020a)。

根据上文2.1所述完成数据整理，原数据中包括500多项数据项，面向建模的实际需求，优选出11项数据作为模型的输入、输出和状态，整理好的数据集的基本情况如表2所示，数据的采样周期为1.28 s、控制周期为0.04 s。值得注意的是，起动电机功率数值为负时表明电网向电机输入功率，起动电机的工作在电动机模式，带动燃机轴旋转。表3为输入信号范围，要求模型使用过程中尽量要在此范围内进行。

表3 输入信号范围

基于上述2.2节中所述的神经网络架构搜索方法，搜索范围为：网络训练函数从traincgp、trainlm、traincgb、traincgf、trainbfg、trainscg、trainrp、trainoss、traingda、traingdx、traingdm、traingd中选择(共12种)，隐层神经网络节点数nH∈[10,20]，隐层传输函数从elliotsig、logsig、radbas、tansig中选择(共4种)，延时阶数nd∈[1,5]，输出层传输函数固定为purelin，完成一次搜索需要对2 640个不同结构的NARX网络进行训练。本文经过10次完整搜索后，综合考虑精度、易行性、实时性以及NARX模型闭环模式的收敛性来选择网络结构参数，各段优选的网络结构参数如表4所示。对于模式S1、S2、S3、S4，表4中的“隐层节点数”列对应于图1中NARX1至NARX4中4个网络的隐层节点数。譬如模式S1中的“12121212”表示NARX1至NARX4四个网络的隐层节点数均为12个；而对于模式S5，“1520101510”则表示NARX1至NARX5中5个网络的隐层节点数分别为15个、20个、10个、15个和10个。

表4 各段网络结构参数

基于多模融合方法得到的模型仿真效果如图4至图9所示，图10为控制量输入和整个工作过程的环境参数变化情况。下列图中“全开环”系指NARX模型的输入量y均为实测值(图2上)；“半闭环”系指在运行过程中可间隔一段时间用真实输出作为NARX模型的输入，本文每60 s修正一次(图2下)；“全闭环”的输入全部为模型的计算输出(图2中)。分析如下：

(a ) 控制量

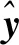
表5 模型精度

(2) 表6表明，尽管所提出的多模融合建模方法是基于神经网络的，但其计算复杂性完全可以接受，即使在普通的计算机系统上，模型迭代的平均时间约为0.4 ms，远远小于燃气轮机控制系统的控制周期(40 ms)。

表6 时间性能指标

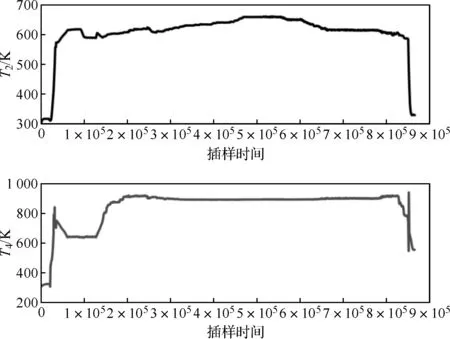
图9 插值后的T2、T4、P2和Ns

(4) 观察图4、图5、图6、图7、图8左图中的陡峭变化段，模型对于输入的突变能够快速反应，充分说明了模型具有较好的动态性能。

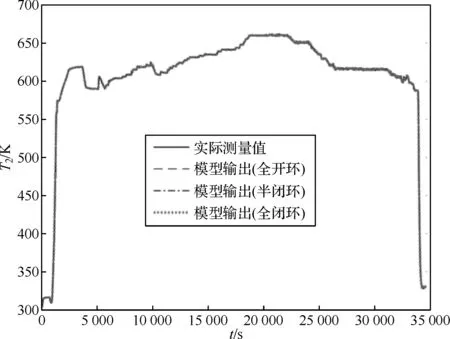
图4 压气机出口温度T2及相对误差

图5 透平排气温度T4及相对误差

图6 压气机出口压力P2及相对误差

图7 燃气轮机转速Ns及相对误差

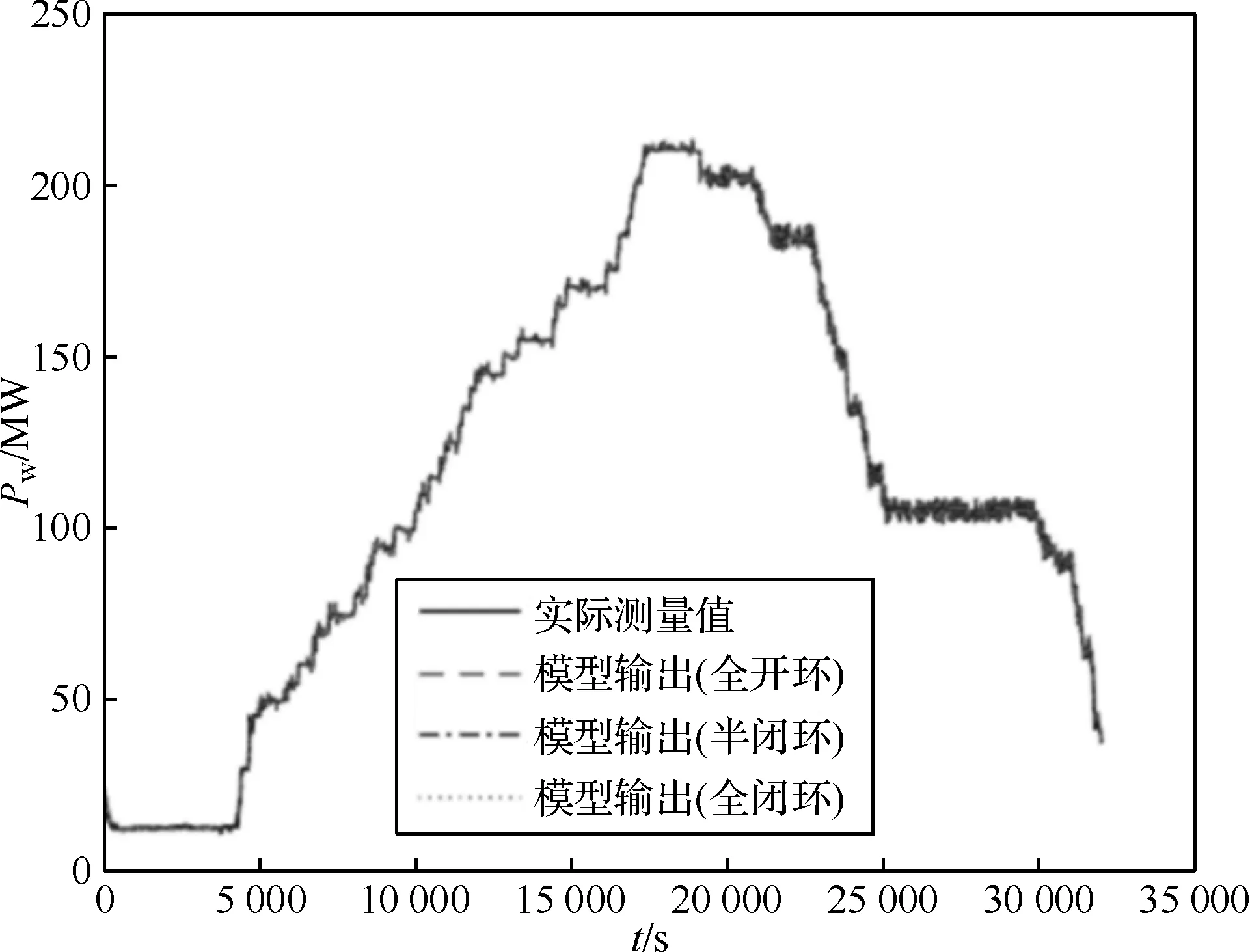
图8 输出功率Pw及相对误差

4 结论

针对重型燃气轮机高精度建模的问题，本文基于某电厂GE 9FA重型燃气轮机实际运行数据和数据驱动建模的基本思路，通过对其完整工作过程中的不同阶段进行分析，共分为五个阶段，分别对应于五种工作模式,引入NARX模型和神经网络架构搜索(NAS)方法，并结合线性插值方法，采用多模融合的方法构建了该型重型燃气轮机的数学模型，实现了燃气轮机全流程的高精度建模。仿真结果说明：

(1) 文中所提出基于数据驱动的多模融合建模方法能够满足重型燃气轮机完整工作过程建模的需求，采用这种方法所构建的全流程模型具有精度高、实时性好、动态性能优良的特点，能够应用于参数解析、性能预测、故障诊断和控制设计中。

(2) 文中所采用的NAS方法能准确搜索到性能优良的网络参数，快速完成模型构建工作。

(3) 所给出的线性插值方法，可产生大量数据用于控制设计或多粒度预测中，能够解决数据采样周期和控制周期异步的问题。

表5(续)