基于机理数据协同驱动的重型燃气轮机控制系统参数解析余度构建研究
孙嘉娴,谢振伟,谭湘敏,胡春艳,李 伟
(1. 中国科学院工程热物理研究所 轻型动力重点实验室,北京 100190;2. 中国科学院大学,北京 100190;3. 滨州学院 山东省航空材料与器件工程技术研究中心,山东 滨州 256600;4. 中国科学院 轻型动力创新研究院,北京 100190)
传感器解析余度技术能够降低控制系统的复杂性、减轻硬件重量、减少硬件体积和研制成本而备受关注。传感器解析余度研究是传感器容错控制研究的重要基础[1-2],是未来控制系统智能化发展的方向之一。目前,GE公司的MARK控制系统已经具备了训练传感器模型的功能,但具体技术对外界严格保密。我国正在推进重型燃气轮机自主设计,因此非常有必要开展解析余度构建方法研究,形成具备自主知识产权的重型燃气轮机控制系统传感器解析余度构建方法。
就目前已有工作而言,构建传感器解析余度的方法主要有机理分析法和数据驱动法。机理分析法是指通过对燃气轮机的工作机理进行深入分析,建立燃气轮机各参数之间的热力学公式作为某参数的解析余度。在确定的大气条件下,单轴燃气轮机的所有工况参数都是两个独立变量的函数,西门子燃气轮机控制系统就是通过压气机出口压力和透平排气温度建立起了燃气轮机功率的计算式[3];赵琳等[4]针对涡扇发动机的透平监视温度,提出了两种解析方法,分别是基于透平排气总温的解析方法和基于空气流量模型的解析方法,为透平监视温度建立了解析公式;张荣等[5]采用拟合加补偿的方式对航空发动机转速信号进行了重构,补偿方式是通过分析发动机原理来设计补偿环节。近年来,随着人工智能技术的发展,以神经网络为代表的机器学习算法应用于传感器解析余度的构建中,各种神经网络如BP、RBF、广义回归、支持向量机、NARX、极限学习机等得到了广泛研究[6-9]。针对神经网络解析余度设计的精度和实时性问题,人们也提出了对神经网络训练算法的改进方式[10-11]。
燃气轮机具有很强的非线性,状态参量间的关系极其复杂,采用机理分析法构建解析余度时只能做大量假设以简化计算,这会导致解析精度的降低,因而机理分析法具有一定的局限性。数据驱动法如神经网络,直接基于数据进行解析模型训练,而不必知道参数间的具体数学关系,简化了建模。但是,重型燃气轮机参数间的映射关系非常复杂,这给神经网络训练带来了一定难度,要想得到好的训练结果是不易的,须要花费大量的精力对神经网络进行改进。
基于上述考虑,本文采用机理分析与数据驱动结合的方式构建传感器参数的解析余度,称为机理数据协同驱动法。该方法结合了机理分析法和数据驱动法各自的优势,且思路清晰简单,易于实现,精度较高,并以压气机出口压力和压气机出口温度为例对所提方法进行了仿真验证。
1 方法原理
机理数据协同驱动法具体包括三步,如图1所示。首先分析重型燃气轮机工作机理,得到想要解析的参数与其他参数在典型工况下的热力学关系;然后采集重型燃气轮机实际的运行数据,输入至热力学关系式,将输出与实际数据比较得到误差样本数据,通过前馈神经网络训练误差样本数据,得到数据驱动模型,将该数据驱动模型作为热力学关系式的补偿部分。该方法的主要工作在于建立机理模型和数据驱动模型,其中数据驱动模型是影响解析精度的关键所在。
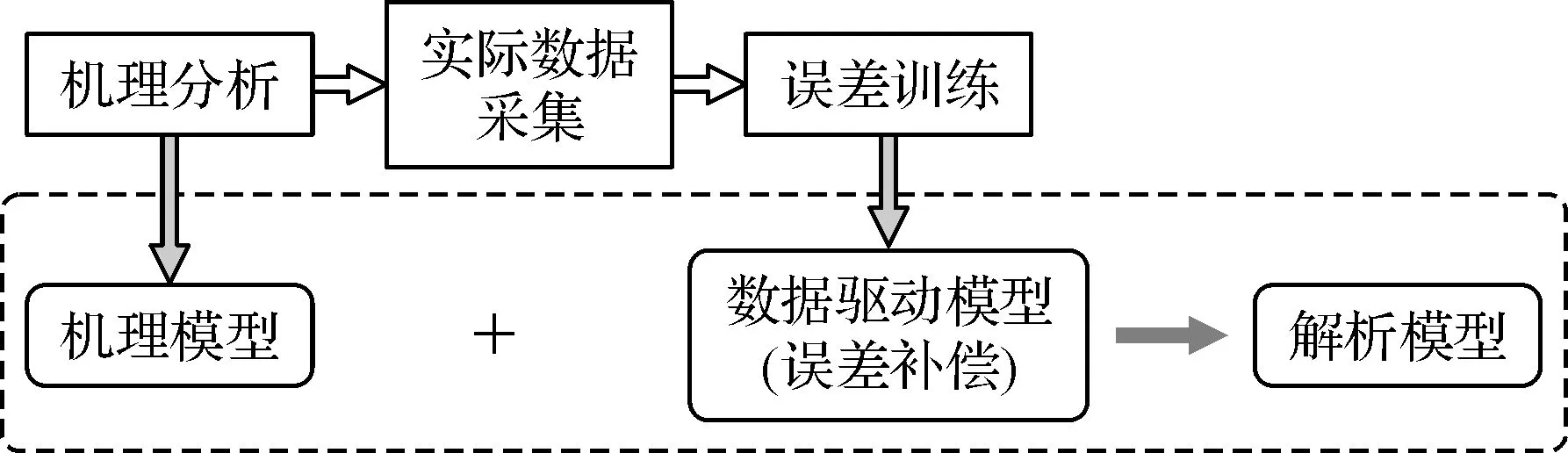
图1 传感器参数解析余度构建
1.1 机理模型的建立
燃气轮机核心部件包括压气机、燃烧室、透平,工质在核心部件的热力循环属于实际布雷顿循环过程。图2为布雷顿循环燃气轮机的工作原理,图3为燃气轮机实际布雷顿循环的p-v(压-容)图和T-s(温-熵)图。图中虚线表示理想布雷顿循环过程。忽略压力损失,实际布雷顿循环可分为四个过程:1-2为压气机中的不可逆绝热压缩过程;2-3为燃烧室中的等压加热过程;3- 4为透平中的不可逆绝热膨胀过程;4-1为排入大气时的等压放热过程。
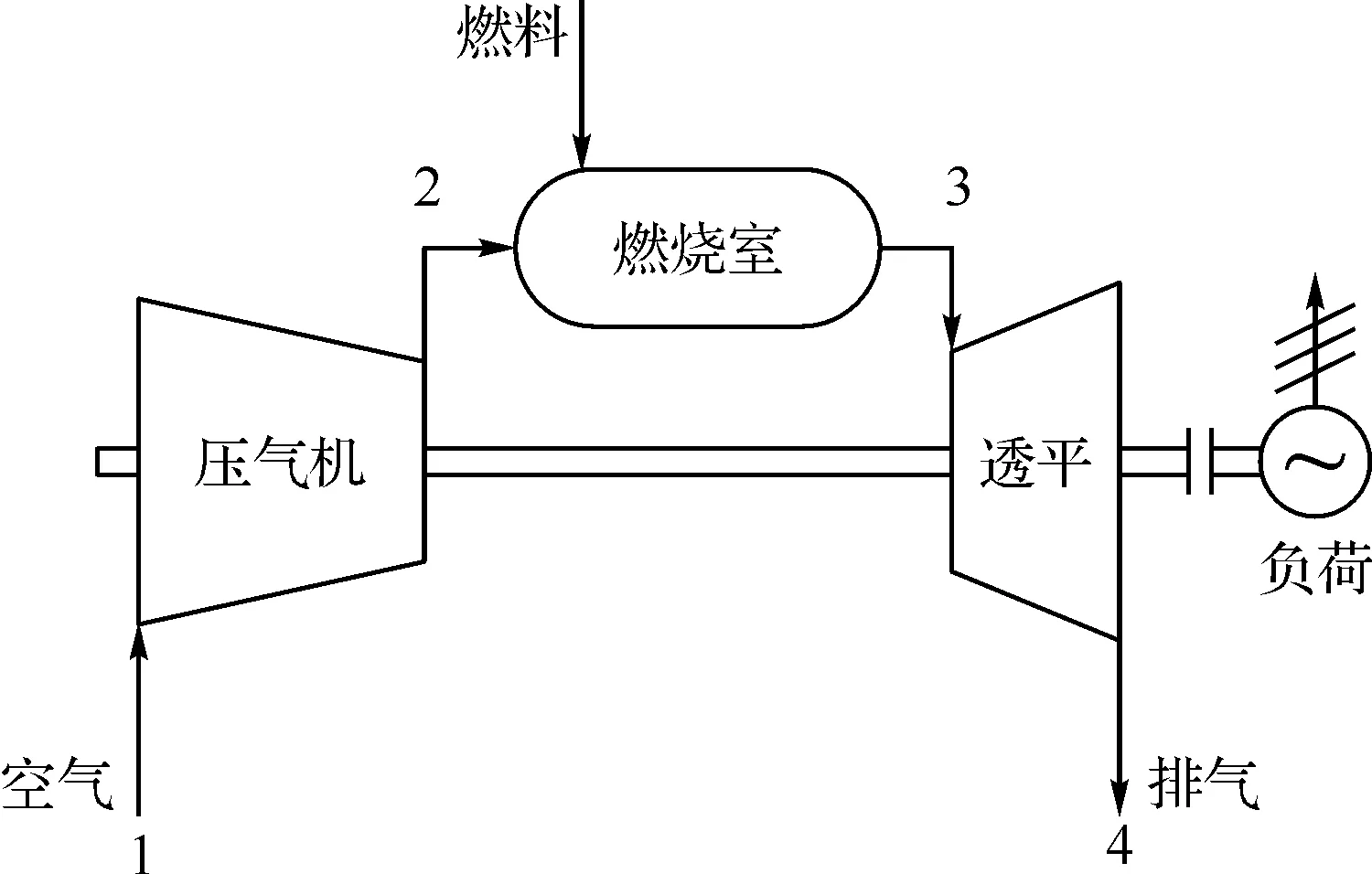
图2 布雷顿循环燃气轮机的工作原理[12]

图3 燃气轮机实际布雷顿循环的p-v(压-容)图和T-s(温-熵)图[12]
1-2表示压气机工作过程。由于机械摩擦、热扩散、扰动等不可逆因素的影响, 1-2过程为非等熵过程,压气机实际耗功大于工质的焓增量,则压气机效率ηc可表示为[13]:
(1)
式中:h1为工质在压气机进口的焓值,J/kg;h2s为工质在压气机出口的理想焓值,J/kg;h2为工质在压气机出口的实际焓值, J/kg;T1为工质在压气机进口的温度,K;T2s为工质在压气机出口的理想温度,K;T2为工质在压气机出口的实际温度, K。
根据等熵压缩过程中温度和压力的关系,可得:
(2)
式中:p1为工质在压气机进口的压力,Pa;p2为工质在压气机出口的压力,Pa;k为空气的比热比。
联立式(1)、式(2),可得到压气机出口压力和出口温度的热力学关系式:
(3)
(4)
同理,对于透平,其工作过程(即3- 4)与压气机正好相反,也可推出相应的进出口参数的热力学关系式:
(5)
(6)
式中:p3为透平进口压力,Pa;p4为透平出口压力,Pa;T3为透平进口温度,K;T4为透平出口温度, K;ηt为透平效率;kg为工质即燃气的比热比。
为简化计算,式(3)~式(6)中的效率、比热比可取典型工况下的定值,由此得到机理模型。实际上,由于环境条件、工质成分的变化[14]等因素,效率、比热比不可能为定值,这种简化会给机理模型引入误差。
1.2 数据驱动模型的建立
采用前馈神经网络建立数据驱动模型。由于燃气轮机的复杂性,误差采用常规的多项式拟合会导致精度难以提高,且多项式有高阶数值稳定性的问题,而前馈神经网络具有强大的非线性拟合能力,网络结构简单,如图4所示。相关研究表明,只要选择了合适的隐含层神经元数目,任何连续函数的多维非线性映射都可以由一个两层的前馈神经网络逼近[15]。对于给定的训练样本集D={(U,Y)|U∈Rq×n,Y∈Rn},其中U为输入向量,Y为输出向量,这里表示机理模型输出与实际测量数据间的误差,即:
Y=Yr-Ym
(7)
式中:Yr为实际测量数据;Ym为机理模型的输出数据。它们都为数据向量。由图4所示的神经网络,可得出误差估计为:

图4 前馈神经网络结构
(8)
训练神经网络权值和偏置,使如下的目标函数值达到最小[16]。
(9)
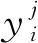
重型燃气轮机从开始工作到停机历经盘车、清吹、共同加速、独立加速、全速空载、负荷调整、停机共7个过程,主要的运行状态有三个:起动状态、全速空载状态和负荷调整状态,在不同运行状态下重型燃气轮机的控制方式不同。为了加快神经网络训练的收敛速度,提高最终数据驱动模型的精度,考虑在不同运行状态下优选神经网络输入参数,对神经网络进行分段训练。
控制燃气轮机最为重要的参数是压气机进口导叶角度(θ)和燃料流量(Wf),燃气轮机状态参量的变化是二者共同作用的结果,因此使用θ与Wf之比作为神经网络的输入参数之一,该参数反映了两个控制参数所包含的信息。起动过程中,反映燃气轮机状态的最主要的状态参量为燃气轮机转速(N),因此在起动阶段,N可作为神经网络的另一输入参数。起动状态下,神经网络输入为U=[θ/Wf,N/N0],其中N0为额定转速。
当转速到达额定转速后便保持不变,控制系统通过调节θ和Wf保证燃气轮机的正常工作,此时最能够反应燃气轮机状态的状态参量包括温度T和压力p。因此,在全速空载状态和负荷调整状态下,对于压气机出口压力的解析,神经网络输入为U=[θ/Wf,T2/T1];对于压气机出口温度的解析,神经网络输入为U=[θ/Wf,p2/p1]。神经网络训练的输入参数规划如图5所示。
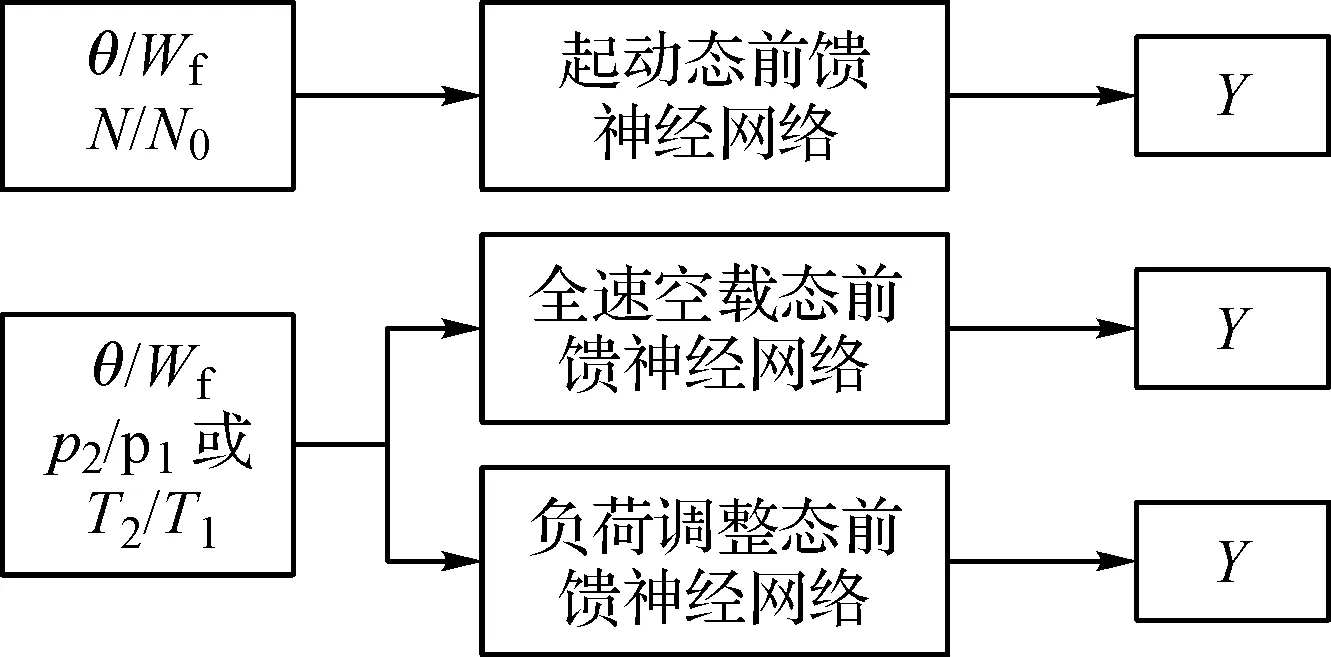
图5 神经网络训练输入参数优选
神经网络隐含层神经元数量不同、训练算法不同,网络的性能就会大不相同。对于不同阶段的数据集,为了获得相应的性能最佳的神经网络,需要对不同的网络结构进行性能评估,通常使用经验法或试错法[9-10],但会耗费大量时间,因此建立自动网络架构搜索程序,自动搜索出适用于某一数据集的最优神经网络结构。程序输入为:训练函数组、隐含层传递函数组、隐含层神经元最大个数a、训练数据集D;输出为:神经网络、验证集最佳性能、测试集最佳性能。采用穷举方式依次搜索并验证。
神经网络的性能评价指标采用均方误差(mean square error,MSE),具体为:
(10)

在实现尾水资源化利用的基础上,确定尾水导流系统的导流量。合理安排南水北调运行期、灌溉期、汛期不同时期的工程导流量。在南水北调调水期、非降雨时,可以在保证尾水导流工程正常运行的情况下,尾水通过导流系统进行导流;在降雨期、尾水导流工程满负荷运行及尾水无法导入时,则利用河道进行调蓄,尽可能减少尾水外导量。
搜索完毕后,按均方误差从小到大的顺序对所有神经网络排序。考虑神经网络的泛化能力,在训练集均方误差较小的情况下,选择测试集均方误差最小的网络进行训练,得到数据驱动模型。
由式(3)和式(8)、式(4)和式(8)可得压气机出口压力和压气机出口温度的解析模型:
(11)
(12)
式中:f、W、b的第一个下标代表解析的参数类型,第二个下标代表第几层神经网络。
解析模型的性能评价指标采用平均相对误差(average absolute relative error,AARE),具体为:
(13)

2 参数解析方法验证
本节以压气机出口压力和压气机出口温度为例,对机理数据协同驱动法进行仿真验证。
对于压气机出口压力的解析,机理模型采用公式(3),对于压气机出口温度的解析,机理模型采用公式(4);式中压气机效率取0.9,空气比热比取1.4。根据1.2节所述,将燃气轮机从点火到最后断网这个过程的输入参数数据输入至机理模型,得到误差数据,然后将误差数据分为三段,分别对应起动状态、全速空载状态和负荷调整状态;将每一个运行状态下的数据集划分为样本数据和验证数据,二者各占50%,样本数据用于网络架构搜索和数据驱动模型的训练,验证数据用于对参数解析方法的验证。
对每一段样本数据进行网络架构搜索,其中由于全速空载段的数据量很少,且全速空载段数据驱动模型输入参数的选择与负荷调整段一致,采用负荷调整段的搜索结果来表征全速空载段。搜索过程中为提高神经网络的泛化能力,样本数据被随机划分为训练数据集、测试数据集和验证数据集,其中训练数据集占70%,验证和测试数据集各占15%。搜索空间中训练函数有12种,神经元数量从5到20不等,隐含层激励函数有4种,输出层激励函数统一选择线性激励函数,对共768个不同结构的前馈神经网络进行训练。考虑到数据驱动模型的泛化能力,最终优选训练集MSE较佳情况下,测试集MSE最佳的网络结构,搜索过程结果见表1至表4(只展示了部分结果)。

表1 压气机出口压力起动段误差数据神经网络架构搜索结果

表2 压气机出口压力负荷调整段误差数据神经网络架构搜索结果

表3 压气机出口温度起动段误差数据神经网络架构搜索结果

表4 压气机出口温度负荷调整段误差数据神经网络架构搜索结果
由表1和表2可知,就压气机出口压力而言,对于起动段误差数据集,优选的神经网络结构为: 16个隐含层神经元,隐含层激励函数为径向基函数(radbas),训练算法为LM算法;对于全速空载段和负荷调整段误差数据集,优选的神经网络结构为:20个隐含层神经元,隐含层激励函数为双曲正切sigmoid函数(tansig),训练算法为LM算法。由表3和表4同理可知压气机出口温度各段数据集对应的优选神经网络结构。最终得到的压气机出口压力三个运行状态下的解析模型如式(14)、式(15)和式(16)所示。
起动状态:
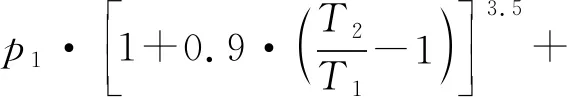
(14)
全速空载状态:
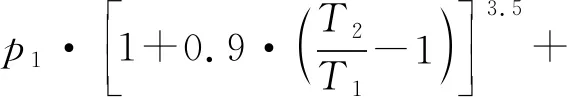
(15)
负荷调整状态:
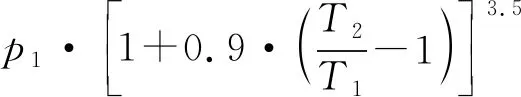
(16)
最终得到的压气机出口温度三个运行状态下的解析模型如式(17)、式(18)和式(19)所示。
起动状态:
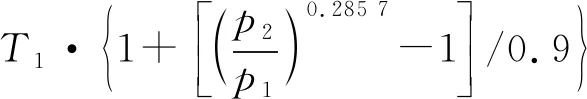
(17)
全速空载状态:
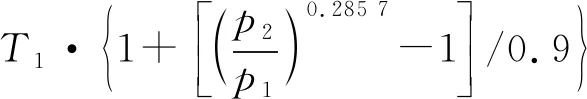
(18)
负荷调整状态:
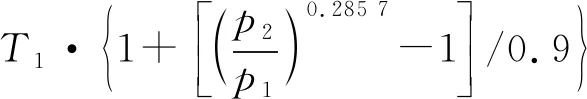
(19)
式中:权值矩阵W和偏置矩阵b的上标1、2、3分别表示起动状态、全速空载状态、负荷调整状态。
使用验证数据对未补偿的机理模型和最终的解析模型进行仿真,压气机出口压力仿真结果如图6所示,图7表示压气机出口压力机理模型在未补偿前以及补偿后(解析模型)的相对误差;压气机出口温度仿真结果如图8所示,图9表示压气机出口温度机理模型在未补偿前以及补偿后(解析模型)的相对误差。
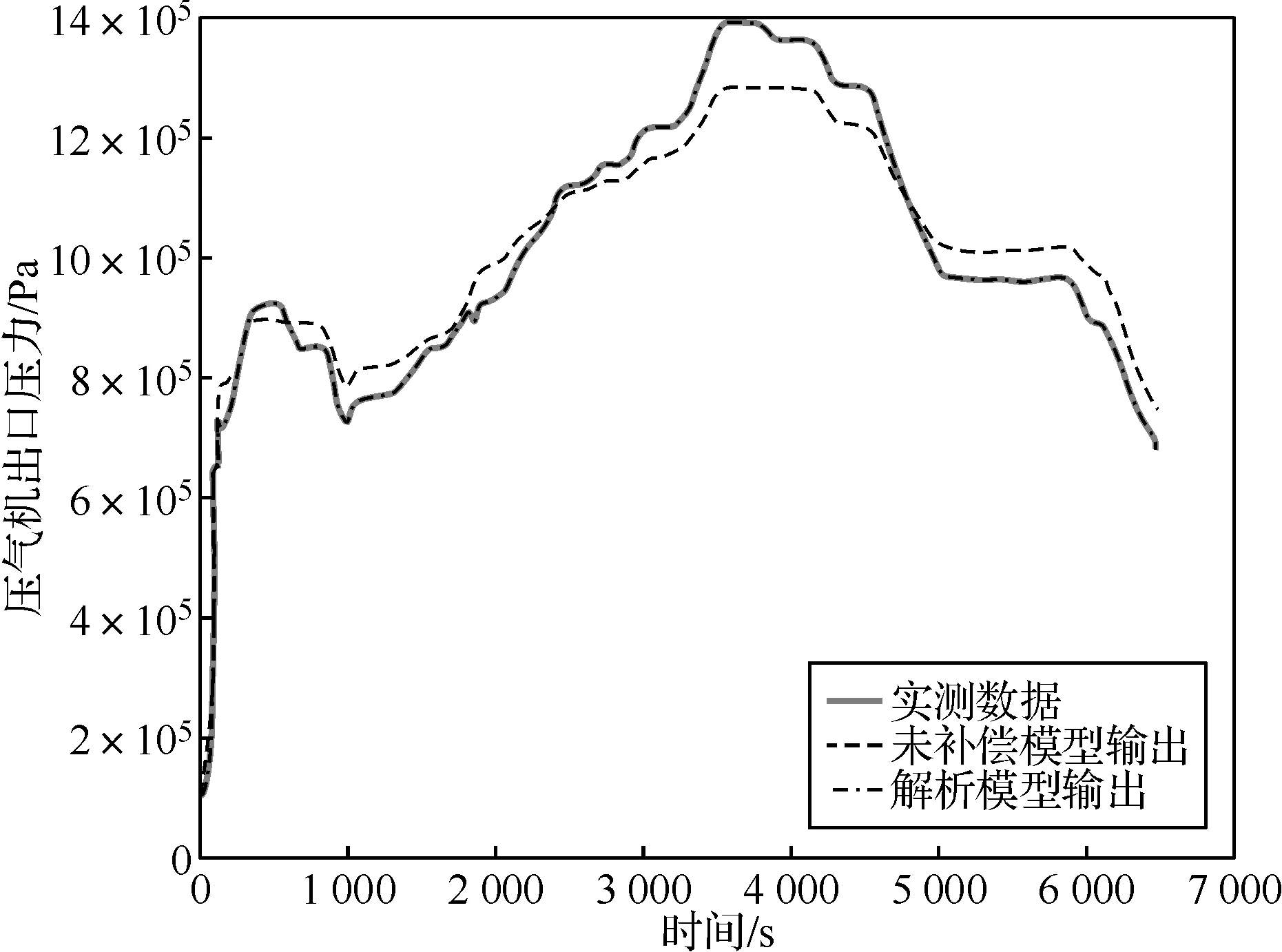
图6 压气机出口压力仿真结果

(a) 机理模型相对误差

图8 压气机出口温度仿真结果

(a) 机理模型相对误差
以上仿真结果表明,机理模型未进行误差补偿前,能够反映出参数在整个燃气轮机运行过程中的变化趋势,但精度低。通过数据驱动模型补偿后,误差明显下降,解析模型输出结果与实际测试结果几乎重合,相对误差都在2.5%以下,达到解析余度设计要求。且验证数据并未参与数据驱动模型的训练,因此仿真结果也反映了解析模型具有一定的泛化能力。再将本文的仿真验证精度与现役某重型燃气轮机的传感器模型精度作对比,对比结果见表5。经对比,发现基于本文提出的机理数据协同驱动方法建立的解析模型,精度提升都在80%以上,而且能适用于重型燃气轮机的主要运行状态。
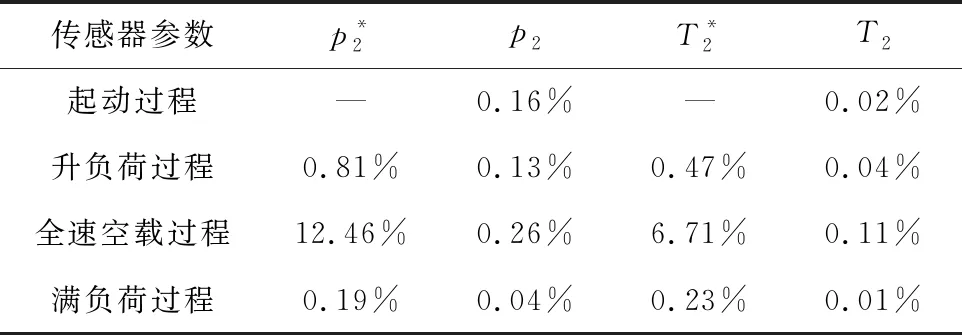
表5 机理-补偿参数解析方法与GE某重型燃气轮机传感器模型的精度对比
3 结论
本文提出一种机理数据协同驱动的控制系统传感器参数解析余度设计方法,从重型燃气轮机工作原理出发,分析工质的循环过程,建立典型工况下的传感器参数机理模型;根据重型燃气轮机工作过程将运行数据分为三段,对应燃气轮机工作的三个状态,引入网络架构搜索方法,采用前馈神经网络来训练机理模型与实测数据间的误差。由仿真结果可得出以下结论:
(1) 本文提出的参数解析余度设计方法适用于重型燃气轮机的主要工作状态,且精度高于现役重型燃气轮机传感器模型精度。
(2) 本文所提解析方法思路清晰,易于实现。机理模型的建立过程简单,且具有通用性,其结果能够反映重型燃气轮机运行过程中状态参量的变化趋势;前馈神经网络的拟合结果结构简单,易于编程实现,保证了解析精度。
(3) 本文建立的传感器参数解析余度模型,具有重要的实际工程应用意义,已应用到某重型燃气轮机容错控制系统研发项目中。

