辽宁省环境经济效率及其收敛性研究

吴 洋

（沈阳师范大学 国际商学院，辽宁 沈阳 110034）

0 引言

地方政府承担着经济建设的重任，同时，又是环境保护工作的主体，在促进经济健康发展的同时又要确保当地环境状况可控，对由于经济建设而带来的环境污染问题有着不可推卸的治理责任。辽宁省作为老工业基地，其面临的环境污染问题非常严峻。在既要保证经济发展速度，又要保证环境状况可控的前提下，辽宁省的经济与环境保护之间能否实现平衡发展值得研究。因此，从参考环境因素的角度出发，测算辽宁省的投入-产出经济效率，即环境经济效率，进而对效率值的变化趋势进行深入分析。

1 文献综述

目前，国内外学者从不同角度对环境经济效率进行了研究。IRAM 等[1]通过DEA 方法研究了2013-2017 年间主要OECD 国家的环境经济效率情况。SUZUKI 等[2]运用超效率的DEA 模型，采用能源消耗和人口数量作为投入，GDP 与二氧化碳排放量作为 产出测算2003-2012 年间欧盟、OPEC 组织和东盟国家的能源-环境-经济效率。SUBHASH等[3]运用DEA方法对2005年110个国家的环境数据进行了分析，以不同种燃料作为投入，将国内生产总值作为期望产出，将二氧化碳排放量作为非期望产出。林伯强等[4]运用非径向方向距离函数的超效率DEA 模型，研究中国地级以上城市的绿色 经济效率，通过工具变量法解决经济集聚与绿色经济效率之间的内生性，并研究了经济集聚对绿色经济效率存在先促进后抑制的现象背后的机制问题。林进忠等[5]运用DEA-SBM 模型测算中国省际的绿色经济效率，并从总体时序、空间特征、省际差异等方面进行剖析，分析了经济集聚对本地及邻近省份绿色经济效率的作用，并提出对策 建议。胡晓琳[6]则着重研究省际环境经济效率的测算及其收敛性和影响因素，选用与Malmquist 模型相结合的DEA-EBM 模型，测算了2002-2013年中国各省份的环境效率及环境全要素生产率，认为省级环境全要素生产率的差异会持续存在，并提出相应的建议。张静等[7]研究汉江生态经济带11 个城市在2003-2015 年间的城市效率，其中考虑了生 态环境成本问题。李宏伟等[8]运用多期DID模型，研究了2005-2018 年黄河流域各城市的绿色经济效率，认为区域一体化政策促进了黄河流域绿色经济效率的提升，但政策作用只集中于中游地区，对上下游的影响不显著。张硕等[9]将河北省的11 个城市作为研究对象，考察了2010-2018 年河北省绿色经济效率，认为经济发展水平高的地区存在环境成本高的情况，而河北省整体的绿色经济发展水平不高。

通过对已有文献研究发现，个别文献对投入和产出指标的选取随意性较大，难以真实反映实际环境经济现状，特别是对环境污染指标的选取，通常采用总量指标而不是与地域面积相比较的相对量指标，所以结果存在偏差。选择传统的CCR 和BCC 模型居多，这类径向模型并不完全符合对环境经济效率的测度，因为并非所有的投入及产出指标都需要等比例扩大或缩减，同时有些文献还存在对DEA 模型的运用不够准确等问题。此外，尚未对当前辽宁省的环境经济效率及其收敛性进行研究。因此，从新的视角进行指标选取，运用窗口DEA-Hybrid 模型及条件β收敛检验对辽宁省2011-2019年14个城市的环境经济效率及其收敛性进行实证分析。

2 研究设计

2.1 研究样本与数据选取

选取2011-2019年辽宁省14个城市作为研究对象，数据来源于《辽宁省统计年鉴》。由于2011 年国家统计局和环境保护部对部分污染指标的统计口径进行了调整，所以本研究选取的时间跨度为2011-2019 年。测算环境经济效率就是在融入了环境因素的基础上测算一个经济体的投入-产出效率，因此在投入和产出指标的选取中需要加入环境因素指标。在投入指标中，选择城镇就业人数（城镇非私营单位就业人数和个体从业人数的总和）作为劳动投入，选择大中型工业企业资产总计作为资本投入，选择财政性环保支出作为政府的环保投入。在产出指标中，由于人均GDP 不仅可以代表一个地区 经济发展的状况也可以反映人民的生活水平，因此选择人均GDP 作为期望产出指标，代表经济产出成果；选择工业二氧化硫排放强度和工业废水排放强度作为非期望产出指标，代表对空气和水体的污染情况。如前所述，为了客观、准确地反映污染状况，对两种污染指标都进行了地域面积的相对化处理，即除以各城市的行政区域面积，得到两种污染物的排放强度指标[10]，具体见表1。

表1 指标说明 Tab.1 indicator description

研究选取的投入和产出指标共6 个，选择的城市共14 个，与决策单元（DMU）数量应大于投入和产出指标总数的3 倍这个DEA 使用的一般原则相对照有一定差距[11]。正因为如此，Hybrid 模型结合窗口模型，在测算效率值时会人为增加DMU 数量，即在每一个窗口中增加DMU 数量，从而提高了 DMU 效率值测算的准确度，避免了测算结果中效率值为1 的DMU 过多的现象。

2.2 模型构建

传统的CCR 或BCC 模型，各项投入和产出的扩大和缩减是等比例的，所以这类模型也叫径向模型，其缺点是各种产出都是弱可处置的，不能单独对某一个指标进行调整。SBM 模型可以将某个非期望产出设置为强可处置，所以不必在减少非期望产出时以牺牲期望产出为代价，即可以单独对某一个指标进行调整。但在现实生产中，有些指标是需要等比例改进的，而有些则不需要，此时就需要一种可以同时处理两种情况的模型，这就是Hybrid 模型。Hybrid 模型可以将投入与产出指标分为径向类指标和非径向类指标，如果所有指标均为径向，则Hybrid模型等同于径向模型；如果所有指标均为非径向，则Hybrid 模型等同于SBM 模型。选取的投入指标中，劳动投入和资本投入一般是等比例的，而环保支出的投入却不是。在产出指标中，各种污染物排放一般是等比例的，而人均GDP 这一产出指标就没有必要 随其他污染指标等比例缩放。所以从选取指标的特质来看，Hybrid 模型比较适合，比单纯的径向模型或SBM 模型更有优势。

为了测算综合技术效率，将规模报酬情况假设为不变，Hybrid 模型规划式的一般形式为

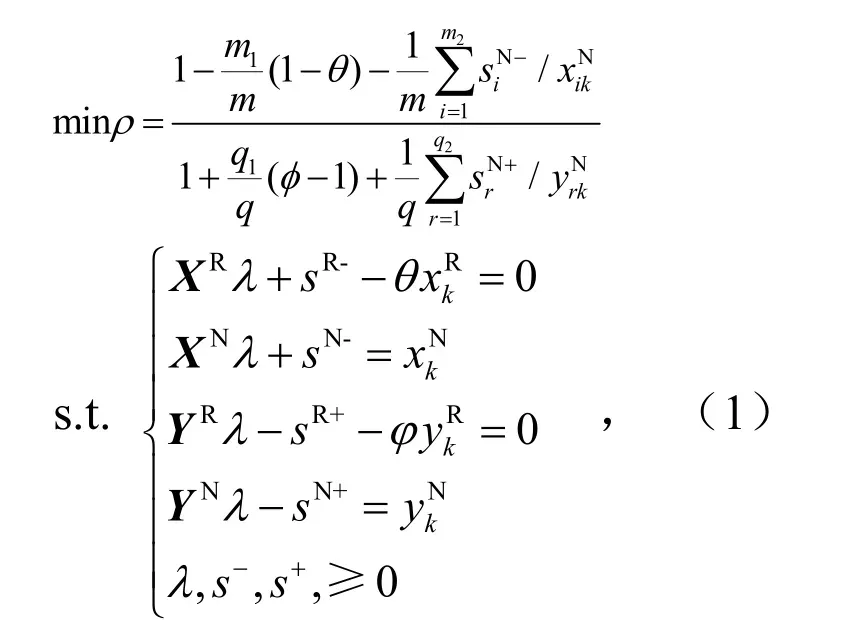
式中，si（i=1,2,…,m）为投入指标的松弛变量；sr(r=1,2,…,q)为产出指标的松弛变量；X为xi的矩阵；Y为yr的矩阵；R 为径向指标；N 为非径向指标；m为投入指标数量；m1为径向指标数量；m2为非径向指标数量；q为产出指标数量；q1为径向指标数量；q2为非径向指标数量；k为当前要测量的一个DMU 的标记[12]。

窗口模型严格来说是一种计算模式而非具体的模型，所以一般需结合其他具体模型来实现。窗口模型常运用于面板数据分析，设置连续3 至4 年宽度的窗口，将对应的面板数据放在一起作为参考集构建生产技术前沿面，测算决策单元DMU 的效率 值。然后将同一宽度的窗口按照时间顺序下移1 年，继续测算窗口中的DMU 效率值，以此类推，直至将窗口推行到最后1 年。最后，将同一个DMU 的多个效率值取几何平均值，即为该DMU 的效率值。此种方法的目的在于通过窗口增加DMU 的数量，使得测算的效率值更为精确，避免了因DMU 数量不足导致的效率值偏高的现象。

2.3 条件β收敛检验

条件β收敛检验是一种检验各经济体从长期角度看是否存在动态演化的趋势，各个经济体之间的经济差异是否随时间推移而缩小的一种检验方法。条件β收敛检验是相对于绝对β收敛检验而言的。绝对β收敛检验当中，各经济体趋于收敛的是同一个稳定状态，而条件β收敛检验中，各经济体趋向于各自的稳定状态，所以条件β收敛检验 中，假设不同经济体的基础条件和特征存在本质不同，承认发达经济体与欠发达经济体之间的差距始终存在[6]。因此，条件β收敛检验方法主要用于检验各经济体是否随时间推移而趋向各自的稳定状态。

3 环境经济效率值测算与结果分析

3.1 经济效率值测算

主要测算综合技术效率值，即假设各省 市的生产状态为规模报酬不变。考虑到需要保证就业和招商引资的政策条件，假设投入越小效率越高并不符合实际情况，而是要按照既定条件下产出越大效率越高的思路，所以窗口Hybrid 模型选择产出导向模型。关 于窗口模型的窗宽问题，一般的经验是选择窗宽为3 至4[13]，即一个窗口包括3 至4 年的面板数据，然后逐渐将固定的窗宽下移，进而可以将同一个DMU 测算出多个效率值。选用Hybrid 模型这种混合模型，需要 对各个指标的性质进行区分，由于劳动投入和资本投入存在一个最佳比例。因此，将投入指标中的城镇就业人数和大中型工业企业资产总计两项指标设置为径向指标，将财政性环保支出设为非径向指标。污染物是同时产生和排放的，因此将工业二氧化硫排放强度和工业废水排放强度两项指标设置为径向指标，将人均GDP 设置为非径向指标，Hybrid 模型才能更好地应用。在这些指标中，大中型工业企业资产总计、财政性环保支出、人均GDP，这3 个指标均通过GDP平减指数进行了平减处理，从而减少物价水平波动带来的影响。采用MaxDEA Ultra 8.19软件运行窗口Hybrid 模型对2011-2019 年辽宁省14 个城市的环境经济效率值进行测算。因篇幅所限仅列出沈阳、大连、鞍山3 个城市的环境经济效率值，具体见表2。

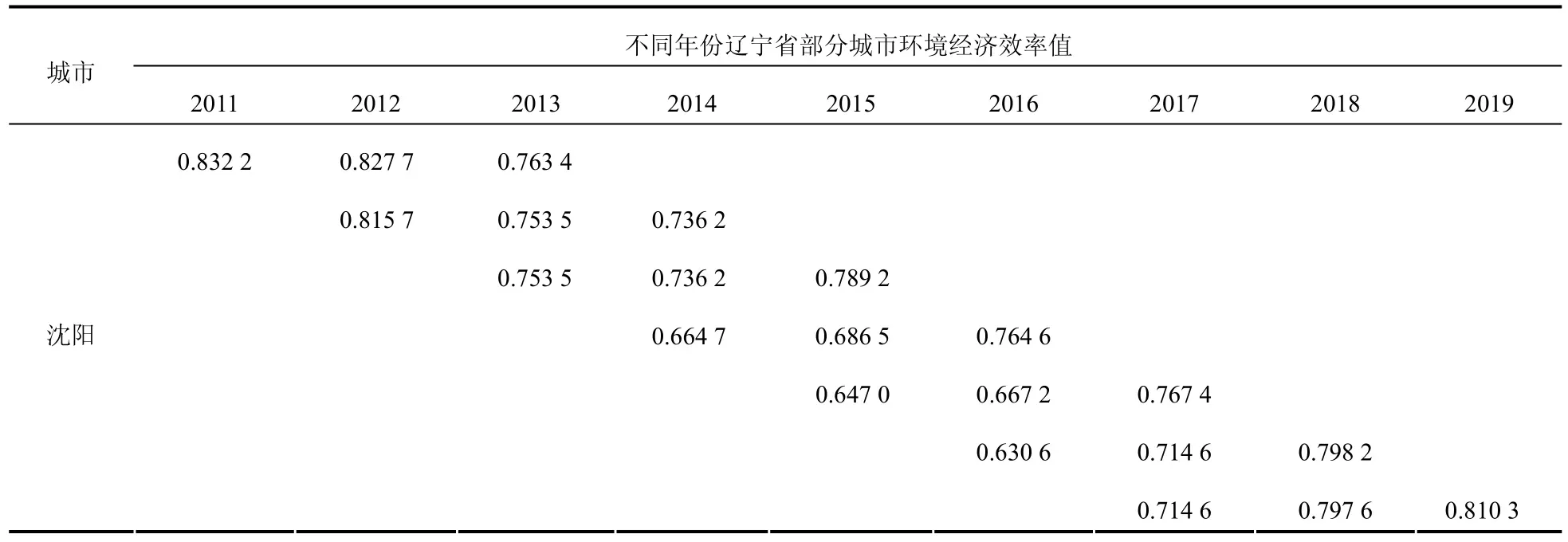
表2 2011-2019 年辽宁省部分城市环境经济效率值 Tab.2 environmental economic efficiency scores of some cities of Liaoning province during 2011-2019 by window Hybrid Model

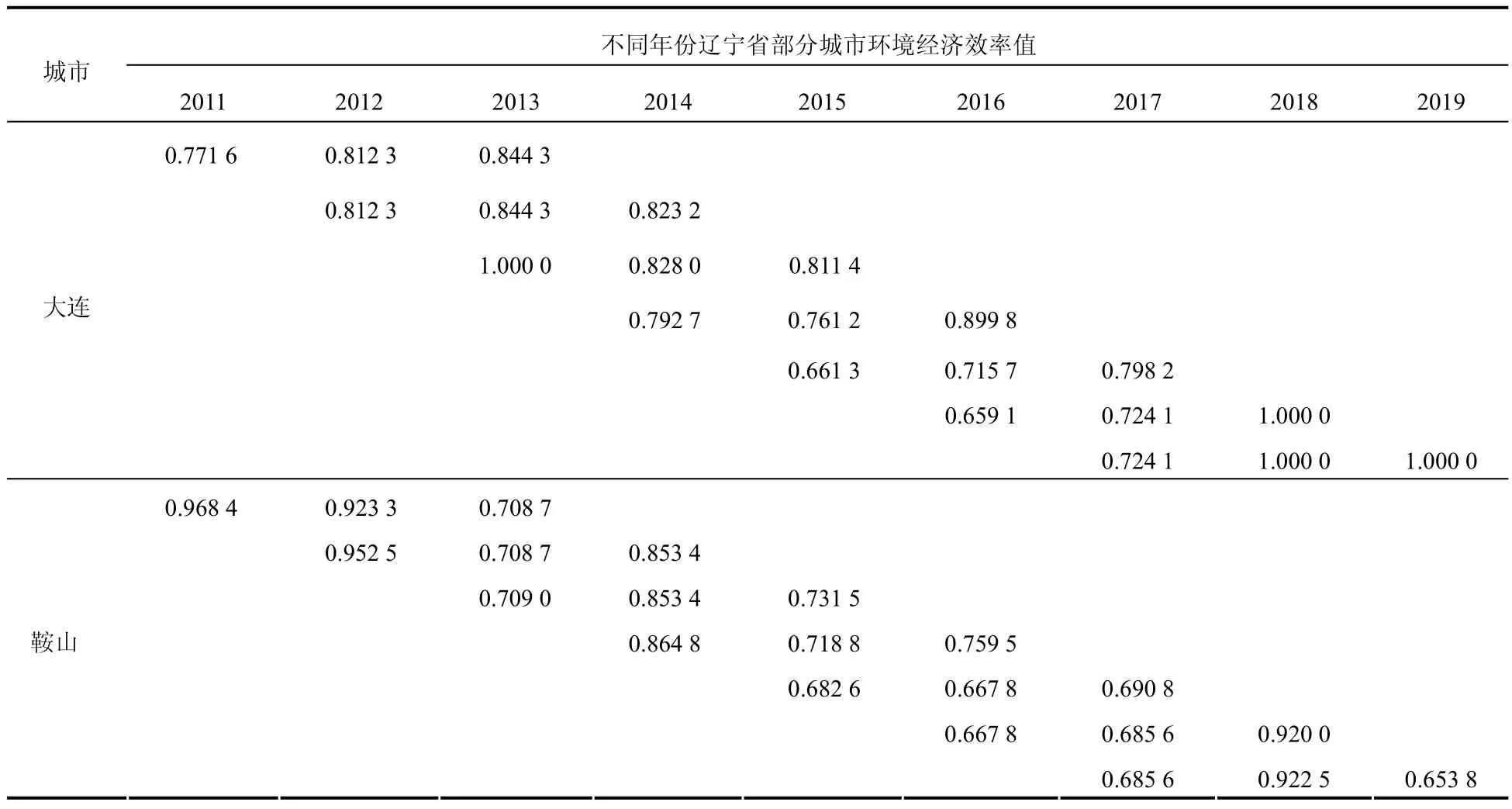
续表2

表2 是在窗宽为3 的条件下（如此共形成7个窗口）使用Hybrid模型测算出的结果。可以发现每一个DMU 除了2011 年、2019年之外，其他年份的效率值都不止一个。窗口模型的作用就是在DMU 数量不十分充足的情况下，通过设定窗口宽度，将多个横截面的DMU 放在同一个窗口下以增加DMU的数量，进而可以构建一个DMU 数量更多的生产技术前沿面，然后测算每个DMU 效率值。在窗口不断下移的过程中，每个 DMU 的效率值都会重新测算一次，从而使得效率值的测算结果更为精确。由于各个DMU 在部分年份中测算的效率值不止一个，为了达到有效分析数据的目的，可以将同一个年份同一个DMU 的不同效率值作几何平均处理，得到唯一的几何平均值，代表该DMU 在某年份中的实际效率值，这也是提高效率值准确性的一种方法[14]。将同一个DMU 多个效率值进行几何平均处理之后的辽宁省14个城市2011-2019年的环境经济效率值见表3。

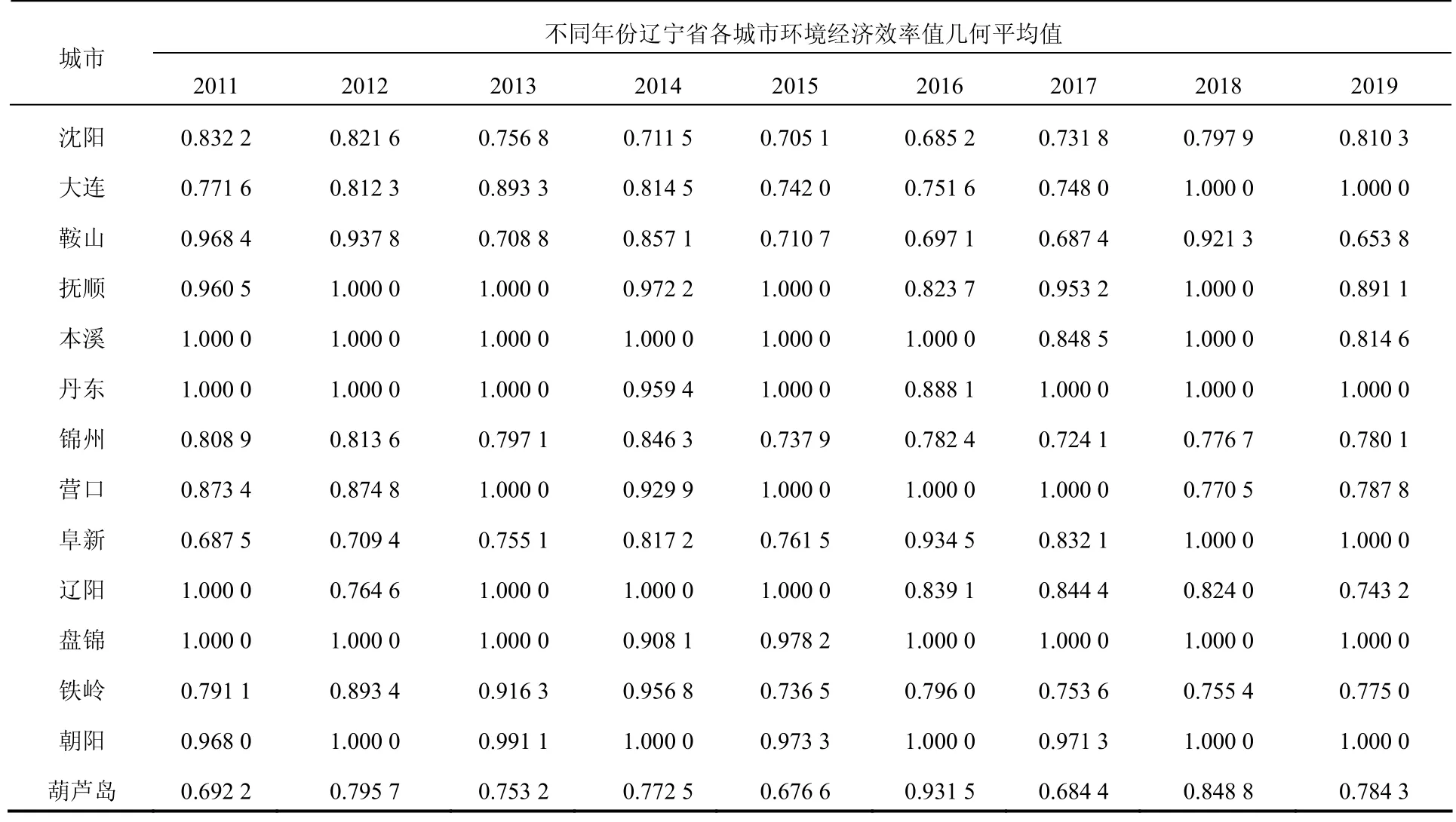
表3 2011-2019 年辽宁省各城市环境经济效率值几何平均值 Tab.3 geo-mean of environmental economic efficiency scores of all cities in Liaoning Province during 2011-2019

3.2 结果分析

通过对表3 中测算结果进行分析可以发现，首先，2011-2019 年辽宁省部分年份环境经济效率处于DEA 有效状态的城市有9个：大连（2 年）、抚顺（4 年）、本溪（7年）、丹东（7 年）、营口（4 年）、阜新（2年）、辽阳（4 年）、盘锦（7 年）、朝阳（5年），其余5 个城市在9 年中均未能处于DEA有效状态。这种差异主要源于各个城市人均GDP 以及环境污染物的排放强度。如果在 经济生产过程中，投入要素相对较少、人均GDP 相对较高、环境污染物排放强度相对 较低，则该城市的环境经济效率测算结果就会倾向于较高数值；反之，则会倾向于较低的数值。从这个角度看，环境经济效率值可以反映出各城市在经济发展与环境保护之间能否达到平衡，在经济发展的同时能否有效控制环境污染的情况。

其次，从2011-2019 年辽宁省各个城市的环境经济效率值变化来看，阜新的变化最大，从2011 年的0.687 5 上升至2018 年、2019 年的1，其环境经济效率值连续两年成为构成生产技术前沿面的效率值，变化十分显著。朝阳从2011 年的0.968 0 一路波动上升至2018 年和2019 年的1。大连从2011年的0.771 6 上升至2018 年和2019 年的1，上升的过程中波动幅度较大。盘锦的表现最为稳定，9 年间有7 年的环境经济效率值都处于生产技术前沿面上，在2014、2015 年中虽然效率值不是1，但也都在0.9 以上。相比之下，鞍山、营口、辽阳的环境经济效率值则呈现出波动下行的趋势。鞍山从2011年的0.968 4 下降到2019 年的0.653 8，营口从2011年的0.874 3下降到2019年的0.787 8，辽阳的环境经济效率值在2011-2015 年中有4年都达到了1，但从2016 年开始出现下滑，到2019 年跌至0.743 2。其他城市的环境经济效率值没有表现出明显的波动趋势。

经济发达与否、人口规模大小等导致的环境压力因素虽然能够对一个城市的环境经济效率值产生影响，但并非起决定作用。以沈阳和大连为例，大连在2011-2019 年，环境经济效率值明显波动上升，2018 年、2019 年都达到了1。而沈阳的环境经济效率值变化呈U 型，先由2011 年的0.832 2 下降至2016 年的0.685 2，又再升高至2019 年的0.810 3，但从未达到过1。这些都表明同为辽宁省经济发展速度较快、人口规模较大的城市，大连能够逐步达到经济发展与环境保护相平衡的状态，而沈阳则比较失衡。因此，环境经济效率值不仅受经济发展情况、人口规模的影响，还与各城市劳动和资本的投入比例、投入要素相互协调情况、生产技术与管理技术的高低、环保支出的使用过程、地方环保部门的环境治理手段与监察力度、各企业的配合情况等密切相关。数据包络分析模型的测算过程就是寻找能够最佳综合利用这些因素，进而使“投入-产出”过程的整体绩效最大化的那些DMU[15]。所以，环境经济效率值为1的城市就是全省14 个城市中经济发展与环境治理工作综合表现最好的城市，而那些环境经济效率值小于1 的城市就是综合表现尚有差距的城市。城市的环境经济效率值越低，其综合表现越差，说明其经济发展不充分，环境污染控制成效低。

3.3 收敛性分析

由于辽宁省的14 个城市存在经济发展基础与环境污染情况的既定差异，且这种差异在短期内将持续存在。因此，采用条件β收敛检验方法，将辽宁省 14 个城市2011-2019 年的环境经济效率值整合可得到一组面板数据，以此为依据进行分析。对于条件β收敛的检验方法，胡晓琳[6]根据先验理论，采用构建条件β收敛回归模型的方法进行检验。

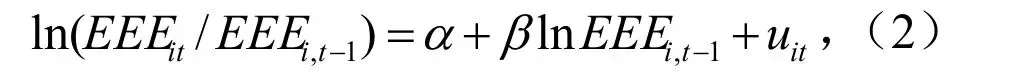
式中，EEEit为第i个城市第t期的环境经济效率值；EEEi,t-1为第i个城市第t-1 期的环境经济效率值；β为模型的回归系数；α为面板数据模型固定效应截距；uit为随机干扰项。

使用EViews10.0 软件对模型进行回归检验，基于样本面板数据的情况选择个体固定效应和时间固定效应，并选择交叉权重系数法（Cross-Section Weights）的面板校正标注误方法（Panel-Corrected Standard error），以便一定程度上解决复杂的面板误差问题，如同步相关、异方差、序列相关等。模型回归结果见表4。

表4 条件β收敛回归结果 Tab.4 results of conditional βconvergence regression

在回归结果中，β分别为-0.117 4、-0.834 6，均在1%的水平上显著。德宾-沃森统计值为2.142 6，模型拟合度为0.490 9、调整拟合度为0.372 1，表明回归结果良好。2011-2019 年辽宁省14 个城市的环境经济效率值存在条件β收敛现象，各城市的环境经济效率值呈向其自身稳定状态收敛的趋势，其环境经济效率值的变化路径逐渐趋于稳定。这种收敛趋势的收敛速度可以通过式（3）进行测算[6]。

式中，β为回归系数；T为基期和报告期的时间跨度；λ为收敛速度。

通过式（3）计算出λ的数值为0.224 9，表明辽宁省14 个城市的环境经济效率值以平均每年22.49%的速度向其各自的稳定状态收敛。

条件β收敛检验的结果表明，2011- 2019 年辽宁省14 个城市的环境经济效率值呈现向各自稳定状态收敛的趋势，表现良好的城市继续向着良好的稳定状态收敛，表现欠佳的城市也继续向着各自欠佳的稳态收敛，即无论该城市在处理经济发展与环境保护之间的关系方面表现得如何，都在趋于稳定。由此可以推断，如果2011-2019 年辽宁省14 个城市为保持经济发展与环境保护之间的平衡而采取的措施得当，则该城市的环境经济效率值就会慢慢向良好的方向收敛或一直处于良好状态；而如果措施欠佳，则其环境经济效率值就会向欠佳方向收敛或一直处于欠佳状态。因此，对于表现欠佳的城市，如果采用一贯的措施就会一直处于表现欠佳的状态。所以，需要打破固有惯性思维，进行政策调整。

4 结论

2011-2019 年辽宁省14 个城市在参考了环境因素条件下的环境经济效率值可以直接反映该城市在协调经济发展与环境保护之间的平衡能力。通过运用窗口Hybrid 模 型测算和条件β收敛方法检验发现，2011-2019 年辽宁省14 个城市很多都处于DEA 无效率状态且各城市环境经济效率值存在分化现象。从整体来看，环境经济效率值出现了下降，从经济发展和环境保护的综合表现上来看，各个城市都在向各自的稳定状态逐步收敛。所以，辽宁省的环境经济效率情况并不乐观，未能充分实现经济发展与环境保护的平衡。大部分城市经济发展不够充分，环境状况管控不佳。为此，辽宁省应积极制定应对策略，挖掘经济发展潜能，提高环境保护成效。