铝合金环槽铆钉连接节点弯矩-转角关系
冯若若,张铮,邵珂珂
(福建工程学院 土木工程学院,福建 福州 350118)
由于热输入影响,铝合金焊接热影响区内材料强度显著下降[1],故铝合金结构一般采用机械连接,主要包括高强螺栓连接与环槽铆钉连接。铝合金与钢材直接接触会发生电化学腐蚀从而降低节点的耐久性,不锈钢制成的环槽铆钉更适用于铝合金梁柱节点的连接。
目前,铝合金结构环槽铆钉连接节点的研究取得一定成果,多集中在板式节点上[2-4]。近年来国内学者针对铝合金框架环槽铆钉连接梁柱节点开展了相关试验研究。王中兴等[5-6]对T型件及铝合金框架环槽铆钉连接梁柱节点分别进行拉伸与单调加载试验,研究了T型件破坏模式和几何构造参数及不同材料对梁柱节点破坏模式和初始刚度的影响。邓华等[7]对工程常用铝合金板件环槽铆钉搭接连接试件进行静力试验,考察铆钉孔径、端距、边距等参数对承载力的影响。张天熊等[8]对国产新型高强度不锈钢环槽铆钉连接进行一系列试验研究,给出了环槽铆钉单钉预紧力设计值及铆接顺序原则。由于框架结构在进行半刚性连接节点设计时,需保证节点的构造与假定的弯矩-转角曲线相符[9],而现阶段对铝合金框架环槽铆钉连接节点弯矩-转角关系的研究还不充分。建立有限元模型对节点进行数值分析,在验证有限元模型准确性及有效性的基础上分析不同参数对节点力学性能的影响,基于三参数模型得出形状系数近似计算公式,为工程应用提供参考。
1 建立有限元模型
利用有限元软件ABAQUS建立铝合金框架环槽铆钉连接梁柱节点数值模型。梁、柱均采用6061-T6牌号铝合金。截面尺寸均为H280 mm×160 mm×8 mm×10 mm,长度1 500 mm。角型连接件和环槽铆钉为S304不锈钢材料。环槽铆钉整体构造复杂,故在有限元软件中选用简化模型[6]。节点构造和环槽铆钉简化模型见图1和图2。

图1 节点构造示意图(单位:mm) Fig.1 Schematic diagram of the joint’s construction

图2 环槽铆钉简化模型Fig.2 Simplified model of swag-locking pin
1.1 材料本构关系
铝合金材料的应力-应变关系采用Ramberg-Osgood模型来描述:
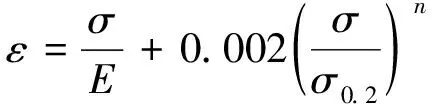
(1)
式中,n为应变硬化系数,一般根据Steinhardt的建议[10]取n=σ0.2/10;σ0.2为残余应变0.2% 时对应的应力,MPa;E为初始弹性模量,GPa。
对于不锈钢材料,Rasmussen进一步提出了基于公式(1)的修正模型[11]。
当σ≤σ0.2时
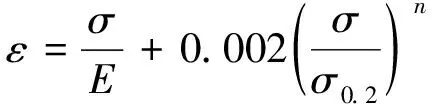
(2)
当σ>σ0.2时

(3)
其中,n=ln20/ln(σ0.2/σ0.01);E0.2为残余应变0.2% 时对应的弹性模量,E0.2=E/(1+0.002nE/σ0.2);m为应力大于σ0.2时的材料应变硬化系数,m=1+3.5σ0.2/σu;σu为极限应力,MPa;εu为极限应力对应的极限应变,εu=1-σ0.2/σu。
1.2 单元选取、网格划分与选定
有限元模型选用八节点六面体线性减缩积分单元(C3D8R),该实体单元求解比较精确,但存在沙漏问题,需要通过细化网格。为避免出现网格扭曲失效现象,在铆钉孔四周对部件进行切割处理。节点有限元模型网格如图3所示。

图3 节点有限元模型网格划分Fig.3 Joint’s finite element model meshing
1.3 相互作用及边界条件
节点中存在很多接触,包括铆钉上下表面与梁、柱翼缘、铆钉与铆钉孔、角型件与梁、铆钉与角型件接触等。节点接触类型为面-面接触,法向采用“硬接触”,切向采用库伦摩擦,摩擦系数设置为0.3[6]。施加预紧力时,可沿中部截面将铆钉分为两部分,在该切分面上施加铆钉预紧力,设定铆钉预紧力为18.85 kN[12]。
节点柱端设置为铰接,梁端截面约束耦合点的面外位移及转角,模拟试验中设置侧向支撑的情况。
1.4 模型验证
选取文献[5]中试验模型TSAC-S1进行建模分析。将有限元所得结果与试验的弯矩-转角曲线进行比较,如图4所示,极限承载力误差为3.3%。通过对比可知,有限元模型计算结果与试验吻合较好。

图4 弯矩-转角曲线对比Fig.4 Moment-rotation curve comparison
由于节点有限元计算所得弯矩-转角曲线无明显下降段,因此,顶底角型件受拉区的应力或柱翼缘核心区域应力接近或刚达到材料的极限强度时,以出现局部塑性屈服区域为判定准则[13],认为此时节点发生破坏。
2 有限元参数分析
对32个模型进行参数化分析,表1给出了部分有限元模型的尺寸,1为基准模型,其他都是在基准模型的基础上改变参数得到。以下仅给出改变柱翼缘厚度(CFT试件)、梁截面高度(BH试件)、连接件翼缘厚度(AFT试件)和铆钉端距(SD试件)等影响较大的参数的结果与讨论。
除表1给出的部分参数取值外,其余参数取值分别为角型件翼缘taf厚度取6~14 mm,梁截面高度hb取240~280 mm,角型件与柱翼缘连接的铆钉中心到梁翼缘的距离g取44~64 mm,铆钉直径d取10~14 mm,梁翼缘厚度tbf取6~12 mm,梁腹板厚度tbw取6~12 mm,角型件与梁翼缘连接处螺栓的中心距pt取25~35 mm,角型件与梁翼缘连接处螺栓端距pe取31~41 mm。

表1 节点参数分析截面尺寸
注:表中H为高度,B为梁、柱和角型件翼缘宽度,tw为腹板厚度,tf为翼缘厚度。
2.1 柱翼缘厚度
为研究柱翼缘厚度变化对节点连接性能的影响,设计了CFT系列试件,其中CFT10为基准试件。CFT系列试件的有限元计算结果见表2。
由表2可见,柱翼缘厚度变化对节点的承载力和刚度有明显影响。CFT8、CFT10与CFT6试件相比,初始刚度分别提高12.2% 、33.1%,极限承载力分别提高26.8% 、53.4%。随着柱翼缘厚度的增加,节点承载力变化很小,节点的初始刚度随厚度增大而增大。CFT14试件的极限承载力相对于CFT12试件仅提高0.9%。当柱翼缘厚度足够大时,角型连接件被拉弯,翼缘与腹板交接处先形成塑性铰,随后产生裂缝断裂。柱翼缘厚度较小时,发生撕裂破坏,破坏模式改变,成为影响节点连接性能的关键因素。
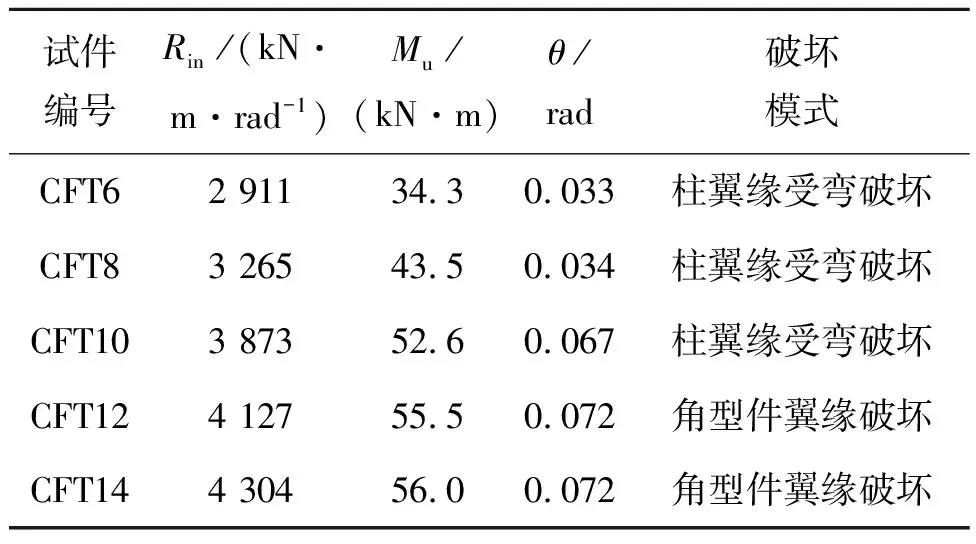
表2 CFT试件计算结果
注:表中Rin为节点的初始转动刚度,Mu为节点极限弯矩,θ为节点极限转角,下表同。
2.2 梁截面高度
为研究梁截面高度变化对节点连接性能的影响,设计了BH系列试件,计算结果见表3。
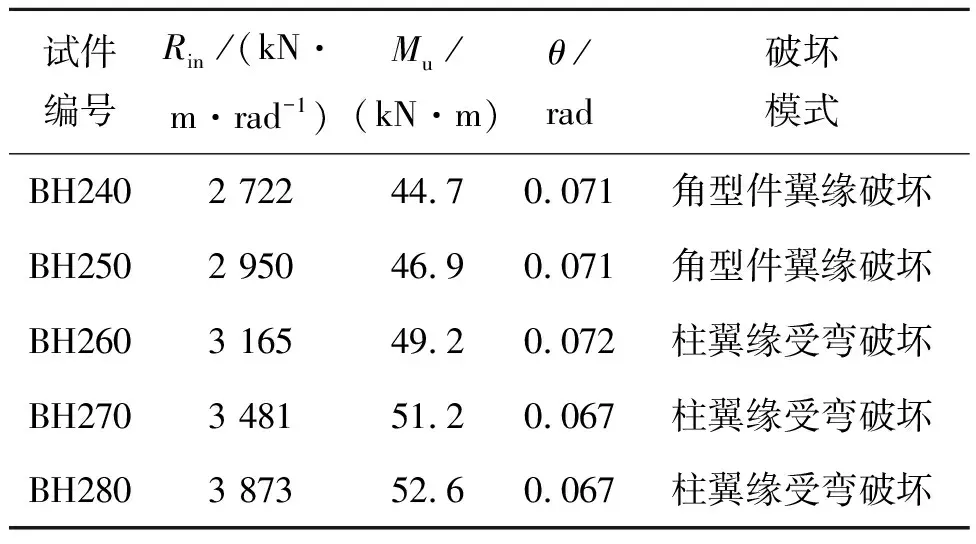
表3 BH试件计算结果
由表3可见,增加梁高对连接的初始刚度和极限承载力有一定影响。BH250、BH260与BH240试件相比,初始刚度分别提高了8.4%、16.3%,极限承载力分别提高4.9%、10.1%。BH270、BH280与BH260试件相比,初始刚度分别增加10.0%、22.4%,极限承载力分别增长4.1%、6.9%。梁截面高度增加时,其转动能力减小,承载力和初始刚度提高。
2.3 角型件翼缘厚度
为研究角型件翼缘厚度变化对节点连接性能的影响,设计了AFT系列试件,有限元计算结果见表4。
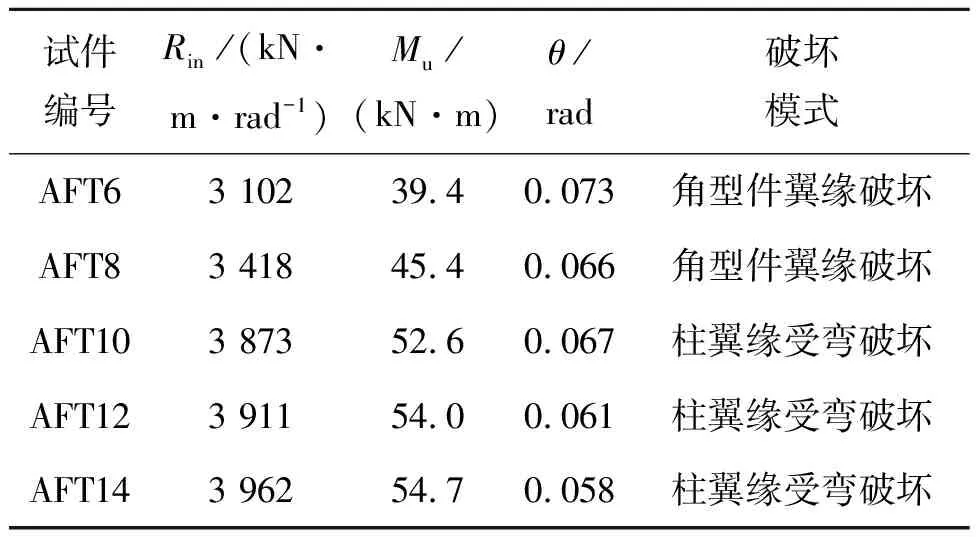
表4 AFT试件计算结果
由表4可见,角型件翼缘厚度变化对初始刚度和极限承载力有较大影响。AFT8 、AFT10与AFT6试件相比,初始刚度分别提高了10.2%、24.9%,极限承载力分别提高15.2%、33.5%。AFT12、 AFT14与AFT10试件相比,初始刚度分别增加了1.0%、2.3%,极限承载力分别增长了2.6%、3.8%,随着角型件翼缘厚度的增加,节点的初始刚度和极限承载力增长不明显。因此角型件翼缘应采取合适厚度,不宜过薄或过厚。
2.4 铆钉端距
为研究角型件与柱翼缘连接的铆钉中心到梁翼缘的距离变化对节点连接性能的影响,设计了SD系列试件,有限元计算结果见表5。
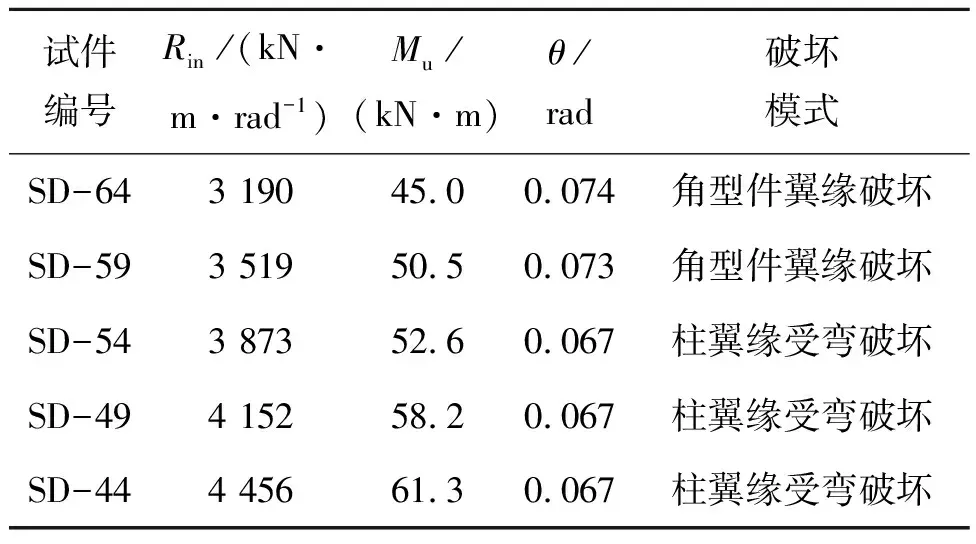
表5 SD试件计算结果
由表5可见,角型件与柱翼缘连接的螺栓中心到梁翼缘的距离越小,初始刚度和极限承载力越大。SD-59、SD-54与SD-64试件相比,初始刚度分别提高了6.2%、10.8%,极限承载力分别提高了12.2%、16.9%。SD-49、SD-44与SD-54试件相比,初始刚度分别增加4.2%、7.8%,极限承载力分别增长10.6%、16.5%。因此采用较小的端距有利于提高连接节点的初始刚度和承载能力。
3 三参数幂函数模型
用三参数模型模拟框架节点的弯矩-转角关系,能较好地模拟出M-θ的非线性特征,且表达形式简单。函数模型表达式为:

(4)
其中,Rki为连接的初始刚度,kN·m·rad-1;θ0为参考塑性转角,θ0=Mu/Rki;Mu为连接的极限弯矩,kN·m;n为形状系数。
三参数模型中Rki和Mu可通过数值分析求得,但形状系数n不具备具体的物理含义,可通过数值分析得到模型的弯矩-转角曲线,利用最小二乘法原理,拟合出形状系数n的值。表6给出32个环槽铆钉连接梁柱节点有限元模型的形状系数n的拟合值。
将表6中形状系数n的拟合值和所对应的参考塑性转角值θ0进行整理,如图5所示。利用最小二乘原理,拟合出一条直线来近似求解形状系数n的数值,该直线方程为:

表6 形状系数n的拟合值和近似值
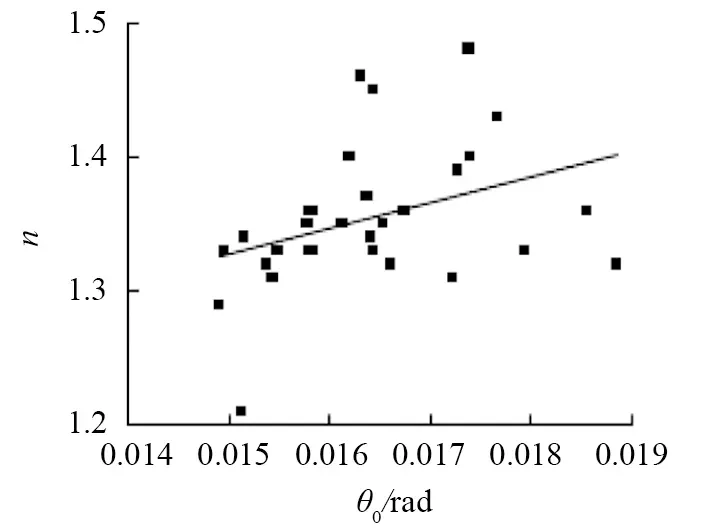
图5 形状系数n的散点分布及近似解Fig.5 Scatter distribution of shape coefficient nand its approximate solution
n=1.04+19θ0
(5)
选取试验数据[5]与拟合的弯矩-转角曲线进行比较分析,如图6和图7所示,得到的形状系数近似计算公式与试验结果吻合良好。

图6 试件TSAC-S2Fig.6 Test piece TSAC-S2
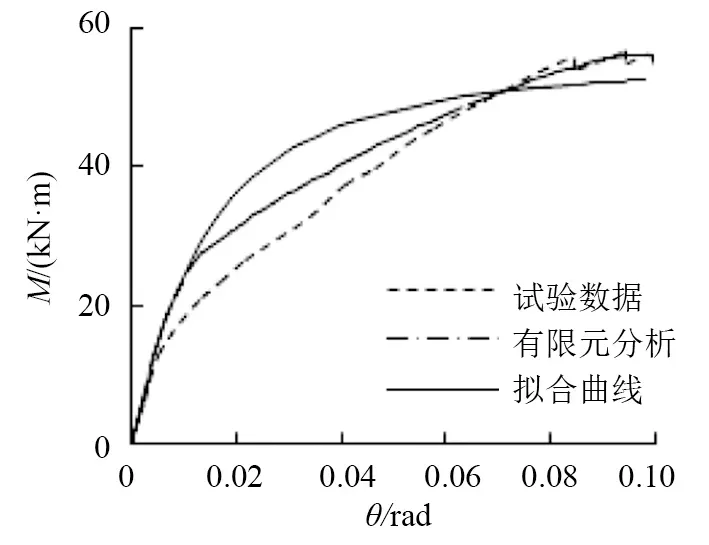
图7 试件TSAC-S3Fig.7 Test piece TSAC-S3
4 结论
1)采用的有限元方法在初始刚度、极限承载力和破坏模式等方面与试验结果吻合良好,可以较好地用于铝合金框架环槽铆钉连接梁柱节点的力学性能研究。
2)柱翼缘厚度和角型连接件翼缘厚度对节点初始刚度及承载能力影响显著。柱翼缘厚度较小时,其厚度每增加2 mm,节点的初始刚度提高10% 左右,极限承载力提高20 % 以上;厚度较大时,继续增加柱翼缘厚度对提高节点承载力的作用不明显。角型件翼缘厚度较小时,其厚度每增加2 mm,节点的初始刚度提高10% 左右,极限承载力提高15% 以上;厚度较大时,继续增加角型件厚度对提高节点初始刚度和承载力的作用均不明显。
3)梁截面高度变化和铆钉端距对节点的初始刚度及承载能力有较为显著的影响。梁截面高度每增加10 mm,初始刚度提高9% 左右,极限承载力提高5% 以上。角型件与柱翼缘连接的铆钉中心到梁翼缘的距离每减小5 mm,初始刚度提高8% 左右,极限承载力提高8% 以上。
4)针对铝合金框架环槽铆钉连接梁柱节点的弯矩-转角关系,基于有限元分析,得到三参数模型中形状系数n的近似计算公式,为工程设计提供参考。

