基于未确知测度理论公路隧道塌方风险评价
吴波,朱林萍,刘聪,李贻材,张耀
(1.东华理工大学 土木与建筑工程学院,江西 南昌 330013;2.中铁十一局集团第一工程有限公司,湖北 襄阳 441104)
隧道塌方是隧道施工中的常见事故,多造成严重的人员伤亡和财产损失[1],因此在隧道建设前实施科学有效的风险评价对于降低、预测和控制隧道塌方风险具有重要意义。2011年《公路桥梁和隧道工程施工安全风险评估指南(试行)》[2]出台,表明隧道风险评估的科学化与规范化越来越受到重视,同时也对风险评估方法科学性提出了更高的要求。
近些年,专家学者在隧道塌方风险方面做了大量的研究。戴世伟等[3]综合分析隧道塌方事故案例,采用N-K耦合模型对隧道塌方事故进行多因素耦合关联评估。关晓吉[4]通过可拓云模型理论对隧道塌方风险进行了评估。吕擎峰等[5]综合采用模糊层次分析法和后果当量法定量评估了隧道塌方风险可能性。陈舞等[6]将粗糙集理论和信息熵应用于山岭隧道塌方风险评价。王春河等[7]基于综合核对表法和专家调查法评价了隧道改扩建工程塌方风险。在评估隧道塌方风险和提供基本风险控制策略方面,Wu等[8]提出了一种综合采用贝叶斯网络、云模型、支持向量机的多源信息融合方法。王婧等[9]基于可变模糊集理论对铁路隧道塌方风险进行了评价。
评价指标权重确定是风险评价的基础工作,以上研究中采用的传统层次分析法等主观赋权法依赖专家经验,权重稳定性受到专家主观性和差异性影响。熵值法、粗糙集理论和云模型等客观赋权法虽受人为因素影响较小,但对客观数据依赖性强,存在部分客观数据难以获取的问题。运用组合赋权法可综合主客观权重两方面的信息,评价指标权重值确定更为合理。隧道塌方风险发生可能性难以建立精确数学模型予以量化,而未确知测度理论可作为一种量化方法处理此类不确定性问题。因此,本文提出一种基于博弈论法组合赋权和未确知测度理论的公路隧道塌方风险评价模型,并依托实际公路隧道工程验证该模型的适用性和可靠性。
1 公路隧道塌方风险辨识
公路隧道塌方风险因素众多,风险评价指标选取既要充分反映评价对象的重要风险因素,也要便于分析和计算。通过对当前研究成果[10-11]和公路隧道工程特点的综合分析,归纳出隧道塌方风险的主要影响因素包括围岩BQ值、断裂破碎带、偏压角度、地下水、年降雨量、隧道埋深、隧道跨度、施工方法、勘察设计等。将上述9个主要影响因素确定为二级指标,并进行归类得到三个准则层一级指标分别为工程地质、水文气象、勘察设计与施工。规范[2]给出的公路隧道塌方风险接受准则见表1,由此确定隧道塌方风险评价指标具体分级标准见表2。

表1 塌方风险接受准则
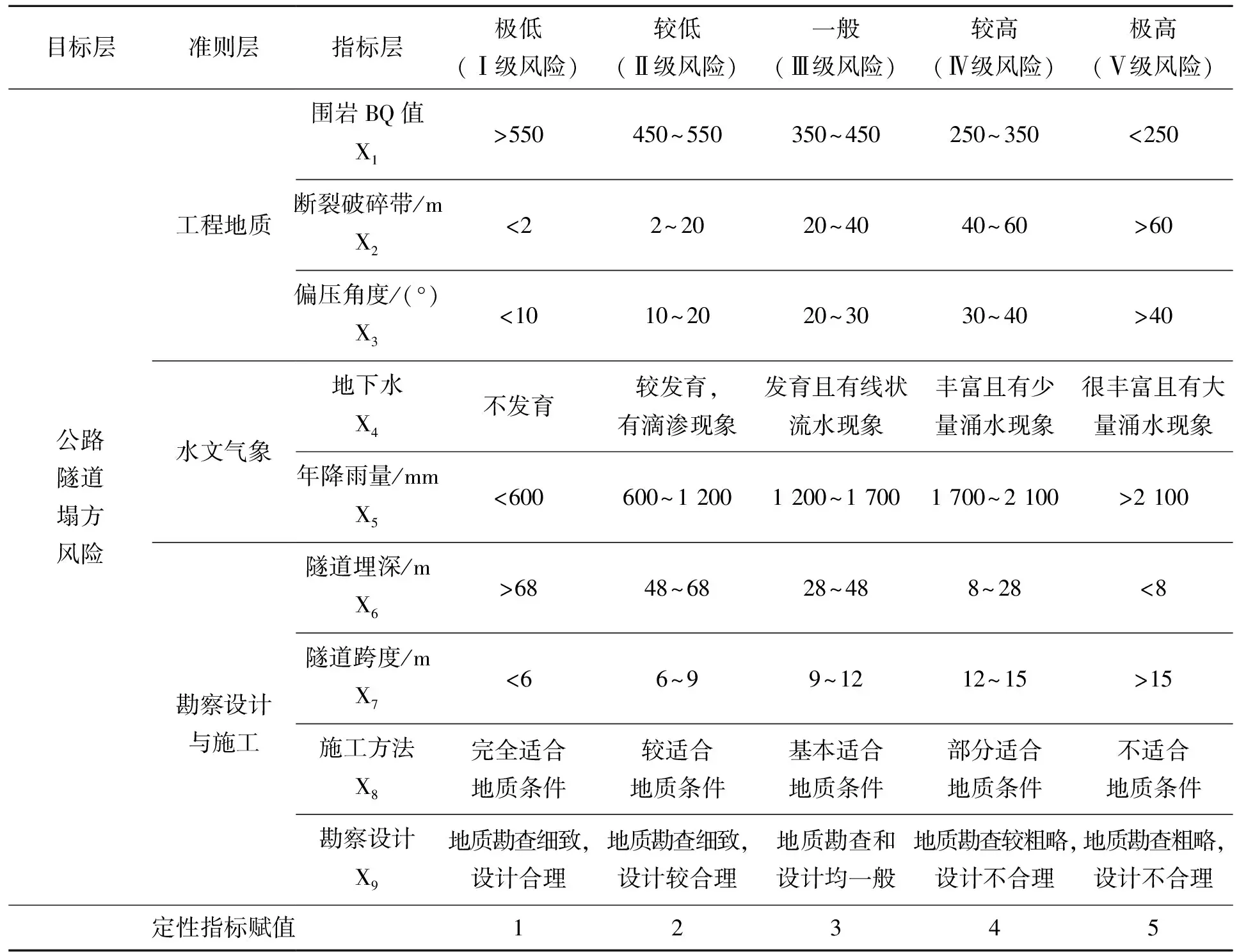
表2 公路隧道塌方风险评价指标与分级标准
表2中定量指标以数值范围形式描述所属风险等级,包括围岩BQ值、断裂破碎带、偏压角度、年降雨量、隧道埋深和隧道跨度6个定量指标。定性指标以定性描述的形式定义相应风险等级状态,并通过赋以分值实现量化,包括地下水、施工方法和勘察设计3个定性指标。
2 公路隧道塌方风险评价模型
2.1 未确知测度理论基本原理
设有n个被评价的公路隧道施工段,则待评价的公路隧道施工段空间向量可表示为R={r1,r2,…,rn}。各被评价隧道施工段ri(i=1,2,…,n)有m个评价指标空间,即X={x1,x2,…,xm},则可构成m维观测向量Ri={ri1,ri2,…,rim},其中rij表示公路隧道施工段ri的第j个评价指标观测值。将观测值rij划分为p个风险等级,则U={C1,C2,…,Cp}为rij的评价空间。若Ck>Ck+1或Ck+1>Ck,则称{C1,C2,…,Cp}为评价空间的一个有序分割类。
2.1.1 单指标测度评价向量
设μijk=μ(rij∈Ck)表示观测值rij属于第k个风险等级Ck的程度,若μ满足式(1),则称μ为未确知测度。
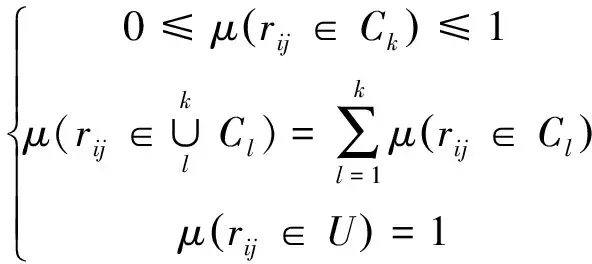
(1)
式中:i=1,2,…,n;j=1,2,…,k。
根据未确知测度定义,μ(rij∈Ck)为隧道塌方风险评价单指标测度函数,各评价指标测度值μijk构成的单指标测度评价矩阵可表示为
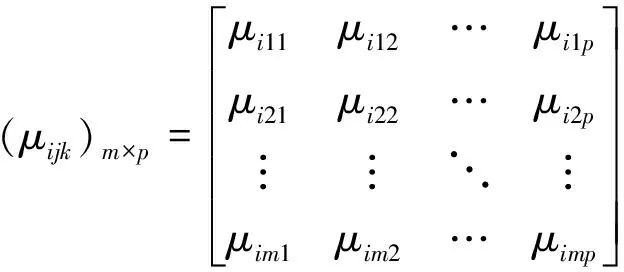
(2)
2.1.2 单指标测度函数
根据表2中评价指标取值范围以及单指标测度函数定义绘制单指标测度函数图,如图1、图2所示。
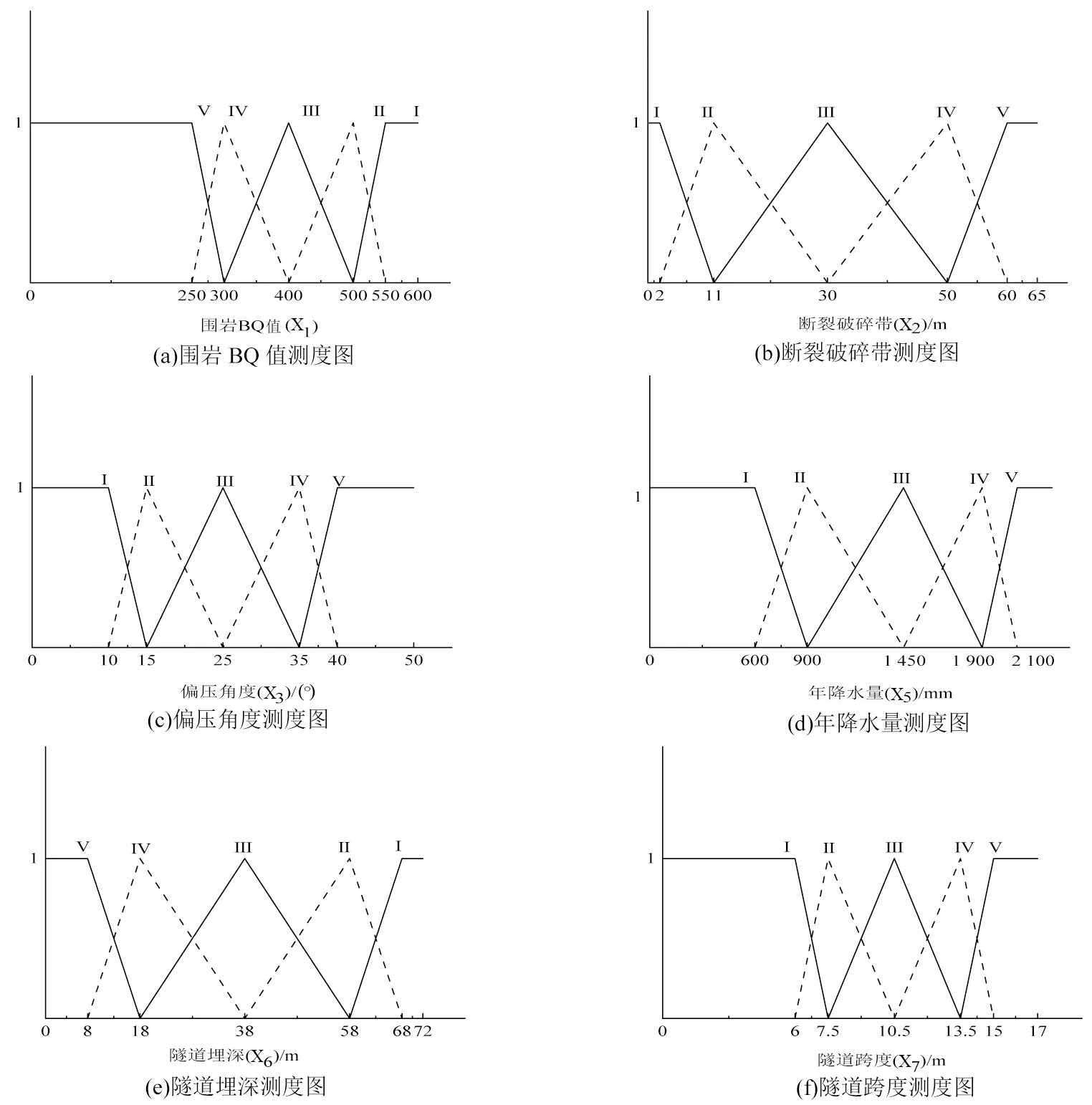
图1 定量指标单指标测度函数图Fig.1 Single indicator measurement function graph of quantitative indicators
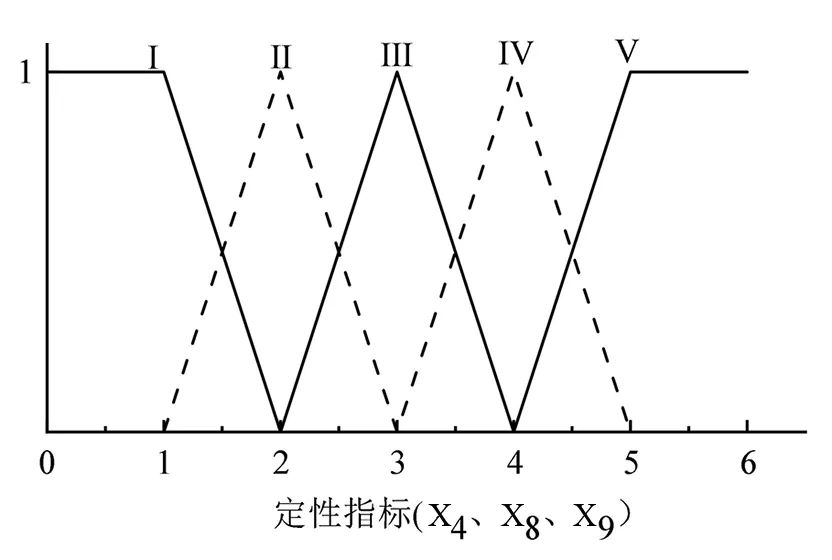
图2 定性指标单指标测度函数图Fig.2 Single indicator measurement function graph of qualitative indicators
2.2 博弈论法组合赋权
2.2.1 评价指标主观权重确定
层次分析法(AHP)由美国学者Saaty提出,是一种常用的主观权重计算方法。当涉及因素较多时,因素重要度排序过程复杂且计算量较大,判断矩阵需进行一致性检验。由于专家主观差异性,常难以满足一致性要求,为此相关学者提出了3标度层次分析法(improved analytic hierarchy process,IAHP)[12]。IAHP法可有效简化各因素重要度确定的复杂过程,其计算结果精度高、收敛快,不必进行一致性检验。
专家通过比较因素ai和aj的相对重要性程度来构建判断矩阵A=(aij)n×n,见表3。

表3 矩阵各元素取值规则(IAHP法)
对判断矩阵行求和从而得出重要性排序指数si,如公式(3)所示。通过公式(4)和(5)计算得到间接判断矩阵B=(bij)n×n。
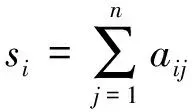
(3)
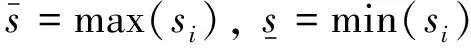
(4)
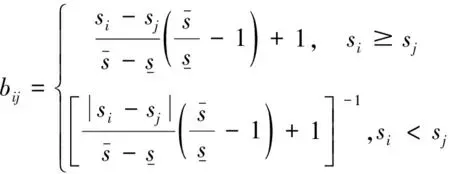
(5)
构造拟优一致矩阵B′=(b′ij)n×n,由公式(6)确定矩阵各元素。通过计算拟优一致矩阵B′的特征向量得出同一指标层各指标因素的权重值wi,计算方法见公式(7)。
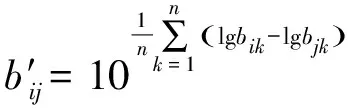
(6)
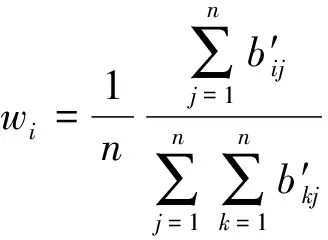
(7)
2.2.2 评价指标客观权重确定
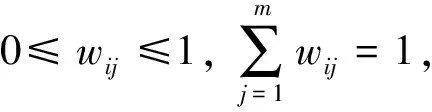
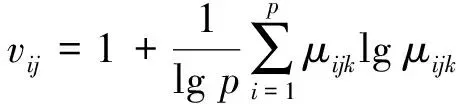
(8)
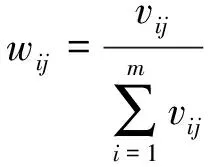
(9)
2.2.3 博弈论法确定评价指标组合权重
为同时考虑主客观权重影响,采用博弈论法计算评价指标组合权重。博弈论组合赋权旨在建立不同方法所确定权重间的线性优化组合[13],并取得优化权重与不同权重计算方法所得权重之间的平衡。
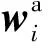
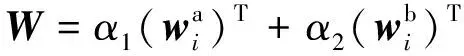
(10)
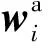
q=(1,2)
(11)
式(11)的最优化一阶导数条件如下:
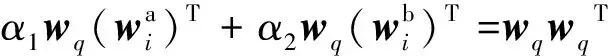
(12)
计算得到α1和α2的值后进行归一化处理,如式(13)所示
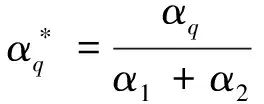
(13)
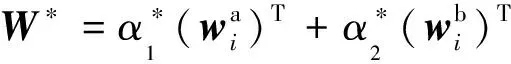
(14)
2.3 多指标综合测度及风险等级确定
根据评价指标组合权重值求出隧道施工段ri的多指标综合测度:

(15)
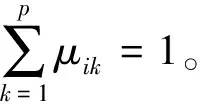
显然μik满足公式(1),那么可称μik为测度。ri的多指标综合测度评价向量为{μi1,μi2,…,μip},依据置信度识别准则确定隧道施工段塌方风险等级,其计算过程如下:设λ为置信度(λ≥0.5),若C1 (16) 此时可知待评价的公路隧道ri属于第k0个评价类Ck0。 福建莆炎高速公路鱼塘溪隧道为双线分离式小净距隧道,位于丘陵区,山坡基岩出露较差,地表为第四系坡残积土层覆盖。隧道右线最大埋深107 m,主要位于Ⅳ、Ⅴ级围岩中。隧道洞口段存在大偏压地段,围岩由坡残积层与强风化层构成;隧道出口段围岩主要由砂质黏性土和全、强风化层构成。洞身岩体软硬相间,完整性较差;部分施工区段存在花岗岩侵入,节理、裂隙较发育。工程所处区域主要地下水类型为基岩裂隙水和第四系孔隙水,以基岩裂隙水为主。区域气候特征表现为雨水较多,且雨季暴雨集中。 3.2.1 鱼塘溪隧道塌方风险评价指标 根据前文的分析,选取6个定量指标和3个定性指标,即围岩BQ值(X1)、断裂破碎带(X2)、偏压角度(X3)、地下水(X4)、年降雨量(X5)、隧道埋深(X6)、隧道跨度(X7)、施工方法(X8)、勘察设计(X9)。本文确定4个典型施工区段作为风险评价对象。表4中T1为隧道洞口段样本,T2为隧道进口段样本、T3为隧道洞身段样本、T4为隧道出口段样本。综合鱼塘溪隧道设计资料和现场调查结果,得到各隧道施工区段相应评价指标的调查数据如表4所示。 表4 鱼塘溪隧道评价指标调查数据 对选取的典型评价指标说明如下,围岩BQ值(X1)越高,代表围岩越稳定。断裂破碎带(X2)反映岩体完整性,岩体结构完整则地质风险较小。偏压角度(X3)越大,隧道开挖后产生的围岩应力重分布越不利。地下水(X4)和年降雨量(X5)综合反映水害对隧道塌方风险的影响,地下水发育和雨水较多会显著增加隧道塌方发生可能性。隧道埋深(X6)越浅,则发生塌方风险可能性越高。隧道跨度(X7)反映隧道断面大小,隧道开挖断面越大则塌方风险越高。 3.2.2 博弈论法计算评价指标组合权重向量 采用博弈论法将3标度层次分析法计算所得主观权重与熵值法计算所得客观权重进行耦合,以样本T1为例,计算过程如下: (1)根据单指标测度函数的定义以及表4中鱼塘溪隧道各评价指标的取值,结合前文所述计算方法求出隧道施工段单指标测度值μijk,把求出的单指标测度值进行整理,进而得到样本T1单指标测度评价矩阵如下: (17) (4)博弈论法计算样本T1相应评价指标组合权重向量:根据公式(10)~(15)将IAHP法和熵值法的计算结果耦合得出样本T1评价指标组合权重向量:W*={0.112 9, 0.130 7, 0.094 5, 0.126 1, 0.168 7, 0.121 3, 0.117 1, 0.071 6, 0.057 1}。 3.2.3 隧道塌方风险多指标综合测度评价向量 将计算得到的塌方风险评价指标组合权重向量与评价矩阵进行矩阵运算,得到多指标综合测度评价向量: {0, 0.300 7, 0.193 0, 0.334 8, 0.171 5},取置信度λ=0.5,依据式(16)得:k0=0.828 5>0.5,由此判定该隧道洞口段T1塌方风险等级为Ⅳ级,属于较高风险。采用相同方法计算得到其他样本的多指标综合测度评价向量并确定隧道塌方风险等级,如表5所示。 表5 鱼塘溪隧道塌方风险等级 (1)由表5可知隧道洞口段样本T1塌方风险等级为Ⅳ级,属于较高风险。隧道洞口段围岩稳定性较差,存在大偏压地质,埋深较浅且地下水丰富。同时,通过现场调查发现洞口段开挖后未成形的边坡也容易因为雨水的冲刷发生滑塌事故。 (2)样本T2和T3的隧道塌方风险等级为Ⅲ级,属于一般风险。调查资料显示隧道进口段围岩等级为Ⅳ级,属于小偏压地段,埋深相较洞口段更深,且受地下水影响较小;隧道洞身段围岩为Ⅲ级,属于无偏压地段,埋深最深,且地下水不丰富。 (3)现场评估结果将样本T4塌方风险可能性确定为较高,主要是考虑到隧道出口段为Ⅴ级围岩,虽属于无偏压地段且受地下水影响较小,但出口段埋深较浅,难以形成拱效应而易产生塌方事故。通过对比样本T4评估结果与现场评估结果可知,本文方法中未能考虑实际施工中隧道深埋段向浅埋段转换的动态施工过程,这是样本T4评估结果与现场评估结果产生差异性的主要原因。 (4)鱼塘溪隧道4个典型施工区段风险评估结果表明隧道洞口段塌方风险最高,为避免隧道洞口段塌方事故发生,在洞口段施工前必须先施作完成洞顶截水沟,增设临时排水设施,防止施工场地积水,并配备抽水泵。在隧道开挖过程中要随时掌握天气情况,提前进行施工防排水,避免雨水对未成形的边坡造成冲刷,从而引起滑塌。遇到极端降雨天气,应停止边坡开挖,人员机械撤离至安全区域,并对坡面喷射混凝土及时封闭。在汛期时要安排专人巡查,做好雨中、雨后检查,确认洞顶及边坡有无危险情况,发现后及时处理加固,同时加强洞顶、边仰坡的沉降监测频率,随时掌握沉降信息。 1)根据国内外大量隧道塌方案例统计资料、相关文献及规范,并结合公路隧道工程特点选取围岩BQ值、断裂破碎带、偏压角度、地下水、年降雨量、隧道埋深、隧道跨度、施工方法、勘察设计作为公路隧道塌方风险评价指标,避免评价指标单一的不足,一定程度上提高了评价结果的客观性和准确性,在公路隧道风险评估中具有较强适用性。 2)评价模型中将风险指标因素划分为5个等级,多数指标因素通过可测量的数据进行风险等级划分,避免指标因素因为模糊描述带来判断偏差。采用博弈论法组合赋权确定各评价指标的综合权重,能够综合反映主客观权重信息的影响,并基于组合赋权与未确知测度理论的风险评价模型对鱼塘溪隧道塌方风险进行评估,将评估结果与现场评估结果进行比较,验证了该模型应用于隧道塌方风险评价的可靠性。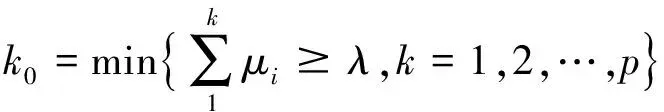
3 工程实例分析
3.1 工程概况
3.2 公路隧道塌方风险评价模型应用


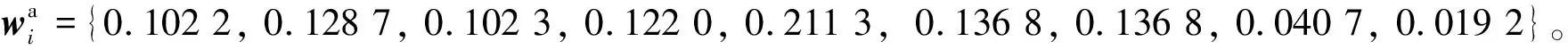
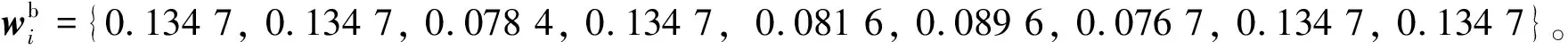

3.4 结果分析
4 结论

