地面瞬变电磁勘探中源外地形的影响

饶丽婷，武 欣，党 博，党瑞荣，李 勇

(1. 西安石油大学 电子工程学院,陕西 西安 710065; 2. 中国科学院地质与地球物理研究所中国科学院矿产资源研究重点实验室，北京 100029; 3. 北京中科地垣科技有限公司，北京 100190)

0 引 言

瞬变电磁法是近年来地球物理领域发展较快的一种重要方法，具有探测深度大、灵敏度高、方便快捷、成本低的特点，广泛应用于金属矿、石油、天然气、煤炭、地热、地下水等探测中。邱志忠等研究表明，地形是影响电磁场分布的主要因素之一。中国山地、高原、丘陵众多，这些起伏地形的国土面积约占总国土面积的2/3，复杂地形为中国矿产资源的发现和勘查造成了极大困难。目前，地面瞬变电磁勘探数据的处理与解释通常基于平坦地形；在复杂地形区域实施勘探工作时，若直接基于平坦地形进行数据处理与解释，容易将地形影响错误地解释为地下异常体，并掩盖地下真实目标体的响应，造成数据解释的较大误差。近年来，随着国内地形地质条件良好的矿产资源已逐步勘探完毕，为了进一步加大矿产资源的勘查力度，前人逐渐开展了考虑地形条件的电磁勘探法相关研究。2012年邱卫忠通过测道图判断不同尺寸回线源的地形影响特征，并针对不同情况给出了简单的地形校正方法；殷长春等分别在2015～2017年先后开展了起伏地形上航空电磁法的数值模拟研究，并探讨了山谷、山脊等简单地形条件对航空电磁场的影响规律；2016年薛国强等通过对地形影响基本规律、经典比值校正原理的分析，提出了一种高效且实用的地形影响校正算法；2019年曹凤凤基于有限元法计算了起伏地形条件下地空瞬变电磁响应，分析了地空瞬变电磁系统中地形效应在斜坡、山谷、山脊等典型地形条件下的影响特征；2021年齐彦福等通过结合非结构时间域有限元法和L-BFGS反演算法，成功实现了考虑关断时间的地面瞬变电磁三维带地形反演；2021年霍军鹏研究了倾斜地形对地面回线源的影响，提出倾斜地形校正方法，并将其成功应用于存在地形影响的陕北侏罗系煤田采空区探测工程中。

发射源下方存在地形起伏的情况，发射源、地形等多种变化参数的影响相互耦合，难以分离各种影响因素的作用，数据解释也异常困难。为了避免地形造成复杂影响，实际勘探中铺设发射源和接收点会尽量避开起伏地形，此时不需要考虑发射源形变，只需要考虑源外地形的影响。目前，对地形影响的分析大多从测道曲线图或者视电阻率断面图进行定性判断，较少从整个观测时间段内量化评估地形影响的程度。为了量化评估地形影响的程度，需要借助三维数值模拟方法分别获得带地形、不带地形的瞬变电磁响应。带地形的瞬变电磁响应可以利用各种数值方法进行模拟，如积分方程(IE)法、有限差分法、有限元(FE)法、有限体积法等。其中，有限元法凭借对复杂地电模型适用性强、形成的总体系数矩阵稀疏且对称、易于并行等优点，已成为解决电磁法三维正演问题应用最广泛的方法。本文在不考虑发射源形变基础上，基于有限元法计算了带地形的地面瞬变电磁响应。首先，以均匀半空间模型解析解和前人块状高导异常体模型的数值结果为标准，验证了瞬变电磁法三维正演建模与仿真的正确性；然后，在矩形回线源外构造了山脊地形、山谷地形，以均匀半空间的下阶跃响应为参考，将地形与发射源的距离、大地电导率、异常体电导率作为变化参数，给出了整个观测时间段内在不同接收点处地形造成的相对误差分布，分析并总结了源外地形对电磁响应的影响规律。

1 瞬变电磁三维正演方法

本文将利用COMSOL AC/DC模块的磁场接口进行瞬变电磁三维正演。COMSOL Multiphy-sics是一款以有限元法为基础，求解偏微分方程(单场)或偏微分方程组(多场)来实现真实物理现象的仿真软件，广泛应用在声学、化学反应、电磁学、流体动力学、热传导、微波工程、光学等诸多领域。其中，COMSOL AC/DC模块可以对电场、磁场和电磁场在稳态、瞬态、频域下的应用进行建模与仿真。该模块的基础理论是麦克斯韦方程组和边界条件，通过矢量有限元法求解给定几何模型的介质内电磁场分布。

为了简化麦克斯韦方程组的求解过程，COMSOL AC/DC模块引入了标量位函数和矢量位函数替代电场()和磁场()。其表达式为

(1)

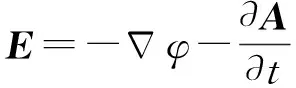
(2)

式中：为矢量磁位；为标量电位函数；为时间。

在准静态(不考虑位移电流)条件下，有限元法的时间域控制方程组为

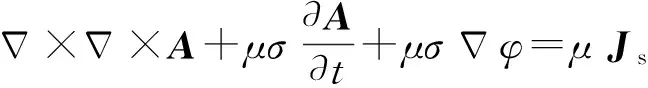
(3)

(4)

式中：为外加场源电流密度；为地电模型电导率；为磁导率，通常取真空中磁导率。

令Γ为计算区域外边界，为外边界单位法向量，采用自然Dirichlet边界条件，即

(×)=0

(5)

=0

(6)

根据矢量有限元法，利用弱公式化，对计算区域内模型的控制方程进行离散化，形成相应的数值模型方程组，然后通过迭代法或直接法求解各个网格单元处矢量磁位的近似解。具体离散过程可参考文献[22]。瞬变电磁法属于时间域电磁法，本文直接在时间域获得电磁场响应数值解，在COMSOL AC/DC模块的磁场接口下选择瞬态研究，时间步进方法选择后向差分公式。

电磁勘探法的频率一般较低，需要足够大的计算区域才能避免较为严重的截断效应，从而获得较为精确的数值解。为了兼顾精度和效率，在计算区域外围可以引入无限元域。无限元表示沿特定坐标轴拉伸的区域，其作用是近似形成无限大的域，有效避免截断效应。在每个坐标方向上，无限元域内实际建模坐标被归一化为0～1的无量纲坐标()；拉伸尺度可以定义为的函数(())，通过拉伸尺度函数得到经过延伸的坐标，可以认为是在给定方向上的新位置；在每个方向上分别拉伸，最终形成总拉伸区域。拉伸尺度函数表达式为

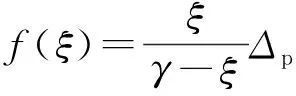
(7)

式中：为整个计算区域的对角线长度；为大于1的无量纲数字，由(+)/计算，其中为预设无限元域的拉伸厚度，应设置为远大于，以获得较大的拉伸值，一般可设置为1 000。

由式(7)可知，拉伸尺度函数具有非线性特征，靠近内边界的无限元域单元拉伸尺度较小，靠近外边界的无限元域单元拉伸尺度较大。

2 三维正演验证

本节将验证在COMSOL AC/DC模块的磁场接口下进行瞬变电磁三维正演的正确性。瞬变电磁法属于时间域电磁法，其观测时间范围广、电磁响应数值量级跨度大，对建模的细节参数(计算区域尺度、网格剖分、时间步长设置)非常敏感，不合理的建模参数会导致较大的误差。为了保证带地形的瞬变电磁响应计算以及后续分析的有效性，需要通过解析解以及前人已有数值解来验证瞬变电磁三维正演的正确性，从而获得合理的建模参数。本文的计算环境为Win10系统下的COMSOL Multiphysics 5.3版本，硬件为Intel(R) Core(TM) i7-8550U处理器、8G内存的个人笔记本电脑。

首先，基于均匀半空间模型进行验证。将地电模型设置为0.01 S·m的均匀半空间模型，矩形发射回线尺度为100 m×100 m，电流为1 A，接收点位于回线中心，这种情况下可以采用等面积的圆形回线中心点的解析解来检验其数值精度。均匀半空间三维正演建模如图1(a)所示。计算区域为半径5 km的圆球，球体被分成两个半球，其中一个半球作为大地区域，另一个作为空气区域。矩形回线源布设在大地半球与空气半球的交界平面上，回线中心与坐标原点重合。由于计算区域有限，为了避免截断效应，将圆球的外围划分出300 m厚的区域作为无限元域。经过网格剖分后，共计54 158个网格域单元。其中，内圆球部分选择自由四面体网格；外圆球部分为无限元域。无限元域的网格剖分选择扫掠方式，网格设置为棱柱，这些棱柱单元以内圆球的三角面为辐射源面。为了保证精度，在发射源和接收点部分进行了网格加密，如图1(b)所示。这种局部加密是保证精度和提高计算效率的一种平衡实施方式。发射电流为下阶跃电流，时间步选择非均匀对数定义方法，观测时间为(1～10 000)×10s。其中，在(1～100)×10s内每十倍频率步数为10，在(1～10)×10s内每十倍频率步数为50，在(1～10)×10s内每十倍频率步数为100。这种非均匀的时间步长设置能够保证数值精度和计算效率。时间步进方法采用向后差分方式，案例总耗时约为11 min。

图1 均匀半空间三维正演模型和网格剖分示意图Fig.1 Schematic Views of Homogenous Half-space 3D Forward Model and Mesh Generation

图2(a)为均匀半空间模型上矩形回线源中心点处磁场分量()时域有限元解与解析解对比。

图2 均匀半空间模型上矩形回线源磁场z分量响应Fig.2 Magnetic Responses of z Component of Rectangular Loop Source over Homogenous Half-space Model

从图2(a)可以看出，有限元解与解析解完全重合。图2(b)为有限元解与解析解的相对误差，整个观测时间范围内相对误差均小于2%，由于在(1～100)×10s内有充足的时间采样，其相对误差小于0.5%。

以含块状高导异常体的三维大地模型进一步验证瞬变电磁三维正演的有效性。如图3(a)所示，该地电模型将电导率为2.0 S·m的块状高导异常体埋于电导率为0.1 S·m的均匀半空间模型中，块状体顶部距离地面30 m，其长、宽、高分别为100、40、30 m，空气电导率设置为1.0×10S·m。矩形发射回线尺寸为100 m×100 m，测点位于回线中心，电流为1 A。该模型最早由Newman等利用积分方程法实施三维正演时引入。计算区域和网格剖分设置与均匀半空间模型案例一致。球形计算区域外围也包含了300 m厚的无限元域，整个计算区域被划分为62 696个网格域单元，其中发射回线与接收点处进行了网格加密，对块状高导异常体也进行了局部网格加密。图3(b)对比了本文的有限元解、Newman等的积分方程解、Wang等的时域有限差分(FDTD)解、Li等的有限元解。在(1～10)×10s内，本文的有限元解与积分方程解、其他有限元解吻合较好，比时域有限差分解略小；在(1～10)×10s内，本文的有限元解与时域有限差分解、其他有限元解吻合较好，比积分方程解略大。需要说明的是，由于积分方程解、时域有限差分解、其他有限元解都是直接从这些研究学者的文章中读取，其精度低于原始计算的数值解，所以没有计算本研究与这些数值解的相对误差。

图3 含块状高导异常体大地模型及其响应曲线Fig.3 Geodetic Model with Massive High Conductive Anomaly and Its Response Curve

3 源外不同地形对电磁响应的影响特征分析

本节考察矩形回线源外不同地形对电磁响应的影响规律。所有案例中，回线源均保持位置、形状、发射电流不变。案例总体上分成两种情况：不含异常体和含异常体。其中，不含异常体情况下，地形存在山脊、山谷两种起伏地形，将地形设置在回线源外的不同距离处；在大地电导率不变的条件下，分别考察不同距离时山脊、山谷地形对电磁响应的影响规律；在距离相同的条件下，考察不同大地电导率时山脊地形对电磁响应的影响规律。含异常体情况下，起伏地形为山脊地形，与发射源保持固定距离，发射源下方一定埋深处存在异常体，考察异常体电导率不同时山脊地形对电磁响应的影响规律。

3.1 不含异常体情况

3.1.1 不同参数下山脊地形对电磁响应的影响

图4为回线源外存在山脊地形的模型示意图。该模型采用100 m×100 m矩形回线源，源中心与坐标原点重合，回线源中心点在坐标原点，在回线源外采用六面体模拟出山脊地形；该六面体上、下表面分别为200 m×200 m和400 m×400 m的矩形，其中心在=0平面上投影重合在轴上，上表面与地面的距离为100 m；空气和大地电导率分别设置为1.0×10S·m和0.01 S·m。如图4(b)所示，将发射回线右棱边与山脊地形最左边棱边的距离设置为可变，考察距离分别为10、50、100、200 m处山脊地形对电磁响应的影响。整个计算区域为半径5 km的圆球，在地面上沿着轴从点(0，-25，0)到点(0，25，0)均匀铺设52个接收点，时域响应的观测范围为(1～10 000)×10s，分别计算出均匀半空间模型、山脊地形模型的接收点处时域磁场分量响应。以均匀半空间模型的数值解为参考，计算存在山脊地形模型磁场响应的相对误差。

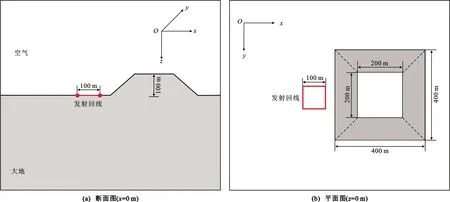
图4 回线源外存在山脊地形的模型示意图Fig.4 Schematic Views of Model Containing a Ridge Topography Outside the Rectangular Loop Source

图5为不同距离处存在山脊地形的时域数值(TDEM)解关于均匀半空间模型的相对误差分布。纵轴为已转换成log域的时间()点，实际范围为(1～10 000)×10s，横轴为轴上接收点的距离。从图5可以看出，误差较大区域集中在某个时间段内，接收点越靠近山脊地形，其相对误差越大，随着距山脊地形的距离不断增大，整体误差水平降低，误差较大区域逐渐移至更晚时间上。这种误差分布的形态主要与电磁波信号的穿透特性有关，发射源发射下阶跃电流后，形成非常宽频带的激励，引起地下介质的感应涡流。频率较高的电磁信号穿透距离较浅；频率较低的电磁信号穿透距离更远。频率较高的电磁信号引起近距离地下介质的感应涡流，该感应涡流形成的二次场在较早时间上回到观测点；频率较低的电磁信号引起远距离地下介质的感应涡流，该感应涡流形成的二次场在较晚时间上回到观测点。接收时间越早，包含的频率成分越高；接收时间越晚，包含的频率成分越低。当山脊地形处于不同距离时，引起感应涡流的电磁波频率成分不同，因此，距离越远，误差较大区域在时间上更晚。同时，山脊地形相对频率较高电磁波的电尺寸更大，因而近距离时山脊地形造成的影响也更大一些。从整体误差水平来看，与发射源距离10 m的山脊地形引起的相对误差高达14%左右，对实际勘探的影响较大；随着山脊地形与发射源的距离增大，误差逐渐减小，距离200 m的山脊地形引起的相对误差小于2%，对实际勘探的影响可以忽略。因此，在实际勘探中，将发射源尽量远离山脊能够减小地形影响。

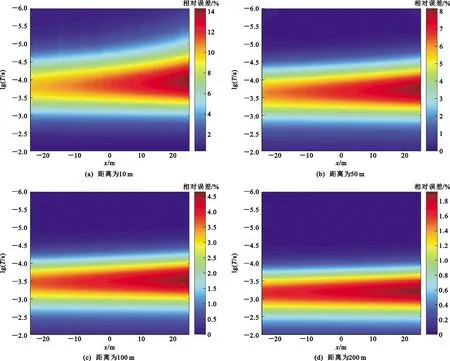
图5 不同距离处存在山脊地形的时域数值解关于均匀半空间模型的相对误差分布Fig.5 Distributions of Relative Errors of TDEM Response of the Model Containing Ridge Topography at Different Distances with Respect to Homogeneous Half-space Model

图6为不同大地电导率时存在山脊地形的时域数值解关于均匀半空间模型的相对误差分布。该山脊地形固定在距离发射源100 m处，整个大地电导率依次设置为0.001、0.005、0.050、0.100 S·m。从图6可以看出，不同大地电导率的整体误差水平基本一致，误差较大区域集中在某个时间段内，接收点越靠近山脊地形，其相对误差越大，随着大地电导率的增大，误差中心逐渐移至更晚时间上。这种误差分布形态也是与电磁波信号的穿透特性有关，电磁波在导电媒质中的传播距离与频率、电导率有关；根据趋肤深度计算公式，当电磁信号频率固定不变时，媒质的电导率越高，电磁能量衰减越快，穿透深度也越浅。因此，对于某一固定距离的山脊地形，当大地电导率增大时，频率更低的电磁信号才能传播到此处，进而引起山脊地形的感应涡流，感应涡流形成的二次场将在更晚时间上回到观测点。从整体误差水平来看，不同大地电导率在不同时间段上引起的误差水平相近，传播到山脊地形的频率成分所覆盖的区域大致相当。因此，在接收点处，山脊区域的贡献也是相对固定的。综上所述，对于固定距离的山脊地形，大地电导率的改变主要影响山脊地形的电磁响应时间；相对均匀半空间模型，山脊地形引起的误差水平基本一致；大地电导率越高，山脊地形引起的误差分布在时间上越晚。

图6 不同大地电导率时存在山脊地形(距离为100 m)的时域数值解关于均匀半空间模型的相对误差分布Fig.6 Distributions of Relative Errors of TDEM Response of the Model Containing Ridge Topography (Distance of 100 m) at Different Conductivities of Earth with Respect to Homogeneous Half-space Model

3.1.2 不同参数下山谷地形对电磁响应的影响

图7为回线源外存在山谷地形的模型示意图。该模型采用100 m×100 m矩形回线源，源中心与坐标原点重合，回线源中心点在坐标原点，在回线源外采用六面体模拟出山谷地形；该六面体上、下表面分别为400 m×400 m和200 m×200 m的矩形，其中心在=0平面上投影重合在轴上，下表面与地面的距离为100 m；空气和大地电导率分别设置为1.0×10、0.01 S·m。如图7(b)所示，将发射回线右棱边与山谷地形最左边棱边的距离设置为可变，考察距离分别为10、50、100、200 m处存在山谷地形对电磁响应的影响。与图4存在山脊地形的模型示意图相比，山谷地形与山脊地形的几何结构是关于地平面对称的，其他参数设置都是相同的，这样的模型设定是为了更好地对比不同类型(凹陷、凸起)地形的影响。

图7 回线源外存在山谷地形的模型示意图Fig.7 Schematic Views of Model Containing a Valley Topography Outside the Rectangular Loop Source

图8为不同距离处存在山谷地形的时域数值解关于均匀半空间模型的相对误差分布。纵轴为已转换成log域的时间点，实际范围为(1～10 000)×10s，横轴为轴上接收点的距离。从图8可以看出，较大误差形成的区域也是集中在一定时间段内，接收点越靠近山谷地型，其相对误差越大，随着距山谷地形的距离不断增大，整体误差水平降低，较大误差区域逐渐移至更晚时间上，距离上靠近山谷地形的误差区域呈现减小趋势。与山脊地形的时域数值解相对误差分布(图5)相比，山谷地形的时域数值解相对误差分布形态与山脊地形呈现相似的特点，引起这种误差分布形态的原因也是一样的。不同的是，山谷地形引起的误差水平更高，与发射源距离10 m的山谷地形引起的相对误差高达25%左右，而同等距离山脊地形引起的相对误差为14%左右，可见山谷地形比山脊地形对实际勘探的影响更大；随着山谷地形与发射源的距离增大，相对误差逐渐减小，距离为200 m的山谷地形引起的相对误差小于4%。因此，为了减小地形对电磁响应的影响，有效措施依然是尽量远离山谷地形。

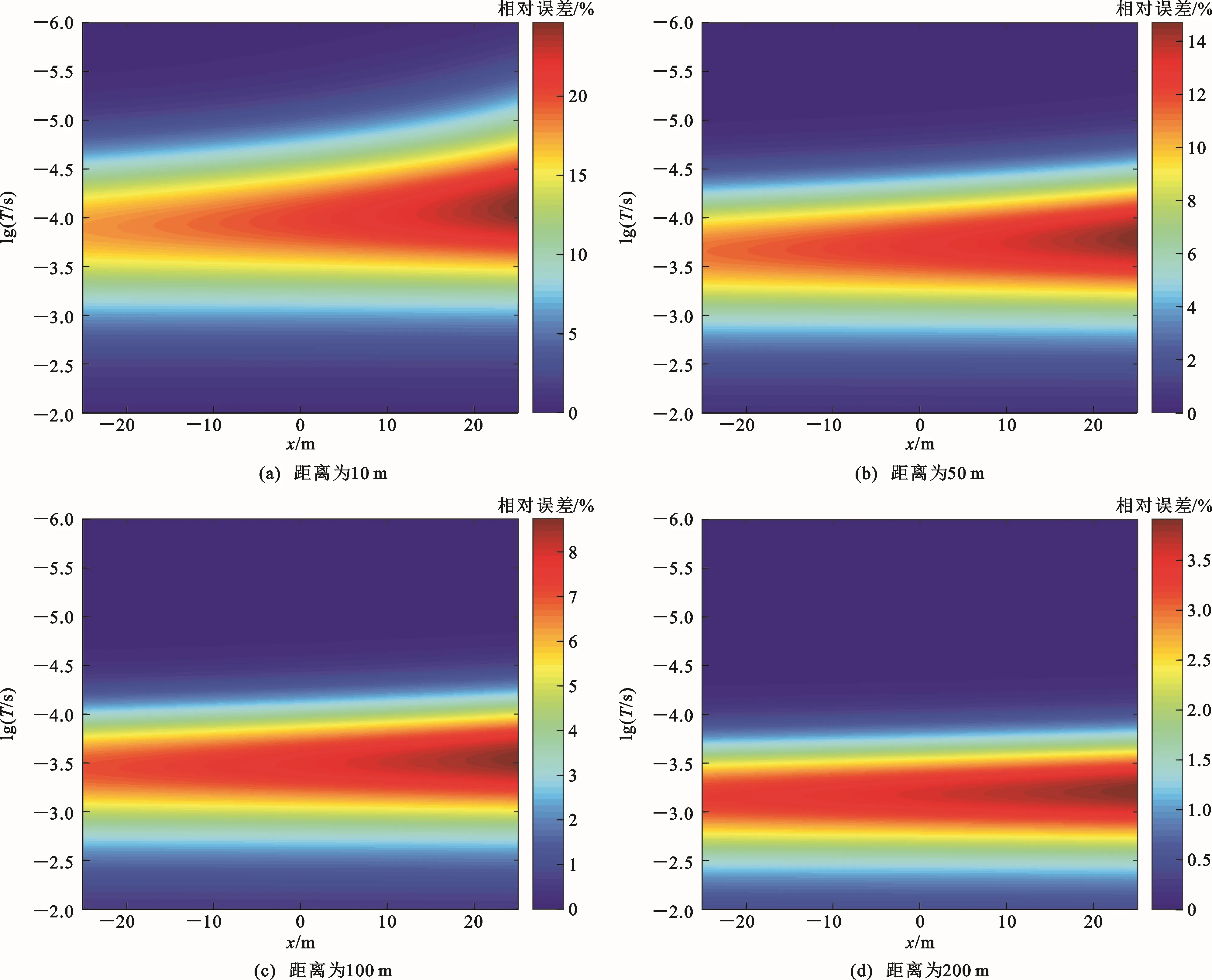
图8 不同距离处存在山谷地形的时域数值解关于均匀半空间模型的相对误差分布Fig.8 Distributions of Relative Errors of TDEM Response of the Model Containing Valley Topography at Different Distances with Respect to Homogeneous Half-space Model

3.1.3 不同距离下两种地形的时间域电磁响应

以均匀半空间模型的电磁响应作为参考，考察不同距离下山脊、山谷地形的时间域电磁响应(图9)。从图9(a)可以看出，山脊地形的贡献是增大一定时间段的电磁响应。根据前文分析，发射源引起地下导电介质的感应涡流，感应涡流产生二次场，然后观测点处接收该二次场；与均匀半空间模型相比，山脊地形相当于延展了一部分导电介质区域，增加了一定的感应涡流，导致产生了更强的二次场。从图9(b)可以看出，山谷地形的影响是减小一定时间段的电磁响应。与均匀半空间模型相比，山谷地形相当于减小了一部分导电介质区域，缺少了部分区域的感应涡流，导致二次场比均匀半空间模型更弱。

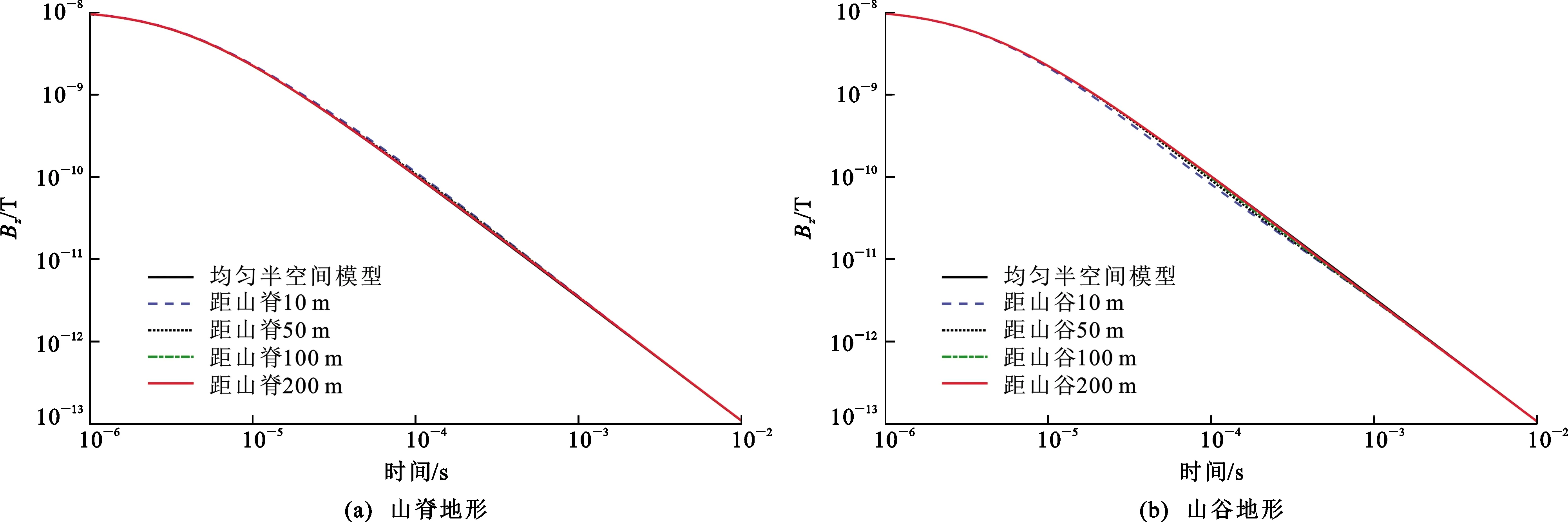
图9 两种地形在中心点处的时域数值解Fig.9 TDEM Responses at the Central Receiving Point for Two Kinds of Topography

3.2 含异常体情况

图10为含异常体与山脊地形的模型示意图。矩形回线源的参数和山脊地形的几何尺寸与3.1.1节一致。如图10(b)所示，将发射回线右棱边与山脊地形最左边棱边的距离设置为100 m。异常体的顶部埋深为50 m，长为100 m，宽为200 m，高为40 m，其中心在=0平面上投影为坐标原点。在本节所有案例中，异常体的几何信息不变，其电导率是可变的，以考察不同电导率异常体对电磁响应的影响。计算区域与网格剖分的参数与前面案例一致。在地面上沿着轴从点(0，-25，0)到点(0，25，0)均匀铺设52个接收点，分别计算出均匀半空间模型、异常体(不含地形)模型、异常体(含地形)模型这3种情况下接收点处时域磁场分量响应。

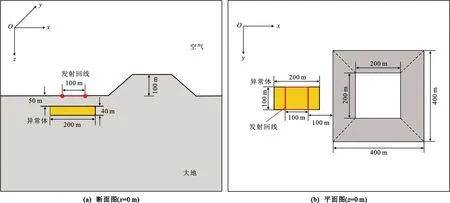
图10 含异常体与山脊地形的模型示意图Fig.10 Schematic Views of Model Containing Ridge Topography and Anomaly

3.2.1 异常体(不含地形)模型

以均匀半空间模型的数值解为参考，计算异常体(不含地形)模型关于均匀半空间模型磁场响应的相对误差，以考察不同电导率异常体对电磁响应的影响。异常体电导率依次设定为1.00、0.50、0.10、0.05 S·m。图11为不同电导率异常体(不含地形)模型的时域数值解关于均匀半空间模型的相对误差分布。从图11可以看出，不同电导率异常体对电磁响应的影响主要集中在一定的时间段内，随着异常体电导率的减小，异常体引起的误差水平逐渐降低，同时误差中心区域在时间上逐渐移至更早期。如3.1节的案例分析一样，异常体引起的误差分布形态主要与电磁波信号的穿透特性、感应涡流有关。异常体电导率越高，不仅能够产生更强的二次场响应，同时二次场在接收时间上的影响持续时间越长，其最大影响中心在时间上也越晚。

图11 不同电导率异常体(不含地形)模的时域数值解关于均匀半空间模型的相对误差分布Fig.11 Distributions of Relative Errors of TDEM Response of the Model Containing Anomaly (Without Topography) at Different Conductivities with Respect to Homogeneous Half-space Model

为了更好地理解不同电导率异常体对电磁响应的影响，本文给出了在回线源中心处不同电导率异常体(不含地形)模型的时间域磁场分量响应(图12)。从图12可以看出：不同电导率异常体磁场响应逐渐增强的起始时间是一致的，这是由于异常体的位置是固定的，电磁信号传播到不同电导率异常体所经历的导电媒质和距离是不变的；同时，可以观察到异常体的贡献是增大一定时间段内的电磁响应，电导率越高，其二次场响应增大的幅度越高，持续时间越长。

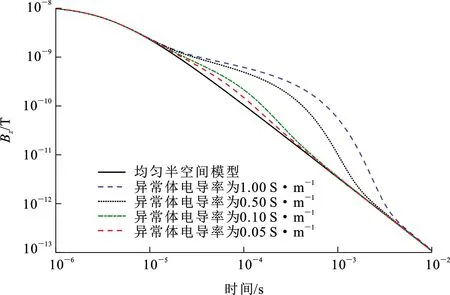
图12 不同电导率异常体(不含地形)模型在中心点处时域数值解Fig.12 TDEM Responses at the Central Receiving Point for Models with Anomaly (Without Topography) at Different Conductivities

3.2.2 异常体(含地形)模型

本文计算了同时包含异常体和地形模型的时域数值解，然后分别以均匀半空间模型、异常体(不含地形)模型的数值解为参考，计算了异常体(含地形)模型分别关于这两种模型的磁场响应的相对误差。其中，异常体电导率依次设定为0.10、0.05 S·m。图13为不同电导率异常体(含地形)模型的时域数值解关于均匀半空间模型的相对误差分布。与图11(c)、(d)不含地形的情况相比，图13整体误差水平与分布形态基本一致，难以分辨地形的影响特征。因此，为了单独观察地形对电磁响应的影响，图14给出了不同电导率异常体(含地形)模型的时域数值解关于异常体(不含地形)模型的相对误差分布。当异常体电导率不同时，图14的误差分布形态和水平基本一致，这也与图5(c)的结论基本一致。这说明地形、异常体对电磁响应的影响可以分离。对于一个包含地形效应的实测数据，如果异常体产生的二次场比较强，地形效应的影响相对非常小，可以忽略，将地面当作理想平面来处理数据；如果异常体产生的二次场较弱，则不能忽略地形效应的影响，此时如将地面当作理想平面来处理数据，则异常体电导率的反演值与真实值差距较大；如果地形效应比较强，例如起伏地形比较靠近发射源，不考虑地形去反演数据，也容易将地形效应产生的二次场差异当作是异常体。

图13 不同电导率异常体(含地形)模型的时域数值解关于均匀半空间模型的相对误差分布Fig.13 Distributions of Relative Errors of TDEM Response of the Model Containing Anomaly (with Topography) at Different Conductivities with Respect to Homogeneous Half-space Model

图14 不同电导率异常体(含地形)模型的时域数值解关于异常体(不含地形)模型的相对误差分布Fig.14 Distributions of Relative Errors of TDEM Response of the Model Containing Anomaly (with Topography) at Different Conductivities with Respect to the Model Containing Anomaly (Without Topography)

4 结 语

本文针对地面电磁勘探法，不考虑发射源形变，构建了矩形回线源外存在不同地形的多种勘探场景，基于有限元法计算了不同场景下的电磁响应，考察了地形、电性等参数变化对瞬变电磁响应的影响规律。

(1)源外地形对电磁响应的影响主要集中在某个时间段内，越靠近地形的观测点，受影响程度越严重；随着与发射源距离增大，地形作用减弱，受影响区域也推移到较晚期时间段上。

(2)当地形与发射源的距离不变时，随着大地电导率增大，地形主要影响区域趋向于集中在更晚期时间上，但是受影响的程度基本一致。

(3)相同几何尺寸的山谷地形比山脊地形对电磁响应的影响更大。山谷地形对电磁响应的影响是减小某个时间段内二次场响应，而山脊地形则是增强一定时间段内二次场响应。

(4)地形、异常体对电磁响应的影响可以分离，异常体的变化并不会增强或减弱地形对电磁响应的贡献。对于包含地形效应的勘探数据，如果异常体产生的二次场比较强，地形效应的影响相对较小，可以忽略地形；如果异常体产生的二次场较弱，则不能忽略地形效应的影响。

谨以拙作祝贺西安地质调查中心组建六十周年！西安地质调查中心一直承担着国家在西北地区的基础性、公益性地质调查和战略性矿产勘查任务及相关综合研究工作，取得了丰硕的研究成果和荣誉。西安石油大学与西安地质调查中心多年来在油气成藏地质学、非常规油气地质与勘探、深部地质构造、含油气盆地构造学、油气田开发地质学及地震勘探等多个领域进行了深入合作，形成了良好的合作关系。作为西安石油大学的一份子，期待未来参与到西安石油大学和西安地质调查中心进一步的合作中，携手为国家能源安全和可持续发展做出新的贡献！