基于约束连接方向的最速上升法提取山脊线

邓晓龙， 江文萍， 孙二洋， 张 萍， 于 池

(武汉大学 资源与环境科学学院， 武汉 430079)



邓晓龙， 江文萍*， 孙二洋， 张 萍， 于 池

(武汉大学 资源与环境科学学院， 武汉 430079)

对基于格网DEM提取山脊线的方法进行了研究，针对基于格网DEM的流水物理模拟法和最速上升法提取山脊线所存在的问题，提出了基于约束连接方向最速上升法.该方法将山顶点和鞍部点作为控制点、以约束山脊线的连接方向来达到改善山脊线提取效果的目的.减少了山脊线断裂、交叉和回转等错误现象，同时提取的山脊线主次分明层次性良好，与实际地形相符合.

格网DEM; 山脊线; 约束连接方向; 流水物理模拟法; 最速上升法

地性特征线是地貌形态的骨架线，是数字形式描述和处理地貌时的控制线，它主要包括山脊线、山谷线，山脊线的自动提取在水文分析、高质量DEM生成、制图综合、土壤侵蚀分析、遥感数字图像处理以及解析地貌等方面均有着十分重要的作用[1-2].由于格网DEM获取方法的广泛性和数据精度不断提高的特性，基于格网DEM自动提取地性特征线的方法被普遍使用和研究[1].基于规则格网DEM数据的山脊线提取方法从算法设计原理上可以分为以下两种：基于地形表面几何形态分析方法[3]和基于地形表面流水物理模拟方法[4].

基于地形表面形态分析方法主要是考虑点与其领域内其他点高程之间的关系来确定该点的特征类型[3]，该方法简单易于实现，但是容易把不是特征点的点误判为特征点[5].许多学者对该算法进行改进，但是都不能彻底解决该问题[6-7].此外，最速上升法提取山脊线的算法复杂度低且易于实现，在单独山顶点情况下该方法提取的山脊线与实际地形符合良好[8]，而且该方法有效地改善了应用比较广泛的离散拉普拉斯算法(D.L.T)[9]在提取山脊线时发生的粘连的情况.但是最速上升法在多山顶点和鞍部点且交替连续出现的情况该方法考虑不足，提取山脊线在山顶点处可能发生断裂，使得主要的山脊线发生断裂不连续，而且该方法提取山脊线时没有考虑与山谷线相交的可能性.

基于规则格网DEM的流水物理模拟算法自1984年提出就被广泛的研究和应用[10-11]，该方法首先要对格网DEM进行填平洼地和确定平地区域流水方向的数据预处理.有许多改善洼地处理效果的算法，但是如何确定平地区域的流水方向一直是该方法的难题[12-13]，如果格网数据量比较大且洼地、平地比较多，则该方法提取地性特征线的算法复杂度与时间复杂度都比较高[14-15].流水物理模拟法提取山脊线有两种办法[10]：一是将DEM高程矩阵整体反转，进行洼地和平地的预处理，然后提取出的特征线就是山脊线(分水线)，但是该方法同样面临着洼地处理与平地流向难确定的问题；二是从分水岭中提取山脊线，但是如何连接分水岭离散点成山脊线是主要难题，因为这些分水岭的点只有流出的流向没有流入的流向，所以不能像流水物理模拟法提取山谷线时按照流向连接特征线[16]. 针对最速上升法和流水物理模拟法提取山脊线存在的问题，本文对基于控制点的山脊线提取方法进行了研究.

1 基于约束连接方向的最速上升法

1.1 提取主要山脊线

1.1.1 建立坐标系 汇水流量矩阵中汇水流量值等于零的格网单元为分水岭离散点，本模型采用了简单且容易实现的方法从这些分水岭离散点中提取山顶点和鞍部点[17]，依次以离散点为中心建立3×3的窗口，如果窗口中心点的高程比其周围的八邻域的高程都大则该中心点为山顶点，图1中Pc2和Pc5所示的点为山顶点；如果中心点两个相互正交的方向上，一个方向为凹陷，另一个为凸起，则该中心点为鞍部点，图1中Pc3所代表的是鞍部点.接下来通过离散的分水岭的点连接山顶点，连接山顶点时首先以该山顶点为原点建立二维X、Y坐标系如图2所示，该坐标系分为第一象限、第二象限、第三象限、第四象限、X正半轴、Y正半轴、X负半轴和Y负半轴8个区域，坐标系的8个区域分别对应八个山顶点队列.把其余山顶点根据其在该坐标系中的位置依次添加到相应区域的山顶点队列中，并按照山顶点到原点的距离从小到大的顺序排序每个队列中的山顶点.

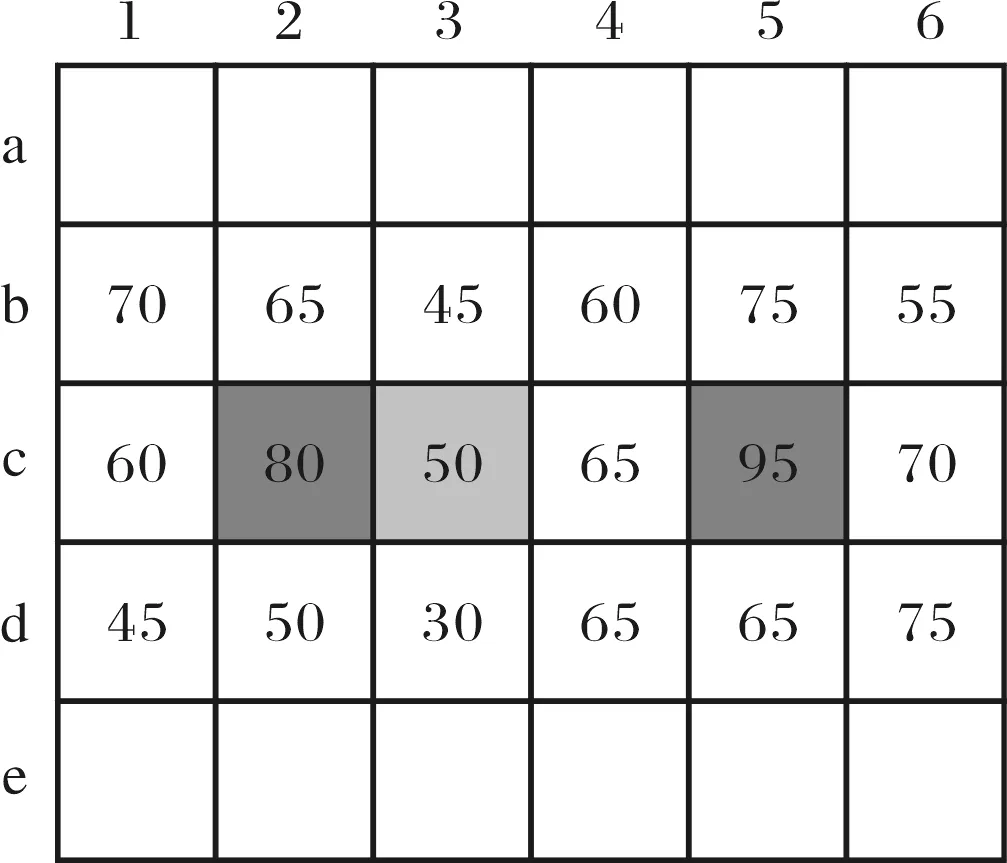
图1 山顶点和鞍部点Fig.1 Hill and saddle points

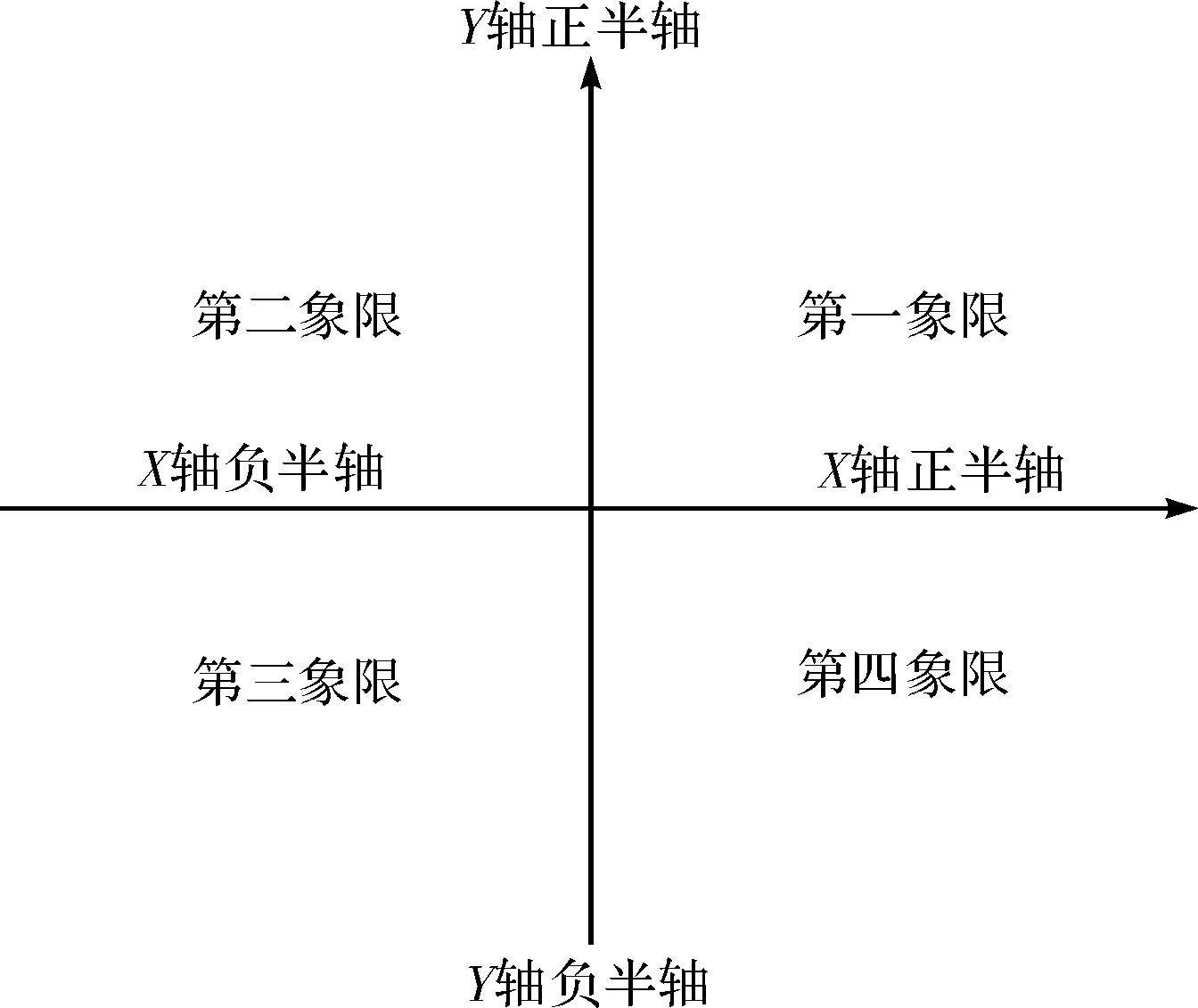
图2 山顶点的坐标系Fig.2 Coordinate system of hill point

本模型把8个区域队列中要连接的山顶点定义为“终止山顶点”，原点处的山顶点为“起始山顶点”，连接过程中山脊线最后一个山脊点为“连接山脊点”.依次从8个区域的山顶点队列中取出一个山顶点，先判断取出的山顶点与“起始山顶点”是否连接，如果连接过则取出山顶点队列中下一个进行判断，否则创建存储连接山脊线的点数组，并把起始山顶点加入到山脊线点数组中.取出山脊线点数组中最后一个山脊点为“连接山脊点”，如果该“连接山脊点”为“终止山顶点”则结束了一条山脊线的连接，否则以该“连接山脊点”为原点建立二维的X、Y坐标系，并划分为16个区域如图3所示.然后计算“终止山顶点”在连接山脊点坐标系中的位置.

图3 连接山脊点的坐标系Fig.3 Coordinate system of connection point

图4 连接点的八邻域Fig.4 Eight neighborhoods

1.1.2 建立连接优先级 “连接山脊点”的八邻域如图4所示，“连接山脊点”八邻域内一般都会有多个可以连接的分水岭离散点.本文定义了这些八邻域内的分水岭离散点添加到山脊线的优先级为Priority，并用Px表示‘X’点的优先级.在连接山脊线时本模型实时计算山脊线最后一个连接点与“终止山顶点”的位置关系，根据 “终止山顶点”在连接山脊点坐标系中的位置来确定连接的山脊线的大致走向，本模型用山脊线最后一个连接点指向“终止山顶点”的方向向量表示山脊线的大致走向.接下来分别计算连接点指向其八领域内的分水岭离散点的方向向量，分水岭离散点的方向向量与山脊线大致走向的夹角和优先级成反比，夹角越小则优先级越大，夹角越大则优先级越小，如果夹角相等则优先级相等.根据优先级从大到小的顺序判断下一个可能的山脊线连接点，当两个连接点的优先级相等则高程值大优先加入到连接山脊线的点数组中.在连接任意一条山脊线的过程中不考虑已经加入山脊线的分水岭离散点，这样可以有效地避免山脊线发生回转、与自身交叉等错误现象.“终止山顶点”在坐标系中16个区域所对应的下一个连接点可能位置和其优先级汇总表如表1所示.

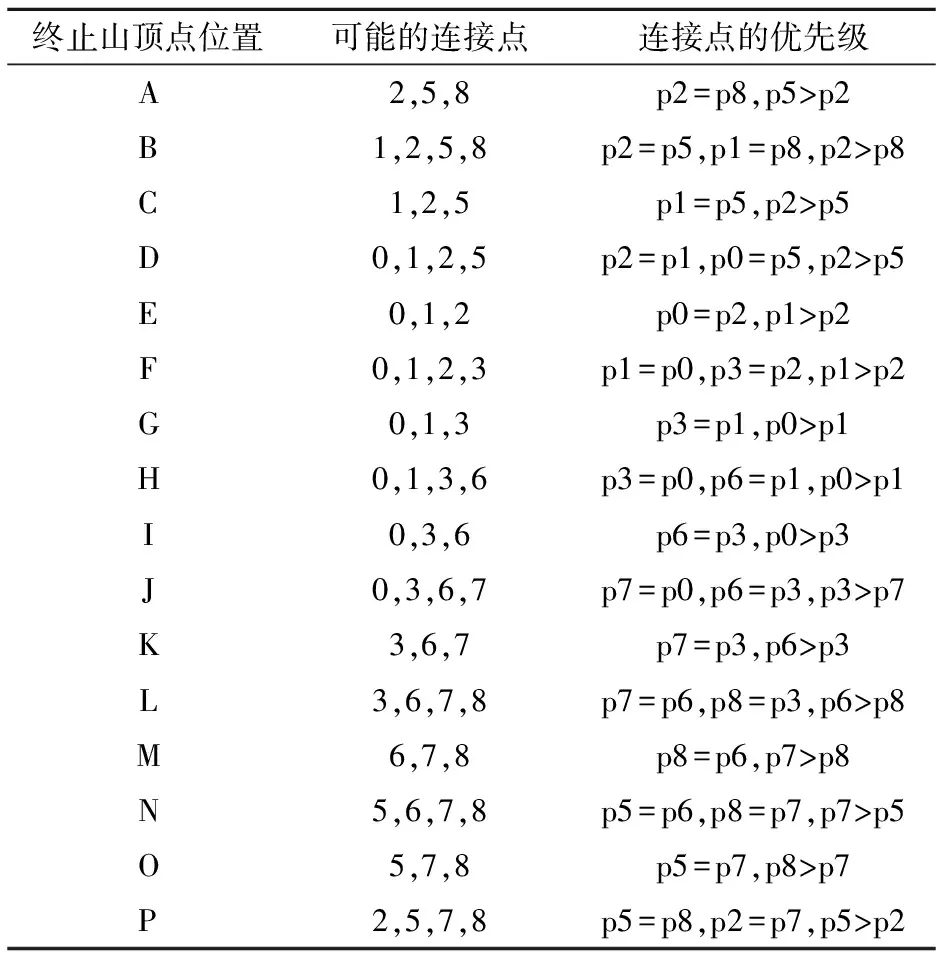
表1 山脊线连接点的优先级汇总表

1.1.3 连接鞍部点 经过上述步骤之后大部分鞍部点在山顶点连接过程中都被连接起来，如果有鞍部点没有连接过则把该鞍部点为原点建立如图2所示的坐标系，因为鞍部点的特点：在某一方向上在鞍部点的两边往往存在着两个山顶点.本模型分别计算出鞍部点坐标系中16个区域内距离原点最近的山顶点，并选择两个不在同一个区域且离鞍部点最近的山顶点，以该鞍部点为起始点分别向两个山顶点方向连接，连接方法与上述的连接山顶点方法类似，通过建立的分水岭离散点的优先级队列来判断连接的下一个山脊点，如果连接过程中遇到山顶点或则与其他山脊线相交则结束连接.连接结束后一般会有两条山脊线，这两条山脊线有着相同的起点即没有连接过的鞍部点，把这两条山脊线合并成一条山脊线.

1.2 次要山脊线的提取

在连接次要的山脊线之前需要对已经连接的主要山脊线和所有的分水岭离散点进行如下处理：连接成主要山脊线的分水岭离散点设置为连接过标志，连接主要山脊线过程中遍历的离散点设置为检测过标志.在剩余的分水岭离散点中查找没有连接过和检测过且高程值最小的开始连接次要山脊线，连接每一条山脊线时根据连接山脊线点数组中最后两个连接点来约束连接方向.图5中表示了山脊线最后两个连接点在八邻域内的具体情况，其中BP表示前一个连接点，EP表示最后一个连接点，深色区域表示该处的点已经被排除，连接的时候不予考虑，因为这些连接点可能导致山脊线发生回转和交叉.在连接点的八邻域内查看浅色区域位置上的连接点，找出其中高程值最大且要大于最后连接点的离散点，如果该点没有连接过和没有检测过则直接加到连接山脊线点数组中继续进行连接；如果该点连接过则加入到连接山脊线点数组中并且结束这条山脊线的连接开始下一条山脊线的连接；如果该点检测过则要判断该点八邻域内是否存在连接过的山脊点，如果存在则把该点和连接过的山脊点依次加入到连接点数组中并结束连接，如果不存在则结束山脊线的连接.

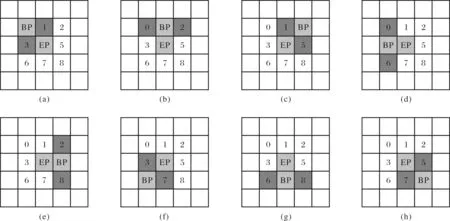
图5 次要山脊线的最后两个点约束连接方向Fig.5 Automatic constraint connecting direction

2 实验与分析

2.1 实验过程与数据

本模型的实验环境是Windows系统和VS2010，算法采用C++编写，在本模型的算法中定义了若干变量，其中DemMatrix为原始DEM矩阵，DemMatrixPre是经过洼地平地处理和计算了汇水流量的DEM矩阵，HillSaddleArray是存在于DemMatrixPre中的山顶点和鞍部点，MajorRidgeArray是在山顶点和鞍部点约束下连接的主要山脊线，MiniorRidgeArray是在山脊线最后两个点约束下连接的次要山脊线.本模型算法主要分为原始DEM数据的预处理、山顶点和鞍部点、连接主要山脊线和连接次要山脊线，伪代码如下所示：

① DemMatrixPre=PretreatDemdata(DemMatrix);

② HillSaddleArray=LocateHillSaddle(DemMatrixPre);

③ MajorRidgeArray=ConnectMajorridge(HillSaddleArray);

④ MiniorRidgeArray=ConnectMiniorridge();

本次实验数据是从SRTM网站上下载的90 m的格网DEM数据，提取山脊线的实验区域为左上经纬度是(100.85°E，30.18°N)右下经纬度是(100.99°E，30.04°N)的正方形区域，该区域位于四川西南部，最大高程为4 665 m,最小高程为2 640 m，地形起伏明显.

2.2 对比与分析

采用流水物理模拟法提取山脊线时如何连接分水岭离散点比较困难，因为这些分水岭离散点只有流出的流向没有流入的流向，所以不能像连接山谷线那样按照流向来连接.此外最速上升法算法简单且容易实现，该算法是从没有连接过的且高程值最小的山脊点开始连接，查看连接点的八邻域高程值并找出高程值最大的点，如果该高程值最大的点没有连接过且高程大于连接点，则把该点加入到连接的山脊线中，否则结束连接.但是山顶点的高程值大于其八邻域内点的高程值，所以最速上升法连接山脊线的过程遇到山顶点必然发生断裂，这不仅导致主要山脊线没有连接起来，而且影响后续的山脊线之间连接处理.

为了解决分水岭不容易连接成山脊线和最速上升法提取山脊线容易发生断裂的问题，本文是先从分水岭的离散点中确定山顶点和鞍部点如图6(a)所示，其中三角形的点为山顶点圆形的点为鞍部点，在山顶点和鞍部点的连接方向的控制下连接分水岭的离散的点成主要的山脊线如图6(b)所示，剩余的分水岭的离散点通过改进的最速上升法连接，最后对次要山脊线进行删除短小山脊线和连接到主要山脊线的处理，其提取结果如图7(a)所示，图7(b)中的山脊线为最速上升法提取的山脊线，从图7(b)可知最速上升法提取的山脊线比较破碎，而且提取的山脊线没有主次之分，主要山脊线和短小的次要山脊线同样宽度.从图7中(a)和(b)的对比可知，本模型提取的山脊线相较最速上升法连续且主要山脊线和次要山脊线在宽度上区别明显，同时通过晕渲图7(a)中的等高线可知本模型提取的山脊线与山脊的走势相符即与实际地形较好的符合.

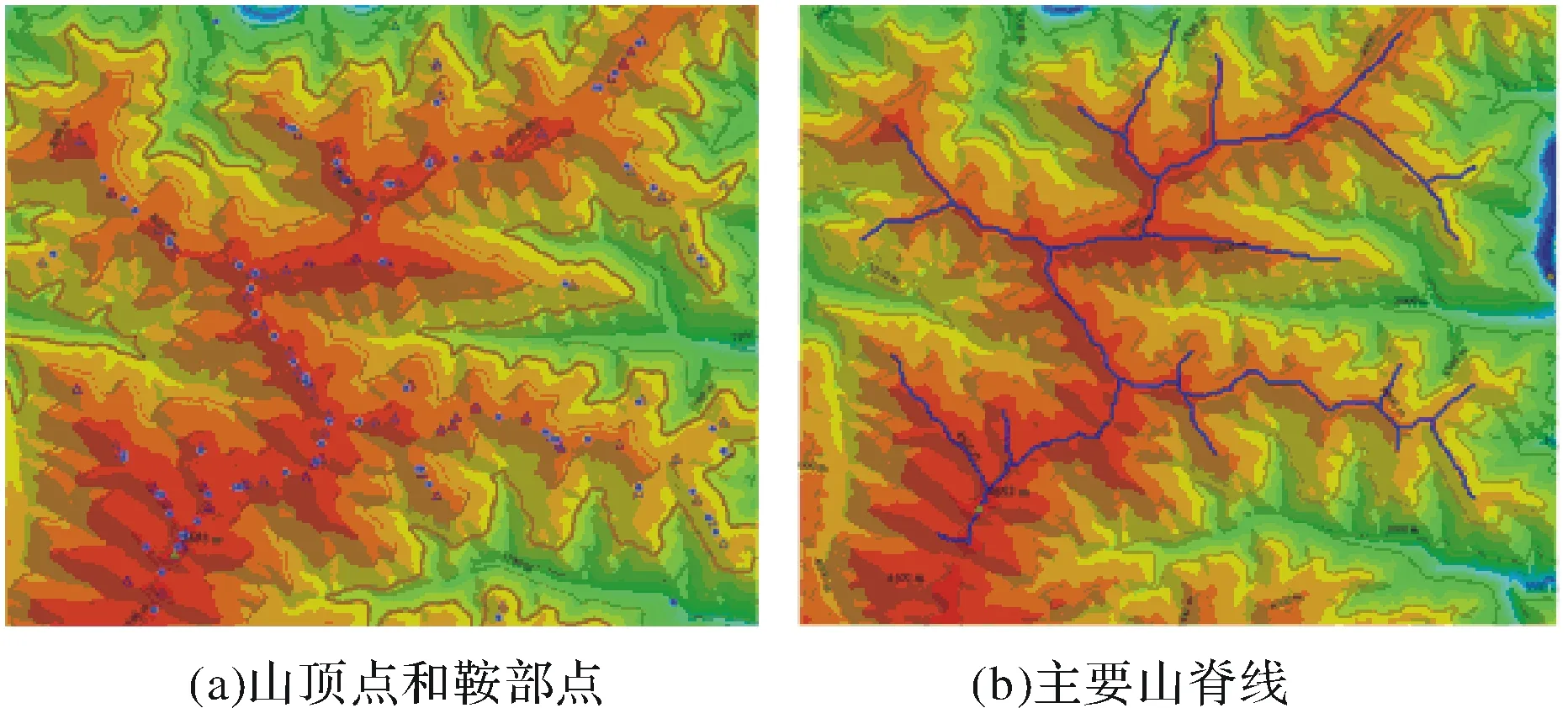
图6 本模型约束连接方向的控制点与提取的主要山脊线Fig.6 Control points and major lines

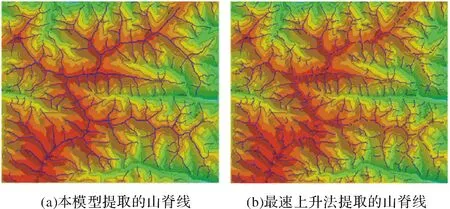
图7 本模型与最速上升法提取山脊线对比图Fig.7 Comparison with steepest ascent method

3 结束语

本文提出的约束连接方向最速上升法提取存在于流水物理模拟法确定的分水岭中的山脊线，通过分水岭中的山顶点、鞍部点和山脊线最后两个点约束山脊线的大致连接方向.与最速上升法提取分水岭中的山脊线相比，本文提取的山脊线在连续性、层次性和整体性都有所提高，同时也解决了流水物理模拟法连接分水岭中的山脊线的难题.

值得注意的是，本文提出的约束连接方向最速上升法也存在很大的改进空间，连接主要山脊线时只通过山顶点和鞍部点约束山脊线的连接方向，控制点不应该仅限于山顶点和鞍部点还需考虑更多的特征点类型，同时在连接主要的山脊线时需要考虑更多的情况.

[1] O’CALLAGHAN J F, MARK D M. The extraction of drainage networks from digital elevation data[J]. Computer vision, graphics, and image processing.1984, 28(3): 323-344．

[2] 罗 伟， 鄢志武， 薛重生. 基于DEM的岩溶地区地形地貌特征提取与分析[J]. 华中师范大学学报(自然科学版). 2013(03): 436-439．

[3] JENSON S K. Automated derivation of hydrologic basin characteristics from digital elevation model data[C]. 1985. 301-310．

[4] JENSON S K, DOMINGUE J O. Extracting topographic structure from digital elevation data for geographic information system analysis[J]. Photogrammetric engineering and remote sensing. 1988, 54(11): 1593-1600．

[5] 郭明武， 吴 凡. 基于规则格网DEM自动提取地性线的一种简便方法[J]. 测绘信息与工程, 2005(2): 33-34．

[6] 黄培之. 提取山脊线和山谷线的一种新方法[J]. 武汉大学学报(信息科学版). 2001(3): 247-252．

[7] YOELI P. Computer-assisted determination of the valley and ridge lines of digital terrain models[J]. International Yearbook of Cartography. 1984, 24: 197-206．

[8] KOKA S, ANADA K, NOMAKI K, et al. Ridge Detection with the Steepest Ascent Method[J]. Procedia Computer Science, 2011, 4: 216-221．

[9] KOKA S, ANADA K, NAKAYAMA Y, et al. A Comparison of Ridge Detection Methods for DEM Data[C]// IEEE, 2012. 513-517．

[10] 朱 庆， 赵 杰， 钟 正， 等. 基于规则格网DEM的地形特征提取算法[J]. 测绘学报, 2004(1): 77-82．

[11] GARBRECHT J, MARTZ L W. The assignment of drainage direction over flat surfaces in raster digital elevation models[J]. Journal of hydrology, 1997, 193(1-4): 204-213．

[12] BAI R, LI T, HUANG Y, et al. An efficient and comprehensive method for drainage network extraction from DEM with billions of pixels using a size-balanced binary search tree[J]. Geomorphology, 2015, 238: 56-67．

[13] ZHANG H, HUANG G. Building channel networks for flat regions in digital elevation models[J]. Hydrological Processes, 2009, 23(20): 2879-2887．

[14] BARNES R, LEHMAN C, MULLA D. An efficient assignment of drainage direction over flat surfaces in raster digital elevation models[J]. Computers & Geosciences, 2014, 62: 128-135．

[15] JANA R, RESHMIDEVI T V, ARUN P S, et al. An enhanced technique in construction of the discrete drainage network from low-resolution spatial database[J]. Computers & geosciences, 2007, 33(6): 717-727．

[16] FREEMAN T G. Calculating catchment area with divergent flow based on a regular grid[J]. Computers & Geosciences, 1991, 17(3): 413-422．

[17] WOOD J. The geomorphological characterisation of digital elevation models[Z]. University of Leicester (United Kingdom), 1996.465-479.

Detecting ridge lines with the constrained connecting direction steepest ascent method

DENG Xiaolong， JIANG Wenping， SUN Eryang， ZHANG Ping， YU Chi

(School of Resource and Environmental Sciences， Wuhan University， Wuhan 430079)

In this paper， methods for extracting ridge lines from grid digital elevation models are studied. To overcome shortcomings of the overland flow simulation method and the steepest ascent method， the constrained connecting direction steepest ascent method is proposed. Hill points and saddle points are defined as control points. Connecting direction is constrained to improve extraction. The results show that the method is effective for decreasing the fragmentation， cross and rotation of extracted ridge lines. Moreover， it has better performance in the continuity and integrity of ridge lines than the two basic methods mentioned above．

Grid DEM; ridge lines; constrained connecting direction; overland flow simulation; steepest ascent method

2015-06-03.

国家自然科学基金(41371428；41201473);国家基础科学人才培养基金(J1103409).

1000-1190(2015)06-0979-05

P283.8; TU198+.5

A

*通讯联系人. E-mail: 0020377@whu.edu.cn.