带有周期性扰流结构的微通道内流动与传热特性
李艺凡,王志鹏
(1 天津城建大学能源与安全工程学院,天津 300384;2 天津蓝天太阳科技有限公司,天津 300384)
随着第5代移动通信技术的发展,微型器件上晶体管的集成密度大幅增加,特征尺寸显著缩小,并开始从传统二维平面向三维发展。微型器件的功耗密度成倍增大,极易出现局部热点。微型器件的温度直接影响工作性能和使用寿命,散热问题已经成为制约其应用的严重障碍,且常规冷却技术无法满足需求。因此,迫切需要研发换热性能优良、温度分布均匀、泵功能耗低的微型散热器,解决信息通信、航空航天、军工核能等高新技术领域中微型器件的散热问题。
微通道热沉自1981年由Tuckerman和Pease提出后就得到了研究者的青睐。然而由于微型器件日益增加的热负荷及严格的温度限制,简单结构的微通道热沉已经不能满足需求。国内外学者通过提高局部对流传热系数或增大传热面积,提高热沉的散热性能,研究工作主要包括:改进微通道布置型式及进出口位置;改进微通道结构。Zhai 等将双层微通道热沉的上、下两层通道交错布置,有效降低了热阻,提高了热沉均温性。Ma等提出了布置两个进口和两个出口的微通道热沉,由于缩短了通道长度,热沉的热阻和压降均显著降低,热沉温度场也更加均匀。一些研究者将植物叶脉分形结构引入微通道,提高了热沉的传热效率,降低了流阻。还有一些研究者在热沉内部加入局部扰流结构,使流体流动方向和速度发生改变,破坏流动和热边界层,从而提高热沉的传热性能,消除局部热点。王晗等对带有周期性分流微结构的热沉进行了数值研究,新型结构能够有效抑制热沉沿流动方向的温升,降低热阻。陈然等在双层微通道中布置金字塔形结构,研究了该结构间距和底高比对流动和传热的影响。结果表明,微结构降低了总热阻,提高了努塞尔数()。陈卓等数值研究了微通道内自由摆动方柱对流体的扰动作用。与固定方柱相比,自由摆动方柱能够更显著地促进流体横向流动,增强热质传递。
Bejan提出熵产率分析流动和传热不可逆损失,从热力学第二定律的角度描述系统的能量利用效率。很多研究者采用该方法评价微通道热沉,分析微结构强化传热的本质,优化热沉结构。Japar 等在微通道局部布置凹穴、针肋、二次通道,显著降低了传热不可逆性,提高了热沉的综合性能。Datta 等利用熵产原理分析了带有凹穴和针肋的微通道内流动和传热不可逆损失,研究了几何结构对总熵产的影响。复杂微结构增强传热的同时会增大流动阻力,导致泵功能耗增大,因此众多学者利用热阻随泵功的变化规律衡量热沉的综合性能。此外,Webb提出了强化传热因子的概念,该参数同时考虑传热的增量和压降的增量,被广泛应用于评价微型热沉的综合性能。
本文作者课题组设计了一种带有周期性扰流结构的微通道热沉,周期性扰流结构由微通道侧壁的凹穴和微通道中间的针肋组成,微结构使流体在层流下产生局部混沌对流,显著增强了传热。与传统矩形通道、仅布置凹穴或仅布置针肋的微通道相比,虽然该结构增大了流阻,但明显提高了热沉的综合性能。随后,研究了凹穴和针肋的形状和宽度对流动和传热的影响,研究表明梯形凹穴和矩形针肋组成的周期性扰流结构能够有效抑制热沉沿流动方向的温升,热沉平均温度最低且均温性最佳。因此,本文以前期研究为基础,进一步对梯形凹穴和矩形针肋组成的周期性扰流结构进行优化,研究梯形凹穴底边长度对热沉性能的影响,旨在进一步提高该类热沉的传热效率,降低压降和泵功,提高综合性能,为该类热沉在高热流微型器件冷却领域的实际应用提供理论指导。
1 物理模型
微通道热沉的基底材料为硅,工质为去离子水。如图1(a)所示,硅基热沉包含10根平行并联的微通道,每根微通道的中间均匀布置矩形针肋,微通道侧壁均匀布置等腰梯形凹穴。相邻两根微通道侧壁上的凹穴交错布置。在玻璃盖板上加工流体进/出口,并将盖板与硅基底键合在一起,组成封闭的微通道热沉。数值模拟时选取最小的对称单元进行计算,从而提高计算效率。硅基热沉整体尺寸、计算区域结构及尺寸如图1(a)所示。图1(b)为周期性扰流结构的局部放大,几何尺寸见表1。其中,梯形底边长度变化范围为0~180μm,梯形底边长与凹穴总长度的比值RL (relative length)的变化范围是0~0.9。

表1 微通道热沉几何尺寸 单位:μm

图1 微通道计算区域及局部几何结构示意图
2 数学模型
在本文参数范围内,微通道内流动均属于稳态、不可压缩、层流流动。流体的动力黏度随温度变化,见表2。其他物性参数及固体的物性参数为常数,与文献[27]一致。
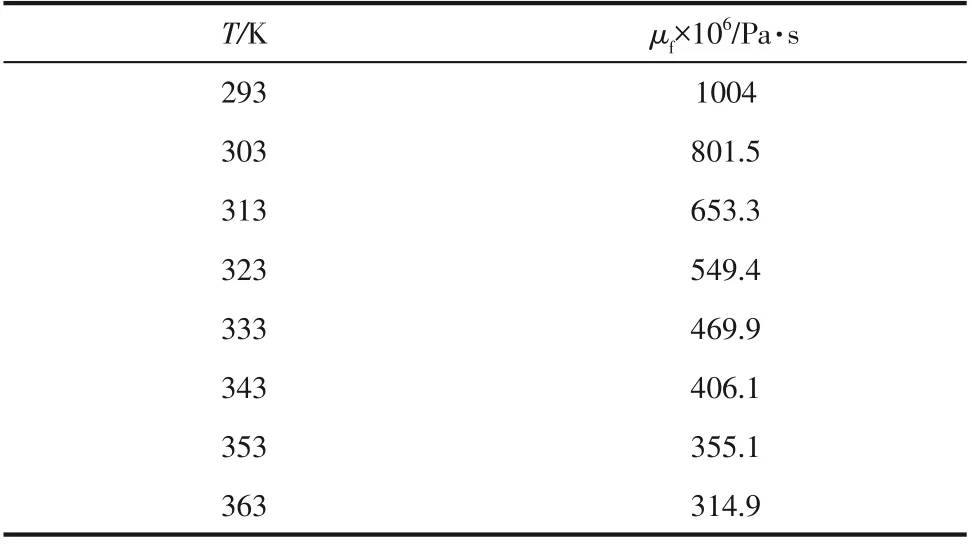
表2 不同温度下,去离子水的动力黏度值
三维无内热源的微通道内强迫对流传热的控制方程如式(1)~式(4)。
连续性方程

动量方程
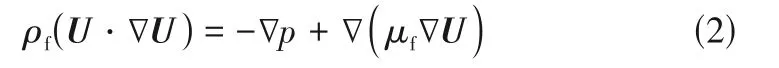
能量方程
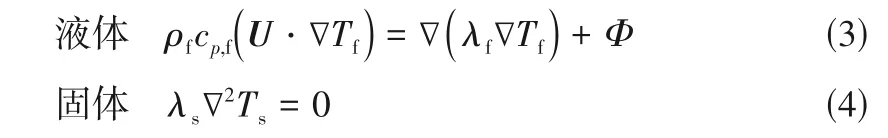
式中,、、c、、、、分别为速度矢量、密度、比热容、热导率、动力黏度、温度、耗散函数。下角标f表示流体,s表示固体。
模拟计算的边界条件见表3。

表3 数值模拟的边界条件
3 结果与讨论
3.1 模型验证
网格独立性检验,以RL=0.5 为例,分别对网格数25 万、73 万和108 万情况下,微通道内流动和传热过程进行数值模拟。结果表明,=440时,网格数25 万的微通道压降及平均努塞尔数()与网格数108 万相比,相对误差分别为2.174%和3.845%。网格数73 万时,与网格数108 万相比,相对误差分别为0.834%和0.692%,可见网格数73万时计算结果足够精确。因此,选取网格数73 万进行计算。
进而检验模型的准确性,考虑入口效应,矩形微通道的压降计算如式(5)。
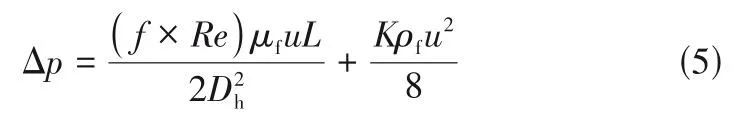
式中,、分别为水力直径和入口流速。参数由通道的宽高比AR决定,如式(6)。

图2 为热沉压降随的变化曲线。可以看出,所有热沉的压降均随升高而增大。图中将矩形光滑微通道(SM)的模拟值与理论计算值进行了比较,两者一致性较好,最大相对误差为9.96%。此外,带有周期性扰流结构的微通道的压降明显高于微通道SM,且凹穴几何结构对压降的影响随着增大越发明显。当一定时,压降随梯形凹穴底边缩短呈现先增大后下降,其中RL=0.7 的微通道压降最高,而RL=0的热沉压降最低。

图2 微通道热沉的压降随Re的变化
为了进一步验证该模拟方法对于带有周期性扰流结构的复杂热沉的有效性,计算RL=0.5 时,复杂热沉进出口流体温差的理论值,计算如式(7)。

式中,和分别表示热沉加热面积和通道入口面积。
图3比较了带有周期性扰流结构的微通道(RL=0.5)内流体进出口温差的模拟值和理论值。由图3可知,模拟结果和理论计算结果随的变化趋势一致,两者非常吻合,最大误差为3.73%,说明该模拟方法对于本文的复杂热沉具有良好的准确性。
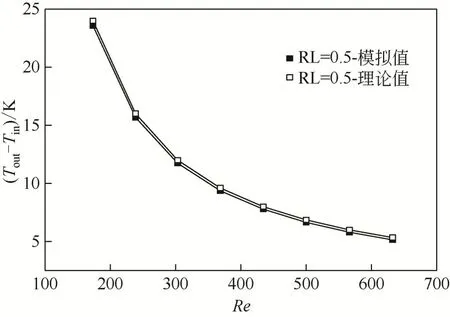
图3 带有周期性扰流结构的微通道(RL=0.5)内流体进出口温差的模拟值与理论值
3.2 流动和传热特性
图4 为=440 时微通道-平面内的流线分布。可以看出,光滑微通道SM 内流线相互平行,凹穴和针肋组成的周期性扰流结构使复杂通道的流场与通道SM 明显不同。由于凹穴的喷射-节流作用和针肋的分流作用,在凹穴内部和针肋下游均出现了旋涡。随着RL 减小,凹穴面积减小,凹穴内部的旋涡也明显缩小。这是因为随着RL 减小,流体对凹穴收缩段的冲击增强。此外,随着RL减小,针肋下游旋涡略有增大,RL 对针肋下游旋涡的影响较小。
图5给出了不同热沉内/随的变化。选取微通道SM 作为对比通道,下角标0 代表微通道SM 的模拟结果。由图5 可知,由于周期性扰流结构在通道局部引发了二次流,加之针肋对主流的阻挡,复杂微通道的摩擦系数高于微通道SM。随着增大,RL对摩擦系数的影响越来越明显。当RL减小时,凹穴内的旋涡减小,局部压降减小,降低;但RL 减小时,凹穴形状变化,流体对凹穴收缩段的冲击增强,这使升高。上述两种作用共同影响摩擦系数。较小时,RL 变化对旋涡影响较小,流体对凹穴的冲刷作用影响较大。因此,=173 时,RL=0 的热沉摩擦系数最大。较大时,旋涡变化对摩擦系数的影响占据主导,RL 较小的热沉内凹穴处的旋涡较小,因此摩擦系数较低。当=635时,RL=0的热沉比RL=0.7的热沉摩擦系数减小了10.2%。
=440时,热沉内的温度场如图6所示。在微通道SM内,流体温度由中心向侧壁逐渐升高,温度分布很不均匀。而复杂热沉内,通道侧壁附近流体的温度以及通道间肋壁的温度均显著降低,均温性更好。这是由于周期性微结构使流体对通道侧壁的冲刷增强,通道中心的冷流体和通道侧壁处的热流体能够高效混合。当RL=0.9 时,凹穴扩张段附近的流体温度较高。由图4可知,这是因为RL=0.9时凹穴内旋涡最大且靠近侧壁,形成层流滞止区,无法及时将热量带走。RL 由0.9 减小到0.5 时,由于微通道传热面积减小,通道间肋壁温度略微升高。随后,RL 减小使流体冲刷作用增强,通道肋壁温度降低。
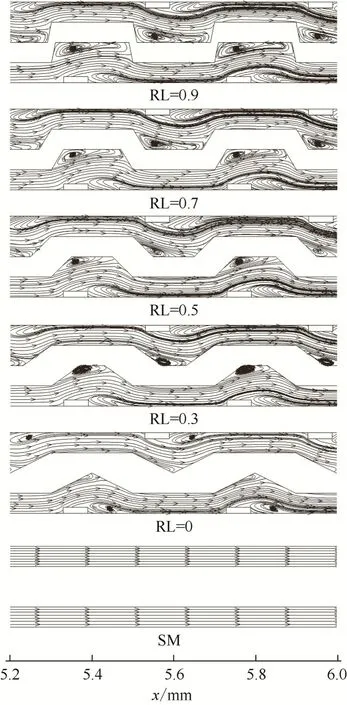
图4 微通道内流线分布随RL的变化

图5 不同RL条件下,fapp/fapp,0随Re的变化
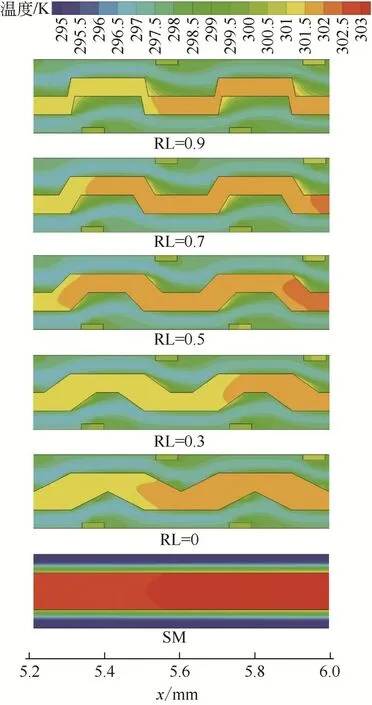
图6 微通道内温度场随RL的变化
微通道热沉底面与微型器件直接接触,其温度特性直接关系到微型器件的工作性能和使用寿命。图7 给出了不同下热沉的底面平均温度。随着升高,所有热沉温度均降低,但降低的速率逐渐减小。与微通道SM相比,新型热沉的温度显著降低。较低时,传热面积对散热效果影响较大,因此随着RL减小,凹穴面积减小,热沉温度升高。高下,由图4、图6可知,RL越小,凹穴处的层流滞止区越小,因此热沉温度越低。当=635时,与热沉SM相比,RL=0的热沉温度降低了8.33℃。

图7 不同微通道热沉的底面平均温度随Re的变化
图8 为不同热沉/随的变化。/均大于1,再次证明了扰流微结构的强化传热作用。随着增大,/迅速增大,但高于440后,曲线趋于平缓,说明微结构强化传热效果趋于稳定。<440 时,RL=0.3 的热沉传热效果最 好;≥440 时,RL=0 的 热 沉/最 高。RL=0 时凹穴由等腰梯形变为等腰三角形,三角形凹穴的扩缩变化更剧烈,因此散热效果提升。当=635 时,RL=0 的热沉的是通道SM 的2.26倍,比RL=0.9的热沉高16.5%。

图8 不同微通道热沉内,Nuave/Nuave,0随Re的变化
3.3 熵产特性
由热力学第二定律可知,通道内流动及传热过程存在不可逆损失。比较不同热沉的流动熵产和传热熵产,能够分析热沉的热力性能和传热效率。Bejan建立了通道内部流动与传热的熵产模型,提出流动熵产率、传热熵产率及总熵产率,如式(8)~式(10)。

熵产增大数表示改进热沉的总熵产率与参考热沉总熵产率的比值,即式(11)。

式中,̇代表通道SM的总熵产率。
图9(a)和(b)分别比较了̇/̇和̇/̇随的变化。如图9(a)所示,̇/̇>1 说明扰流结构增大了流动不可逆损失,且流速越高,流动熵产增大得越多。低下,RL减小使流动面积减小,导致流动阻力增大,流动不可逆损失增加。RL=0 的热沉流动熵产略高于其他热沉。高下,RL 减小导致凹穴内旋涡减小(图4),局部压降减小,从而流动不可逆损失降低。当=635 时,与RL=0.7 的热沉相比,RL=0 的热沉流动熵产降低了10.3%。

图9 不同微通道热沉内Ṡgen,∆p/Ṡgen,∆p,0和Ṡgen,∆T/Ṡgen,∆T,0随Re的变化
由图9(b)可知,̇/̇明显小于1,周期性扰流结构有效减小了传热不可逆性。<440时,随着增大,传热熵产大幅降低。周期性扰流结构引发的混沌混合降低了流体的温度梯度,减小了传热不可逆性,提高了换热效率。但>440时,曲线趋于平缓,甚至有增大趋势。这意味着,与微通道SM相比,虽然新型热沉仍然能够减小传热不可逆性,但高下,微结构增强传热的作用有所削弱。当≤440 时,RL=0.3 的热沉传热熵产率最小;>440时,RL=0的热沉传热不可逆损失最低。
图10 比较了不同热沉的熵产增大数。均小于1,说明凹穴和针肋对于减小不可逆损失,提高传热效率具有显著作用。随着增大,所有热沉的先减小后增大。主要原因是:低下,传热熵产率在总熵产率中占据主导,导致随增大而减小;高下,扰流结构使流动摩擦损失升高,造成增大。此外,当≤440时,随着RL增大,先降后升,RL=0.3的热沉最低,热力性能最佳;而当>440 时,随着RL 增大,逐渐降低,RL=0 的热沉不可逆损失最低。低时,RL=0 的热沉较大是因为:通道的传热面积较小,传热不可逆性较大[图9(b)],加之凹穴变为三角形,流动面积缩小,流动阻力增加,导致流动不可逆损失较大[图9(a)],因此较大。而高时,RL减小使凹穴内的旋涡显著减小,摩擦损失降低,流动不可逆性大幅减小,使得RL=0 的热沉总熵产较小。
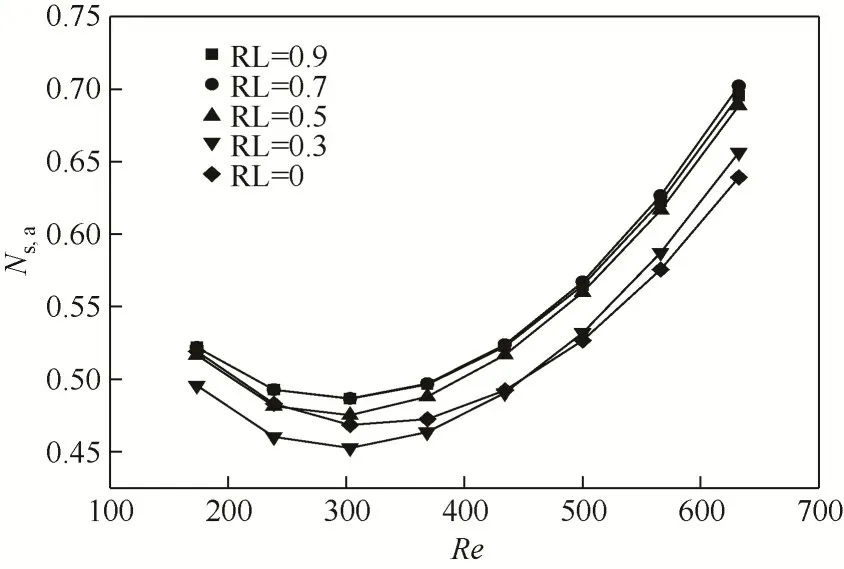
图10 RL对熵产增大数的影响
3.4 综合性能
由上述结果可知,与微通道SM 相比,周期性扰流结构能够显著增强传热,但同时会造成压降和流动摩擦损失增大。因此,利用总热阻随泵功的变化评价热沉的综合性能。总热阻和泵功分别用式(12)、式(13)表示。
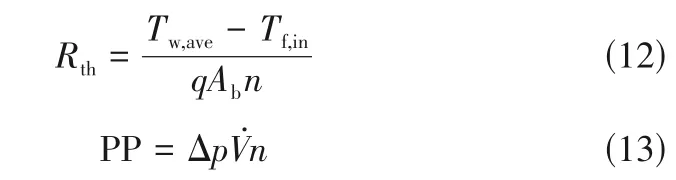

由图11可知,与微通道SM相比,当泵功一定时,改进后热沉的总热阻显著降低;当热阻一定时,新型热沉的泵功明显减小,周期性扰流结构显著提高了热沉的综合性能。可以看出,较低泵功下,RL=0.3 时热沉的总热阻最小;较高泵功下,RL=0 的热沉总热阻最小。PP=0.070W 时,微通道SM 的热阻为0.804K/W。而当PP=0.087W 时,RL=0.3 的热沉热阻为0.491K/W。上述两种工况的泵功相近,但与热沉SM相比,RL=0.3的热沉热阻降低了38.9%。

图11 微通道热沉的热阻随泵功的变化
采用强化传热因子衡量传热的增强和压降的增加,评价热沉的综合性能,如式(14)所示。

随泵功的变化如图12所示。由图12可见,均大于1,说明传热增加量大于压降增加量。带有周期性扰流结构的热沉比传统热沉综合性能更优。随着泵功增大,先上升后下降。由图5、图8 可知,随着流速增大,复杂热沉的/增大的速率减慢,而/迅速升高,两者的综合作用使在高泵功时呈现下降趋势。可以发现,综合考虑传热和压降,当PP≤0.054W 时,RL=0.3 的复杂热沉综合性能最佳;当PP>0.054W 时,RL=0 的热沉综合性能最佳。RL=0.3和RL=0的热沉能够及时带走通道侧壁处的热量,凹穴处的旋涡较小,流动摩擦损失较小,因此能够在显著增强传热的同时保持压降较低。

图12 微通道热沉的强化传热因子随泵功的变化
4 结论
本文数值研究了带有周期性扰流结构的微通道热沉内流体流动和传热过程,利用熵产原理分析了该热沉内流动和传热不可逆损失随微结构几何参数的变化规律,指出影响微通道传热效率的本质因素,利用热阻和强化传热因子评价了热沉的综合性能,得出如下主要结论。
(1)周期性扰流微结构能够使通道局部出现旋涡区,产生混沌对流。减小RL 使凹穴面积减小,导致流体对凹穴收缩段的冲刷增强,凹穴内部的旋涡明显缩小。高时,通道压降和摩擦系数随RL减小呈现明显降低。RL 减小有利于减小凹穴内的层流滞止区,降低热沉温度,增强传热。
(2)低下,RL 减小使流动不可逆损失增加;高下,RL减小使流动摩擦损失减小,从而流动不可逆性减小。周期性扰流结构引发的混沌混合能够降低流体的温度梯度,减小传热不可逆损失,提高热沉的换热效率。从熵产角度看,当≤440 时,RL=0.3 的热沉热力性能最佳;当>440时,RL=0的热沉不可逆损失最小。
(3)由于在显著强化传热的同时流动阻力相对较小,当PP≤0.054W 时,RL=0.3 的复杂热沉综合性能最佳;当PP>0.054W 时,RL=0 的热沉综合性能优于其他热沉。与传统微通道SM相比,在相近的泵功下,RL=0.3 的微通道热沉热阻降低了38.9%。当PP=0.086W 时,RL=0 的复杂热沉的强化传热因子为1.51。

