基于多策略集成优化算法的己烷油精馏过程3E多目标优化
代敏,杨福胜,张早校,刘桂莲,冯霄
(西安交通大学化学工程与技术学院,陕西 西安 710049)
己烷油作为溶剂油的一类,已被广泛用于金属冶炼、化学工业、食品工业、医药工业等行业,生产高附加值和环保型溶剂油产品成为发展的方向。工业己烷油产品的质量与收率除受原料性质和反应工序影响外,更与精馏工序的操作条件息息相关。无论原料来源如何,精馏工序能耗均达到己烷油生产总能耗的70%以上,而高能耗通常又伴随着显著的温室气体排放。可见,产品高收率、装置低能耗与温室气体低排放具有矛盾对立的复杂关系。因此需要一个严格的优化策略来帮助考虑多个目标(能源、经济和环境)的决策,使其在节能减排的同时保持过程经济性。
目前有关溶剂油精馏过程的改造和优化的研究多有报道。例如,苏洋用Aspen Plus 对己烷油精馏过程进行了模拟,分别讨论了塔板数目、回流比、馏出量等因素对能耗和产品收率的影响,并提出了上述影响因素的最优组合。肖兴等从水力学核算角度出发设计并建立了溶剂油分离过程的数学模型,可在保证产品质量的同时满足收率要求。Lorimer 等利用一维线性平流扩散方程的数值解,对混合热溶剂油回收过程中的传质机制进行了灵敏度分析。然而,大多研究都是对溶剂油精馏过程的能耗和产品质量等指标进行单目标优化,其结果往往具有片面性,未能将上述能源、环境和经济方面的各指标作为一个整体进行全局的操作参数优化。
近年来,一种模拟生物界中自然进化的多目标进化算法,因其对待解问题的数学性质不敏感,在石油化工过程的多目标优化中受到越来越多的关注。由于一次能求多个等价解且所需参数较少,基于Pareto占优的非支配排序遗传算法(NSGA-Ⅱ)是应用较广的算法之一。然而,由于其进化过程的随机性,难以摆脱收敛速度慢和解分布特性较差的问题,特别是对于具有复杂Pareto 前沿和高维多目标优化问题。因此,需要探索新的种群进化机制,即如何进行有效的基因操作促进种群进化,使其较快收敛并兼顾全局搜索能力和局部开发能力。
Zhao 等通过引入精英解信息指导交叉操作,提出了基于自适应多种群多交叉的改进NSGA-Ⅱ算法以提高算法的收敛能力,但操作过程略显复杂。Chen等借鉴差分进化的思想提出了基于双向邻域搜索的策略以提高算法的收敛速度和分布性,但增加了种群非支配排序过程的计算量。Kurniawan 等为了提高算法的收敛速度和局部搜索能力,在个体进化过程中加入了局部搜索以指导个体的选择和扰动的确定,但随着进化代数的增加,产生的大量局部解将增加计算负担。可见,多种变体进化机制在一定程度上可以促进原始NSGA-Ⅱ的性能提升,不足之处在于增加了额外的计算负担且实施复杂。这促使研究者提供新的改进策略,使其操作简单并且可在不改变时间计算复杂度的情况下提高NSGA-Ⅱ的收敛性和分布性。
综上,本文提出了基于多策略集成的改进NSGA-Ⅱ算法(MENSGA-Ⅱ),通过邻域引导策略和随机极限游走策略提高解的质量、降低计算时间。同时以己烷油精馏工艺为对象,基于实际生产数据建立了精馏工序的流程模型,并以能量、经济、环境影响为目标建立了3E 优化模型,并将MENSGA-Ⅱ用于3E 多目标优化求解以探究3 个目标之间的权衡,从而为己烷油精馏过程的操作优化提供决策依据。
1 MENSGA-Ⅱ
由于多策略搜索在求解高维复杂优化问题上的有效性,本文将多策略搜索与NSGA-Ⅱ算法相结合,并在算法中构造多策略搜索方程的协调使用机制。
1.1 邻域引导策略
精英解(全局最优)个体被广泛用于各种搜索方程以指导个体快速进化,特别是邻域搜索方程,但是对精英解的过度依赖往往也使得算法容易陷入局部最优。因此还需要利用其他欠优个体信息,使得算法在保证收敛性的同时兼顾种群分布性。事实上,在多目标优化问题中,对于种群个体而言,既有全局邻域最优个体又有局部邻域最优个体。因此在本策略中利用基于全局最优个体的邻域搜索来增强算法的局部寻优能力,利用基于局部最优个体的邻域搜索来确保种群多样性的同时进一步增强算法收敛性,如式(1)所示。
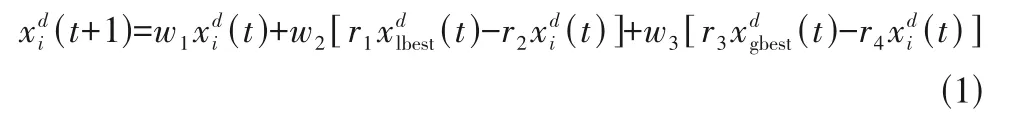
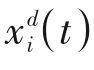
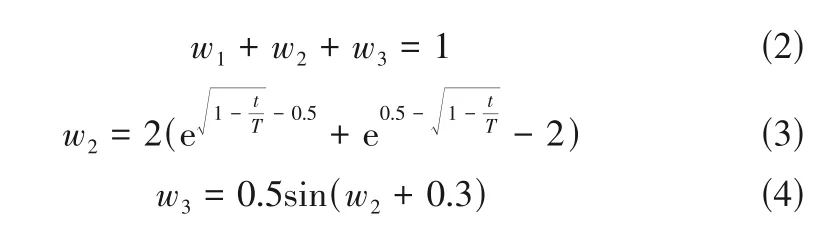
式中,为种群最大进化代数。
图1为、随进化代数的变化曲线,可以看出,、随着进化代数的增加呈现先缓慢降低后快速增加的趋势。这意味着在算法在迭代初期,种群可以在精英解周围进行快速、彻底的搜索,进而加速收敛,随着迭代的进行,种群对精英解的依赖开始逐渐减少,并开始关注精英解以外的未探索区域,进而增强解集的分布性。若对未探索范围的搜索无限放大,则会限制算法的收敛解集质量,因此在迭代后期,、急剧增加,使得种群在扩大搜索范围的同时也保证了收敛精度。如图2所示,以二维空间为例,当、较大时,更新后的个体更靠近全局最优个体和局部最优个体[图2(a)],进而保证了MENSGA-Ⅱ能快速逼近Pareto解集,当、较小时,更新后的个体更关注未探索区域[图2(b)],进而解集确保了解集分布性。
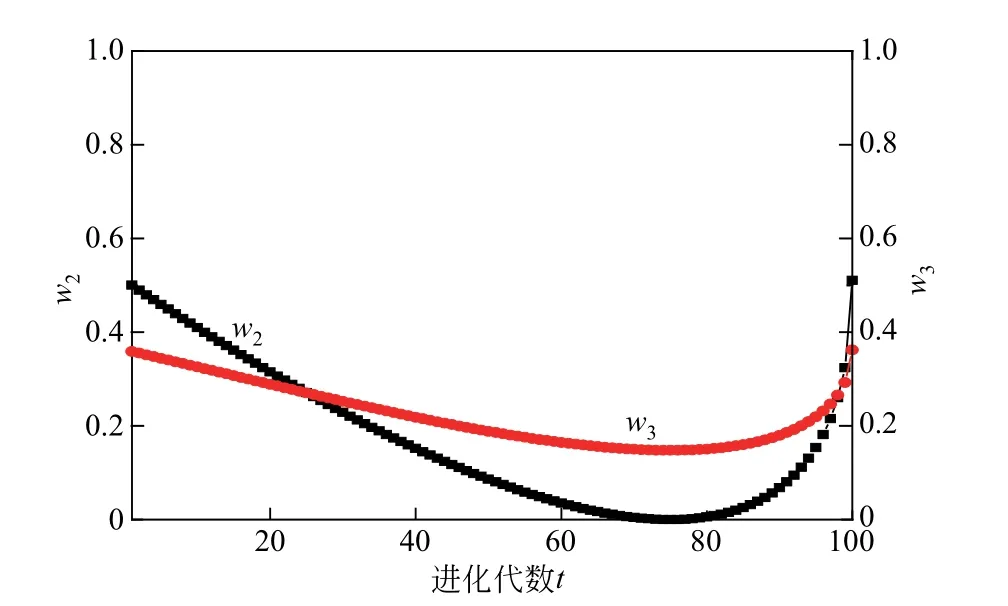
图1 w2、w3随进化代数的变化曲线
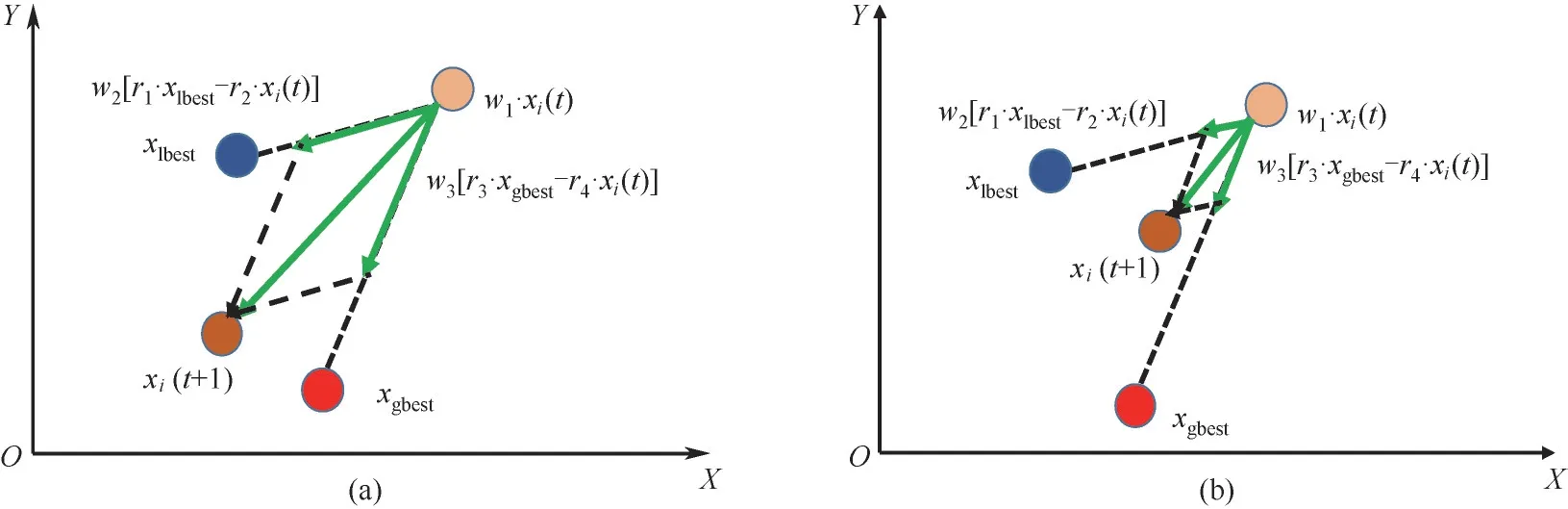
图2 基于邻域最优引导策略在二维空间的示意图
1.2 随机极限游走策略
随机游走策略,即每个个体按一定的步长游走来进行更新,被证明可以增加种群的全局搜索能力,进而改善解集的分布性。本文借鉴极限优化策略的思想,定义种群中个体的更新方式如式(5)~式(7)所示。
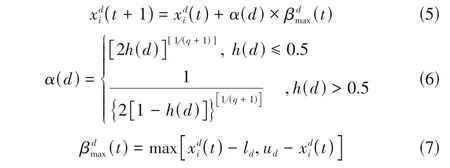
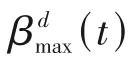
1.3 MENSGA-Ⅱ算法流程
综上,所提出的MENSGA-Ⅱ算法的主要框架如图3所示。首先对种群进行随机初始化。然后按照NSGA-Ⅱ的标准计算个体的适应度值和拥挤距离,并对个体进行非支配排序。接着对种群进行进化操作形成子代,在这个过程中,通过设置概率参数来实现对不同搜索策略的切换,使每个个体的更新机会均为1次,从而不增加计算复杂度。由于邻域引导策略带有全局最优解和局部最优解的信息,且两者权重可以自适应调整,因而可以加快收敛速度并改善解的多样性,故其被采用的概率较大,设为0.5;而在进化后期,种群个体较为集中,此时随机极限游走策略的全局搜索性变弱,因此设置其被采用的概率随着进化代数的增加逐渐变低,如式(8)所示,其中,为种群最大进化代数。此外,对于有约束多目标优化问题,本算法采用罚函数法将目标函数转为无约束问题,如式(9)、式(10)所示。其中,为解集中最差解的函数值;() 为惩罚函数,表示个体违反约束条件的程度或与可行域之间的距离。最后合并父代和子代,对其进行非支配排序和拥挤距离计算以选取下一次参与进化的父代。重复上述操作直到达到最大迭代次数,此时得到的非支配解即为最终的Pareto最优解。
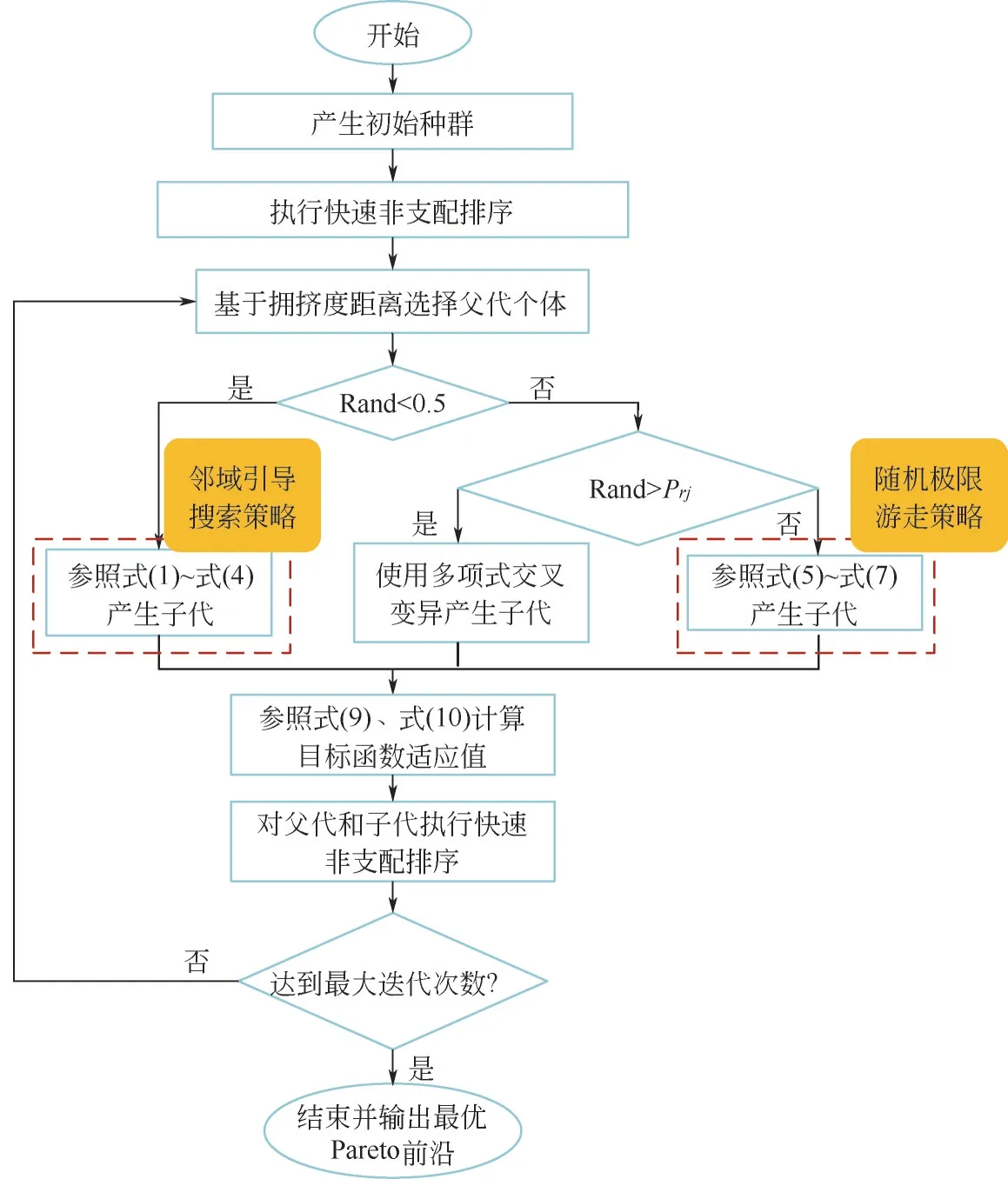
图3 MENSGA-Ⅱ算法的流程图
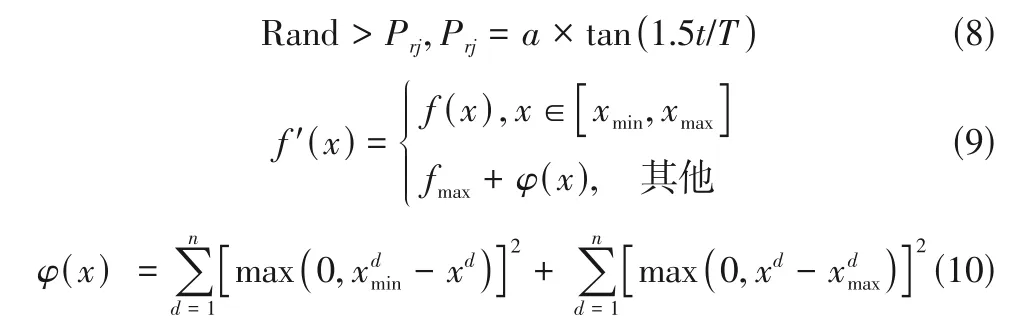
1.4 计算复杂度分析
MENSGA-Ⅱ算法主要包括种群的初始化、快速非支配排序、多策略进化、拥挤度选择操作。在每一次迭代计算过程中,相应操作最坏情况下的计算复杂度分别为(∙)、(∙N)、(∙∙)和(∙lg),其中为种群数目,为决策变量数目。因此,MENSGA-Ⅱ的计算复杂度可表示为(∙N),与NSGA-Ⅱ相同。可见尽管MENSGA-Ⅱ增加了多策略搜索,但并未显著增加计算复杂度和负荷。
2 标准函数测试
2.1 实验设置
本文实验是在Windows 10 系统下运行多目标优化PlatEMO平台实现的。为了检验MENSGA-Ⅱ的性能,本文选取了4个两目标函数和4个三目标函数进行了测试,其简要描述见表1。并将MENSGA-Ⅱ算法的优化性能与经典的NSGA-Ⅱ算法、基于分解的多目标进化算法(MOEA/D)以及Epsilon-多目标进化算法(e-MOEA)进行了比较。上述测试函数和对比算法的代码均来自PlatEMO平台,各算法的主要参数设置如表2所示。为了消除种群初始化和优化路径的随机性对算法性能的影响,对每种算法进行了30次独立优化实验。对于两目标问题,种群大小为100,评估次数为10000;对于三目标问题,种群大小为200,评估次数为20000。选取PlatEMO 平台中的综合性能评价指标(IGD)来评估不同算法的性能,IGD 的值越小,说明解集收敛越好,分布越均匀。
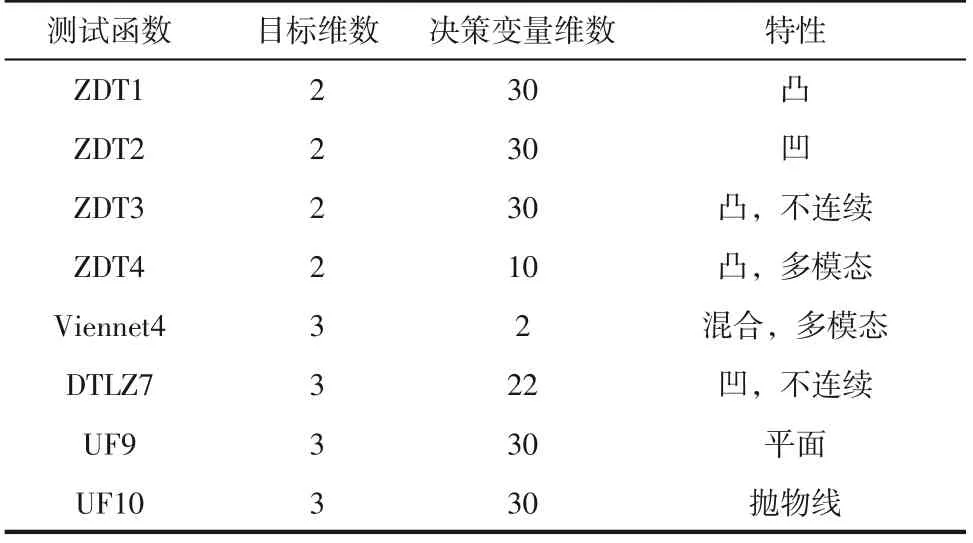
表1 标准测试函数及其特性

表2 各对比算法的主要参数设置
2.2 结果与分析
4种算法独立进行30次实验得到的IGD箱线图如图4 所示。显然,MENSGA-Ⅱ在上述问题的优化性能上占据绝对优势,其均具有最小的均值。进一步采用显著性水平为5%的Friedman 检验给出了4 种对比算法的平均排名,如表3 所示。其中MENSGA-Ⅱ稳定排名第一,优化性能突出。一方面,这证明了所提方法在改善Pareto边界收敛性和分布均匀性方面的有效性,另一方面也可表明MENSGA-Ⅱ可以较好地处理高维复杂前沿的问题。这种优势可以归因于MENSGA-Ⅱ在种群进化过程中融入了精英个体的信息以引导个体更新,进而促进算法收敛,并加入了全局随机搜索,进而增强了对潜力区域的局部开采和全局勘探。此外,进化相比于其他3 种算法的分布情况,MENSGA-Ⅱ算法在大部分测试问题上的分布更为集中,这也说明了本文所提算法的鲁棒性更好。
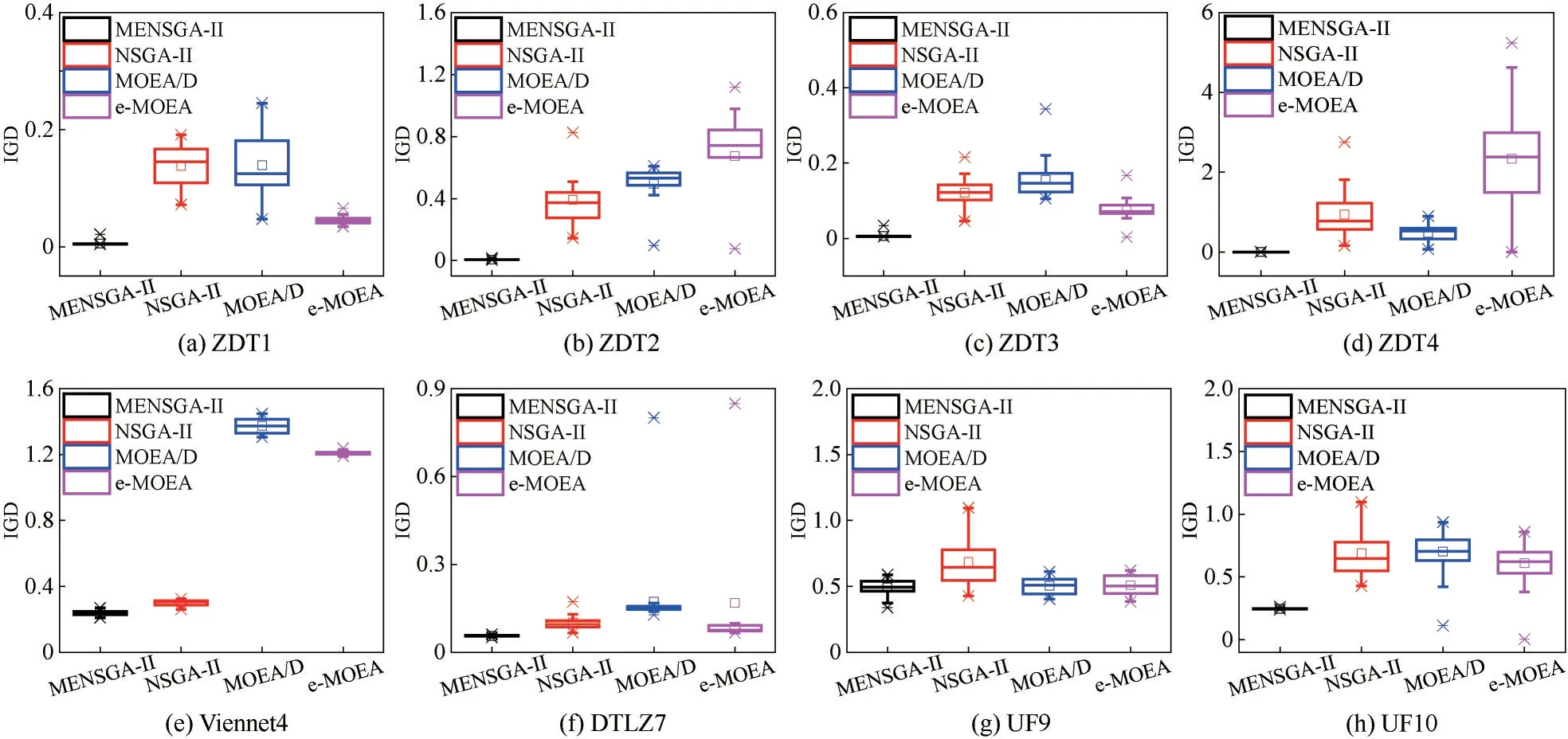
图4 4种算法独立运行30次IGD结果的箱线图

表3 基于IGD的各对比算法的平均排名
为了更直观地显示各算法的收敛性和解集的多样性,绘制了一些较难测试问题(ZDT3、ZDT4、DTLZ7 和UF10)第一次运行实验得到的Pareto 前沿,如图5所示。可以看出,无论是对于两目标问题中的不连续ZDT3 函数和多模态ZDT4 函数,还是对于三目标问题中DTLZ7 和UF10 等复杂抛物线前沿问题,MENSGA-Ⅱ算法获得的解集均可以充分逼近真实Pareto前沿,并具有较好分布性,而其他比较算法甚至无法收敛到真实Pareto 前沿附近。上述结果进一步证明了MENSGA-Ⅱ算法能够解决高维复杂问题。
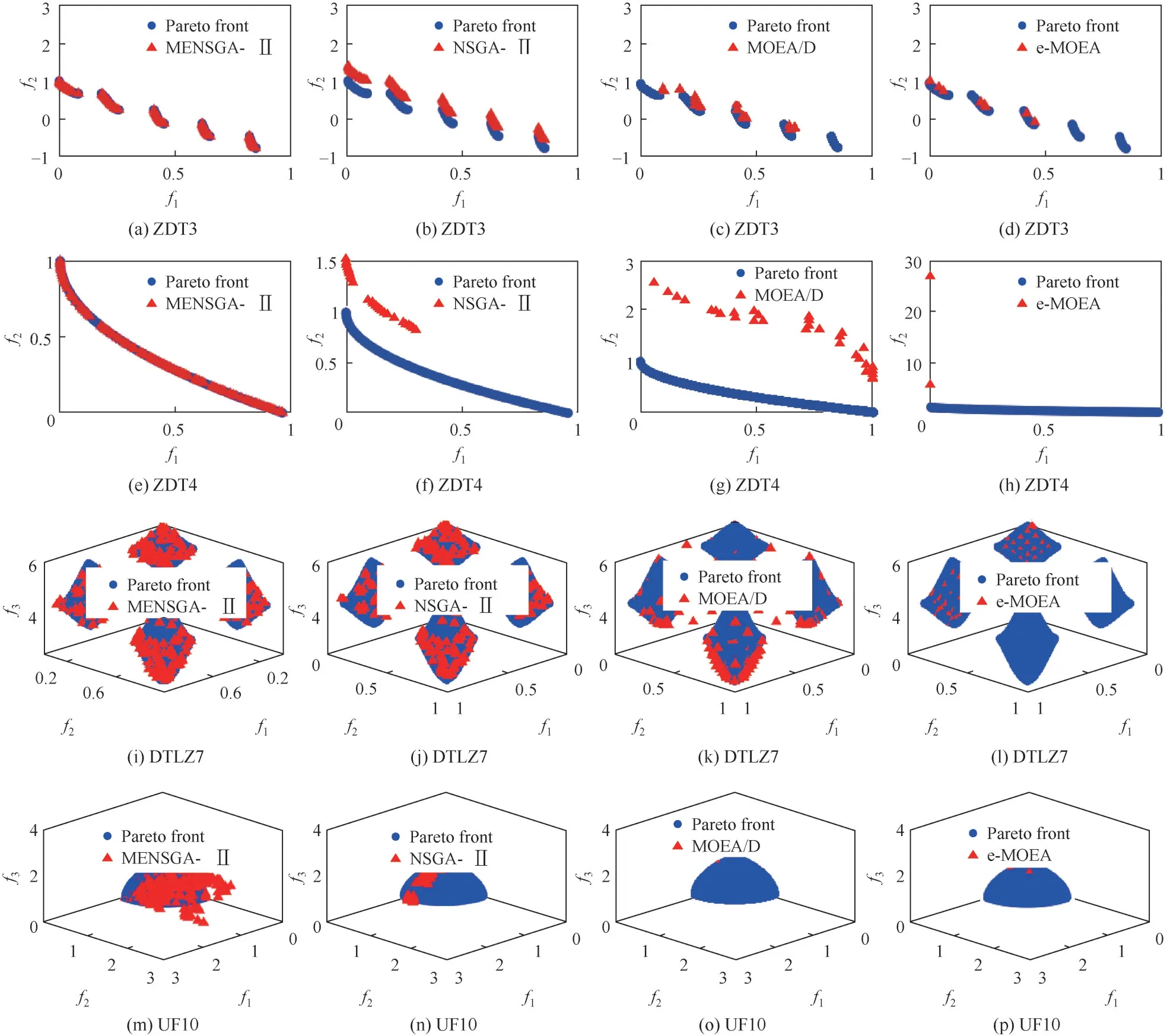
图5 4种算法在ZDT3、ZDT4、DTLZ7和UF10测试函数上的Pareto前沿
进一步绘制上述算法的IGD 指标收敛曲线图(见图6)。可以看出,对于几乎所有测试问题,MENSGA-Ⅱ均具有稳定和最佳的收敛速度,即IGD 指标下降均为最快,并都得到了最小化IGD值。这表明在大多数情况下,MENSGA-Ⅱ可以有效地加速收敛并提高Pareto 解的收敛精度和分布性。由此可推测多种进化策略的协同组合可以使算法跳出局部最优,提高优化性能。综上,MENSGA-Ⅱ算法的有效性得到了证明。

图6 4种算法在测试函数上的IGD指标收敛速度曲线
3 己烷油精馏过程多目标优化
3.1 己烷油精馏过程模型搭建
本文以文献[3]建立的精馏模型为依据,应用流程模拟软件Aspen Plus建立的己烷油精馏过程如图7所示,其中状态方程选用Peng-Robinson 方程。该装置采用了一个顺序分离过程,来自精制工段的饱和粗己烷首先通过脱轻组分塔分离C及以下轻组分,塔釜饱和液体则进入异己烷塔精馏分离,在塔顶得到95%(质量分数)异己烷产品,塔釜饱和液体则送入正己烷塔分离正己烷和更高沸点的庚烷,最终在塔顶得到90%(质量分数)正己烷产品,塔釜采出庚烷组分。
3.2 己烷油精馏过程模型验证
主要设备质量流量的实际运行数据与仿真结果的对比如表4所示。可以看出,模拟结果与实际工况数据吻合较好,平均绝对误差小于0.2%,表明所建立的仿真模型可用于工艺分析和优化。
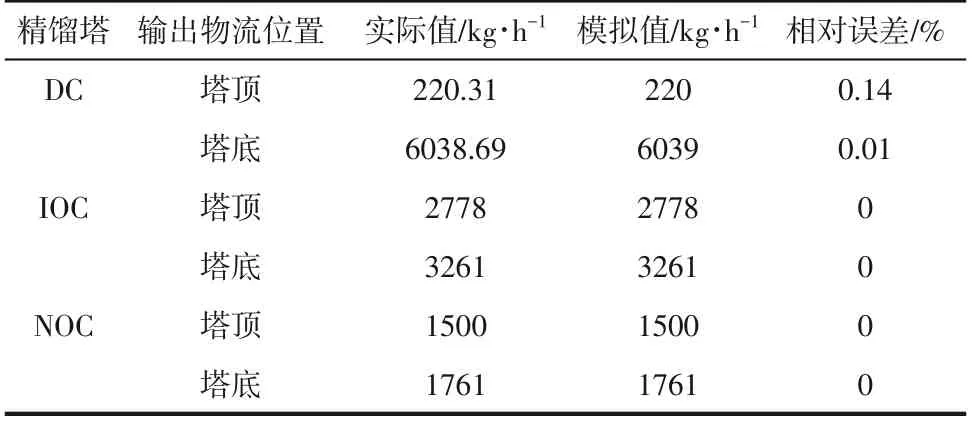
表4 仿真结果与实际数据的比较
3.3 面向3E的多目标优化模型构建
3.3.1 能源消耗分析
在本文中,能耗设备主要包括图7中的精馏塔冷凝器和再沸器。因此,以年度总公用工程(ATU,kW/a)作为能耗目标,其由总热公用工程(THU,kW/a)和总冷公用工程(TCU,kW/a)组成,如式(11)所示。
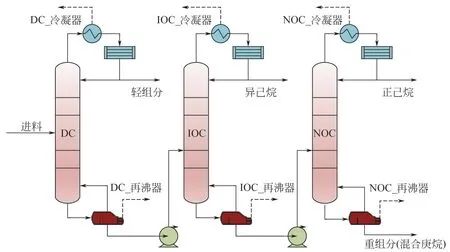
图7 己烷油精馏装置流程图
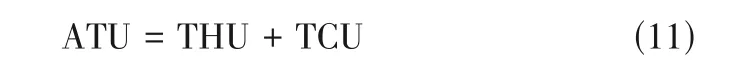
3.3.2 经济分析
利润最大化是企业普遍追求的经济目标。在本案例中,定义经济潜力为年度毛利润(AGP,USD/a),即产品的年度总收入(PR,USD/a)与年度总成本(TAC,USD/a)之间的差额,如式(12)~式(14)所示。

式中,PP 表示产品价格,异己烷油和己烷油的价格分别为1.25USD/kg 和1.2USD/kg;MF 为产品质量流量;为年运行时间,设定为8000h;Capc 为生产成本,USD;Opec 为运行成本,USD;PB为投资回报期,设定为3年。TAC由固定成本和能耗成本构成,其中固定成本包括塔设备成本(不包括塔内件,Colc)、冷凝器成本(Conc)、再沸器成本(Rebc)和泵成本(Pumc),各设备成本计算方式如式(15)~式(18)所示。

式中,、分别为塔径和塔高,m;和分别为冷凝器和再沸器热负荷,kW;Δ和Δ分别为冷凝器和再沸器传热温差,K;为泵能耗,kW;、、分别材料、设计压力和设计温度的关联因子,本项目分别取1、2.1 和1.5。总能耗成本即式(11)中总公用工程(TU)的消耗,即冷却水和中低压蒸汽, 采用Aspen Energy Analyser(AEA)对其进行评估。
3.3.3 环境分析
环境分析在评价过程系统的综合性能方面起着至关重要的作用,其可以被量化为碳排放。本案例的塔体设备均采用碳钢材料,碳钢的碳足迹(CF)假定为0.72kg CO/kg碳钢。此外己烷油精馏过程会消耗大量能量,使用AEA 对其二氧化碳排放当量进行评估,计算过程如式(19)所示,其中和为能源的效率因子和排放因子。因此,整个过程的年度碳排放(ACE,kg/a)如式(20)所示。
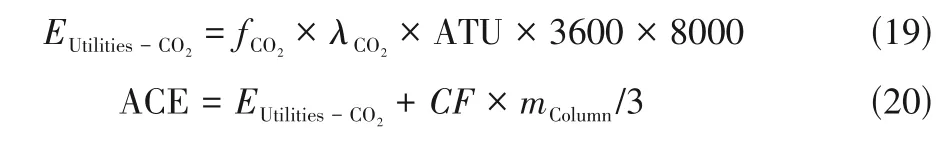
式中,表示年度公用工程碳排放,kg/a;为塔设备所用碳钢的质量。基于上述考虑,本案例的多目标优化模型表述如式(21)和式(22)所示。

式中,、分别表示异己烷油、己烷油的质量分数,%。为了符合设计要求,规定异己烷油和己烷油产品的纯度分别不小于95%和90%。该模型对应的决策变量及其边界如表5所示。
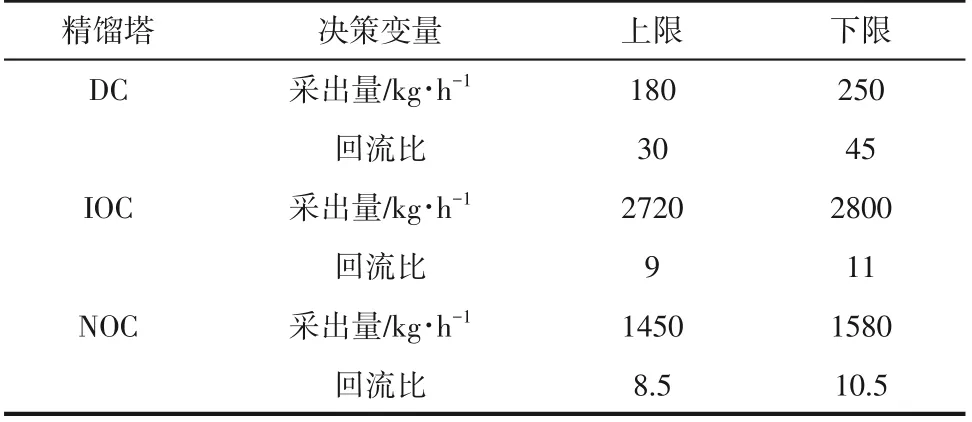
表5 己烷油精馏模型的决策变量及其边界
3.4 优化计算结果分析
为了进一步评价MENSGA-Ⅱ处理实际高维复杂问题的性能,采用MENSGA-Ⅱ和在标准测试函数中排名第二的NSGA-Ⅱ和排名第三的e-MOEA分别对己烷油精馏过程的3E 多目标模型进行优化求解。在每次迭代优化过程中,各优化算法不断调用Aspen Plus 模拟精馏过程,并根据模拟结果和当前解的信息对优化搜索过程进行评估和修改,直到满足终止条件。其中种群规模设为90,其余参数设置与2.1 节相同。算法的终止准则是,如果连续五代的Pareto前沿变化不大,则认为目标函数已经收敛。图8(a)~(c)为上述算法在第30代和第35代获得的Pareto前沿,可以看到其非常接近,各算法已达到收敛条件,因此最大进化代数设为35。图8(d)对比了各算法在第35 代的Pareto 前沿,相比于NSGA-Ⅱ和e-MOEA,MENSGA-Ⅱ算法获得的Pareto前沿具有相对均匀和更宽广的分布,弥补了传统优化方法的不足,从而可为决策者提供更充分的选择空间。这也表明MENSGA-Ⅱ对于实际工业高维复杂模型的优化具有一定潜力。
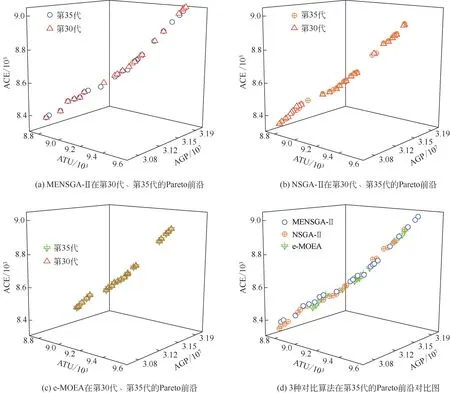
图8 各对比算法的Pareto前沿图
采用LINMAP 方法对MENSGA-Ⅱ得到的Pareto前沿进行决策分析(见图9),选取各指标最优工况下的操作点,各点对应的3E 性能指标和决策参数如表6所示。其中点既代表最小的年度总公用工程(8.78×10kW/a)又代表最小的年度碳排放(8.38×10kg/a),且该点对应年度毛利润最小(3.07×10USD/a);点表示最大的年度毛利润(3.19×10USD/a),该点对应的年度总公用工程和年度碳排放均最大,分别为9.46×10kW/a 和9.03×10kg/a。可见,能源消耗和CO排放之间存在正相关关系,由此可推测相比于塔设备制造带来的CO排放,过程能耗对精馏过程的CO排放量起着决定性作用。此外,年度毛利润随着能耗和CO排放量的增加而显著增加。究其原因,当产品收率较高时,馏出率和回流比的变化往往会导致大量的冷热效应,从而导致能耗相应增加,而CO排放量又与操作过程的能耗正相关。上述现象进一步印证了高收益产品总是伴随着较大的能耗和一定程度的环境影响。点为采用LINMAP 方法选择的Pareto 最优点,其距离理想点(所得Pareto 前沿最小ATU、ACE和最大AGP的交点)的距离最近。可以看到,当年度毛利润AGP 小于点(3.14×10USD/a)时,年度总公用工程ATU 和年度碳排放ACE 随AGP 的增加而缓慢增加,反之则随AGP 的增加而急剧增加。这可能是因为较高的能源消耗通常与更大的换热器面积相关,这会带来较大的年度总成本,因而经济收益增速减缓。与实际工况点相比,Pareto最优点的ATU、AGP 和ACE 可分别减少5.09×10kW/a、增加4.99×10USD/a 和降低4.82×10kg/a。可见,所选优化点无论从能耗、毛利润还是排放量,都要优于实际的工业操作条件,这表明可以通过操作参数的优化进一步改善精馏系统的操作。

图9 基于LINMAP的MENSAG-Ⅱ的Pareto前沿决策
进一步分析Pareto前沿对应的可调决策参数对3个目标函数的影响规律,如图10所示。由图10(a)可以看出,DC 的最优采出量主要集中在180~196kg/h,其主要分布在决策变量的下限,当其大于188kg/h 时,AGP 显著增大,ATU 和ACE 与之相反,处于较小值。由此可知,当DC 的采出量大于188kg/h时,精馏效果主要受轻组分脱除率的影响,采出量的略微增加可以带来显著的轻组分脱除效果,进而间接提高后续产品的收率,并且该过程几乎不增加对能耗的需求。与图10(a)相反,图10(c)反映了IOC的最优采出量主要集中在2790~2800kg/h,其分布在决策变量的上限,且随着采出量的增加,ATU、AGP 和ACE 在后半段呈现增加的趋势。可以分析得知,当采出量小于2795kg/h时,异己烷的回收率增速逐渐放缓,此时能耗的过多投入并不能带来异己烷产品的显著增加,而当采出量大于2795kg/h以后,采出量的增加可以较为明显地增加异己烷油产品收率,尽管会带来能耗的增加,但产品收益高于能耗增加所带来的操作费用。图10(e)为NOC 的最优采出量,可以发现当采出量小于1580kg/h时,ATU、AGP和ACE都会随着采出量的增大而呈现线性缓慢上升的趋势,值得注意的是,相比于ATU 和ACE,AGP 的增速更慢,当采出量固定为1580kg/h时,三者呈现直线上升趋势。这可能是因为采出量增加的同时带入了庚烷等重组分杂质,使得正己烷产品的收率呈现小幅增长,进而AGP 增速较缓,这表明在一定范围内,NOC 可以通过提高采出量进而达到最佳操作点消费。从图10(b)和(f)可以发现,DC 和NOC 的Pareto 点对应的回流比主要集中在[30,32]和[8.5,8.8],接近于决策变量的下限。由此可以推测当DC和NOC的回流比分别大于32和8.8时,过程能耗对精馏效果的影响更大,回流比的增加只会徒增总能耗,并不能换来显著的分离效果;而当回流比接近下限时,产量的略微降低可以显著降低总能耗,同时仍能保证所需的产品纯度。从图10(d)可以看到,ATU、AGP和ACE都随着IOC的回流比的增大而增大,当IOC的回流比大于9.6 时,三者的增速逐渐变慢。这可能是因为较大的回流比有利于异己烷组分的分离,尽管其增加了能耗,但异己烷的回收率和产品纯度的改善更为显著。上述分析也与表6中各决策变量的取值情况相互印证。
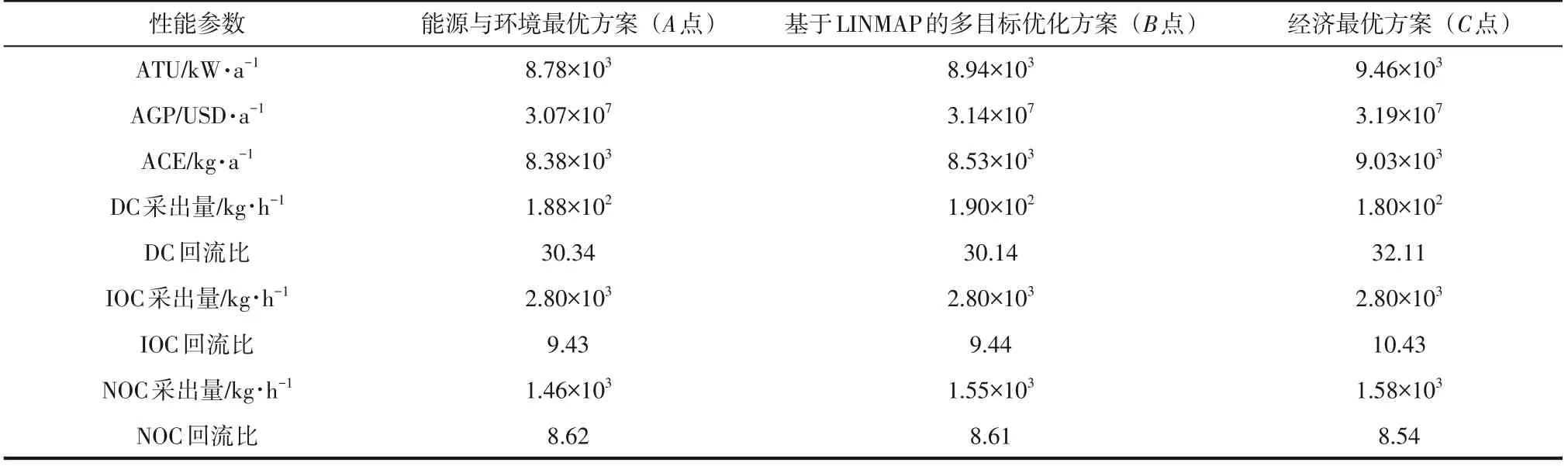
表6 不同代表工况下的3E目标性能指标及其对应的决策参数
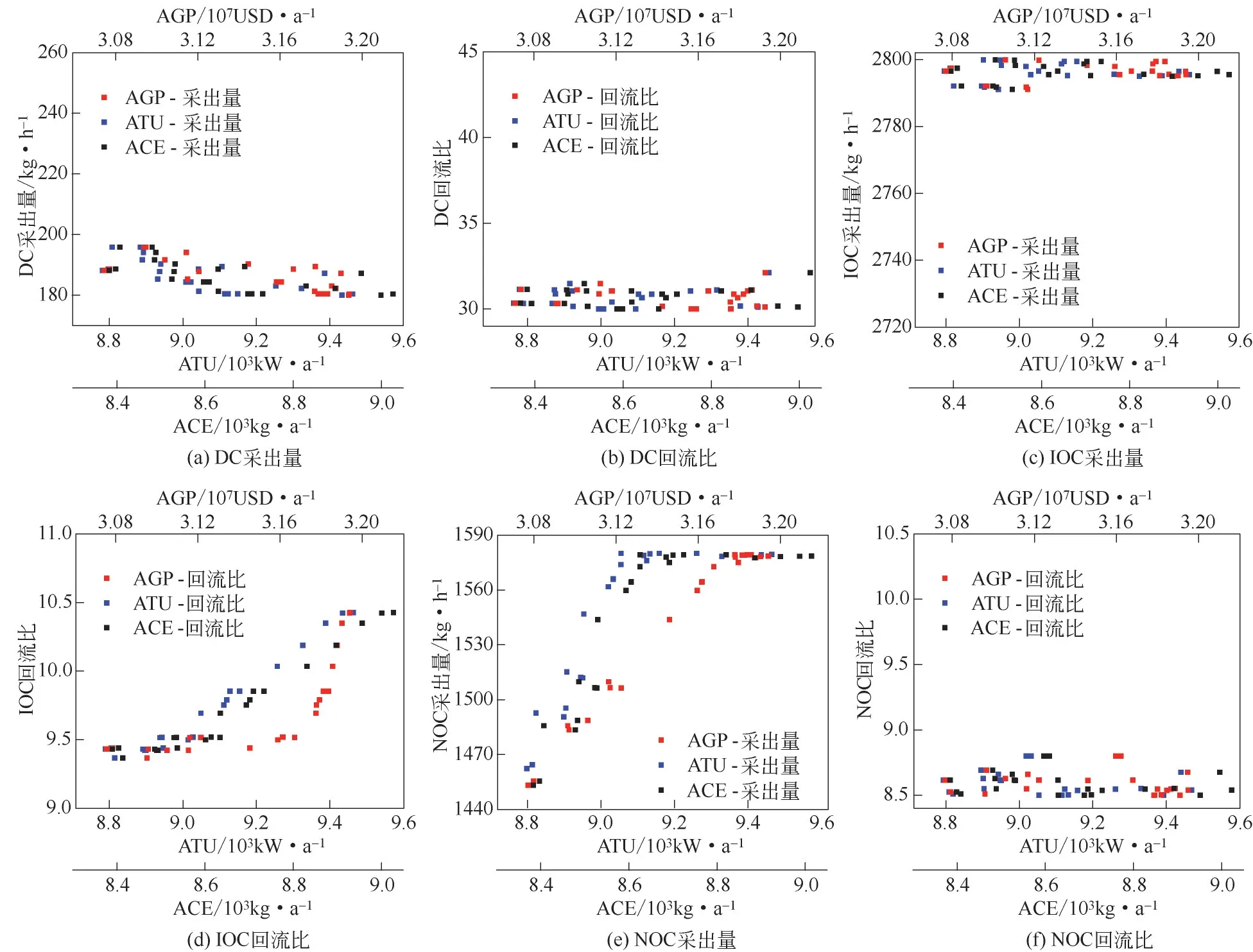
图10 MENSAG-Ⅱ得到的Pareto前沿对应的决策变量的分布情况
4 结论
本研究提出了一种基于多策略集成的多目标遗传算法(MENSGA-Ⅱ),并通过标准测试函数和己烷油精馏过程的3E 优化对其有效性进行了验证,得出以下结论。
(1)与经典的多目标优化方法(NSGA-Ⅱ、MOPSO、eMOEA)相比,不管是处理简单问题还是具有复杂Pareto 前沿的高维问题,MENSGA-Ⅱ在收敛性和解集均匀性方面均具备较为显著的优势,并且MENSGA-Ⅱ的鲁棒性更好。
(2)本文提出的基于邻域最优个体引导的进化策略可以加快个体更新,进而增强了算法的收敛速率和精度,也改善了解集分布;另一方面,提出的基于随机极限游走的进化策略则引导个体在全局内随机更新,便于实现对潜力区域的有效全局探索。
(3)与实际工况相比,典型优化工况下年毛利润可增加4.99×10USD/a,能耗和CO排放量分别减少5.09×10kW/a 和4.82×10kg/a。脱轻组分塔和异己烷塔的最佳采出量分别在180~196kg/h 和2790~2800kg/h 范围内,适当增加正己烷塔的采出量有利于增加年毛利润;脱轻组分塔、异己烷塔和正己烷塔的最佳回流比分别在[30,32]、[8.5,8.8]和[9.5,10.5]范围内。

