基于线性规划模型的订购与运输方案研究

胡慧旦，张海波，林天舒，周洪鹏

（台州学院 电子与信息工程学院，浙江 临海 317000）

0 引言

近几年，国内外对货物订购和运输的策略研究虽不是很多，但较为深入，一些建模比赛也都涉及了该类问题。在对该类问题的研究和解决中，大多数学者都运用了遗传算法和线性规划来进行求解和优化。此外，在研究订购方案时，大多已有的模型中都融入了对供应商的供货能力、运输能力等限制因素的考虑，在满足企业计划要求的基础上，确定使企业订购费用和存储费用最小的采购计划。伊朗德黑兰沙希德大学的Patoghi Amirhosein提到了一种新的数学模型，该模型用于多站点运输，旨在最大限度地降低项目总成本以及项目的完成时间。文中考虑了全单位折扣政策和多模式的订购问题，根据原有的研究成果，结合更多现有数据，对研究内容进一步完善，为有供货和订货需求的企业提供相关的运输方案。

1 问题分析

本文基于2021年全国大学生数学建模竞赛C题中提供的数据：根据近5年402家供应商每周不同材料的供应情况，需要确定体现供货特征的指标。供货特征可以通过企业对供应商的依赖度、供应商对企业供货的稳定性以及供应商的最大供货能力和履约率来表示。首先，通过企业的订货量找出对企业订购影响最大的供应商，再通过观察这些订货量，找出对企业影响最大的几家供应商。为了表示出这4个指标，可以通过近5年在各个供应商进货的次数比（某个供应商提供一类原材料的次数与总的订购该类原材料的次数的比值）、各个供应商供货的总量（该供应商提供的5年的总供货量）、各个供应商提供的原材料的量在该类原材料总量中的占比、各个供应商一周的最大供货量以及对供应商的满意度来完成。其次，通过给定数据计算出次数比、进货总量和占比。对于企业对各个供应商满意度的评定，可通过确立一个模糊函数来实现。最后，针对这4项指标确定4个约束条件。由于是为企业选择50家最佳的供应商，最大程度满足企业的需求，因此可运用多目标线性规划的思想，根据企业订货量的数据选出50家最重要的供应商。

由于生成同样体积的产品，需要消耗的三种类型原材料的体积各不相同。为了能够直观且方便地对订购方案（不同类型的原材料组合）进行计算比较，需要将供应商供应的原材料和企业需要的订单量全部转化为产能，然后再进行计算。首先，将供应商各自240周的原材料供应量转化为相应的产能，接着根据量化后的产能数据运用BP神经网络预测出未来26周的产能。同样，将企业每周的A、B、C类原材料订单量也全部转化成产能，求出企业每周的产能需求，然后预测出未来26周的企业订购的产能。为了消除个别较低产能的供应商的影响，去掉产能小于100的供应商。通过求出筛选后的各个供应商的平均产能并对其进行降序排序，将平均产能最大的供应商进行累加，直到所得的产能之和大于最大需求量，由此求出重要的几家供应商。之后通过线性规划确定企业需要的供应商，求出未来26周每周最经济的原材料订购方案。接下来预测未来26周的不同转运商的损耗率，运用线性规划制订出损耗最少的转运方案。最后再根据订购方案和转运方案从对企业的稳定性和成本两方面进行效果分析。

1.1 重要供应商筛选模型

根据问题分析，需要确定5个供货特征来进行分析，因此给出该企业在各个供应商进货的次数比、各个供应商进货的总量、各个供应商提供的原材料的量在该类原材料总量中的占比、各个供应商一周的最大供货量以及对供应商的履约率。接着，用这5个供货特征对企业的订单量表格依次进行求解，建立整体求解流程图模型，如图1所示，并对流程图模型中的指标依次进行建立。

图1 最佳供应商筛选流程图

首先，分别对402家供应商不同周供货量进行分析，通过数据分析找出相应的供货规律，由此找出对企业的订货量产生较大影响的供应商。在402家供应商收到的订货量周期图中可以初步看出S140，S307，S108，S139这4个供应商具有周期性且供货能力较大［1］，如图2～5所示，因此这4个供应商可以提前确定为 4家对企业生产比较重要的供应商。而 S374，S348，S330，S308，S201，S151，S126这 7家供应商不具有周期性且相应的供货能力较小，因此可以将这7家供应商预先淘汰。

图2 企业向S140的订货量周期图

图3 企业向S307的订货量周期图

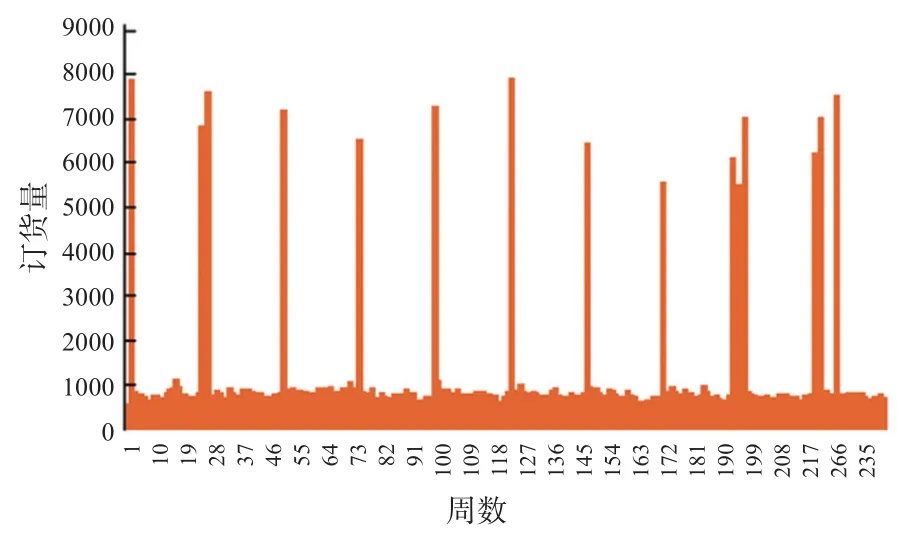
图4 企业向S108的订货量周期图

图5 企业向S139的订货量周期图

1.1.1 依赖度

依赖度是指企业与供应商之间的依赖程度，依赖度越高，说明该供应商对商家来说越重要。依赖度可以通过该企业各个供应商的次数比和各个供应商供货的总量来描述，供应商的总量为该供应商提供的5年总供货量，供应商的次数比为某个供应商提供一类原材料的次数与总的订购该类原材料的次数的比值，定义函数为：

由此计算出企业对不同商家的依赖度，通过依赖度判断供应商对企业的重要性。

1.1.2 单次最大供货量

供应商的单次最大供应量可以反映供应商对企业的供货量的重要程度。供应商单次可供货的数量可以用各个供应商一周的最大供货量gmax来表示，即

1.1.3 稳定性

稳定性表示不同供应商对企业供货的稳定程度，稳定性越高，则表示该供应商对企业越重要。供货的稳定性可以用各个供应商提供的原材料的量在该类原材料总量中的占比表示，公式为：

A,B,C为供应商提供的原材料。

1.1.4 履约率

供应商生产的效率及完成程度可以通过对供应商履约率的求解来表示。令矩阵D(i,j)表示企业在5年内每周的订货量的矩阵，矩阵G(i,j)表示各个供应商在近5年内每周供货量的矩阵。通过供货量与订货量的差值来判断履约率，建立如下模型：

表示供应量g与订单量d之间的差值为c，企业对供应商的履约率会随着差值的变化而变化，因此假设履约率函数由两段二次函数构成。当差值c=0时，没有考虑到损耗率，故履约率为0.5，构造函数分别为：

当差值占订货量的1%时履约率为1，即y1过（1，1）和（0，0.5）这两点；当差值为订货量的5%时，供应量远大于需求量，供应量过多，会提高企业的成本支出，则履约率为0。因此y2过（1，1）和（5，0）这两点，由此求出：

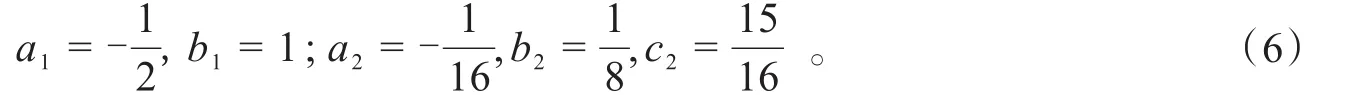
综上可确定每周供应商的履约率为：

由于中位数最能反映一个量的中间水平，因此根据求出的除履约率外的4项指标的值进行中位数求解，按中位数大小进行依次筛选，选出满足条件的供应商［2］。再利用第1次筛选出的供应商进行第2次筛选。因为第1次筛选掉的供应商的履约率几乎全为0，故第1次筛选对第2次筛选不会造成影响，该次筛选先按照履约率进行降序排序，然后选择前50家供应商。

1.2 重要供应商筛选模型的求解

模型建立中的5个不同的指标分别反映了供应商不同的生产特征，如图6所示。

图6 指标对应的生产特征

1.2.1 依赖度的判定

根据各个供应商的次数比公式求解出次数比，如图7所示，各个供应商供货的总量如图8所示。

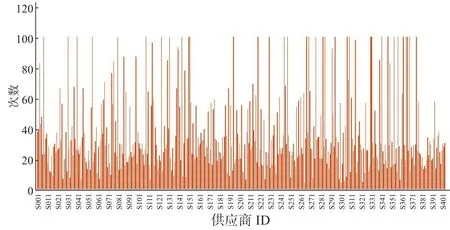
图7 402家供应商各自供应的次数

图8 402家供应商各自供应的总量

1.2.2 单次最大供货量的求解

供应商一次性最多可供货的数量可以通过各个供应商一周的最大供货量gmax来描述，如图9所示；供应商最大供应能力如图10所示。

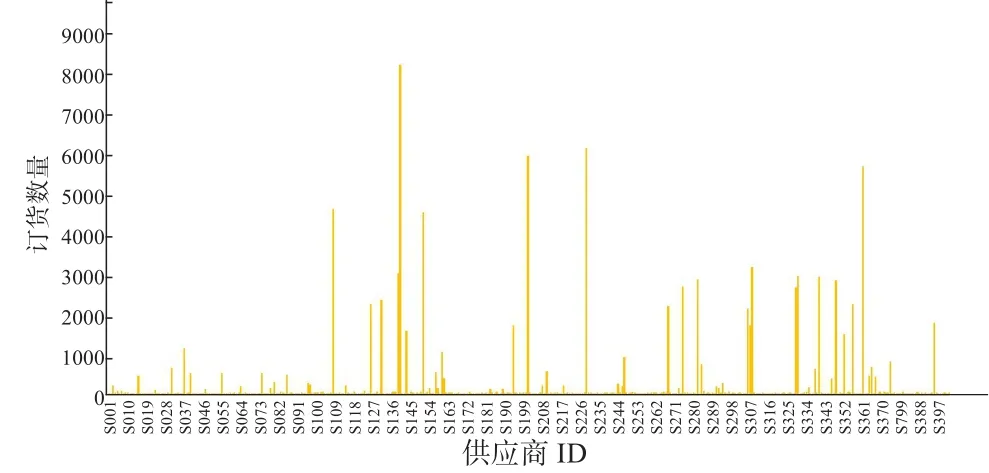
图9 402家供应商订货数量

图10 402家供应商最大供应数量

1.2.3 供应商供货的稳定性

供货稳定性是指各供应商提供的原材料的量在该类原材料总量中的占比。

1.2.4 供应商生产的效率及完成程度

供应商生产的效率及完成程度可通过对供应商的满意度来表示，如图11所示。接着，求解近5年各个供应商进货的总量、次数比、供货稳定性及一周的最大供货量这4个指标的中位数，如表1所示。

图11 402家供应商的平均满意度

表1 4个指标的中位数

根据表中4个中位数值对供应商进行筛选，选出4个指标均大于中位数值的供应商，并以此条件完成第1次筛选，共选出117家满足条件的供应商。接着根据履约率进行计算，算出近5年对各个供应商的履约率的平均值。最后根据满意度平均值的降序排序选出了50家供应商，如表2所示。

表2 50家供应商

根据如此的筛选过程可以保证所选择的供应商能够在满足企业的进货要求的同时使得企业能够获得最大的满意度，选择企业依赖度和稳定性最大的供应商来保证企业的正常生产。

1.3 供货产能和订购产能的预测

根据数据预处理后得到的供应商供货产能和企业订购产能，运用BP神经网络预测未来26周的供应商供应产能和订货产能［3-4］。BP神经网络通常采用Sigmoid可微函数和线性函数作为网络的激励函数，而由于网络的输出归一化到［-1，1］范围内，因此预测模型选取S型对数函数Tansig作为输出层神经元的激励函数。BP神经网络训练用的是MATLAB神经网络工具箱，具体实现步骤为：①读取所需预测的数据集，放入空矩阵内作为训练样本。②将训练样本数据归一化后输入网络，设定网络隐层和输出层激励函数分别为Tansig和Logsig，网络训练函数为Traingdx，网络性能函数为Mse，隐层神经元数初设为6。③设定网络参数。网络迭代次数epochs为100次，期望误差goal为0.00000001，学习速率lr为0.01。④训练网络。训练的具体过程分为2个阶段：第1阶段是信号的前向传播，从输入层经过隐含层，最后到达输出层。在这个过程中，我们根据输入样本给定的初始化权重值和偏置项的值，计算最终输出值以及输出值与实际值之间的损失值。如果损失值不在给定的范围内则进行反向传播的过程，否则停止初始化权重值和偏置项的更新。第2阶段是误差的反向传播，从输出层到隐含层，最后到输入层，依次调节隐含层到输出层的权重和偏置、输入层到隐含层的权重和偏置，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。最终可以预测出未来24周的企业的订购量产能。训练、验证和测试结果如图12～15所示。

图12 未来24周企业订购量产能预测图

图13 均方差训练次数的变化规律

图14 BP神经网络各阶段的训练图像

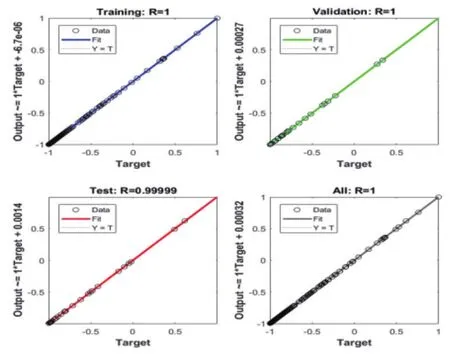
图15 各个样本集和总体的相关性分析

根据预测出的未来26周的企业订货量，可以看出订购量产能基本稳定在3万与4万之间。运用同样的方法可以预测出供应商在未来26周的供货量的产能。为了减少个别产能的影响，删去供货产能小于100的数据。接着，求出各个供应商在未来24周的平均产能。根据供应商供货平均产能由大到小进行排序，由于当供应商提供的原材料总和大于最大需求量时即为至少需要的供应商数量，因此将产能由大到小依次累加，直到累加的和大于5万时停止，共计27家，如表3所示。

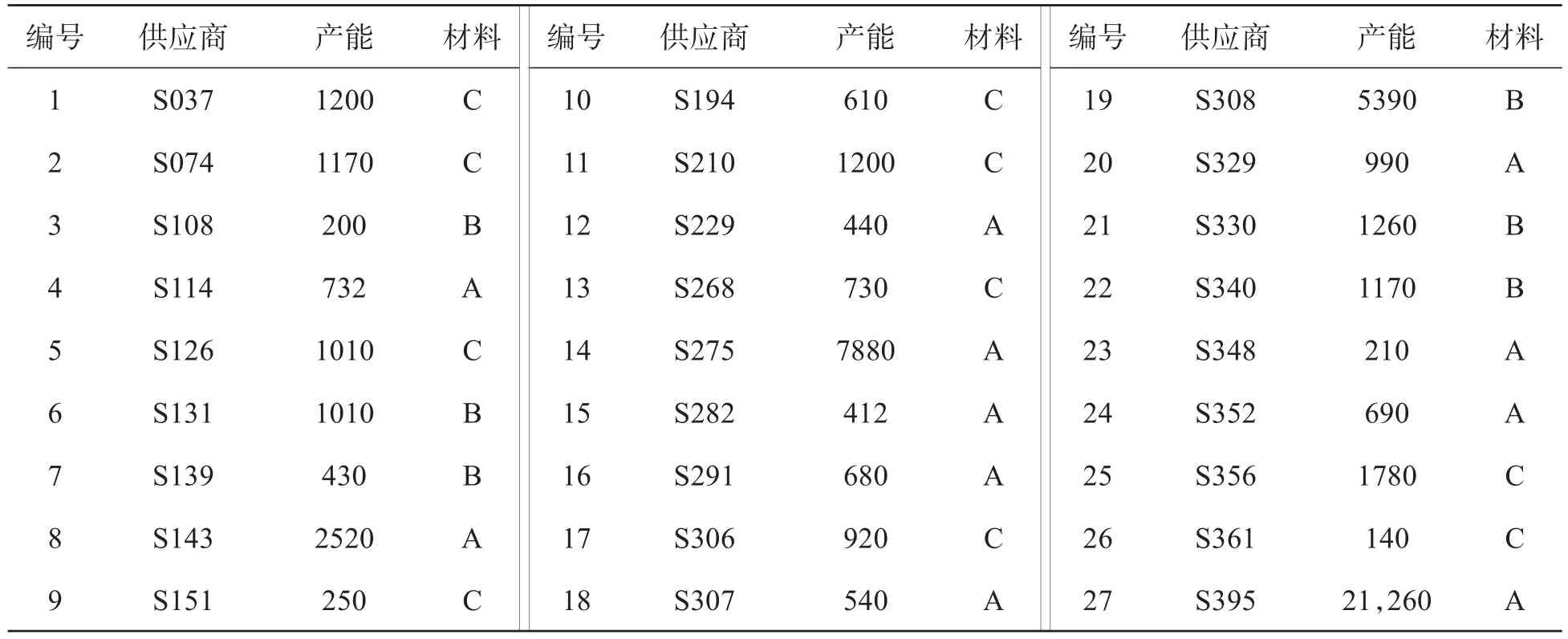
表3 供应商在未来24周的平均产能

1.4 原材料订购方案的线性规划模型

为了确定未来24周每周最经济原材料订购方案，运用多目标线性规划来制定原材料订购方案。建立目标函数

其中，根据选出的27家供应商已经确定出每家供应商可提供的原材料的种类，则

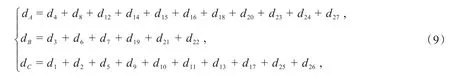
该目标函数表示能够同时满足企业的四个目标。

1.5 熵权法求系数

假设有27个要评价的对象，构成的正向化矩阵如下：

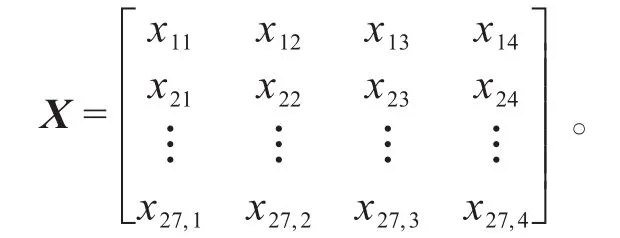
将对其标准化的矩阵记为Z，Z中的每一个元素表示为：

若矩阵Z中存在负数，则对矩阵X进行如下标准化得到Z͂。首先定义

接着，将相对熵计算中用到的概率来表示第i项指标下第j个样本所占比重。上一步求得的非负矩阵为：

下一步计算概率矩阵P，其元素

其中，每一个指标的概率和等于1。最后通过计算各指标的信息值和效用值，通过归一化得每个指标的熵权。信息熵计算公式如下：

其中，为使得信息熵始终位于［0，1］，因此该式子要除以ln(n)。ej越大则表明第j个指标的信息越少。

定义信用效应值为kj=1-ej，信息效应值越大，其对应的信息就越多。最后，将其归一化可求得每个指标的熵权为：

运用该方法计算出指标的系数λ1,λ2。

1.6 多目标加权线性规划

计算出两个指标的系数后，可运用多目标加权线性规划，确定其目标函数为：miny=λ1×(1.2dA+1.1dB+dC)+λ2∑∑dij(1-tij)。根据A，B，C采购的单价以及每家转运商的运输能力不超过6000 m3/周，各个供应商供货不超过最大供货能力，并且供应商的接收量等于需求量时可建立如下条件：

其中：Qi表示不同周的需求量；Mij为转运量。通过求解该线性方程组，将24周的不同需求量代入Qi，即可解得24周下的最优订购方案。

2 模拟仿真

方案的实施效果可以通过随机模拟的原料总消耗费用与文中制订的订购方案和转运方案产生的费用进行比较。本文采用仿真模拟随机取100种产能，模拟100次得出随机模拟可能产生的24周的总费用。如果随机模拟产生的总费用大于文中制订方案下产生的费用，则说明制订的订购方案和转运方案实施效果较好。

建立如下模型：随机取产能计为Wi，将其随机分配给选出的27家供应商xi，每家供应商分到的产能计为wij；接着根据每家供应商所生产的原材料种类将产能转换为对应的原料，xAn表示A类原材料在第n次仿真模拟时的24周的总和，xBn表示B类原材料在第n次仿真模拟时的24周的总和，xCn表示C类原材料在第n次仿真模拟时的24周的总和，由fn=1.2xAn+1.1xBn+xCn计算出每次仿真模拟方案下的费用。当n=100时即进行100次仿真模拟，将100次的模拟费用求解平均值，得到仿真模拟下24周的费用，然后进行如下比较，如表4所示。

表4 仿真结果

续表

分析表4中的差值可得仿真模拟下费用均大于原制订方案下的费用，因此可以得出制订的方案实施效果较好，能够帮助企业的经济可持续，其是在较少费用下实现损耗最小的转运方案。

3 结语

本文采用线性规划方法，对原材料的订购和运输方案进行研究，并通过模拟仿真的方法对得到的方案进行评估。通过仿真结果可以发现本文给出的方案实施效果较好。但本文的方法没有考虑到各供应商之间的距离和仓储的实际存储能力，在实际应用中这些因素对订货方案和运输方案的制订都有较大的影响，综合考虑这些因素的影响将是对该问题进一步研究的方向。