思维能力:小学数学有效使用教材的价值旨归
白丽琼(甘肃省庆阳市镇原县南区小学)
教材是教学的重要依据和资源,但是也常常成为一些教师的束缚,部分教师依赖教材,将教材奉为不容置疑的权威。教材既不是不能质疑的权威,也不是可以随意删减的素材,需要教师在充分研读中有效使用。
一、在对比辨析中培养思维的准确性
小学六年级要学习分数乘除法的应用,很多学生对于简单的计算都能熟练计算,但是一旦涉及到乘除法的图形表示就经常不知所措,因此笔者尝试将这部分教材作了一定的有效编排,以期能更加合理地使用教材。
案例1:用图形表示分数乘法
教材原题:图1练习分数的乘法,

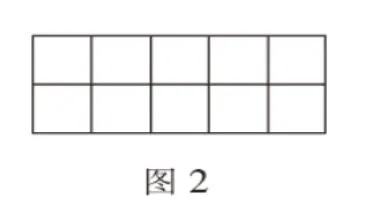
图2练习分数的除法。
图1根据题意学生能很快找到涂色阴影部分占整张纸的,第一张图斜线占中的,第二张图斜线占的,由此分别列式和。
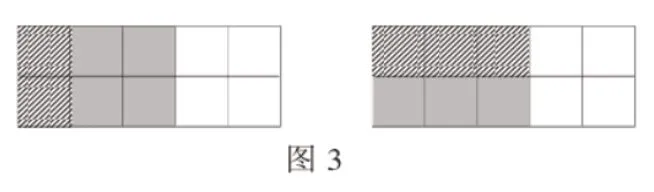
图2原题为:在图2中用阴影表示出,再说一说里有几个,有几个,根据题意可以画出如图3的示意图,就可以一目了然地得出里有3个,有2个。
教材中这样的设计可以帮助学生形象直观地了解分数乘法和除法的意义,通过先涂阴影,再数格子的做法非常清晰明了,并且通过示意图对于分数乘除法的计算也能做到简明扼要。教材仅仅这样中规中矩地使用,没有发挥教师对这一知识点的思考和设计,也就欠缺了对学生思维的训练,一旦在试题中涉及到乘除法的混合运用,学生又觉得困难重重,所以笔者进行了如下的设计:
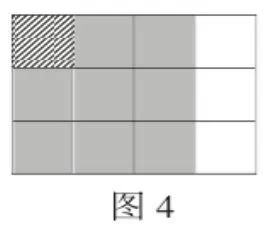
两道算式分别从两个角度表达了分数乘除法的意义,第一道算式表示的是图形4中斜线部分占阴影部分的比例,第二道算式则表达了在阴影部分中有几个斜线方格,可以说这样的设计弥补了教材中对于分数乘除法的混合运用。
本例中教师不仅抓住了学生容易产生的困惑和矛盾点,而且改变教材中全部采用正向思维训练的方式,通过逆向思维给出试题,由学生进行讲解意义,进行了知识的反向运用,大大拓展了思维的力度。
二、在动静变化中培养思维的发散性
教师要把握学生思维发展的动向,将静态的试题进行动态的展示,鼓励学生动手实践、自主探究、合作交流,在动态的探索中达到高效的学习效果。
案例2:计算图形重叠部分面积
教材原题:观察下图,求两个正方形重叠阴影部分的面积,正方形边长如图所示。
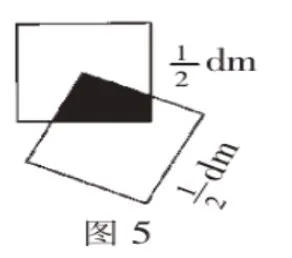
面对不规则图形的求解,需要学生发挥想象建立联系,完成思维建模的过程,只有让静态图形立体化才能充分发挥学生的想象空间。因此,在教学中教师充分发挥学生合作交流,自主探究的主动性,引导学生通过拆分、添补等方法,自己动手实践,相互交流,让学生发挥自己的创意和方法。学生经过思考的答案也让教师欣喜万分,展示如下:
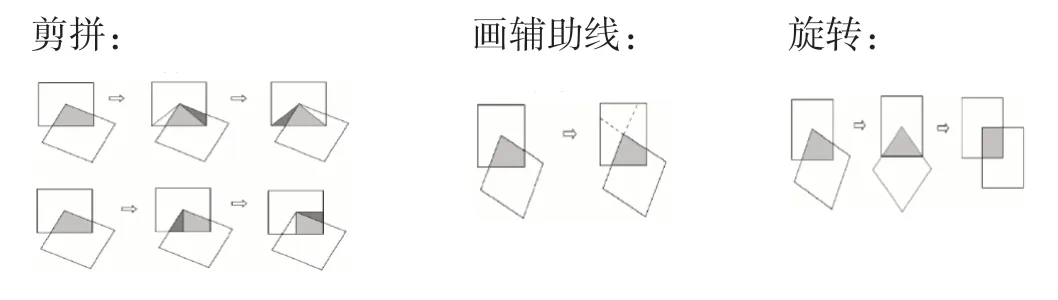
在动手的实际操作中,学生发现看似无解的试题,其实通过转化的思想都能找到相同的答案。本例中教师没有局限学生的思路,选择让学生思考在前,讨论在前,教学在后的方法,充分锤炼了学生思维的发散性,体现了教师对教材的灵活把控。
三、在知识拓展中培养思维的深刻性
因此课堂教学不应是单一知识点孤零零地教学,需要注意前后联系,知识难度螺旋上升,不断总结规律,探索本质,在一次次解决问题的过程中,不断拓展知识的广泛度,训练思维的深刻性。
案例3:分数的计算
教材原题:

本题是在分数加减法基础上的一道进阶题,如果教学中只是就这道题而讲就失去了教材如此安排的意义,因此可以联系之前学过的知识进行联系和对比,观察发生了怎样的变化,会有意想不到的收获,所以笔者的教学过程是这样安排的:

师:请大家计算图7中的算式,有没有同学能说一说你的计算步骤呢?
生1:异分数的加减法我们需要先通分再进行计算,经过我刚才的观察,我发现上面的算式分母都有一个特点,分母是互质的。
师:是的,这里的分数加减法中的分母都为互质,分子都为1,那么它们的计算结果有什么特点呢?
师:很好,这个规律不知道同学们是否还有印象,其实我们在五年级的时候已经学习过了。那么我们今天就要来做一做进阶题,在分数的乘法中又蕴含着怎样的规律呢?请大家看图6思考。
师:同学们发现数学的有趣和奥秘了吗?在数学之中还藏着很多这样有趣的东西,那么你们能不能模仿上面的题目,也写出一些含有这些规律的题目呢?
师:看来同学们已经掌握了这个秘诀了,但是老师想要找到更加普遍性,放之四海而皆准的规律,该如何总结呢?
生5:(学生开始热烈讨论,最后得出答案。)我们可以这样总结:
本例中教师充分利用了教材知识,并在此基础上进行拓展和编排,在教师的精心设计中学生沉浸其中,积极思考,感受到了数学的趣味性,使他们的数学学习能够乐在其中。

