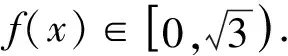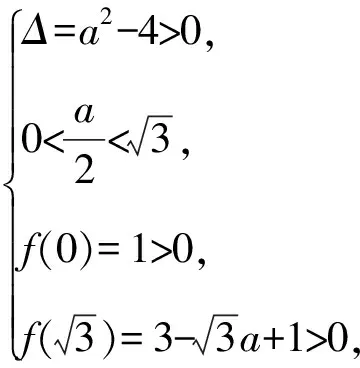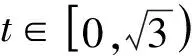求三角函数中参数的取值范围的几种题型
田素伟
(上海市泥城中学 201300)
常考常新的三角函数问题,一直是高考的一个重点,近年来,数学高考中出现了一些重视基础,考查能力的新型试题,特别是在三角函数中含参数的问题更是精彩纷呈,如何求这类三角函数中参数的取值范围?下面就常见的几种题型分别举例说明.
1 构造函数解不等式
例1已知实数a满足sina2+sina>a2+a,则a的取值范围是____.
解析将sina2+sina>a2+a变形为
sina2-a2>-(sina-a).
构造函数f(x)=sinx-x,
所以sina2-a2>-(sina-a)可化为
f(a2)>-f(a).
又因为f(-x)=sin(-x)-(-x)=-(sinx-x)=-f(x),所以f(x)为奇函数.
所以f(-a)=-f(a).
所以f(a2)>f(-a).
由f′(x)=cosx-1≤0知,f(x)在R上为减函数.所以a2<-a.解得-1 所以a的取值范围是-1 评析本题是通过观察题中式子特征构造函数f(x)=sinx-x,然后利用函数的性质解不等式. 解析把eα-eβ=cosα-2cosβ变形为 eα-cosα=eβ-cosβ-cosβ, 所以eα-cosα=eβ-cosβ-cosβ可化为 f(α)=f(β)-cosβ. 因为f(x)=ex-cosx,则f′(x)=ex+sinx>0. 所以f(β)-f(α)=cosβ>0. 所以f(β)>f(α).所以β>α. 解析由f(x)=x2021+x,显然f(x)为奇函数,且单调递增. 因为f(msinθ)+f(1-m)>0恒成立, 即f(msinθ)>f(m-1)恒成立. 所以msinθ>m-1恒成立. 设t=sinθ,则t∈[0,1]. 所以msinθ>m-1可化为mt>m-1. 所以mt-m+1>0. 这里有两个变量m和t,因为t的取值范围已经确定,所以确定以t为主变量,把不等式转化为关于t的函数. 设f(t)=mt-m+1, (1)当m=0时,此时f(t)=1>0符合题意; (2)当m≠0时,函数f(t)=mt-m+1是关于t的一次函数, 解得m<1且m≠0. 综上可知,实数m的取值范围是(-∞,1). 评析本题利用函数的性质转化为关于两个变量m和t的不等式,因为t的取值范围已经确定,所以确定以t为主变量,把不等式转化为关于t的函数,一般情况下含两个变量m和t的不等式,如果其中一个变量的取值范围能确定,那么就以这个变量为主变量,另外一个变量作为参数. 评析本题是含参数的三角不等式的恒成立问题,不等式的恒成立问题一般转化为函数的最值问题.一般方法是不等式同解变形为a>f(x)或者a 因为t=cosx+sinx,所以t2=(cosx+sinx)2. 所以sin2x=t2-1. 不等式2sin2x-a(sinx+cosx)≤0可化为 2(t2-1)-at≤0. 所以本题可转化为 评析本题通过换元把三角问题转化为给定区间上的不等式恒成立问题,再转化为函数的最值问题. 图1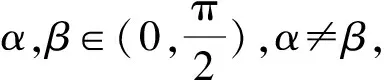
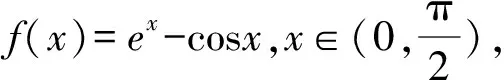

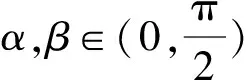
2 双变量问题先确定主变量


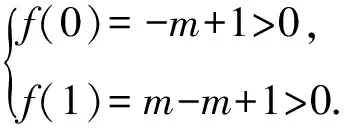
3 利用函数单调性求解
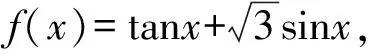
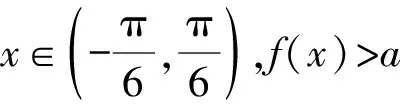
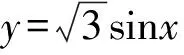

4 利用换元转化为函数问题
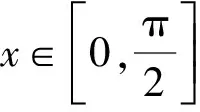
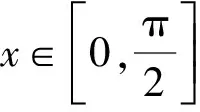
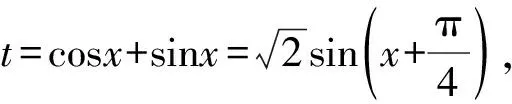
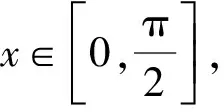
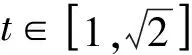
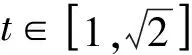
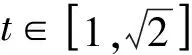

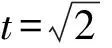
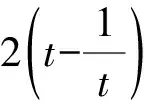
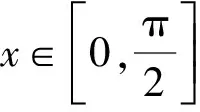
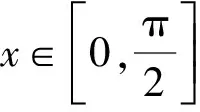

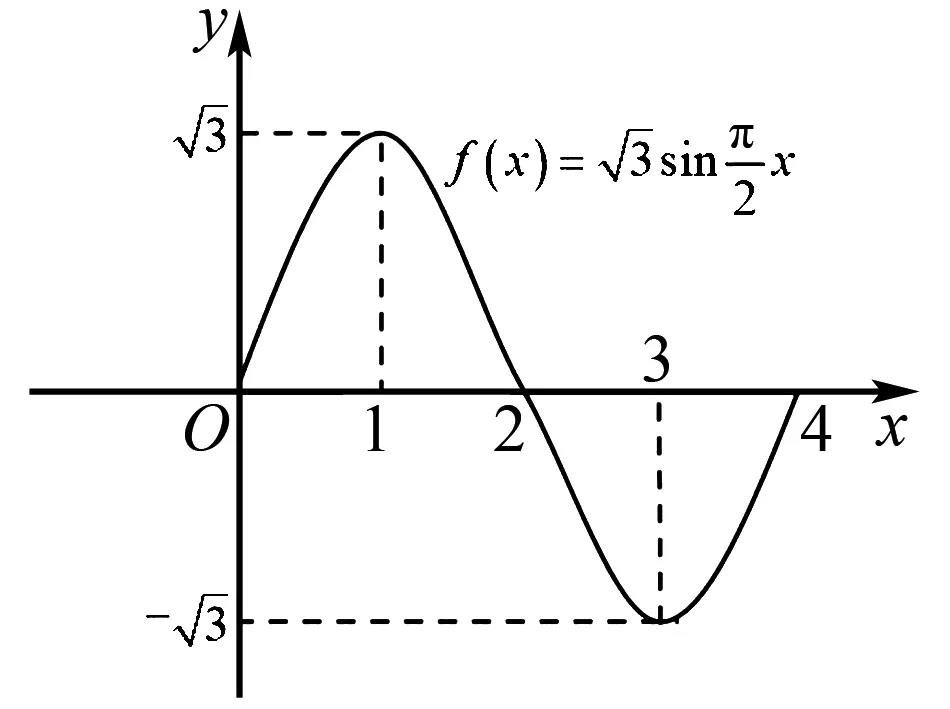
5 数形结合求解