追溯“源头” 拨开云雾见“真身”
——例析“与圆相关的最值问题”
陈 龙
(湖北省水果湖高级中学 430071)
源题1已知圆C:(x-4)2+(y-3)2=25,求过点M(2,1)的直线l被圆C截得的最短弦长和最长弦长.
解析因为(2-4)2+(1-3)2=8<25,
所以点M在圆C内.


图1

变式已知C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0,求直线l被圆C截得的弦长的最大值和最小值.

源题2已知点P(x,y)是圆C:(x-3)2+(y-3)2=4任一点,求点P到直线l:2x+y+6=0距离的最大值和最小值.



图2
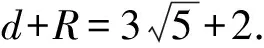
点评此题属于考查直线与圆相离时圆上点到直线距离的最值问题.最大值为d+R,最小值为d-r.
变式1由直线l:y=x+1上的一动点P向圆C:(x-3)2+y2=1引切线切于点D,求切线PD长的最小值.


图3 图4
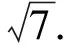
变式2 已知点P为直线y=x+1上的一动点,过点P作圆C:(x-3)2+y2=1的切线PA,PB,A,B为切点,求cos∠APB的最小值.
解析由图4知cos∠APB=cos2∠APC=1-2sin2∠APC,


源题3已知实数x,y满足x2+y2-4x+1=0.

(2)求n=y-x的最大值和最小值;
(3)求t=x2+y2的最大值和最小值.
解析(1)因为点P(x,y)满足圆C:(x-2)2+y2=3方程,即点P在圆C上.


图5 图6
(注:利用点C到直线y=kx距离等于半径求出相切时的k值)


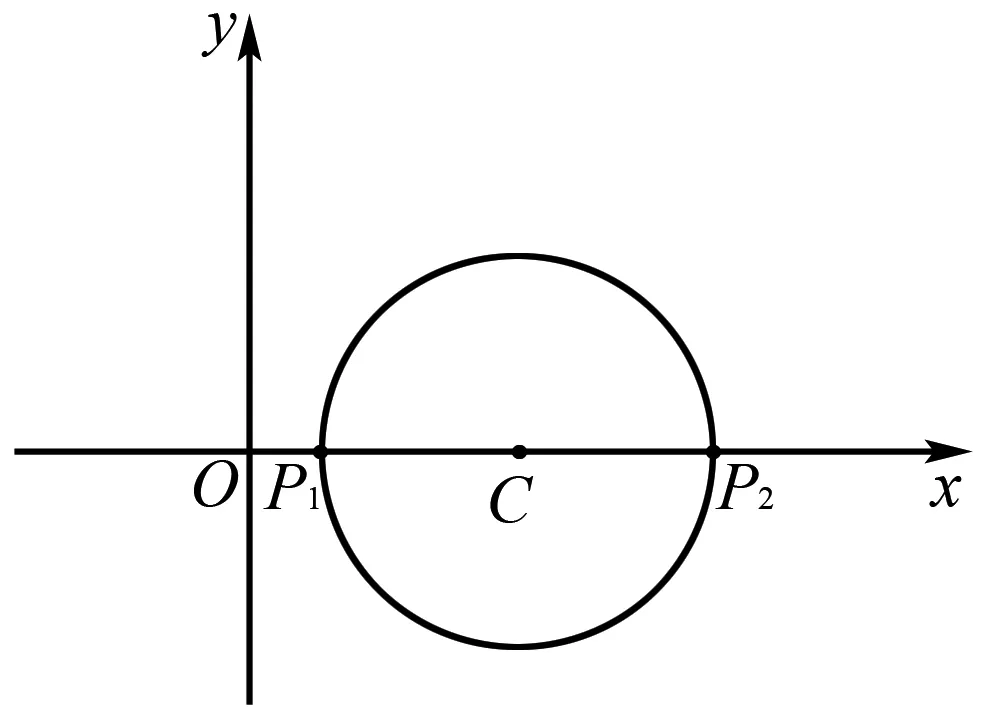
图7
点评此类题属于考查直线与圆相切时相关的最值问题.处理时要考虑所求式子的几何意义.


变式2若实数x,y满足x2+y2+2x-4y=0,求x-2y的最大值.
解析(x+1)2+(y-2)2=5,

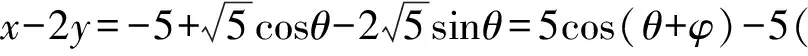
所以当cos(θ+φ)=1时,(x-2y)max=5-5=0.故x-2y的最大值为0.
点评本题是典型的用圆的参数方程解决的题型,利用圆的参数方程将所求式转化为三角函数求最值,利用辅助角公式即得最大值,此法在后续圆锥曲线的学习中会有所推广.
变式3平面上有两点A(-1,0),B(1,0),P为圆x2+y2-6x-8y+21=0上的一点,试求S=|AP|2+|BP|2最小值.
解析把已知圆的一般方程化为标准方程,得
(x-3)2+(y-4)2=4.
设点P的坐标为(x0,y0),则
S=|AP|2+|BP|2
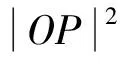
要使S=|AP|2+|BP|2最小,需|OP|最小,即使圆上的点到原点的距离最小.
容易知道|OP|min=|OC|-r=5-2=3.
所以Smin=2(32+1)=20.
点评设P(x,y),使要求的式子转化为求圆上的点到原点的距离问题,利用数形结合法求最值,实质上是利用初中学过的“连接两点的线段中,直线段最短”这一性质.
变式4过直线y=1上一点P(x,y)作圆(x+1)2+(y+1)2=1的切线,求切线长的最小值.


以上列举了几道“源题”和若干变式题目,说明了一些看似复杂的题目的真身依然是我们熟悉的知识点.
圆的知识在初中与高中都要学习,是一典型的知识交汇点.现在的数学高考非常重视初高中知识的衔接问题,所以同学们在处理与圆有关的小题时,一定要数形结合,多联想一下与之有关的平面几何知识,以免“小题大作”.由于圆的对称性,在与圆有关的最值问题中,应把握两个“思想”:几何思想和代数思想.所谓几何思想,即利用圆心,将最值问题转化为与圆心有关的问题.所谓代数思想,即利用圆的参数方程.同时,由于最值问题从代数意义上讲和函数的最值联系紧密,因此在解题过程中灵活地应用函数、不等式等代数思想使问题代数化、简单化也是需要注意的.

