改进SVM不平衡数据分类的IGWOSMOTE方法*

马汉达，朱 敏

(江苏大学计算机科学与通信工程学院,江苏 镇江 212013)

1 引言

由Vapnik[1]提出的传统分类器支持向量机SVM(Support Vector Machine)，具有坚实的统计学理论基础、简易的实现方式以及优秀的泛化能力和分类性能，目前在信用评估[2]、文本分类[3]和人脸识别[4]等领域中应用非常广泛。SVM在处理多分类[5]问题时，往往因误分及不可分的问题导致最终分类精度不乐观，其中误分的根本原因是少数类和多数类样本分布失衡，少数类即某个类样本规模远小于其他类的样本规模，反之，样本规模较大的则称为多数类，学术界普遍将少数类和多数类也分别叫做正类和负类。不对称的数据量造成了分类超平面对负类的倾斜，而待测样本被所有子分类器都判为负类则是导致不可分的原因。因此，如何提高SVM对于不平衡数据的识别率及整体分类准确率是当前数据挖掘领域的一大难点。

少数类合成过采样技术SMOTE(Synthetic Minority Over-sampling TEchnique)[6]从数据层角度出发，通过数据集重构的方式来均衡少数类和多数类的样本数量，以线性插值为原则随机复制少数类样本，这样可以避免算法过拟合，从而更有利于SVM分类器的学习。众多学者的研究表明，SMOTE算法在不平衡数据分类问题上能取得良好的分类效果。Chen等[7]使用SMOTE改进SVM算法以适用于混合类型和不平衡数据，实验表明使用了SMOTE方法的SVM分类器在平均准确率、查准率和查全率上均能取得不错的分类结果。Prachuabsupakij等[8]提出的KSMOTE(K Synthetic Minority Over-sampling TEchnique)方法将数据集分为2个子集，并分别对这2个子集使用过采样和欠采样方法，构建SVM的“一对一”和“一对多”分类模型进行预测实验，最终在ROC曲线下的面积AUC和F_measure这2个指标上体现了该方法的有效性。古平等[9]将SVM作为元分类器，基于错分原理提出新的混合采样方法，将样本划分为危险样本和安全样本，并分别进行样本约除和SMOTE过采样，对比实验表明新方法在提高少数类识别率上具有较好的性能。然而，在实际中对少数类样本的识别率往往易受到噪声样本[10]的干扰。这些噪声可能是原数据集中的噪声样本，也可能是基于噪声样本再次生成的新噪声样本，都会使少数类更不易被识别到，从而造成分类精度更低的局面。另外，SMOTE算法对每一个少数类样本均采用了相同的合成方式及采样倍率，因此可能会产生偏离或者远离决策域的无效样本[10]，这样既无益于分类器学习也加重了算法运行负担。目前已有很多学者基于这2点对SMOTE算法进行改进,Han等[11]提出的Borderline-SMOTE方法只对处于决策域的正类样本进行过采样，主要是对当前正类样本和与其相邻的正类与负类样本的个数进行比较，若相邻正类样本数多则表明该样本处于决策域内，反之则视为无效样本予以摒弃。刘雨康等[12]引入分区的理念把样本空间划分为密集区(即多数类)与稀疏区(即少数类)，先后将传统SVM算法和K-最近邻算法用于密集区和稀疏区的分类，使得各SVM子分类器中的噪声样本数明显减少，这样不仅分类更准确，而且算法运行时间更短。霍玉丹等[13]提出了GASMOTE(Genetic Algorithm Synthetic Minority Over-sampling TEchnique)过采样方法，利用GA循环优化输出最优的采样倍率取值组合进行样本过采样，使SMOTE采样倍率取值具备一定的灵活性。以上研究均对SMOTE的局限性和盲目性做出了相应改进，但仍存在以下缺陷：

(1)当样本规模较大时，忽略了特征维度对样本识别的贡献能力[14]。通常情况下少数特征对样本的识别率贡献较大，存在冗余特征时则对样本识别贡献较小。

(2)忽略了SVM中有关参数的取值在参与采样过程中的相关性和重要性，一般可以为少数类和多数类分配不同的惩罚权重C，例如当少数类样本远少于多数类样本时，可为少数类样本赋予较大的C值，但是这种操作可能使初始数据的概率分布发生偏离。

本文针对以上问题做出相应改进。首先，使用改进的灰狼优化算法IGWO(Improved Gray Wolf Algorithm)[15]进行SVM的参数寻优及特征选择，将二者作为构成灰狼初始种群的因素之一，并为其设计适应度函数，通过灰狼优化过程获得达到最佳分类准确率的最优参数组合及特征向量子集，为少数类样本和多数类样本分别赋予较大和较小的惩罚权重，从而避免原始数据分布出现严重偏差。其次，引入随机的采样倍率组合参与灰狼种群的初始化过程，利用IGWO的自适应搜索能力输出最佳采样倍率组合。本文提出的基于改进灰狼算法的过采样方法——IGWOSMOTE(Improved Gray Wolf Optimization Synthetic Minority Over-sampling TEchnique)，旨在缓解因初始数据中存在的冗余特征使得少数类样本易被误判为噪声样本，造成负类样本规模更小的现象，以及改善因人为定义采样系数而导致SMOTE算法生成无效样本的问题。最终减小传统SVM多分类问题受不平衡数据的影响，提升对少数类数据的识别率及SVM的整体分类准确率。

2 相关方法

2.1 支持向量机

s.t.yi(ωxi+b)≥1-ξi,i=1，2，…，l

(1)

其中,ω为超平面的法向量;b为超平面的偏置;ξi为松弛变量;C为惩罚因子。

以径向基核函数为例，在数学模型中可通过式(2)和式(3)所示的目标函数和决策函数的优化来描述寻找最优分类超平面的过程[5]，式(4)给出了其约束条件。

目标函数：

(2)

决策函数：

(3)

约束条件：

(4)

2.2 SMOTE算法

为了解决不平衡数据的分类问题，Chawla等[6]从合成少数类样本的角度出发,设计了一种过采样算法。SMOTE算法的思想是，采用线性插值的方式在近邻少数类样本之间手动增加新的少数类样本个数，从而尽可能达到数据平衡的状态，算法步骤如下：

(1)对于每个少数类样本S，利用欧几里得距离计算出S与其他少数类样本间的距离，正序排列得到前k个近邻样本，k值一般设为5。

(2)根据采样倍率N，从k个近邻中随机选取一个样本S′,在S与S′之间插入采用式(5)所示的线性插值公式合成的新样本Snew。

Snew=S+(S′-S)×rand(0，1)

(5)

其中，rand(0，1)为0到1之间的随机数。

(3)将新增的样本加入到原训练集中再次进行分类器学习。

2.3 灰狼优化算法

Mirjalili等[15]受灰狼群体活动中的领导阶层和捕食体制启示，将狼群分为4种阶层，其中以α狼为首领，β狼次之，δ狼又次之，其余底层狼群为Ω，由4种灰狼共同完成狩猎过程。在灰狼优化算法的数学模型中，由称为第1优解、第2优解、第3优解的α,β,δ来锁定目标解向量，剩余解向量称为Ω，并根据前3者所在位置进行移动，最终完成猎物的攻击。狩猎过程的数学表达[16]如下所示：

(1)包围。

包围行为的数学表达如式(6)～式(7)所示：

D=|G·Xp(t)-X(t)|

(6)

X(t+1)=Xp(t)-A·D

(7)

其中，D表示灰狼和猎物的距离;t表示当前迭代次数;A和G表示参数向量，A=2a·r1-a，G=2×r2;向量r1和r2是大小在[0,1]的随机数;Xp表示猎物的位置向量;X表示某个灰狼个体的位置向量;a为收敛因子，其值在每一次迭代中从2到0线性递减。

(2)捕获。

当狼群成功包围猎物后，狩猎通常由α狼带领，β狼和δ狼则跟随并更新位置，辅助α狼追捕猎物。为了从数学模型上模拟这种活动，可以假设α(第1优解)狼、β(第2优解)狼和δ(第3优解)狼均对猎物的潜在位置(全局最优解)有更好的了解，因此整个狼群中每个灰狼个体的位置更新可由式(8)确定：

(8)

X1=Xα-A1·Dα

(9)

X2=Xβ-A2·Dβ

(10)

X3=Xδ-A3·Dδ

(11)

Dα=|G1·Xα-X(t)|

(12)

Dβ=|G2·Xβ-X(t)|

(13)

Dδ=|G3·Xδ-X(t)|

(14)

其中，Xα，Xβ和Xδ为第t次迭代时排列前3的最优候选解,A1，A2和A3表示参数向量,G1，G2和G3也表示参数向量。

在基本灰狼优化算法中，灰狼位置向量的各维取值是连续型的，而在特征选择方法中灰狼取值必须为0或1，所以需要使灰狼的位置二元化[17]。在IGWOSMOTE方法中，各灰狼位置向量的组成是特征子集和SVM参数，长度为二者之和，因此当灰狼改变位置时，则使用式(15)二元化位置：

(15)

其中，Xi,j是指狼群中第i只狼的位置向量的第j维的值。此时灰狼位置向量的二元化设置已完成，可用于特征选择方法中。

3 IGWOSMOTE+SVM分类方法

3.1 IGWOSMOTE方法

首先，基本灰狼算法易受局部与全局寻优性能不均衡的影响，其中参数a呈线性收敛，这并不符合非线性问题中的优化搜索过程。郭振洲等[18]引入了非线性收敛因数策略，降低a前期的衰减水平，则有利于算法发现全局最优解，提高后期衰减水平，此时a能跳出全局并精准找到局部最优解。邢尹等[19]指出GWO搜索性能也受a的衰减程度影响，为了在均衡全局和局部性能的同时加快收敛速度，引入了衰减阶数，本文将引用前者的理论基础，其收敛因子a的计算方法如(16)所示：

(16)

其中,t是当前迭代次数;tmax是最大迭代次数;p是取值在[0,10]的整数衰减阶数;e是自然底数。衰减阶数越大,则a的收敛速度越快。

其次,本文研究的是利用灰狼算法进行SVM参数(即惩罚因子和核函数参数)优化和特征选择，即为SVM不同类别样本分配不同权重和对样本进行降维处理，同时引入随机采样倍率的取值子集生成新样本。获取相应最优参数的问题可以转化成IGWO求解函数最大值的优化问题，其定义如式(17)所示：

max:y=f(X)

s.t.Rmin≤Ri≤Rmax,i=1，2，…，M,

X=(Ci，γi，f1，f2，…，fN，R1，R2，…，RM)

(17)

其中，X为决策向量，即灰狼初始种群的组成形式;N为特征总数;f(·)为适应度函数，即少数类样本的最终预测精度;Rmin和Rmax分别为少数类样本的采样倍率Ri的最小取值和最大取值[20];M为决策空间的维度，即少数类样本的个数。SVM参数组Ci和γi的定义如式(18)和式(19)所示：

Ci=(Cmax-Cmin)×r+Cmin，i=1，2，…，M

(18)

γi=(γmax-γmin)×r+γmin，i=1，2，…，M

(19)

其中，r为[0,1]的随机数;Cmax和Cmin分别表示惩罚权重C的最大值和最小值;γmax和γmin分别表示核函数参数γ的最大值和最小值。特征向量子集的构成为(f1，f2，…，fN)，每一个元素为0或者1，若为0则代表该特征没有被选择，若为1则代表该特征被选择。采样倍率子集[13]由采样倍率上下界之间的随机整数值组成，采样倍率Ri的定义如式(20)所示：

Ri=round(Rmin+(Rmax-Rmin)×

rand(0，1))

(20)

其中，灰狼个体在Ri的最小取值和最大取值之间取随机整数，并由round(·)函数进行四舍五入操作。

3.2 IGWOSMOTE+SVM分类方法具体步骤

IGWO算法把本文所述相关参数作为SVM模型输入并进行一系列的优化训练，输出结果为最优的采样后训练集。

步骤1生成初始灰狼种群，灰狼个体位置由C、γ、fi及Ri组合构成，定义种群规模及最大迭代次数。

步骤2SVM根据灰狼个体位置对训练集进行学习，以分类准确率作为灰狼个体位置的适应度值。

步骤3利用IGWO算法计算适应度值并降序排列，为狼群划分等级。

步骤4更新参数a、A和G，重新计算所有灰狼个体位置。

步骤5判断当前是否达到最大迭代次数，若是则返回IGWO算法的全局最优解，即C、γ、fi及Ri组合，否则跳转至步骤2继续优化。

步骤6将利用最优的C、γ、fi及Ri组合重新采样获得的训练集加载到SVM模型。

3.3 适应度函数设计

IGWO需要根据每次迭代中的各灰狼位置计算对应的适应度值，该函数值是反映IGWO算法中灰狼个体优劣性的重要评价指标，是衔接IGWO算法与本文要解决的具体优化问题的关键步骤。在IGWOSMOTE分类方法中，灰狼个体位置中有多种参数组合参与，其中包括特征向量参数，因此本文采用分类精度和所选特征数来构造适应度函数，如式(21)和式(22)所示：

(21)

(22)

其中，A表示分类精度;N是特征总数;L表示选中特征的数量,L≤N;权重参数α0和β0用来协调A与N缩减，α0∈[0，1]，β0=1-α0;right表示被正确分类的样本数;total表示总样本数。fitness值越大对应的灰狼个体越优秀，在划分灰狼种群的过程中，适应度函数值排列前3的优解(灰狼个体)将在下一次迭代中起到种群位置更新的导向作用。

4 实验与结果分析

4.1 实验环境

本文实验平台是Windows 10操作系统，Intel Core CPU i5-8265U，8 GB RAM；开发环境是Matlab 2016b，LibSVM(3.24)，选用的是径向基核函数。

4.2 数据集准备

为了验证IGWOSMOTE分类方法的有效性，本文基于UCI中6个标准不平衡数据集进行实验分类，表1列出了各数据集的特征字段。

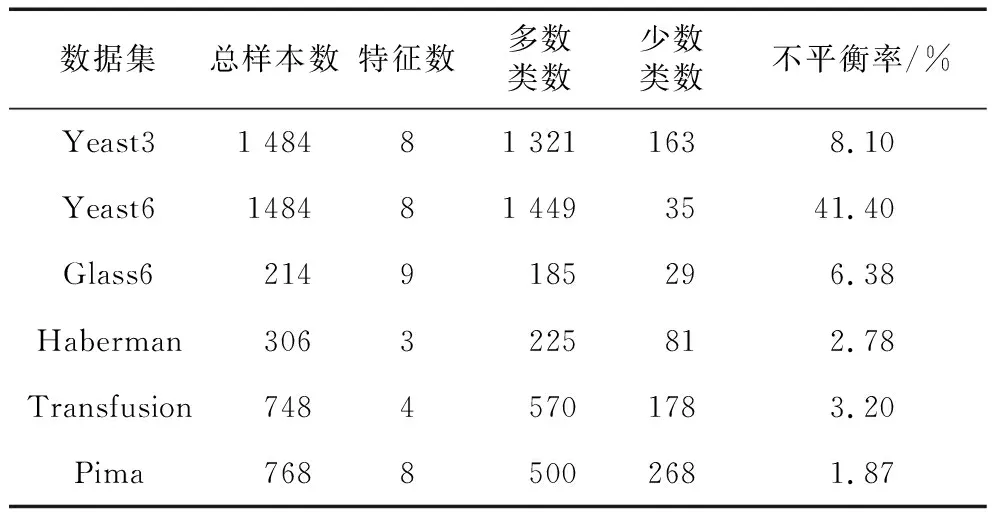
Table 1 Dataset feature fields

4.3 评价方法

传统的SVM模型使用分类准确率[21]作为模型分类结果的评价指标。准确率主要涉及正确分类样本个数和总样本数2个部分，所以更适用于评估平衡数据集。在不平衡数据集的分类结果评估中，可能出现多数类样本的准确率偏高，少数类样本的准确率偏低甚至为0的情况，导致对少数类的分类性能考察不到位。本文采用F_measure[22]和G_mean[23]作为评价指标，两者均需要基于混淆矩阵进行计算，混淆矩阵如表2所示。

Table 2 Confusion matrix

根据表2可得到以下常见的评价指标：

(23)

(24)

(25)

(26)

(27)

查准率(precision)对应于实际正类被正确预测的样本数(TP)与所有被预测为正类的样本数的比值，查全率(recall)对应于正确预测的正类样本数与正确预测的每一类样本数的比值。由式(26)可知，F_measure由precision和recall共同参与评价，且后者两个比值需同时增大才能保证前者指标值也增大，避免了2个比值发生偏向。G_mean是一个几何平均值，根据少数类样本和多数类样本的分类精度计算得到，同样需要2种样本的分类正确率都高才能保证分类器实现公平度量。因此，F_measure可以较好地评价少数类的分类精度，G_mean可以用于评价整体数据集的分类效果。

4.4 实验结果与分析

实现SVM算法并比较SMOTE+SVM方法、GASMOTE+SVM方法和IGWOSMOTE+SVM方法的分类性能。实验基于Matlab平台，实验结果经五折交叉验证获得。初始灰狼种群规模设置为30，C和γ取值上限均为10，下限均为0.001，迭代次数最大设为100。表3和表4分别列出了SVM算法、SMOTE+SVM方法、GASMOTE+SVM方法和IGWOSMOTE+SVM方法在6个数据集上的F_measure和G_mean结果。

表3和表4的实验结果显示，IGWOSMOTE+SVM方法较其他3种方法的少数类分类性能更佳。由F_measure值可以看出，IGWOSMOTE+SVM能有效提高少数类的分类精度，在6个数据集上的预测平均值比SMOTE+SVM提高了6.3个百分点，比GASMOTE+SVM提高了1.27个百分点。由G_mean值可以看出，IGWOSMOTE+SVM分别在Glass6、Haberman、Pima这3个数据集上取得最优的整体分类效果，其平均G_mean值为83.79%，较SMOTE+SVM和GASMOTE+SVM分别增长了2.07个百分点和1.55个百分点。

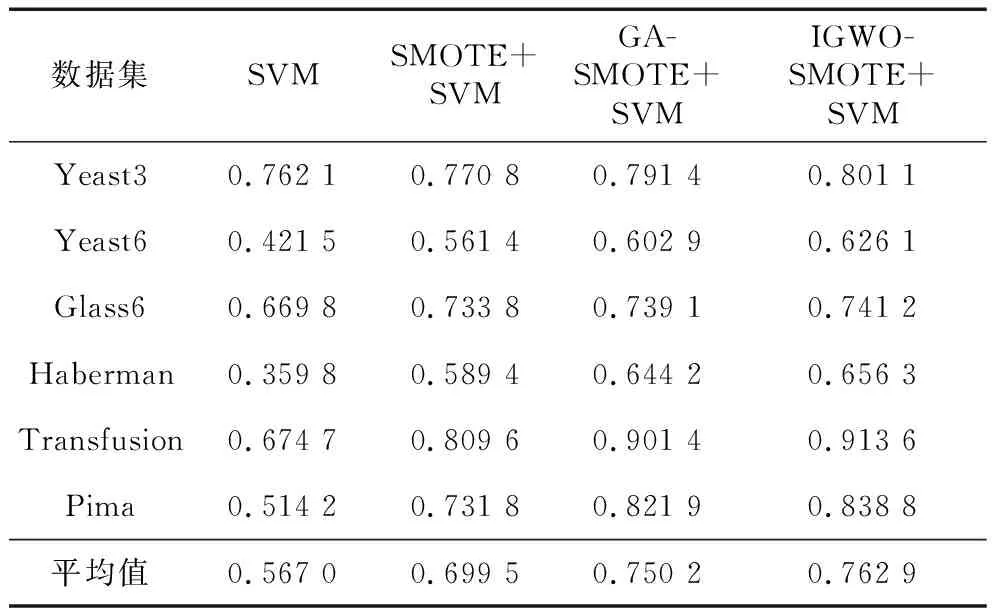
Table 3 F_measure values of

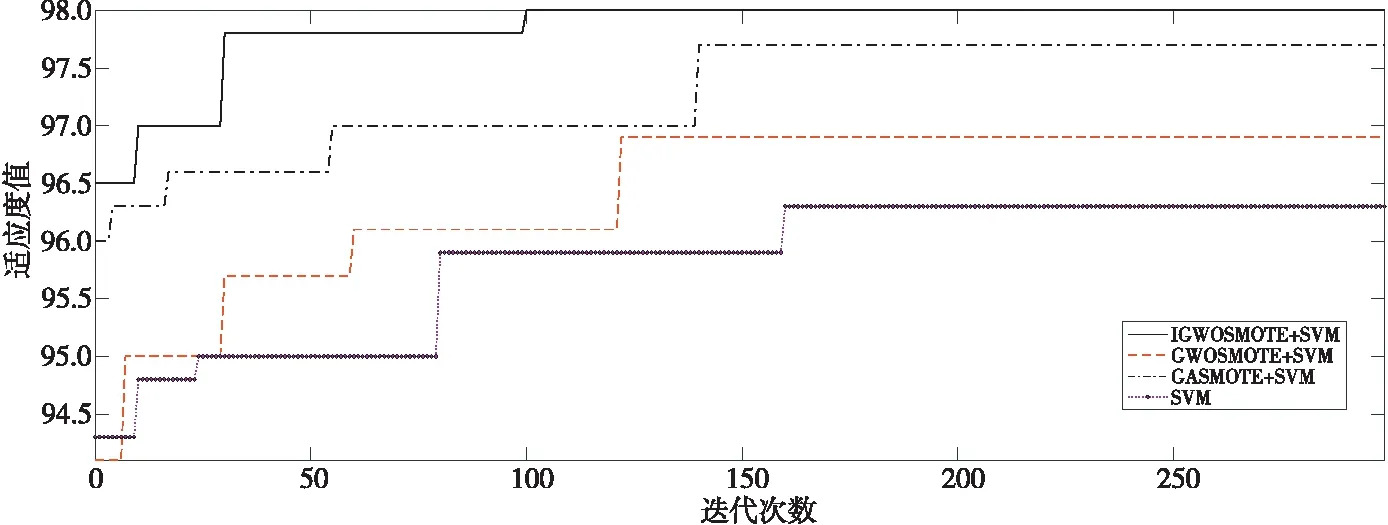
Figure 1 Fitness curves of three methods and SVM algorithm on Yeast3 dataset图1 3种方法和SVM算法在Yeast3数据集上的适应度值曲线

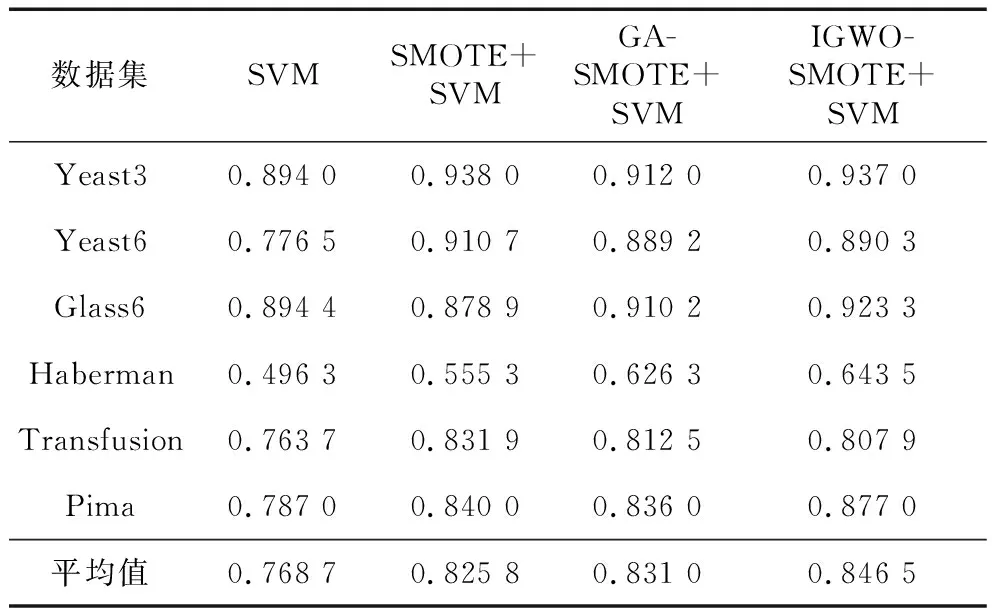
Table 4 G_mean values of different methods based on SVM

IGWOSMOTE+SVM方法采取IGWO自适应搜索策略能获取最优的惩罚参数、核函数参数、特征子集和采样倍率组合，本文根据2种样本的不平衡率对最优惩罚参数进行权重分配，其中以不平衡率为倍率随机增大对少数类的惩罚权重，权重越接近不平衡率，IGWOSMOTE+SVM方法越能达到较优的训练效果。从整体实验数据来看，新方法降低了人为设置采样倍率对分类性能的影响，通过最优特征子集和采样倍率子集对训练集的筛选及重构，可以在一定程度上缓解后期新样本合成之前产生无效样本的现象。另外，灰狼算法自身的局限性可能是导致IGWOSMOTE+SVM方法在其中3个数据集上的G_mean值没有达到最大值的因素。

为了观察和研究IGWOSMOTE+SVM、GASMOTE+SVM、GWOSMOTE+SVM及SVM在6个UCI数据集上的算法优化过程，还在实验过程中绘制了相应的适应度值曲线图，根据6个数据集的优化过程可知，IGWOSMOTE+SVM相较其他方法收敛速度更快，同时也能获得较优的适应度值。由于篇幅限制，本文以Yeast3数据集为例，图1记录了上述3种方法和SVM算法的适应度值迭代过程，从上到下依次为IGWOSMOTE+SVM、GASMOTE+SVM、GWOSMOTE及SVM的适应度值曲线。从图1中可以看出，IGWOSMOTE+SVM的适应度值曲线在第100次迭代后达到完全收敛，最优适应度值为98.09%，通过比较可知，IGWOSMOTE+SVM方法明显具有更快速的收敛速度和最优的适应度值。所以，IGWOSMOTE+SVM方法较其他算法来说更有效，也更有利于在自适应搜索空间中寻得最优解决方案，进而增强最终预测能力。

5 结束语

本文结合灰狼优化算法与SMOTE算法，提出了基于灰狼特征选择和智能设置采样倍率的IGWOSMOTE方法，实验结果表明了IGWOSMOTE+SVM方法的可行性。利用IGWOSMOTE方法训练得到的SVM模型分类器在提高少数类数据的分类精度上有了比较大的改观，且在整体数据集上也获得了较稳定的分类性能，改善了SVM对不平衡本身的敏感度，有利于解决失衡数据的分类问题。然而，对于分类器参数及采样过拟合的问题，IGWOSMOTE方法仍有缩短算法运行时间及提高分类精度的需求，未来将针对灰狼算法易陷入局部最优解、影响过采样方法的问题作进一步研究。