引入启发信息的粒子群算法在低碳TSP中的应用*

申晓宁，潘红丽，陈庆洲，游 璇，黄 遥

(1.南京信息工程大学自动化学院,江苏 南京 210044；2.江苏省大气环境与装备技术协同创新中心,江苏 南京 210044；3.江苏省大数据分析技术重点实验室，江苏 南京 210044)

1 引言

众所周知，二氧化碳(CO2)是引起温室效应的主要因素，美国国家海洋和大气局NOAA(National Oceanic and Atmospheric Administration)称，在所有造成全球变暖的温室气体中，CO2占63%。根据国际能源署IEA(International Energy Agency)的数据，2019年全球碳排放量的增长约为330亿吨。除了发电供热，全球第二大二氧化碳排放量贡献者便是交通运输，交通运输产生的二氧化碳占全球二氧化碳排放量的23%，而交通运输总碳排放量的主要来源是道路运输[1]。因此，对于车辆路径的优化不仅要考虑耗时最少和路径最短，同时也要考虑低碳环保这一要素。

旅行商问题TSP(Traveling Salesman Problem)[2]可以被看作车辆路径问题VRP(Vehicle Routing Problem)的特例，即单一车辆的VRP。TSP的应用极其广泛，VRP[3]、机器人路径规划[4]等工程问题都可以转化成TSP进行求解。文献[3]将TSP的解进行拆分并将其转化为VRP的解。文献[5]使用启发式算法求解VRP，为每辆车分配客户点并通过求解TSP确定该车的最优路径。此外，TSP还可以作为并行机器调度问题中的一个排序子问题[6]。目前，关于TSP的研究大多将总的行驶距离最短作为优化目标。然而，随着环境状况每日愈下，污染物排放和燃料消耗所造成的环境治理成本越来越高，人们在交通运输领域也开始考虑“绿色物流”的践行。国家在“十四五规划纲要”中也提出了广泛形成绿色生产生活方式的要求和碳排放总量持续减少，生态环境持续改善的目标。为响应这一号召，近年来，一些学者将TSP与环境问题相结合，以降低能源消耗，减少CO2排放，缓解温室效应为优化目标。Wang等[1]研究了能耗最小化的TSP，采用改进的分支定界方法最小化车辆的载重与行驶距离的乘积，但该方法仅在小规模问题中能够获得最优解。Kaabachi等[7]研究了一类带时间窗的绿色TSP，将蚁群算法与局部搜索相结合，确定车辆速度从而将燃油消耗降至最低。文献[8]建立了一个最小化碳排放量的TSP模型，考虑了载重对碳排放的影响，并采用改进的蛙跳算法进行求解。然而，上述方法都存在着群体多样性丧失快、求解精度低和问题启发信息利用少等缺点。为了改善这一现象，本文在低碳TSP现有工作的基础上，建立符合实际的低碳旅行商问题LCTSP(Low-Carbon Traveling Salesman Problem)的数学模型，并考虑在群智能算法中设计一系列问题特征驱动的改进策略，以提高算法的多样性和求解精度。

群智能优化算法是能够有效求解NP-hard问题[9]的一类算法，Kennedy等[10]于1995年提出的粒子群算法PSO(Particle Swarm Optimization)便是其中的典型代表。它通过初始化、适应度评价、速度和位置更新等阶段产生较优后代，实现进化迭代。与其余群智能算法相比，PSO还依靠粒子速度完成搜索，并且在迭代进化中只有最优粒子把信息传递给其他粒子，搜索速度更快。此外，PSO还具有记忆性、自我学习能力和社会学习能力，搜索精度也更高。大量学者对PSO算法的改进及其应用做了深入研究。Xia等[11]提出了一种三重档案粒子群算法，该算法通过选择合适的学习样本建立粒子学习模型。文献[12]提出一种自适应多策略行为粒子群优化算法，为群体中的每个粒子提供多种行为进化策略。Marinakis等[13]采用包含3种自适应策略的多自适应粒子群优化算法求解带时间窗的车辆路径问题。文献[14]提出Beam-PSO优化算法，解决了一类多行程车辆路径问题。因此，本文选择PSO算法作为所提模型的基本求解算法，结合问题的启发信息，提出一种基于启发信息的离散粒子群算法HDPSO(Heuristic Discrete Particle Swarm Optimization)。实验结果表明，所提算法具有更高的求解精度。

2 低碳旅行商问题

2.1 低碳旅行商问题的模型

与传统TSP不同，LCTSP的优化目标是确定车辆在运输过程中碳排放量最小的路线。由于运输过程中载重量不断变化，车辆行驶相同的距离，碳排放量可能是不同的。因此，LCTSP模型有着更强的实用性，更满足 “节能减排”的理念。假设LCTSP共有n个节点(包括仓库和客户点)，货车在运输过程中以匀速运动且燃烧效率不变，建立LCTSP的数学模型如式(1)～式(6)所示：

(1)

(2)

s.t.Xij=1 or 0,i≠j

(3)

(4)

(5)

(6)

其中，式(1)表示LCTSP的目标，即最小化一次运货过程中所有节点之间路径段的碳排放量之和，第i、j个节点间路径段的碳排放量为节点间的直接距离dij与对应距离的碳排放量系数ε(Mij)的乘积；式(2)给出ε(Mij)与节点间的载重量Mij的函数关系[9]；式(3)～式(6)为模型的约束条件，其中式(3)～式(5)保证货车能经过所有节点且每个节点仅经过一次，Xij表示货车是否选择节点i和节点j之间的路径，Xij=1表示选择，Xij=0表示未选择；式(6)防止货车超载，保证各客户节点总的需求量不超过载重量，mi(i=2,3,…,n)表示除仓库点之外每个节点的需求量，M1表示货车从仓库出发时的载重量，M0表示货车的最大载重量限制。

2.2 模型有效性的验证

为了验证模型的正确性和有效性，即LCTSP模型能够在对车辆行驶距离影响较小的情况下大幅度减少碳排放量，本节分别实验了以最短行驶距离为目标的经典TSP和以最小碳排放为目标的LCTSP。在公开数据集TSPLIB[15]中10个不同规模实例的基础上，随机生成载重和各客户节点的需求量信息。2种模型的对比结果如表1所示(实例名称中的数字表示TSP的规模)。其中，经典TSP中的最短行驶距离在TSPLIB中是已知的，碳排放量则是将最短行驶距离对应的最优路径代入2.1节LCTSP模型中的目标(即式(1)和式(2))计算得出的；LCTSP中的碳排放量是采用本文3.1节提出的HDPSO算法求解LCTSP数学模型得出的最优碳排放量值，再通过其对应的最优路径求出行驶距离。表中还给出了与经典TSP相比，LCTSP行驶距离或碳排放量的增加或减少百分比，“↑”表示增加，“↓”表示减少。

从表1中可以看出，与经典TSP相比，虽然LCTSP模型在总的行驶距离上有所增加，但在10个实例中，有6个增加的百分比都小于1%，其余4个实例增加的百分比也均小于7%，这表示该模型对行驶距离的影响总体很小。在碳排放量方面，LCTSP模型相比经典TSP减少的幅度很大。例如，在实例gr14和fri26上，它们的运输距离之差为0，但是碳排放量却分别减少了17.65%和12.65%；在大规模实例pr152上，虽然运输距离增加了6.70%，但是碳排放量却减少了11.21%。这些数据表明，LCTSP模型正确且有效，它以低碳作为性能指标，能够在保持车辆行驶距离较短的同时大幅度减少碳排放量，实现了“绿色运输”。

Table 1 Results comparison of classic TSP and LCTSP

3 求解LCTSP的HDPSO算法

针对所建LCTSP模型，本文提出一种基于启发信息的离散粒子群算法HDPSO。本节给出HDPSO的算法框架，并详细介绍采用的新型离散个体生成算子和改进策略。

3.1 HDPSO算法框架

HDPSO算法求解LCTSP模型的框架如图1所示。HDPSO主要由4个模块组成:(1)初始化;(2)种群中新个体的生成;(3)个体极值和全局极值的更新;(4)个体极值和全局极值的局部搜索。具体实现步骤如算法1所示。

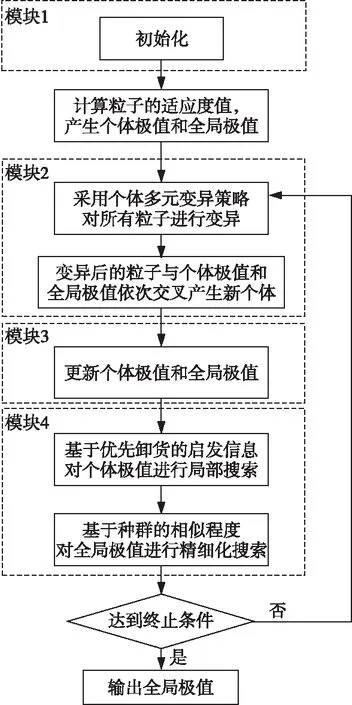
Figure 1 The framework of HDPSO to solve LCTSP 图1 HDPSO求解LCTSP的框架图

算法1基于启发信息的离散粒子群算法

Input:N(种群规模)、n(城市规模)、Y(邻域数量)、Pr(逆转变异选择概率)、α(优先卸货城市点比例)、K(相似度阈值)。

Output:Xg(最优个体)。

01:随机生成N个体Xi(i=1,2,…,N) ，计算每个个体的适应度fitness(Xi);

02:确定种群的全局极值Xg和每个个体的个体极值Xip;

03:Whiletermination criterion not fulfilleddo

04:fori=1 toNdo

05:Xi←m_Mutate(Xi,Pr);/*个体多元变异(交换、逆转、插入)*/

06:Xinew←Greedy_Crossover(Xi,Xip);/*个体与个体极值贪婪交叉生成新个体Xinew*/

07:iffitness(Xinew) ≤fitness(Xi)

08:Xi=Xinew;

09:Xinew←Greedy_Crossover(Xi,Xg);/*个体与全局极值贪婪交叉生成新个体Xinew*/

10:iffitness(Xinew)≤fitness(Xi)

11:Xi=Xinew;

12:iffitness(Xi)≤fitness(Xip)

13:Xip=Xi;//更新个体极值

14:iffitness(Xi)≤fitness(Xg)

15:Xg=Xi;//更新全局极值

16:Xip←p_unload(Xip,α);/*基于优先卸货启发信息对个体极值进行局部搜索*/

17:Xip(round(α*n)+1:n) ←Reversion(Xip(round(α*n)+1:n));/*未卸货的剩余位进行逆转变异*/

18:endfor

19:Xg←Gbest_Search(X,Xg,Y,K,N);/*基于种群相似度对全局极值进行精细化搜索,X表示个体集合*/

20:endwhile

21:OutputXg

3.2 新型离散个体生成算子

标准PSO算法是针对连续优化问题设计的，粒子的速度和位置更新如式(7)和式(8)所示：

(7)

(8)

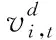
3.2.1 保持“惯性”的个体多元变异策略

个体多元变异策略实现方法的伪代码如下所示：

m_Mutate(X,Pr)

Input:逆转变异的概率Pr、个体X。

Output:变异后的新个体Xnew。

01:Ps=Pi=(1-Pr)/2;

02:index←Roulette(Ps,Pr,Pi);/*基于轮盘赌选择变异方式的序号*/

03:ifindex==1

04:Xnew←Swap(X)；//交换变异

05:elseifindex==2

06:Xnew←Reversion(X)；//逆转变异

07:elseifindex==3

08:Xnew←Insertion(X)；//插入变异

09：OutputXnew

首先，根据输入的逆转变异概率Pr计算交换变异和插入变异的概率Ps和Pi(第1行);接着，基于轮盘赌选择变异方式的序号(第2行);若为方式1，则对个体进行交换变异(第3～4行);若为方式2，则对个体进行逆转变异(第5～6行);若为方式3，则对个体进行插入变异(第7～8行)。最后输出变异后的新个体。

3.2.2 跟踪极值的贪婪交叉算子

为了引导个体朝着最优解的方向移动，本文根据LCTSP的特征设计了一种跟踪极值的贪婪交叉算子。首先，交叉是两个离散个体之间的信息交互，因此它可以用于个体与个体极值以及个体与全局极值之间的信息交流。其次，将载重与距离信息同时引入算子中，保证个体的“贪婪性”,即个体顺序访问的城市都是碳排放量相对较少的城市，该算子的设计不仅使得PSO适用于求解LCTSP这类离散问题，同时也提升了算法的收敛速度。

贪婪交叉的实现伪代码如下所示：

Greedy _Crossover (Xpbest,X)

Input:个体极值Xpbest、个体X。

Output:新个体Xnew。

01:Xnew←0;

02:选择仓库点作为起始城市S;

03:将S加入Xnew并从Xpbest和X中删除S;

04:从Xpbest和X中选择城市S的左右相邻城市作为候选城市{SLp,SRp,SLX,SRX};

05:从 {SLp,SRp,SLX,SRX}选择城市S′，使得S′和S之间的路径碳排放量最小；

06:将S′加入Xnew并从Xpbest和X中删除S′;

07:whileXis not emptydo

08:ifS′∈{SLp,SLX}

09: 将S′设为下一个出发城市S;

10: 在S的左候选城市{SLp,SLX}中选择新的S′作为下一个访问的城市，使得S′与S之间的路径碳排放量最小;

11:else

12: 将S′设为下一个出发城市S;

13: 从S的右候选城市{SRp,SRX}中选择新的S′作为下一个访问的城市，使得S′与S之间的路径碳排放量最小;

14:endif;

15: 将 S′加入Xnew并从Xpbest和X中删除S;

16:endwhile

17:OutputXnew

该算子以个体与个体极值进行交互为例，个体与全局极值的交互同理。

首先以仓库点作为新个体的出发城市S(第2～3行)。从城市S的左右相邻城市{SLp,SRp,SLX,SRX}中选择城市S′,使得城市S′与城市S构成碳排放量最少的路径段(第4～6行)。第8行区分了两种情况:一是下一个访问的城市S′属于城市S的左侧相邻城市集合，此时由于从个体极值Xpbest和个体X中删除了S，城市S′右侧相邻城市为空，将S′设为下一个出发城市S，从S的左候选城市{SLp,SLX}中选择新的S′作为下一个访问的城市(第8～10行);二是S′是从城市S的右侧相邻城市集合中选择的，此时，城市S′左侧城市为空，将S′设为下一个出发城市S，从S的右候选城市相邻城市集合{SRp,SRX}中选择新的S′作为下一个访问的城市(第11～13行)。为了避免重复访问某些城市，只从当前未选择城市中选择下一个访问的城市。第8～14行重复执行，直到访问了所有城市并生成了新的个体。

3.3 考虑优先卸货的个体极值局部搜索策略

由式(7)可知，个体极值和全局极值是参与信息交互的主要信息源，随着迭代的进行，种群越来越相似，跳出局部最优解的能力也越来越弱，最终将导致算法搜索停滞，而局部搜索是一种跳出局部最优的有效方法。基于上述分析并结合问题的启发信息，本文提出考虑优先卸货的个体极值局部搜索PU_PLS(Priority-Unloading Personal best Local Search)策略。从个体极值的前α*n位中依次贪婪选取相距最近的城市，避免在行驶初期因为载重过大造成大量的CO2排放。此外，对个体极值中剩下的(1-α)*n位进行逆转变异，以增加搜索的多样性，有效地避免种群陷入局部最优。

PU_PLS的实现方法如图2所示。假设①点为车辆的出发点。首先，从①点出发，依次选择距离前一点最近的城市优先卸货，直至确定好前α*n个节点，并用它们替代原个体极值的前α*n位。接着，确定当前个体极值回路中的缺少城市和重复城市，并用缺少城市依次替代重复城市。最后，为了防止算法过度贪婪，在剩下的(1-α)*n位中随机产生2个变异点，并在这两点之间进行逆转变异，产生新的个体极值。

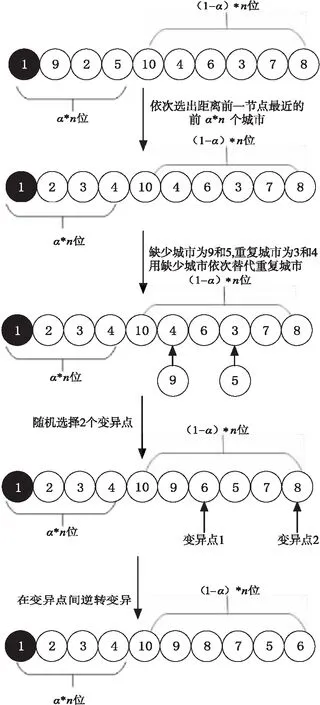
Figure 2 Schematic diagram of personal best local search operation considering priority unloading图2 考虑优先卸货的个体极值局部搜索过程示意图

3.4 考虑同化程度的全局极值精细化搜索策略

在粒子群优化算法中，每一个新个体的生成都需要与全局极值进行信息交互，因此，全局极值的优劣很大程度上决定了个体的搜索质量，也主导了种群的走向。针对这一现象，本文提出考虑同化程度的全局极值精细化搜索ASS_GRS(ASSimilation Global best Refined Search)策略,采用2-Opt算子对全局极值进行局部搜索，判断种群与全局极值的相似程度，当种群的相似度高于阈值时，表示该种群已被同化，此时选择点插法对个体极值进一步挖掘，以改变个体交互的信息源。该策略根据种群相似度及时调整信息交互源，不仅提高了搜索精度，也降低了种群的同化速度。

ASS_GS的实现伪代码如下所示:

Gbest_Search(X,Xgbest,Y,K,N)

Input:个体X，全局极值Xgbest，邻域解数量Y,相似度阈值K，种群规模N。

Output:全局极值Xgbest。

01:Xgbest←2_opt(Xgbest,Y);/*利用2-Opt对全局极值进行优化*/

02:forq=1 toNdo

03：smq←similar(Xq,Xgbest);/*计算群体中的个体与全局极值之间的相似度*/

04:ifminq(smq)>K

05:Xgbest←Dot_Insertion(Xgbest);/*点插法优化全局极值*/

06:OutputXgbest

首先，将2-Opt算子[17]作用在全局极值上(第1行)。接着判断种群中每个个体与全局极值的相似度。假设种群中第q个个体与全局极值的相似度为smq，将其定义为第q个个体和全局极值取值相同的位数与总位数之比，如式(9)所示：

q=1,2,…,N；i=1,2,…,n

(9)

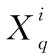
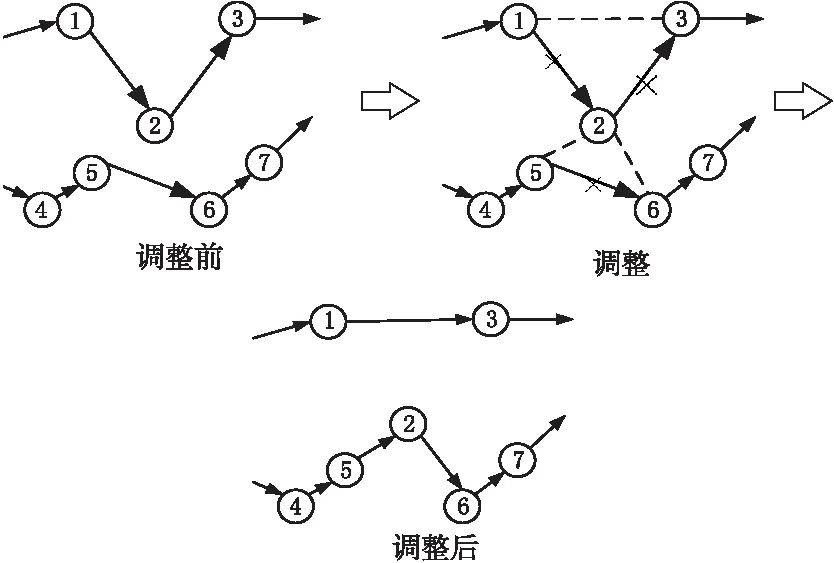
Figure 3 Diagram of point-interpolation图3 点插法过程示意图

3.5 复杂度分析

对HDPSO算法的时间复杂度分析如下：初始种群个体极值和全局极值的确定为O(Nn)，新个体生成为O(Nn)，个体极值和全局极值的更新为O(N)，考虑优先卸货的个体极值局部搜索为O(Nn)，考虑同化程度的全局极值精细化搜索为O(Nn)。综上,HDPSO算法总的时间复杂度为上述结果中的最大值O(Nn)。对HDPSO算法的空间复杂度分析如下：种群初始化时产生N个n维的个体,其空间复杂度为O(Nn)，因为算法中个体更新都在原有个体上替换，不需要占用新的运算空间，所以算法的空间复杂度为O(Nn)。相较于基本PSO算法的时间复杂度O(Nn)和空间复杂度O(Nn)，本文所提HDPSO算法的计算复杂度未增加。

4 实验仿真与结果分析

为了验证所提HDPSO算法和改进策略的有效性，本节采用Matlab R2017b软件进行仿真实验，计算机处理器参数为Intel(R) Core(TM) i5-5500U CPU@ 2.40 GHz，8 GB运行内存。设计3组实验：(1)针对所提策略中引入的新参数，选取不同的数值进行实验对比，确定最优的参数取值；(2)改进策略的有效性验证；(3)将所提HDPSO算法与文献中6种代表性算法进行对比，以验证所提算法的性能。本节所有实验采用与2.2节相同的10个LCTSP实例。

4.1 参数分析

HDPSO算法中的粒子群规模N和邻域解数量Y分别是标准PSO和2-Opt算子中的常用参数。本文实验取文献中的常用值N=200,Y=10[17,19]。而逆转变异选择概率Pr、优先卸货城市点比例α和相似度阈值K为新引入的参数，需要对这3个参数进行取值分析。由于它们的取值均在[0,1]，因此以0.1为间隔在[0,1]上选取不同的参数值，对HDPSO算法的求解精度进行对比。在依次分析每个新引入参数时，固定粒子群算法自身参数(例如粒子群规模等)的取值不变。为减少随机性影响，算法在每一参数取值下分别运行30次。以规模为51的测试实例eil51为例，实验结果如表2所示。其中，Best表示30次运行搜索到的最佳碳排放量，Avg表示30次运行求得的平均碳排放量,Best和Avg的最佳值均加粗表示。

由表2可知，对于逆转变异选择概率Pr，当Pr等于0或1时，HDPSO的求解结果最差;当Pr=0时，表明此时算法中不存在逆转变异，而逆转变异是相对其他2种变异方式更加具有问题特征启发性的变异方式;当Pr=1时，表明此时算法中只存在逆转变异，而无其他2种变异方式，从而缩小了个体的搜索范围，导致种群多样性的流失;当Pr∈[0.4,0.8]时,最优解Best的值是相同的，均值Avg在Pr=0.6时最小，此时算法更加稳定。对于优先卸货城市点比例α，当α=0时，算法未采用考虑优先卸货的个体极值局部搜索策略，求解精度较差；当α=1时，由于过度贪婪，种群极易陷入局部最优。考虑卸货具有依次选取最近城市这一规则，α越高，则种群中的个体越相似。基于上述分析，α应取大于0的较小值，从实验结果上也得到了：当α∈[0.2,0.4]时，HDPSO搜索到的最优解Best最好，且在α=0.2时均值Avg最小。对于相似度阈值K，极端的取值会使算法的求解能力变得很差:当K=0时，表示每一次迭代都需要对全局极值进行点插法优化，增加了种群的同化概率；当K=1时，表示种群的相似度一直不会满足阈值条件，此时，考查群体同化程度的机制和点插法策略均将失效。由表2可知，当K∈[0.6,0.8]时，HDPSO求得的Best最好，且在K=0.6时的均值Avg最小。综上，对所提算法HDPSO引入的3个新参数的最佳取值如下：Pr=0.6,α=0.2,K=0.6。后文实验均采用这组参数值，以最大目标评价次数MAXFE为100 000作为算法的终止条件。

Table 2 Results comparison with different parameters on the eil51 example

4.2 改进策略的有效性验证

4.2.1 新型离散个体生成算子的有效性验证

为检验3.2节设计的新型离散个体生成算子NDO的有效性，将HDPSO算法中的算子NDO分别替换为现有文献中基于随机交换序列的个体生成算子RES(Random Exchange Sequence)[20]和基于部分映射交叉的个体生成算子PMX(Partially Mapped cross)[21]，将由此得到的2种算法与HDPSO进行对比。每种算法仍是独立运行30次。表3统计了3种算法在10个规模不同实例上的最优值(Best)和平均值(Avg)。为显著对比3种算子的优劣，本文引入显著水平为0.05的Wilcoxon秩和检验对30次实验结果进行统计测试，其中，“+”表示NDO显著优于对比算子，“=”表示两者无明显差异，“-”表示NDO显著劣于对比算子。

表3选择了10个规模递增的LCTSP实例测试3种算子的有效性。可以看出，随着问题规模的增大，RES和PMX的寻优能力明显不能满足求解精度的需要，搜索到的路径解具有较大的碳排放量，但NDO仍具有较好的表现：与RES和PMX相比，NDO分别在9个(除小规模实例gr24以外)和8个实例(除小规模实例gr24和fri26以外)上获得了更优的最优值Best，在全部10个实例上取得了最佳的平均值Avg。同时，统计测试结果显示，在所有实例上，NDO均显著优于RES和PMX。原因主要在于NDO将低碳旅行商问题的启发信息与PSO算法的结构相融合，使个体多元变异保留了标准PSO中的“惯性”，同时贪婪交叉实现了个体与个体极值和全局极值之间信息的交互。个体多元变异有利于维护群体的多样性，而利用贪婪思想尽可能提取个体、个体极值和全局极值中的有效信息，保证了算法的求解精度和收敛速度。但是，贪婪思想易导致算法陷入局部最优，出现早熟收敛，因此也需要配合其他一些改进策略进一步提升算法性能。

Table 3 Statistics of solving results of three discrete individual generating operators

4.2.2 2种改进策略的有效性验证

为了验证2.3节考虑优先卸货的个体极值局部搜索策略PU_PLS和3.4节考虑同化程度的全局极值精细化搜索策略ASS_GS的有效性，在HDPSO算法中分别删除其中一种策略，产生2种只有单一策略的算法(HDPSO-PU_PLS和HDPSO-ASS_GS)。将它们与HDPSO进行对比，以分析每种改进策略对HDPSO性能的影响。实验结果如表4所示。

由表4可知，综合运用了2种改进策略的HDPSO算法在求解精度上有了大幅度提升。HDPSO-PU_PLS和HDPSO-ASS_GS分别在前3个和前5个中小规模实例上与HDPSO算法的最优值Best一致，在剩余的中大规模实例上搜索到的Best值均劣于HDPSO算法。对于平均值Avg，删除单一策略后的2种算法在所有10个实例上均劣于HDPSO算法。同时，统计测试结果表明，在绝大多数实例上，HDPSO算法删除单一策略后会导致求解性能显著变差。究其原因，首先，策略PU_PLS引入了LCTSP问题的启发信息对个体极值进行局部搜索，这有利于增强算法对解空间的探索能力;其次，策略ASS_GS考虑种群相似度，对全局极值进行精细化搜索，保证了信息交互的质量，提升了个体的求解精度；最后，基于种群相似度及时调整交互信息源的思想也有助于降低种群同化速度。总之，上述实验结果验证了所提改进策略存在的必要性和有效性。

Table 4 Results comparison between HDPSO algorithms and algorithms those single strategy

4.3 HDPSO算法的性能验证

为验证HDPSO算法在求解LCTSP时的性能，将HDPSO算法与现有算法进行对比。由于目前文献中几乎没有直接求解LCTSP的算法，因此，实验复现了6种具有代表性的求解TSP的算法，将它们分别应用于本文建立的LCTSP模型，并与HDPSO算法进行对比。

4.3.1 与经典算法的对比

选取3种经典搜索算法(模拟退火SA(Simulated Annealing)法[22]、禁忌搜索TS(Tabu Search)算法[23]和遗传GA(Genetic Algorithm)算法[24]与HDPSO算法进行对比。算法的参数设置如表5所示，每种算法运行30次，实验结果如表6所示。

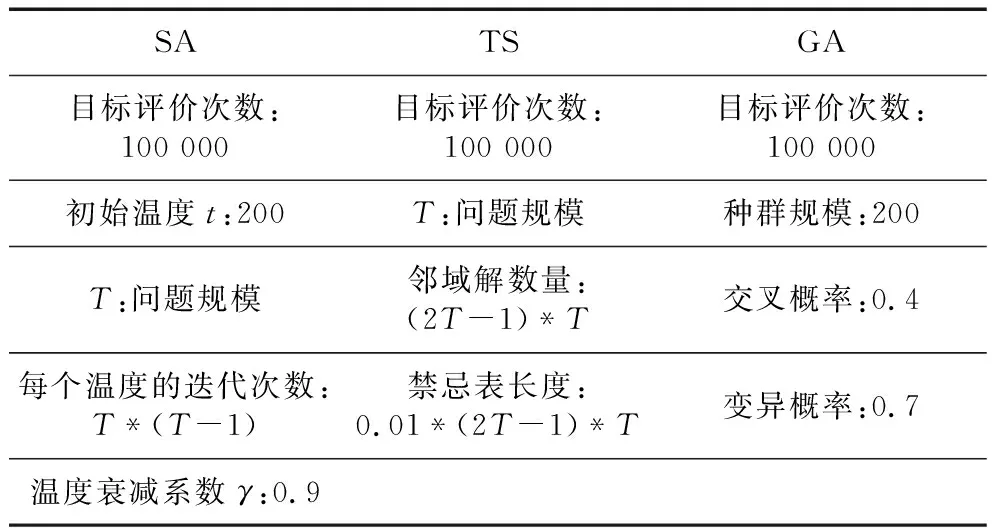
Table 5 Parameters setting of SA,TS and GA

由表6可见，在小规模实例gr24，fri26和bays29上，SA,TS,GA和HDPSO的最优值Best一致;在其余7个实例上，HDPSO能获得更优的Best。对于所有实例,HDPSO的平均值Avg都优于SA和TS的，仅在gr24上的平均值与GA的相同。通过显著水平为0.05的Wilcoxon秩和检验可以发现，HDPSO在所有实例上的求解结果均显著优于SA和TS的；与GA相比，HDPSO仅在小规模实例pr24和fri26上的结果与GA的无显著差异，而在其它所有实例上均显著更优。综上，相较于SA,TS和GA，HDPSO表现出了更高的求解精度。

Table 6 Experimental results comparison of HDPSO,SA,TS and GA

4.3.2 与新型代表性算法的对比

为了进一步验证所提算法的性能，从近期文献中选择了基于粒子群算法+蚁群算法+3-Opt算法的混合算法PSO+ACO+3-Opt[19]、蜘蛛猴DSMO(Discrete Spider MOnkey)算法[2]和改进遗传算法IGA(Improved Genetic Algorithm)[25]与HDPSO算法进行对比。算法的参数设置如表7所示，每种算法运行30次，实验结果如表8所示。

Table 7 Parameters setting of comparative algorithms

由表8可见，与其它3种新型算法相比，本文HDPSO算法在绝大多数实例(尤其是中大规模实例)上取得了最佳的最优值Best和平均值Avg。显著水平为0.05的Wilcoxon秩和检验结果表明，HDPSO分别在9个、10个和7个实例上显著优于PSO+ACO+3-Opt,DSMO和IGA，而仅在实例att48上显著劣于IGA。

Table 8 Results comparison between HDPSO and algorithms from recent literatures

上述各组实验结果表明，本文HDPSO算法对于不同规模的LCTSP的综合性能优于各类对比算法。主要原因有：HDPSO算法融入了问题特定的启发信息，使得个体向最优解的移动更有针对性;新型离散个体生成算子提升了算法的求解精度，加快了算法的收敛速度;考虑优先卸货的个体极值局部搜索策略对个体极值进行局部搜索，在防止算法早熟收敛的同时增强了对解空间的探索能力；全局极值精细化搜索策略基于种群相似度及时调整信息交互源，降低了种群同化速度，保证了信息交互的质量。综上，本文HDPSO算法的求解精度高且稳定性好。

5 结束语

针对当前碳排放污染日益严峻的社会现象，本文研究了低碳旅行商问题LCTSP。所做工作和结论如下：(1)建立LCTSP的数学模型，并验证了模型的有效性。(2)针对LCTSP的特点，设计了一种新型离散个体生成算子，对个体自身采用多元变异策略，保持个体的“惯性”，同时采用贪婪交叉策略实现个体与个体极值和全局极值之间信息的交互。同时，为了解决由于个体生成的贪婪性导致的种群早熟收敛问题，提出考虑优先卸货的个体极值局部搜索策略和考虑种群同化程度的全局极值精细化搜索策略。实验结果表明，本文所提2种策略与个体生成算子的结合极大地提升了算法的求解精度，删除任意一种策略都会显著降低HDPSO的性能。(3)将本文算法与文献中6种具有代表性的算法进行对比，实验结果表明，HDPSO算法在求解精度和稳定性方面优于所有对比算法，能在绝大多数不同规模的问题中搜索到碳排放量最小的全局最优路径。