复杂环境下基于自适应深度神经网络的鲁棒语音识别*

张开生,赵小芬

(陕西科技大学电气与控制工程学院，陕西 西安 710021)

1 引言

随着人工智能的迅速发展，语音识别技术作为人机接口的关键技术，受到国内外学者的广泛关注[1 - 4]。近年来，深度神经网络DNN(Deep Neural Network)因其强大的建模能力逐渐发展为语音识别领域的主流模型[5]。相比于传统的高斯混合-隐马尔科夫模型GMM-HMM(Gaussian Mixture Model-Hidden Markov Model)[6]，DNN在语音识别任务中具有显著的优势。然而，在连续语音识别系统中，由于说话人及环境噪声具有多变性，造成训练数据与测试数据之间的不匹配，导致语音识别效果往往难以令人满意[7]。针对这个问题，自适应技术应运而生，它被证明能有效减少说话人差异及环境变化带来的影响[8]。目前，主流自适应技术主要分为基于最大后验概率MAP(Maxumum A Posteriori)准则的自适应方法、基于最大似然回归MLLR(Maximum Likelihood Linear Regression)和基于说话人聚类的方法[9]。其中，基于MAP的说话人自适应通常是假设说话人相关SD(Speaker Dependent)模型的参数服从某种假定的先验分布。基于MLLR自适应方法，通常是在最大似然准则下，利用经过变换后的说话人无关SI(Speaker Independent)模型得到SD模型，虽然这种自适应方式所需数据量相对较少，但是渐进性能较差。基于本征音自适应方法是说话人聚类的典型方法，该方法通过模型参数进行主分量分析PCA(Principal Component Analysis)得到SD模型参数的一组基，在自适应阶段对得到的新的SD模型参数进行限制，从而达到说话人自适应的目的。

针对上述说话人识别自适应技术，相关学者进行了大量的研究，屈丹等[10]将本征音子说话人空间说话人自适应算法用于克服自适应数据量不足时引起的过拟合现象，使用高斯混合模型对本征音子说话人进行建模，在数据量极少的情况下，在一定程度上克服了过拟合的现象，提升了语音识别率。2018年，金超等[11]将i-vector向量作为说话人辅助信息融入DNN声学模型中，在特征空间中进行说话人自适应，将系统单词错误率降低了7.7%。2019年，娄英丹等[12]将MAP和MLLR 2种自适应技术相结合，并将结合后的自适应技术应用于远场噪声混响条件下的语音识别，在一定程度上降低了词错误率。

结合上述语音识别自适应技术的思路及优缺点，本文提出一种新的基于自适应神经网络的语音识别算法，改进自适应准则及特征空间，将说话人身份信息i-vector向量及噪声感知融入系统模型，并将其应用到复杂环境下的语音识别，消除说话人特征的差异性及环境噪声变化的影响，通过提高模型训练数据集及测试数据集间的匹配度，进一步提升语音识别率。

2 基于DNN的声学模型建立

深度神经网络其本质上是一个具有多个隐藏层的多层感知器MLP(MultiLayer Perceptron)，包含输入层、隐藏层和输出层[13]。图1所示为一个5层结构DNN，最开始的一层为输入层，记为第0层，输出层记为第L层。在第L层中，有:

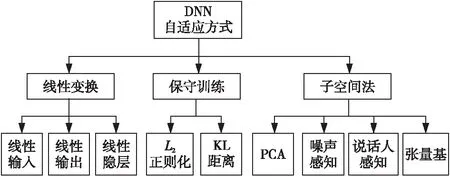
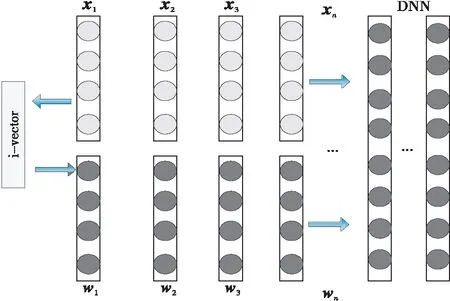
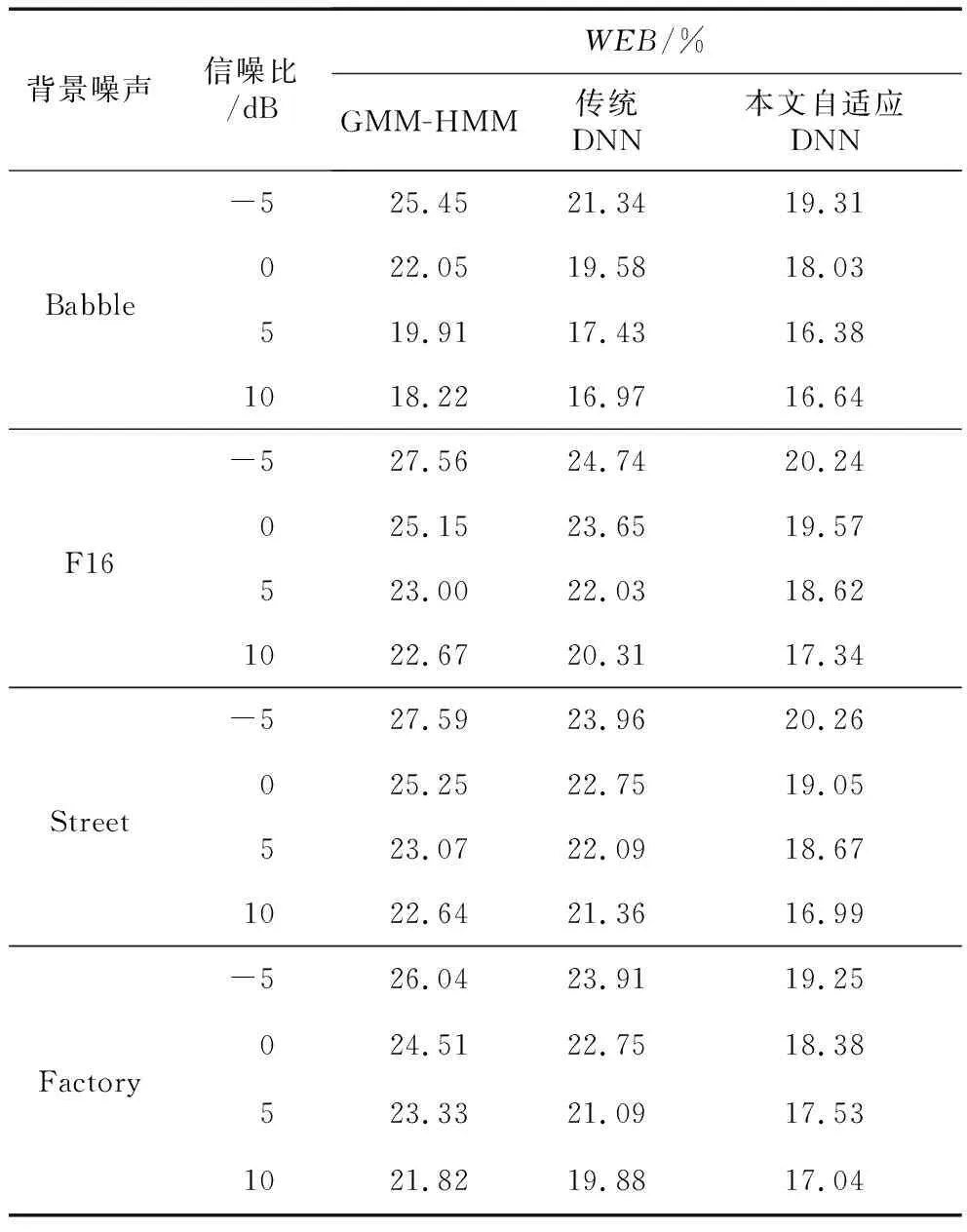
αl=f(Wlαl-1+βl),0

(1)

其中,αl∈RNl×1，Wl∈RNl×Nl-1，βl∈RNl×1，Nl∈R分别为激活向量、权重矩阵、偏差系数矩阵和一层神经元的个数。f(·)为对激励向量进行计算的激活函数，一般选用Sigmoid函数，其表达式如式(2)所示:

(2)

tanh函数为Sigmoid函数的调节版本，二者建模能力相当，其表达式如式(3)所示：

(3)

Figure 1 Typical DNN structure 图1 典型DNN结构

另外,还可以采用Relu、Maxout或者一些新兴激活函数。在DNN的计算中，每一层的输出都只受到前一层输入的影响，假设一个特征向量记为γ，计算出从第1层到第L-1层的激活向量，并通过分类计算，得到最终的输出结果，这个过程称为前向计算。传统的DNN分类函数一般选用Softmax函数来进行特征的归一化，其表达式如式(4)所示：

(4)

在进行DNN参数训练的时候，常用的训练方法为误差反向传播方法BP(Back Propagation)，将拥有一定隐藏层的DNN从一个输入空间映射到输出空间，其表示如式(5)所示:

RI→RO

(5)

其中，R表示向量空间。

在训练的过程中需要一定的训练准则及学习算法。常用的训练准则有均方误差MSE(Mean Square Error)准则和交叉熵CE(Cross Entropy)准则。根据不同的应用场景，训练准则的选取也有差异，对于回归任务，一般采用MSE准则，如式(6)所示:

(6)

其中，S={(om,ym)|1≤m

(7)

确定了训练准则后，通过误差反向传播算法进行学习。假设隐藏层采用的激活函数为Sigmoid函数，误差经过i层回传，此时第l层误差的表达式如式(8)所示:

(8)

其中Q为损失函数。采用梯度下降算法更新参数，迭代更新表达式如式(9)和式(10)所示:

(9)

(10)

其中ξ为学习率,通常根据经验获得。进而可求得网络参数的梯度如(11)和式(12)所示：

(11)

(12)

3 DNN声学模型

DNN系统通常基于训练数据和测试数据满足一个相同的概率分布的假设条件，该特性类似于其它机器学习技术。然而在语音识别时，由于说话人和说话环境通常处于一个多变的状态，这个假设通常难以满足，导致训练数据与测试数据之间不匹配。基于该原因，DNN自适应技术应运而生。不同于传统混合高斯模型，DNN为鉴别性模型，应用于二者的自适应方式有所不同。通常DNN自适应方式可归结为线性变换、保守训练及子空间法[14]，如图2所示。

Figure 2 Classification of DNN adaptive technology 图2 DNN自适应技术分类

(13)

其中N0为输入层大小。其变换后的网络结构如图3所示,图中方框中的部分为添加的线性隐藏层。

Figure 3 DNN structure after linear changed图3 线性变化后的DNN结构

线性变换法虽然取得了不错的自适应效果，但是仍然无法突破DNN固有特性的限制，有学者提出通过调整所有参数来改善这种限制，但是该种方式被证实会破坏DNN之前学习到的信息。保守训练是解决该问题的方式，一般采用L2正则项或者KL(Kullback-Leibler)距离正则项的方式对自适应准则进行约束。另外一种DNN的自适应方式为子空间方法，子空间法将说话人特征信息映射到一个特定的子空间中，利用神经网络的权值或自适应变换将其作为参数空间的一个数据点，然后进行自适应网络的构建。主成分分析法、噪声感知和张量基等都是这个领域中比较有前景的技术。

3.1 改进正则化自适应准则

L2正则化通过添加惩罚项来约束自适应准则，假设自适应模型W是由说话人无关模型VS经过一个自适应准则J(W,β;S)得到的，则:

(14)

其中，vec(VS-W)是矩阵VS-W中所有的列向量连接起来得到的向量。引入L2正则项约束，得到约束后的自适应准则,如式(15)所示:

JL2(W,β;S)=J(W,β;S)+ηR2(VS,W)

(15)

其中，η为正则项参数，通过L2正则项约束后，自适应后的模型与说话人无关模型之间参数的波动范围将得到有效限制。

KL距离正则项的目的在于避免自适应模型估计的senone后验概率与未自适应模型估计的后验概率差距过大。KL距离可以良好地衡量概率间差异，与DNN输出为概率分布特性相吻合。因此，将KL距离作为一个约束项添加到自适应准则中，去除模型无关项后，得到KL正则化优化准则，如式(16)所示:

JKL(W,β;S)=(1-η)J(W,β;S)+

ηRKL(VS,βS;W,β;S)

(16)

其中:

RKL(VS,βS;W,β;S)=

(17)

其中,PS(i|om;VS,βS)为说话人无关DNN中估计出的第m个观测样本属于类别i的概率，P(i|om;W,β)为自适应DNN第m个观测样本om属于类别i的概率。概率可通过交叉熵准则得到。为了充分结合L2正则项及KL正则项的优点，本文对正则化自适应准则进行改进，突破传统单一正则约束的限制，将二者进行结合，提出加权平均正则化方法，得到新型正则化约束表达式,如式(18)所示:

RKL(VS,βS;W,β;S)]}

(18)

其中，λ′为改进后的正则化权重。

3.2 特征子空间估计参数建模

在改进正则化自适应准则后，利用自适应后的权值估计一个特定说话人矩阵，记为FA∈Rm×n，该矩阵可被认为是在m×n维说话人子空间中的一个随机变量的观察值。假设n个说话人的均值超矢量如式(19)所示:

(19)

则所有说话人超矢量表示为f={τ(d)|d=1,2,…，n}构成了一个说话人子空间，然后对f进行主分量分析，由PCA近似得到的特征向量线性组合来表示新的说话人自适应矩阵。在这个特征子空间中维数最大为n，主分量分析之后得到p个基矢量。为了突破传统说话人子空间只能在自适应前确定的局限性，本文借鉴文献[15]中的子空间动态选择方式，采用最大似然准则代替传统加权系数的选择方式[15]，针对每个说话人选择最优的子空间，得到说话人的超矢量最大似然估计。

3.3 改进DNN输出层分类激活函数

前文提到，DNN在训练完毕后，通过输出层得到最终的结果输出，可以把这个输出结果理解为概率，一般选用Softmax函数进行归一化处理，因此多分类之后的概率之和也为1。图4所示为Softmax归一化处理的过程。

Figure 4 Softmax normalization process图4 Softmax归一化过程

假设x0,x1,…,xn为若干个输入语音特征，经过Softmax函数之后得到若干个[0,1]的数字输出，且P(x0)+P(x1)+…+P(xn)=1。Softmax函数表示如式(20)所示:

(20)

其中,q为训练数据所属类别。Softmax降低了训练的难度，并且在一定程度上抑制了过拟合现象的发生，但是并未保证类内紧凑、类间分离的特性。因此，仅仅使用限定的训练集显得微不足道。由于Softmax损失采用cosine距离作为分类预测标准，因此预测标签由各个类的角度相似性决定，因此本文引入文献[16]中的L-Softmax方式进一步优化Softmax，从而使所学特性之间存在更大的角分离性[16]。优化后的Softmax表达式如式(21)所示:

LL-Softmax=

(21)

其中,Wyi表示全连接层W的yi列，xi表示第i个输入。θj是Wj和xi之间的角度，θyi是Wyi与xi之间的角度。

(22)

经过优化之后的L-Softmax不仅有利于分类，并且保证了样本类内紧凑、类间分离的特性。另外，考虑到Softmax函数涉及指数运算，在计算机上进行运算时，可能会出现数据溢出导致结果异常的情况，因此对式(22)实行进一步的改进，通过分子分母同乘一个常数的方式，既能限制数据带宽又能保持结果不变。改进后的Softmax函数记为LC-Softmax函数，其表达式如式(23)所示:

LLC-Softmax=

(23)

其中H为常数。

4 复杂环境下的DNN语音识别

在搭建完整的模型框架之后，需要进一步考虑说话人及环境变化对系统产生的影响。在传统的GMM-HMM系统中，采用声道长度归一化VTLN(Vocal Tract Length Normalization)和特征空间最大似然回归fMLLR(feature-space Maximum Likelihood Linear Regression)克服说话人多样性[17]带来的问题。fMLLR本质上是作用在特征向量上的仿射变换，将其运用在测试集上，输入原始特征生成识别结果，利用识别结果估计fMLLR，变换后得到新的特征再进行识别。为了克服环境变化，传统的GMM系统通常采用向量泰勒级数VTS (Vector Taylor Series)、自适应和最大似然线性回归。然而由于DNN本质上为生成鉴别式模型，传统的克服说话人及环境多样性的方式需要进一步扩展。依据DNN特性，本文引入i-vector技术来克服说话人差异信息对特征的影响，此过程不仅可以减少说话人差异产生的影响，同时可将语义信息进行保留。引入噪声感知训练自动学习带噪语音与噪声到状态标注的映射关系，在一定程度上可减轻环境变化对语音识别率的影响。

4.1 i-vector技术分析及应用

i-vector技术的基本原理可以表述为：首先将描述说话人最重要的特征信息进行压缩，然后将压缩后的特征信息在一个低维固定长度中表示出来。利用i-vector良好的区分说话人信息的能力，去除语音特征中的说话人信息,保留需要的语义信息。另外，i-vector构建了一个独立的变换子空间来对语音信号的变化进行建模，其中语音信息包括说话人信息及信道信息变换。其表达式如式(24)所示:

Cs=k+Dws

(24)

其中，Cs为说话人均值超矢量;k为UBM(Universal Background Model)超矢量，UBM表示一个通用的背景模型;D表示总体变化子空间矩阵，将均值超矢量映射到低维，得到低维矢量ws。关于i-vector的计算文献[18,19]中有详细描述。将i-vector向量融入DNN结构中，如图5所示，图中w1,w2,…,wn为提取出的特定人i-vector，并且都相等。x1,x2,…,xn为说话人每一帧输入语音信息，然后将i-vector与原始输入语音信息进行拼接。如前所述，融合i-vector后的DNN结构由于保留了需要的语义信息，因此对说话人变化识别具有更强的鲁棒性，在一定程度上降低了语音识别错误率。

Figure 5 DNN structure fused with i-vector 图5 融合i-vector的DNN结构

4.2 噪声感知训练

前文提到，在传统的基于GMM的声学模型中，采用VTS、MLLR等方法可在一定程度上克服复杂多变环境的影响。在VTS方法中，自适应语音识别器的高斯参数常用一个估计噪声模型进行自适应，假设带噪语音信号表示为XN，纯净语音信号为Xc，噪声信号表示为N，那么语音和噪声之间的关系在对数频域中可近似表示为:

XN=Xc+log(1+exp(N-Xc))

(25)

在GMM系统中采用一阶VTS来近似表示这个非线性关系，然而，DNN具有多层的非线性变换，可以对任意的非线性关系直接进行建模。实际上我们关心的是带噪语音信号及噪声信号到纯净语音之间的非线性映射。通过噪声估计带噪语音信号与噪声信号到纯净语音信号的映射关系，克服多变噪声环境对识别系统产生的影响。

5 实验结果及分析

5.1 实验数据集及评估指标

为了验证本文算法的有效性，选取TIMIT和微软语料库作为实验数据来源。其中TIMIT为英文语料库，包含630个不同说话人信息，为评价说话人识别系统中最权威的语音数据库[20]。本文选取430个说话人语音组成训练集，选取40个说话人语音组成测试集，并且训练集与测试集间无重叠。中文语料库选择微软语料库，微软语料库是由微软亚洲研究院在2001年发布的用于搭建、测试中文连续语音识别系统的中文语料库。该语料库的训练集包含100个男性说话人信息，其中每个人说话语音为200段，共19 688段，总时长为33 h。说话人籍贯遍布全国26个省，测试集为北京方言口音，采用汉语有调音节进行标注[21]。

实验采用词错率WER(Word Error Rate)作为算法的评价指标,其表达式如式(26)所示:

(26)

其中，SW为语音解码时，连续语音与人工标注统计出的替换词的个数;DW为删除词的个数;IW为插入词的个数;NW为语音库中正确词的总数量。该指标数值越低，系统性能越高，语音识别率越高。

5.2 实验环境及参数配置

本文在Kaidi语音识别工具上进行开发和实验。首先搭建GMM-HMM模型，选取13维MFCC特征与其一阶差分、二阶差分共39维作为GMM-HMM的输入量。针对浅层模型，如HMM、GMM等一般采用MFCC、LPCC等特征参数，FBANK特征因其携带更多的特征信息，更加适合作为深层训练模型的特征参数，因此DNN模型及本文自适应DNN模型皆选取FBANK特征。一般来说，语音信号窗长在10～30 ms认为是稳态的，即语音信号具有短时平稳性，因此窗长选择一般在这个范围即可，本文取窗长为25 ms，帧移选取通常在5～15 ms，本文取其中间值10 ms作为帧移长度。实验中整个DNN框架输入层、隐藏层和输出层的个数分别为1，5和1。其中隐藏层包含2 048个节点，输出层采用LC-Softmax进行归一化处理。另一方面，在对深度神经网络进行参数调节的过程中，需要根据训练集与测试集识别率的比对来控制迭代次数，参数初始化完毕后，对自适应模型进行迭代，训练集与测试集得到的语音识别率与迭代次数的关系如图6所示。

Figure 6 The relationship between the recognition rate and the number of iterations图6 识别率与迭代次数关系

5.3 对照实验及分析

本文采用目前语音识别中常见的GMM-HMM及传统DNN声学模型作为对照组，与本文自适应DNN模型进行比较。在训练GMM-HMM时，将上下文相关的三音素融入模型中，训练完毕后，将输出特征进行解码。在采用自适应DNN模型时，为了保证在词错误率尽可能低的情况下训练时间也不至于过长，对DNN隐藏层数量及节点个数的选取进行了若干组实验。隐藏层数对词错误率的影响如图7所示。从图7可以看出，随着隐藏层数量的增加，单词错误率明显降低，说明在一定范围内增加隐藏层数可以提升语音的识别率。但是，当隐藏层数量继续增加的时候，错误率又呈现上升的趋势，可见过多的隐藏层数会导致数据出现过拟合的现象，导致识别率降低。因此，本文选择自适应DNN声学模型结构中的隐藏层数为5。

Figure 7 The influence of hidden layers on word error rate of the model图7 隐藏层数对模型词错误率的影响

为了确定隐藏层节点个数，实验在5层隐藏层时，分别对隐藏层节点个数为1 024,2 048和4 096进行耗时和语音识别率的统计，结果如图8所示。由图8可以看出，当隐藏层节点个数增加时，系统耗时和识别正确率均处于上升的趋势，但是当节点数目大于2 048时，实验耗时急剧增加，而识别正确率虽然呈现上升的趋势，但是上升幅度不大。综合时间及识别性能等多种因素，本文选择隐藏层节点个数为2 048，在保证识别性能的前提下，避免过多的时间消耗。

Figure 8 The influence of the number of hidden nodes on the system model图8 隐藏层节点数对系统模型的影响

为了验证多噪声下系统的语音识别性能，在进行性能测试时，引入NoiseX-92噪声库中的Babble、F16、Street和Factory 4种类型的噪声作为背景噪声。NoiseX-92噪声库是由英国感知技术研究院在实地测量所得到的噪声数据库，能够很好地模拟现实环境中的噪声干扰。然后对不同声学模型分别在4种噪声下调节不同信噪比进行多次对照实验，表1和表2分别为在TIMIT英文语音数据集和微软中文语音数据集上不同模型的词错误率统计。

Table 1 Comparison of WER of different models on the TIMIT data set

由表1和表2可以看出，2种数据集上，WER的变化趋势基本一致。相对于GMM-HMM模型，深度神经网络模型以及本文自适应深度神经网络模型的WER均呈现下降的趋势。整体上看，无论是在TIMIT英文语音数据集还是微软中文语音数据集，在多种背景噪声下，WER随着信噪比的增加而增大，说明环境信噪比低会严重影响系统的语音识别率。高斯混合模型和传统DNN模型，未考虑说话人及环境噪声变化引起的噪声训练与测试数据不匹配，因此WER普遍偏高。将i-vector及噪声感知融入DNN模型后，得到的模型能够自适应处理训练及测试数据之间不匹配的问题，因此WER相对较小。对比可知，TIMIT数据集上，在Babble、F16、Street和Factory 4种噪声下本文算法相较于GMM-HMM模型平均WER分别下降了3.818%,5.653%,5.257%和5.875%。相较于传统DNN模型平均WER分别下降了1.030%,3.740%,3.798%和3.885%。可以看出无论是在中文语音数据集还是英文语音数据集上，词错误率均有所下降，本文自适应DNN模型的泛化性能及鲁棒性相较于对比模型均有一定程度的提高。

Table 2 Comparison of WER of different models on the Microsoft voice data set

6 结束语

本文提出了一种复杂环境下基于自适应深度神经网络的语音识别。针对说话人及环境多变性造成训练数据与测试数据不匹配造成的识别率低的问题，改进自适应准则并与特征空间相结合，提高数据的匹配度。通过对GMM-HMM及传统DNN模型分别在多种背景噪声下进行对比实验，结果表明本文自适应DNN声学模型在TIMIT中文语音数据集、微软中文语音数据集上，平均WER分别下降了5.151%和3.113%，表明本文自适应DNN模型拥有更强健的建模能力。