一种基于信息测度的多属性决策方法

魏丽君,吴海波,章若冰

(1.中南大学自动化学院,湖南 长沙 410001; 2.湖南铁道职业技术学院,湖南 株洲 412001)

0 引 言

熵、相似性测度和交叉熵是模糊理论中的3个重要的研究领域，在信息融合系统、医学诊断等领域有着广泛的应用。熵对于测量不确定信息非常重要。从熵出现以来，它受到了广泛的关注。Zadeh首先引入了模糊熵的概念来衡量决策信息的模糊性。此外，Luca和Termini提出了模糊熵应该遵循的原理[1-8]，Szmidt和Kacprzyk基于直觉模糊基数的比值，给出了直觉模糊熵测度的原理化要求，并提出了一种IFSS的非概率型熵测度方法[9-10]。Ye提出了2种IVIFS的熵度量方法，并建立了一个熵权模型来确定熵的权重[11-12]。Jin等人基于连续有序加权平均(COWA)算子研究了区间值直觉模糊连续加权熵来处理MADM问题。而Majumdar和Samant引入了熵函数来测量SVNV中涉及的不确定性[13]。

相似性测度和交叉熵主要用于识别信息的度量，当前已经对此进行了大量研究，对熵定义、距离度量和相似度量都进行了详细的阐述，并讨论了它们之间的基本关系。Vlachos和Sergiadis提出了直觉模糊交叉熵的概念，并讨论了交叉熵和熵之间的关系。Beliakov等人研究了一种定义IFSS相似性度量的新方法[14-18]，其中相似性度量包含相似性和犹豫性2个部分。Ye提出了在SVNSS之间获得MADM问题中所有备选方案的排序顺序的3种向量相似度测度方法，并在相似性度量缺点的基础上，基于余弦函数，构造了SVNSS的修正余弦相似性度量[19-21]。Majumdar和Samant根据2个SVN之间的距离提出了几种SVN的相似性度量方法[22-24]，并讨论了它们的特点。

本文基于模糊熵、相似测度和交叉熵的概念引入单值中智信息函数信息测度的3个公理化定义，并基于余弦函数构造其信息测度公式，讨论支持向量网络的这些信息测度之间的关系，在此基础上研究一种MADM方法。

1 单值中智信息测量

1.1 单值中智集的熵

SVNS的熵由Majumdar和Samant(2014)[17]定义如下：

定义1 SVNS的熵A={〈x,TA(x),IA(x),FA(x)〉|x∈X}是满足以下公理的函数：ε:A→[0,1]。

1)ε(A)=0，如果A是一个明确集。

2)ε(A)=1，如果〈x,TA(x),IA(x),FA(x)〉=〈0.5,0.5,0.5〉，∀x∈X。

3)ε(A)=ε(Ac)。

4)ε(A)≥ε(B)，如果A比B更不确定，即：

TA(x)+FA(x)≤TB(x)+FB(x)并且|IA(x)-IAc(x)|≤|IB(x)-IBc(x)|。

然而，在某些情况下，定义1中的公理化需求4可能是不切实际的。因此，SVNSS的熵定义需要改进。

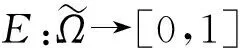
1)E(α)=0当且仅当αt=0或者αt=1，t=1,2,3。

2)E(α)=1当且仅当〈α1,α2,α3〉=〈0.5,0.5,0.5〉。

3)E(α)=E(αc)。

4)E(α)≤E(β)，如果β比α存在更不确定性，即αt≤βt当βt-βtc≤0，t=1,2,3或者αt≥βt当βt-βtc≥0，t=1,2,3。

基于余弦函数，构造了SVNVS的信息测度公式如下：

(1)

1.2 单值中智相似度测度

定义3 假设α和β是2个SVNVS，α和β之间的相似性度量表示为S(α,β),应满足以下公理要求：

1)当且仅当αt-βt=1或者αt-βt=-1时，S(α,β)=0，t=1,2,3。

2)当且仅当〈α1,α2,α3〉=〈β1，β2，β3〉时，S(α,β)=1。

3)S(α,β)=S(β,α)。

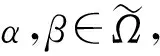
(2)

则等式(2)定义的映射S1(α,β)是α和β之间的相似测度。

1.3 单值中智交叉熵

定义4 假设α和β是2个SVNVS的α和β之间的单值中智交叉熵，表示为C(α，β)，应满足以下2个公理要求：

1)C(α，β)≥0。

2)C(α，β)=0⟺〈α1，α2，α3〉=〈β1，β2，β3〉。

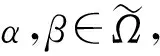
(3)

由等式(3)定义的映射C1(α，β)是α和β之间的交叉熵。

2 单值中智熵、相似测度和交叉熵之间的关系

令α为一个SVNV，那么S(α，αc)是其单值中智子熵，即：

E(α)=S(α，αc)

(4)

这足以证明S(α，αc)满足定义2中列出的要求1～4。

1)E(α)=0⟺S(α，αc)=0⟺αt-αtc=1或者αt-αtc=-1，t=1,2,3，即：

αt-(1-αt)=1或者αt-(1-αt)=-1，t=1,2,3

(5)

所以，若式(5)成立，则：αt=0或αt=1，t=1,2,3。

2)E(α)=1⟺S(α，αc)=1⟺〈α1，α2，α3〉=〈α1c，α2c，α3c〉

⟺〈α1，α2，α3〉=〈1-α1，1-α2，1-α3〉

⟺αt=1-αt,t=1,2,3⟺αt=0.5,t=1,2,3

⟺〈α1，α2，α3〉=〈0.5，0.5，0.5〉。

3)E(αc)=S(α，αc)c=S(αc,α)=S(α，αc)=E(α)。

4)如果αt≤βt，当βt-βtc≤0,t=1,2,3，可得βt-(1-βt)≤0,t=1,2,3，即：

βt≤1-βt,t=1,2,3，可得：

αt≤βt≤1-βt≤1-αt,t=1,2,3，即：

αt≤βt≤βtc≤αtc,t=1,2,3。

因此可以推断:S(α，αc)≤S(β，αc)≤S(β，βc),即：E(α)≤E(β)。

同样，如果αt≥βt，当β-βc≥0,t=1,2,3时，可得E(α)≤E(β)。

因此可以推出，令α是一个SVNV，则：

E1(α)=S1(α，αc)

(6)

令α和β是2个SVNV，则1-S(α，β)是其单值中智交叉熵，即：

C(α，β)=1-S(α，β)

(7)

1)因为单值中智相似度量S(α，β)∈[0,1]，所以：

C(α，β)=1-S(α，β)∈[0,1]

(8)

很明显，C(α，β)≥0。

2)C(α，β)=0⟺1-S(α，β)=0⟺S(α，β)=1，当且仅当〈α1，α2，α3〉=〈β1，β2，β3〉时，S(α，β)=1。

令α和β是2个SVNV，则：

C1(α，β)=1-S1(α，β)

由此可以得到如下定理：

定理1 令α是一个SVNV，则1-C(α，αc)是其单值中智熵，即：

E(α)=1-C(α，αc)

推论1 令α是一个SVNV，则E1(α)=1-C1(α，αc)。

3 单值中智信息测度的MADM方法

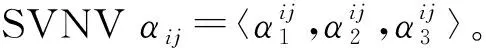
3.1 确定属性权重的方法

为了得到最优的选择方案，首先提出一种基于熵和交叉熵的属性权重向量确定方法。一方面，考虑属性Cj的熵，属性Cj的平均熵E(Cj)如下：

(9)

每个E1(αij)可通过式(1)计算。根据熵理论，一个属性的熵在不同的选择中是较小的，然后该属性应该被赋予更大的权重。

另一方面，对于属性Cj，备选方案Xi对所有其他备选方案的平均交叉熵可以表示为：

(10)

属性Cj的平均交叉熵可以表示为：

(11)

其中每个Cj，C1(αij,αkj)可以通过式(3)计算。众所周知，一个属性的交叉熵越大，那么该属性就应该被赋予一个更大的权重。如果属性Cj,j=1,2,…,n的权重wj的信息完全未知，则可以使用以下的熵权方法来确定属性权重：

(12)

属性Cj,j=1,2,…,n的权重wj的信息可以通过构造以下优化模型以获得最优权重向量：

(13)

3.2 基于信息测度的MADM方法

在MADM问题中，让X+={α1+,α2+,…,αn+}和X-={α1-,α2-,…,αn-}分别作为它们的交易替代品和反理想替代品，其中αj+=〈1,0,0〉，αj-=〈0,1,1〉，j=1,2,…,n。

基于上述分析，本文提出一种单值中智环境下的MADM方法，其主要步骤如下：

(14)

Step2利用等式(12)或模型(13)确定属性的权重向量：W=(w1,w2,…,wn)。

(15)

(16)

Step4计算方案Xi与理想方案的接近度为：

(17)

Step5按降序排列所有接近度T(Xi),i=1,2,…,m。

Step6根据接近度T(Xi),i=1,2,…,m选择最佳备选方案。最好的选择是最大maxT(Xi)，i=1,2,…,m。

Step7结束。

4 验证实例

利用本文所提出的方法对该MADM问题进行处理。主要步骤如下：

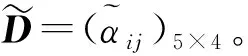
Step2由于属性Cj(j=1,2,3,4)的权重wj信息完全未知，因此利用等式(12)计算属性的权重向量，如下所示：

w1=0.2107，w2=0.3011，w3=0.1067，w4=0.3815

Step3利用式(15)和式(16)确定城市Xi与理想城市X+和反理想城市X-之间的相似性度量：

S+(X1)=0.3317，S+(X2)=0.3845，S+(X3)=0.5319，S+(X4)=0.4486，S+(X5)=0.3627，S-(X1)=0.4481，S-(X2)=0.3977，S-(X3)=0.2885，S-(X4)=0.3419，S-(X5)=0.4240

Step4利用式(17)得到城市Xi与理想城市的接近度T(Xi)(i=1,2,3,4,5)：

T(X1)=0.4254，T(X2)=0.4916，T(X3)=0.6483，T(X4)=0.5675，T(X5)=0.4610

Step5由于T(X3)>T(X4)>T(X2)>T(X5)>T(X1)，可得到Xi(i=1,2,3,4,5)的排名是X3>X4>X2>X5>X1，受雾霾污染最严重的城市是X3。

Step6结束。

下面，采用文献[11]提出的方法进行比较研究。利用文献[11]的方法来处理上述问题，具体的决策步骤如下：

Step1同上Step1。

Step2利用SVNA和B之间的相似性度量公式(即文献[11]中的等式(6))：

可以得到城市Xi和理想城市X+之间的相似性度量T(Xi,X+)(i=1,2,3,4,5)：

T(X1,X+)=0.2301，T(X2,X+)=0.1413，T(X3,X+)=0.3561，T(X4,X+)=0.2639，T(X5,X+)=0.2381

Step3根据相似性度量的结果，得出：

T(X3,X+)>T(X4,X+)>T(X5,X+)>T(X1,X+)>T(X2,X+)

那么所有城市Xi(i=1,2,3,4,5)的排名是X3>X4>X5>X1>X2。因此，受雾霾污染最严重的城市是X3。

根据上述实例，与文献[11]提出的方法相比，本文提出的方法具有以下一些优势。

1)本文提出的MADM方法的应用范围较文献[11]更广。此外，本文所提出的MADM方法可以管理决策信息为SVNVS的问题。

2)本文的方法以信息度量为重点，文献[11]提出的方法以距离度量为重点，这2种方法都适合处理备选方案权重向量未知的情况。然而，本文所提出的MADM方法得到的排序结果更合理和可信。

3)在决策过程中，采用MADM方法得到排序结果，考虑了所有决策信息，但文献[11]提出的排序结果会导致信息丢失，因为采用了豪斯多夫距离，忽略了一些中间值。因此，本文提出的MADM方法可以得到更准确的结果。

5 结束语

目前，许多信息测度方法应用于MADM问题，但这些方法不能用来处理单值中智MADM问题。在单值中智环境下，本文介绍了信息测度的3个公理化定义，包括熵、相似测度和交叉熵，在余弦函数的基础上构造了信息测度公式，然后讨论了单值中智信息测度之间的关系，并在此基础上提出了一种处理MADM问题的新方法。最后，通过数值算例验证了该方法的有效性。