滚动轴承振动性能序列动态预报研究*

邵立东,常 振,陆水根,曹茂来

(1.杭州职业技术学院 吉利汽车学院,浙江 杭州 310018;2.杭州轴承试验研究中心有限公司,浙江 杭州 310022;3.机械工业轴承产品质量检测中心,浙江 杭州 310022)

0 引 言

滚动轴承是机电行业中应用最为广泛的基础件与精密件之一,如何确保其在各类复杂的环境中正常运转,并准确高效地完成其规定功能,是轴承维护过程中的重点与难点。

由于滚动轴承寿命的离散性较大,定期更换或保养并不可行;而滚动轴承振动信号是监测其性能失效的重要指标,因此根据振动性能判断分析轴承运转状况变得十分必要[1,2]。

从服役开始至失效结束,轴承退化史是一个渐变的过程,在轴承发生异常行为或故障之前,其振动信号可能早有预示。及时有效地对滚动轴承振动性能进行预报和诊断,可提醒机修人员在轴承损坏之前采取相应的维护或保养措施,进而避免机组失效、生产停滞,甚至人员伤亡等恶性事故的发生[3,4]。

然而,滚动轴承振动信号成分虽然具有明显的随机性及不确定性,基于已知概率密度函数的传统统计理念的分析方法难以奏效,但其中确实又隐含有轴承健康状况的潜在信息和确定性规律。

诸多学术界与工程界研究者对如何基于振动信号进行轴承状态监控及预报做了研究,并已获得了一些可行性方法。

邓四二、张文平等人[5,6]搭建了滚动轴承的动力学数学模型,对不同表面特征参数(表面粗糙度、圆度、波纹度等)、工况参数,及谐波参数下滚动轴承的振动特性进行了理论分析。陈奕雅、GRASSO M等人[7-9]利用滚动轴承故障后的振动时间序列,对故障信号进行了特征提取,并根据二阶循环统计量、经验模式分解技术,实现了对轴承故障状况的有效识别及诊断。程金山等人[10]根据不同的润滑脂流变参数,测定出相应工况下的轴承振动值,研究了润滑脂的胶体结构、弹性模量、表观黏度等变化特性对轴承振动值的影响规律。李洪儒、SINGH S等人[11,12]针对轴承振动信号随机强、抗干扰能力差、波动剧烈等问题,提出了二元多尺度熵和多函数融合的滚动轴承退化趋势预测方法,可快速有效地进行轴承故障/失效预报。叶亮、SUN F等人[13-15]基于滚动轴承的振动信号提取出了轴承衰退性能指标,分别建立了数据驱动的可靠性与寿命预测模型,进而实现了滚动轴承可靠性与寿命的有效预测。

上述研究成果大都是针对轴承振动性能所进行的信号提取、故障诊断、状态分析等研究,而对其振动性能在未来状态下的演变预报的研究少之又少。

为了对轴承振动性能序列进行动态预报,笔者将自助法与最小二乘法进行有效融合,提出一种自助-最小二乘线性拟合的动态预报模型。首先,运用自助法将紧邻且不断更新的10个轴承振动数据进行10 000次仿真抽样,形成10 000个样本含量为10的振动序列;然后,将该振动序列用最小二乘法线性拟合,分别得到各自的线性拟合解a、c;其次,凭借最大熵原理对10 000组拟合解进行概率密度求取,在给定置信水平下得到相应的拟合真值与拟合区间;最后,根据未来时间变量实现滚动轴承振动性能真值与区间的动态预报。

1 研究方法

此处笔者设滚动轴承振动性能序列X为:

X=(x1,x2,…,xn,…,xN)

(1)

式中:xn—原始序列X的第n个振动数据;N—原始数据个数。

1.1 自助-最小二乘法

自助-最小二乘法是自助法与最小二乘法的融合。自助法可将一组数据等概率、可放回地抽样多次,进而构成多组数据;最小二乘法可将一组数据通过最小化误差平方和,寻找其函数的最佳匹配;二者的有效融合,可将一组数据进行多次拟合,进而获得多组数据的最小二乘解。

具体实施时,取紧邻的10个振动信号xi,xi+1,xi+2,…,xi+9,其中,i=1,2,…,N-9。以1,2,…,10为自变量,x为因变量,利用自助-最小二乘法进行线性拟合。

运用自助法,对紧邻的10个滚动轴承原始振动信号等概率、可放回地随机抽取1个数,共抽取q=10次,得到一个自助样本Y1,其有q=10个数据。按此方法重复执行B次,得到B个样本,可表示为:

YBootstrap=(Y1,Y2,…,Yb,…,YB)

(2)

式中:Yb—轴承振动信号的第b个自助样本,b=1,2,…,B;B—总的自助再抽样次数,也是自助样本的个数。

且有:

Yb=(y1,y2,…,yl,…,yq)

(3)

利用最小二乘法对Yb进行线性拟合:

Yb=abI+cb

(4)

且有:

I=(1,2,3,…,10)=(i1,i2,…,il,…,iq)

(5)

其中:i1～iq与数值1～10一一对应。

其最小二乘解为:

(6)

(7)

由于线性拟合共进行B次,则获得的B个最小二乘解，可表示为:

a=(a1,a2,…,ab,…,aB)

(8)

c=(c1,c2,…,cb,…,cB)

(9)

为了获得轴承振动信号自助样本的最小二乘解的估计真值a0、c0,以及上、下区间[aL,aU]和[cL,cU],笔者运用最大熵原理,分别对最小二乘解a和c进行概率度求取。

1.2 最大熵原理

1.2.1 概率密度求取

此处笔者以最小二乘解系数a为例,进行概率密度求取,将式(8)的B个系数a连续化,定义最大熵的表达式为:

(10)

式中:p(a)—连续化后的数据序列a的概率密度函数。

最大熵的主要思想是在所有可行解中,满足熵最大的解是最“无偏”的。最大熵方法能够对未知的概率分布做出主观偏见为最小的最佳估计。

通过调整p(a)可以使熵达到最大值,拉格朗日乘子法的解可表示为[16]:

(11)

式中:θ0,θ1,…,θβ—拉格朗日乘子;a—最小二乘解系数a的随机变量。

根据该概率密度函数p(a)可实现该数据序列的估计真值a0与上、下区间[aL,aU]的预报。

1.2.2 参数估计

由随机变量a的概率密度函数p(a),可得序列a的估计真值a0为:

(12)

对于双侧分位数,有概率:

(13)

(14)

式中:aU,aL—最小二乘解系数a的上界值和下界值;δ—实数,δ∈(0,1);[aL,aU]—δ水平下的置信区间[17]。

同理,可得到最小二乘解系数c的估计真值c0与上、下界[cL,cU]。所以,在自助-最小二乘法线性拟合时,根据最大熵原理,可实现最小二乘解的最优估计及上、下区间预报。将最小二乘解代入拟合方程(4),即可获得滚动轴承振动信号的最优估计值x0和上、下区间[xL,xU]。

1.3 步骤分析

具体的步骤如下:

(1)采用滚动轴承振动信号传感器,采集滚动轴承振动性能序列X;

(2)紧邻的10个轴承原始振动数据运用自助-最小二乘法线性拟合,获得样本含量为B的最小二乘解向量序列a和c;

(3)利用最大熵原理对序列a和c建立各自的概率密度函数,在给定置信水平下,求取最小二乘解的最优估计值a0、c0和上下限[aL,aU]、[cL,cU];

(4)再将最优估计值a0、c0和上下限[aL,aU]、[cL,cU]代入式(4)的线性拟合方程,设定自变量为11～20,进而预报出下一时间段(第11～20)的滚动轴承振动性能的真值x0及上、下区间[xL,xU];

(5)不断更新紧邻的10个轴承原始振动数据,重复步骤2、3、4,从而实现滚动轴承振动性能真值与上、下区间的动态预报。

2 实验及结果分析

由于这是一个超精密滚动轴承的寿命强化试验,此处笔者采用型号为ABLT-1A的试验机。该试验机主要由试验头、试验头座、传动系统、加载系统、润滑系统和计算机控制系统组成。

轴承寿命强化试验台架如图1所示。

图1 轴承寿命强化试验台架

试验样品为超精密滚动轴承H7008C,且该类轴承有一个过渡等级,尚可达到国标P2级的精度要求。试验在电机转速为4 950 r/min,室温为26 ℃,湿度为53%的环境条件下进行,所施加径向载荷为5 kN,轴向载荷2 kN。

试验头原理图如图2所示。

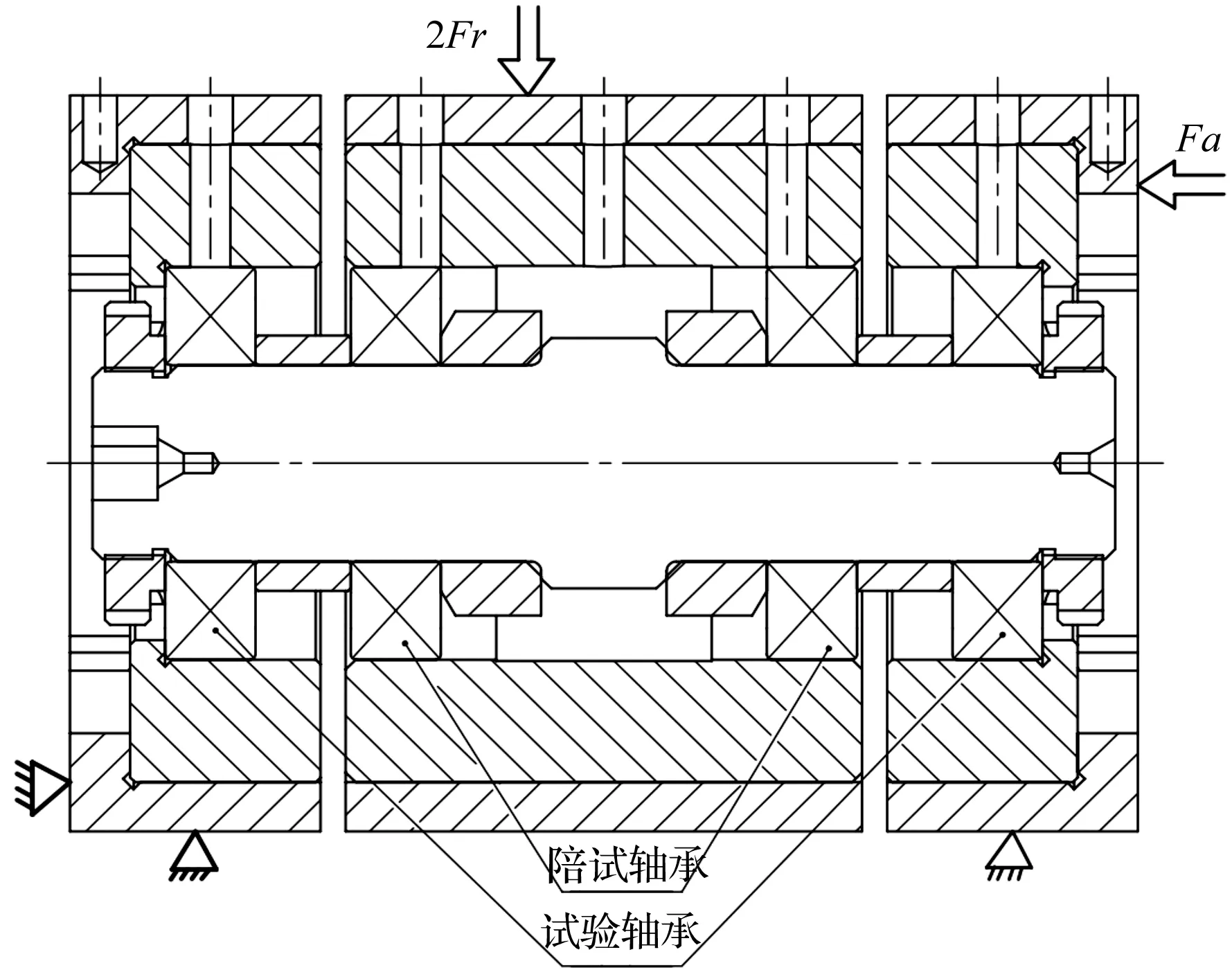
图2 轴承寿命试验头原理图

2.1 振动性能序列X采集

试验时间及轴承振动信息由计算机控制系统自动累积显示,每间隔10 min由传感器采集一次振动加速度信号,单位为ms-2。

笔者分别采集该型号轴承初期、中期、临尾3个服役时间状态下,振动加速度数据作为试验研究的案例。

初期振动时间序列记为XA,如图3所示。

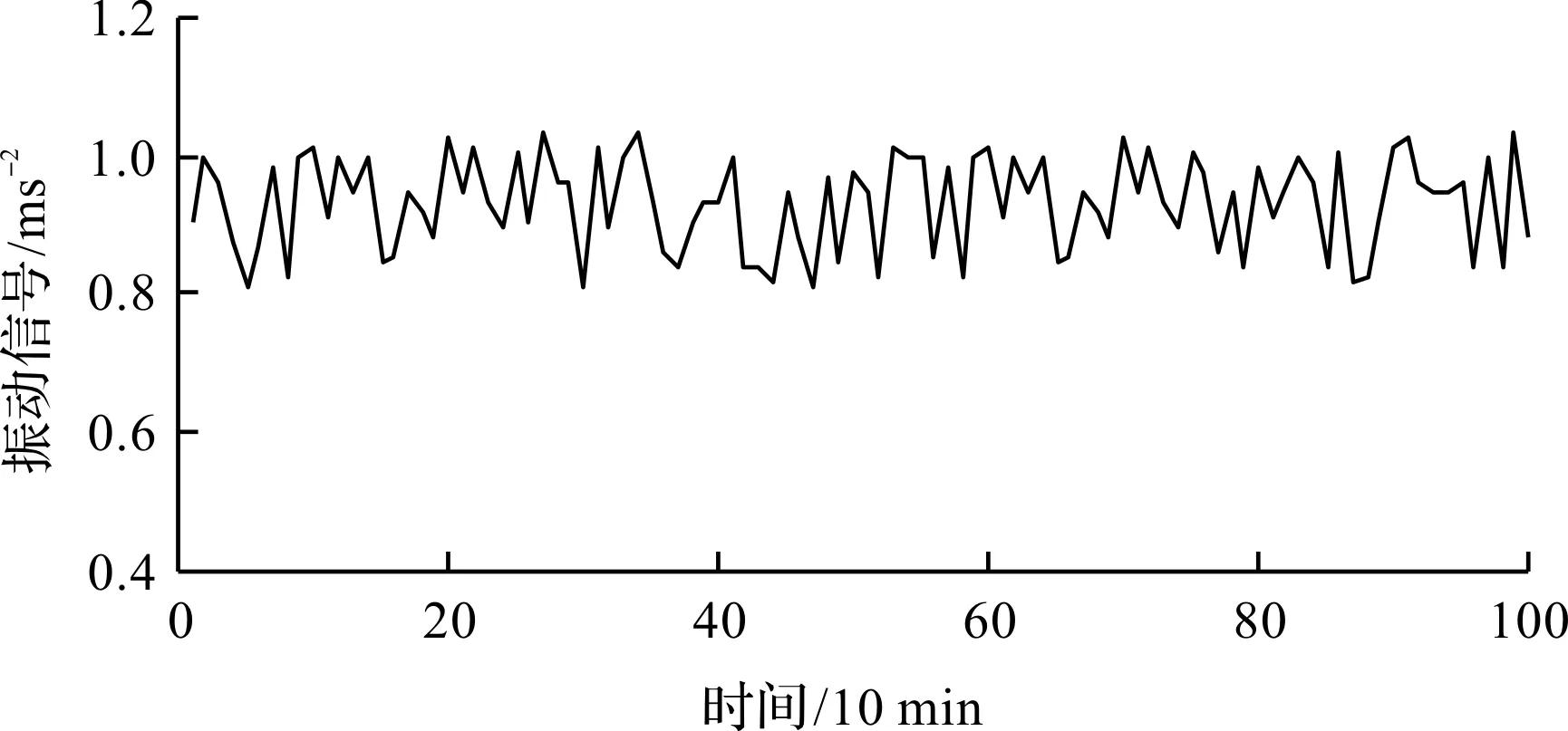
图3 轴承初期振动性能时间序列XA

中期振动时间序列XB,如图4所示。

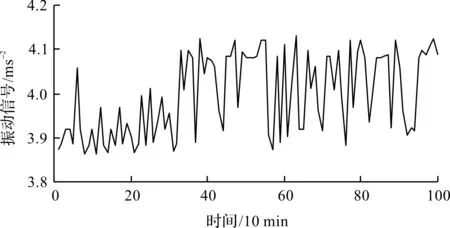
图4 轴承中期振动性能时间序列XB

临尾阶段的振动数据序列为XC,如图5所示。

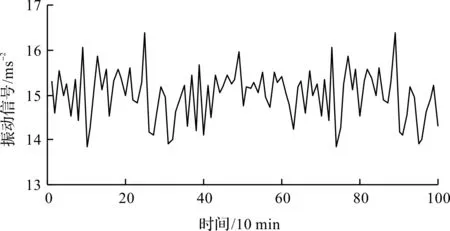
图5 轴承临尾振动性能时间序列XC

由图(3～5)的轴承振动原始数据不难看出:振动信号表现出明显的随机性及不确定性,难以用准确的公式或相应的概率分布函数对其进行描述;且不同服役阶段振动值的大小、波动区间、变化趋势各不相同,这对轴承振动信号的预报十分不利。

为有效地克服以上问题,笔者提出一种轴承振动信号预报模型,然后进行具体的数据分析处理。

2.2 自助-最小二乘法线性拟合

以初期振动性能时间序列XA为例,笔者将样本含量为100的XA序列等分成10组,即每组10个样本数据(x1-x10,x11-x20,…,x91-x100)。首先,以x1-x10为训练值进行有效预报,预报步长为10步:x1-x10内的10个数据运用自助法等概率、可放回地抽样10次,并连续重复10 000次,可构成样本含量为10 000的自助序列Ybootstrap=(Y1,Y2,…,Yb,…,Y10 000),其中,Yb的样本含量为10;再利用最小二乘法,对Yb内的10个抽样数据进行线性拟合,可分别得到拟合参数ab和cb;最后构成样本含量为10 000的最小二乘解序列a=(a1,a2,…,ab,…,a10 000)和c=(c1,c2,…,cb,…,c10 000)。

最小二乘解序列a结果如图6所示。

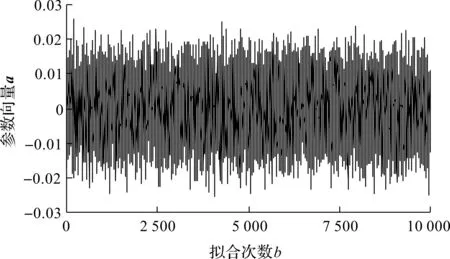
图6 时间序列XA中x1-x10的自助-最小二乘解序列a

最小二乘解序列c结果如图7所示。

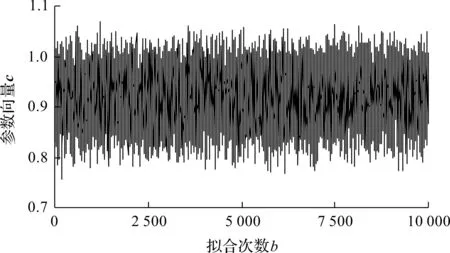
图7 时间序列XA中x1-x10的自助-最小二乘解序列c

2.3 最大熵概率密度求取

采用自助-最小二乘法进行线性拟合的方式,可由图(6～7)得到时间序列XA中x1-x10这10个紧邻的振动数据的解集a和c;再将B个解集连续化,得到其对应的最大熵表达式,即式(10);根据拉格朗日乘子法,可得到该轴承当前序列段的拟合系数a和c的概率密度函数,即式(11)。

在时间段XA中,轴承x1-x10的拟合系数a的概率密度函数,如图8所示。

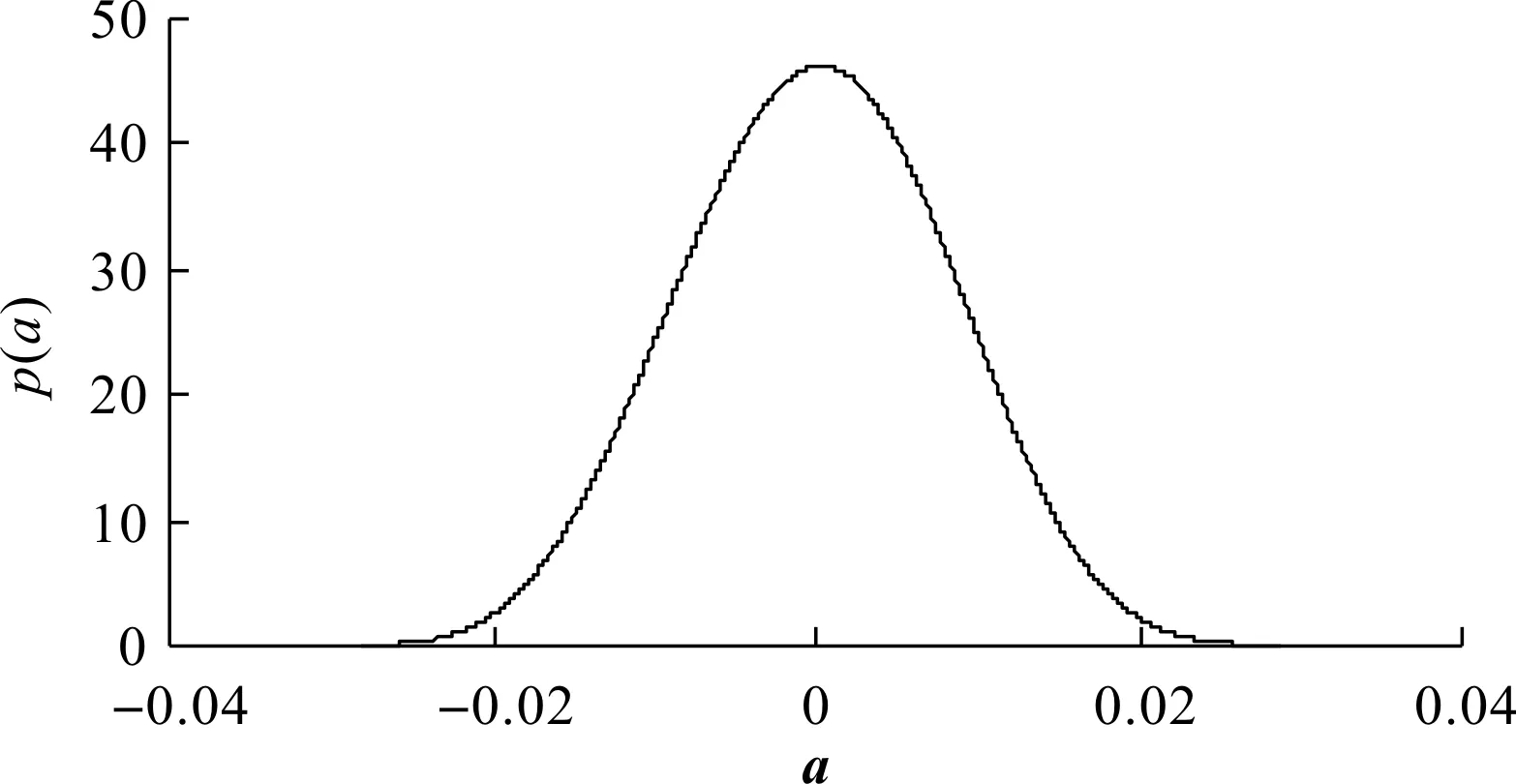
图8 时间序列XA中x1-x10的拟合系数a的概率密度图

在时间段XA中,轴承x1-x10的拟合系数c的概率密度函数,如图9所示。

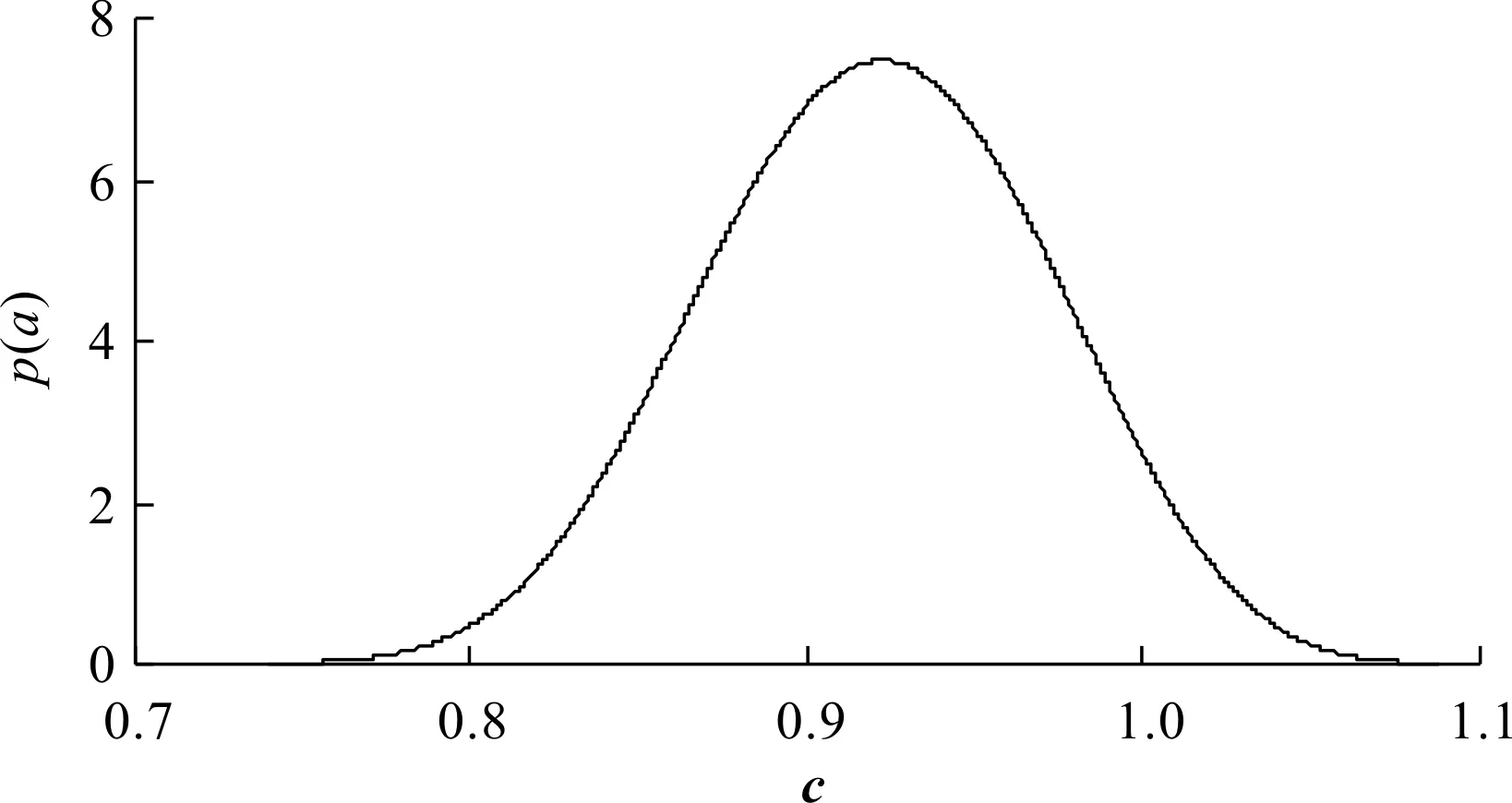
图9 时间序列XA中x1-x10的拟合系数c的概率密度图

接下来,需要对参数a和c进行估计。根据图(8,9)所得的自助-最小二乘解系数a和c的概率密度函数,结合式(12),便可得到其各自的估计真值a0和c0;然后给定显著水平δ=0.1(即置信水平为90%),根据式(13,14)得到其对应的区间上下限[aL,aU]和[cL,cU]。

所以,时间序列XA中x1-x10的拟合系数的预报结果,即系数a和c的估计真值与区间如表1所示。

表1 系数a和c的估计真值与区间

表1中的结果便是XA中,采用自助-最小二乘法进行线性拟合x1-x10这10个紧邻的振动数据的解,再分别将其代入线性拟合式(4),便可得到x1-x10这10个紧邻的轴承振动性能数据的拟合方程;令自变量等于11～20,便可获得第11～20个时间段(即未来时间段)振动性能的预报真值及上、下限。

在进行第21～30个时间段的振动性能预报时,采取旧数据舍弃、新数据更替的原则,将原来的x1-x10原始数据舍弃,添加10个新的原始振动性能值x11-x20;同时,将x11→新x1,x12→新x2,x13→新x3,…,x20→新x10,即将x11-x20这10个紧邻的原始振动数据转变为新的x1-x1010个振动性能数据;然后,重复以上步骤,对其进行自助-最小二乘法线性拟合;同样,令自变量等于11～20,便可获得第21～30个时间段振动性能的预报真值及上下限。

同理,依次类推,可分别得到第31～40,41～50,51～60,…,等时间段的线性拟合结果。

在各时间段内,时间序列XA的自助-最小二乘法拟合系数,如表2所示。

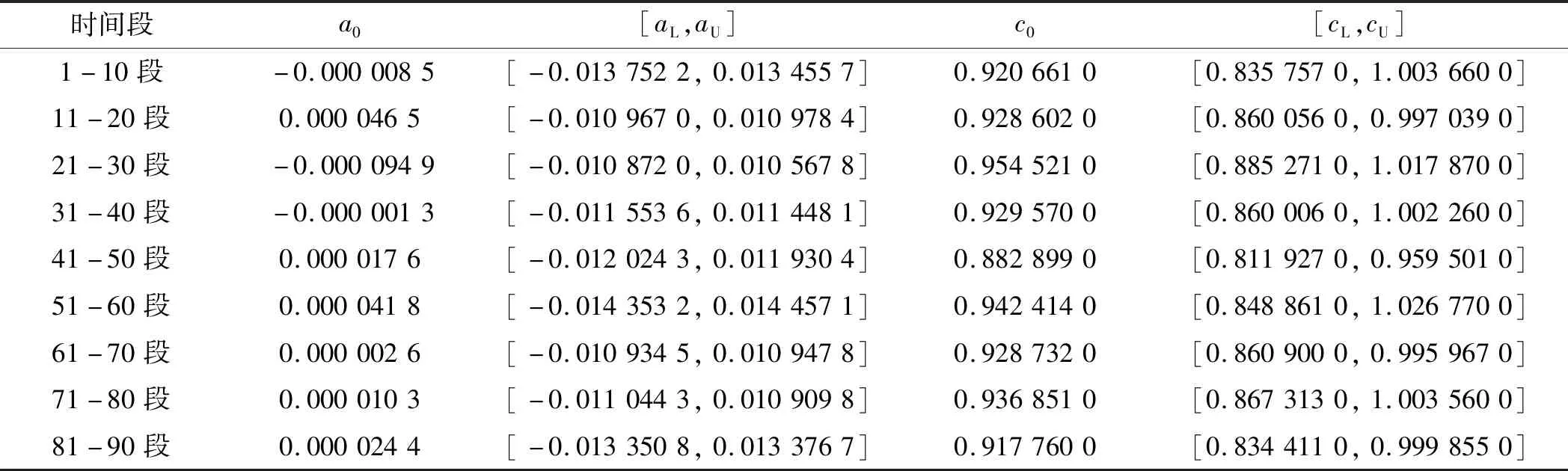
表2 时间序列XA的拟合系数

在各时间段内,时间序列XB的自助-最小二乘法拟合系数,如表3所示。

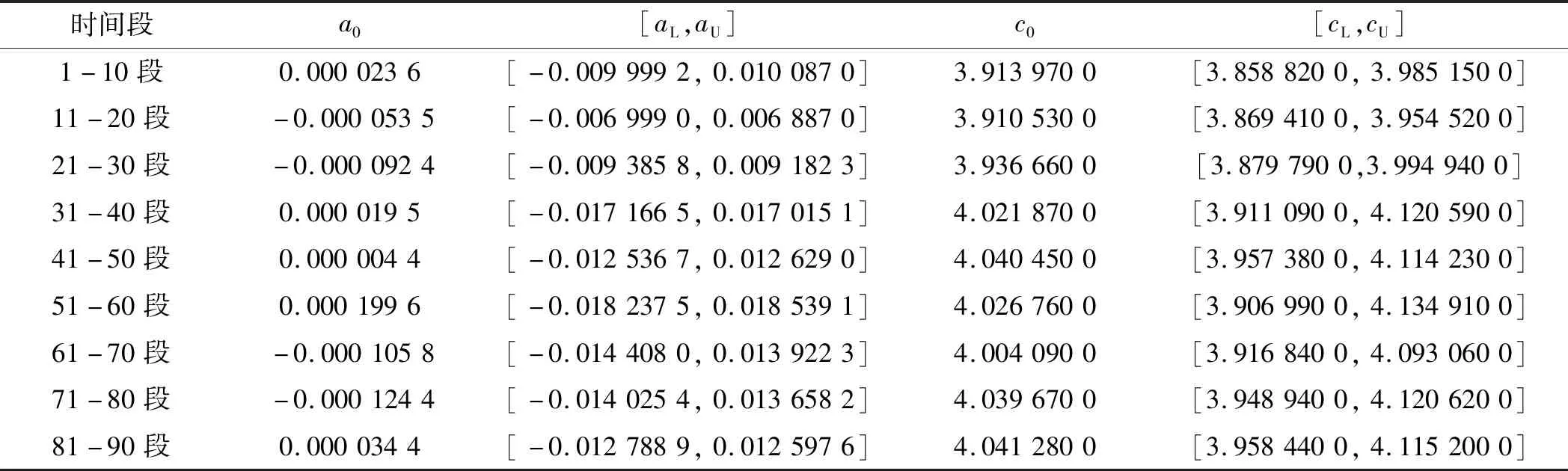
表3 时间序列XB的拟合系数

在各时间段内,时间序列XC的自助-最小二乘法拟合系数,如表4所示。

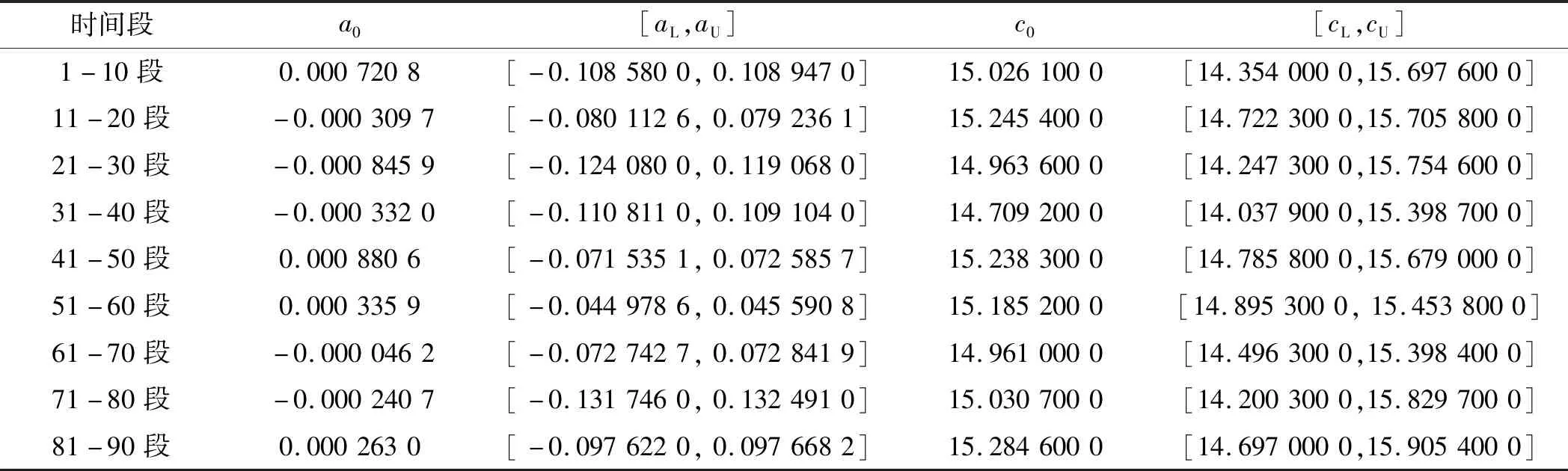
表4 时间序列XC的拟合系数

2.4 振动性能的动态预报

根据表(2～4),运用自助-最小二乘法线性拟合,可分别得到轴承各服役时间段,10个紧邻的振动性能的系数真值及上、下限;将其代入线性拟合方程,并设置自变量为11～20,可分别得到时间序列XA、XB、XC第11～20,第21～30,第31～40,…,等时间段振动性能的预报真值x0及上下限[xL,xU],即x0=a0×l+c0,xL=aL×l+cL,xU=aU×l+cU,其中:l=11,12,13,…,20。

上述过程反复运行,便可实现各个时间段振动性能的动态预报。

时间序列XA第11～100步的预报结果如图10所示。

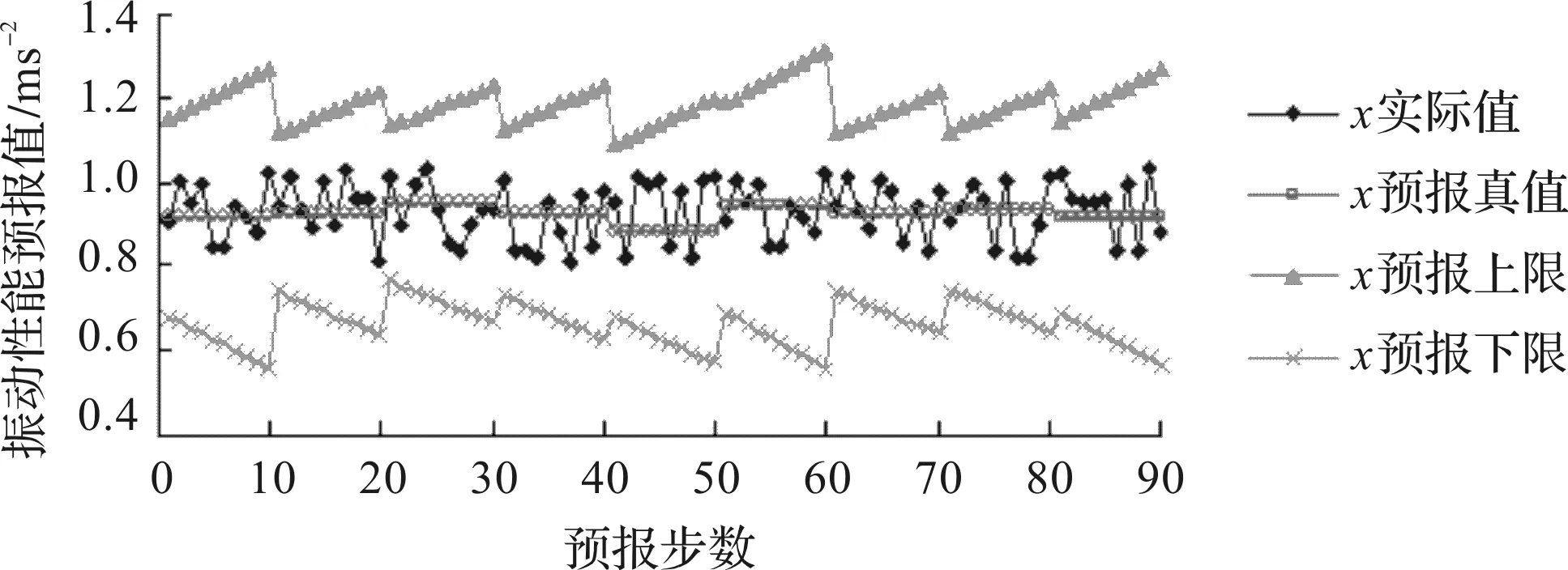
图10 时间序列XA各时间点振动性能的预报结果

由图10可得:时间序列XA各时间段振动性能的预报真值与实际值相差极小,第43次(即第53时间点)的预报真值与实际值相差最大,但仅为0.129 ms-2;振动性能的预报区间可将其实际值全部包罗,且上、下区间差值小,预报精度高。

以上结果表明,预报模型应用于轴承初期服役阶段的振动性能预报时是准确可行性的。

时间序列XB第11～100步的预报结果如图11所示。

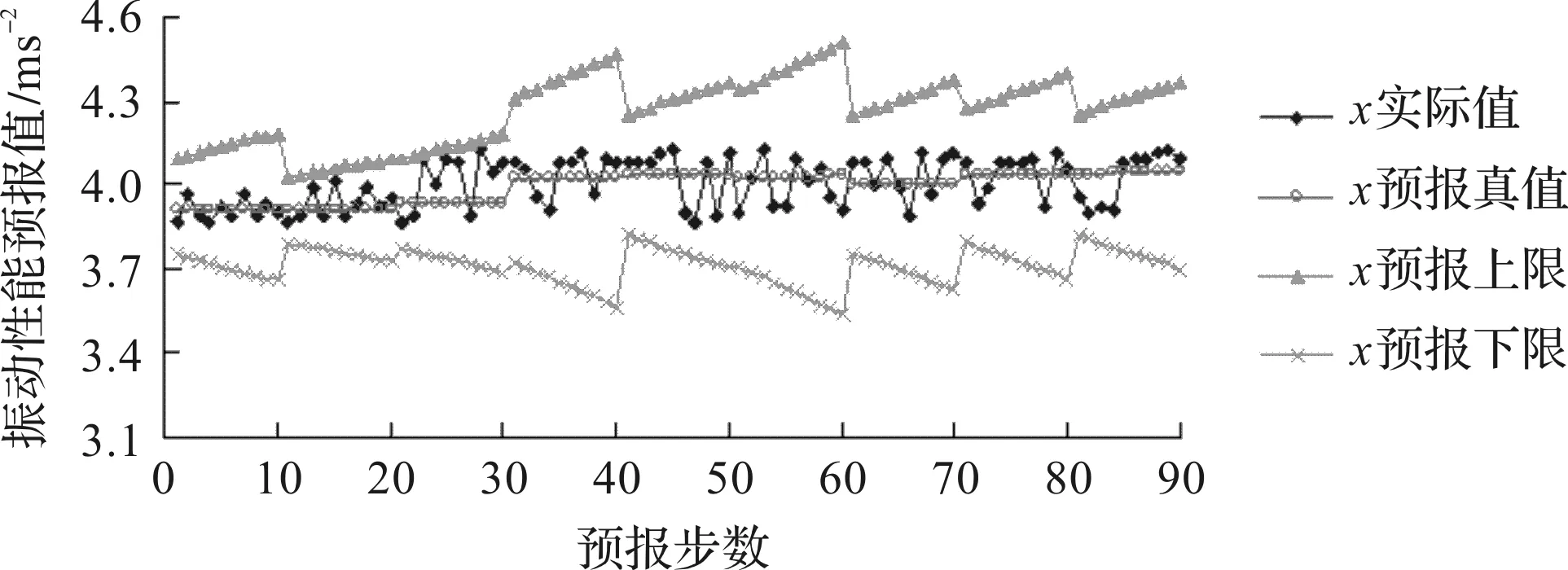
图11 时间序列XB各时间点振动性能的预报结果

由图11可得:时间序列XB各时间段振动性能的预报真值有逐渐上升的总趋势,与实际值的变化趋势保持良好的一致性;第28次(即第38时间点)的预报真值与实际值相差最大,但仅为0.188 ms-2;同样,振动性能的预报区间可将其实际值全部包罗,且上下区间差值小,预报精度高。

以上结果表明,预报模型应用于轴承中期服役阶段的振动性能预报时,同样是准确可行性的。

时间序列XC第11～100步的预报结果如图12所示。

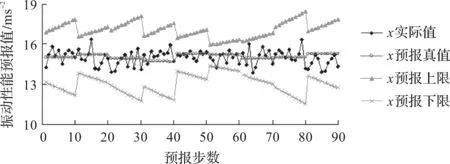
图12 时间序列XC各时间点振动性能的预报结果

由图12可得:时间序列XC各时间段振动性能的预报真值在实际值的均值附近波动,且波动范围极小;第85次(即第95时间点)的预报真值与实际值相差最大,但仅为1.379 ms-2;同样,振动性能的预报区间可将其实际值全部包罗,且上下区间差值小,预报精度高。

以上结果可以说明,预报模型应用于轴承临尾服役阶段的振动性能预报时,也是准确可行的。

为直观看出可靠度预报值与实际值的差异,笔者分别计算出时间序列XA、XB、XC预报真值与实际值之间的相对误差,其结果如图13所示。

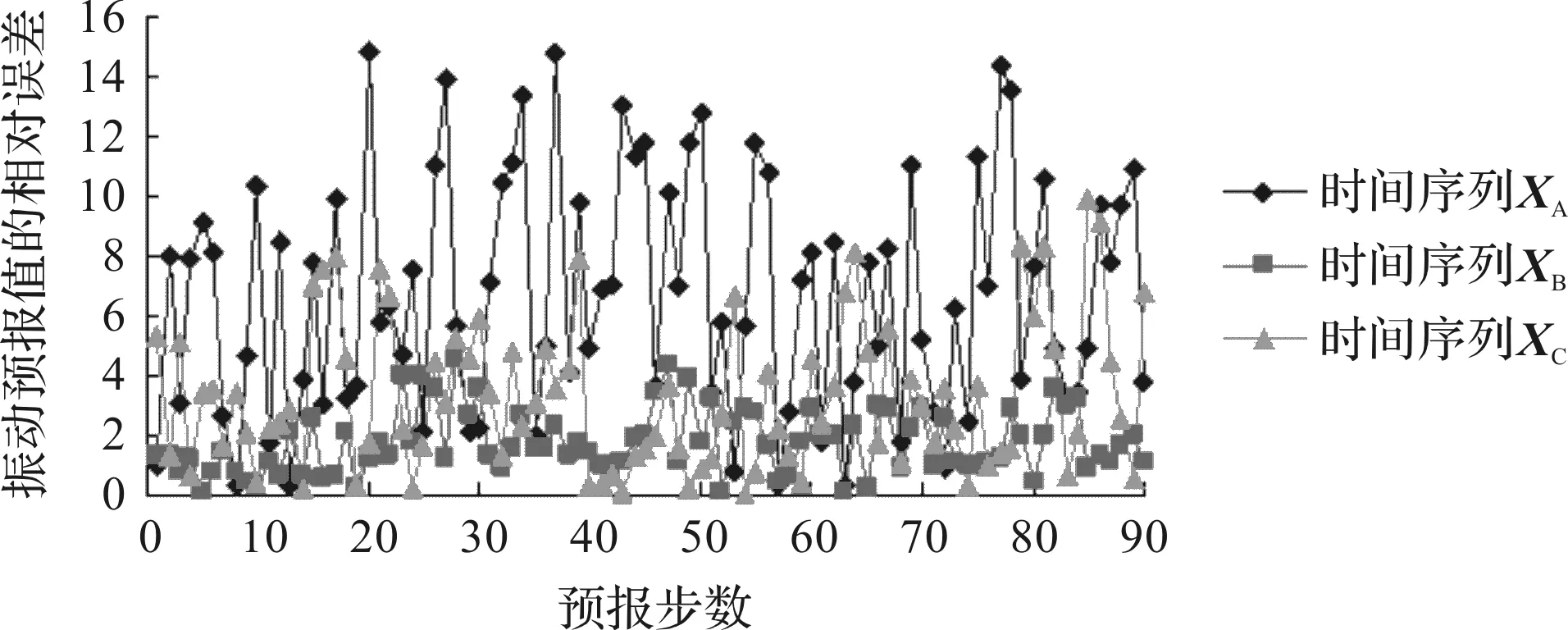
图13 可靠度预报值与实际值之间的相对误差

从图13可以看出:时间序列XA的最大相对误差出现在第37次(即第47时间点),但仅为14.73%;最小相对误差出现在第57次(即第67时间段),为0.29%;

时间序列XB的最大相对误差出现在第28次(第38时间段),但仅为4.57%;最小相对误差出现在第52次(第62时间段),为0.09%;

时间序列XC的最大相对误差出现在第85次(即第95时间段),但仅为9.91%;最小相对误差出现在第54次(第64时间段),为0.002%。

所以,振动性能预报值与实际值的相对误差较小,最大不超过15%,再次说明预测结果是十分真实可靠的,并可较好地应用于工程实际。

总体来看,初期服役时间序列XA的预报值与实际值差值最小,但相对误差最大,这是由于轴承服役初期振动小,即误差求取过程中分母基数低;中期服役时间序列XB的预报值与实际值差值较小,但相对误差最小,这是由于轴承服役中期振动较为稳定,预报值与实际值的上下波动小;

临尾服役时间序列XC的预报值与实际值差值最大,相对误差较小,这是由于轴承服役临尾振动较为剧烈,预报值与实际值的上下波动大,但误差求取过程中分母基数高。

基于时间序列XA、XB、XC的3个不同服役阶段试验案例的自助-最小二乘法线性拟合模型,可将紧邻且不断更新的10个振动性能值进行有效拟合;然后,根据最大熵原理将多个最小二乘解进行概率密度求取,在给定90%的置信水平下获得拟合解的最优估计和上下区间;最后,给定自变量并代入线性拟合方程,便可获得下一时间段振动信号的预报真值与区间上下限。

基于该模型得到的预报结果与实际值相对误差不超过15%,满足工程实际的预报要求;预报区间可将其实际值全部包罗,且上下区间差值小,预报精度高。

3个案例的振动性能预报值与实际值均保持良好的一致性,差值小、误差低、精度高,说明笔者所提出的模型具有良好的准确性及可靠性。此外,该模型不需考虑数据分布的任何信息,只针对现有数据做出最真实、客观的判断。该模型实现了对滚动轴承自我状况的在线监测。

3 结束语

为了对轴承振动性能序列进行动态预报,笔者将自助法与最小二乘法进行有效融合,提出了一种基于自助-最小二乘线性拟合的轴承振动性能序列动态预报模型。

首先,笔者对自助法与最小二乘法做了有效融合,对轴承振动时间序列进行了多次拟合;运用最大熵原理描述出拟合结果的概率密度函数,给定了相应的置信水平和时间变量,并不断地更替新旧数据,实现了滚动轴承振动性能的真值与区间的动态预报;通过3组实验数据验证了所提模型的准确性。

研究结果表明:

(1)自助-最小二乘线性拟合方法,可将振动时间序列多次拟合,有效反映出原始数据变化趋势的多个侧面信息;

(2)最大熵原理可准确描述出拟合结果的概率密度函数,快速求取拟合解的最优测度及上下区间;

(3)所提模型还可实现预报结果的自我验证,时间序列XA振动预报值与实际值的最大相对误差为14.73%;时间序列XB的最大相对误差仅为4.57%;时间序列XC的最大相对误差仅为9.91%;该预报结果满足工程实际的一般要求。

该预报模型可为后续滚动轴承自我健康检测以及在线故障诊断的研究提供理论根据;并可在工程实际中及时地发现问题,提前做好轴承早期失效的预防与监测工作。