矿用液力偶合器流场特性数值模拟及叶片数目优化*

王国强,崔红伟,2*,杨 敬,李 莉,李 健,任维微,黄 龙

(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.太原理工大学 煤矿综采装备山西省重点实验室,山西 太原 030024;3.霍州煤电集团 鑫钜煤机装备制造有限责任公司,山西 临汾 031400)

0 引 言

随着煤炭行业和综采技术的持续发展,重型机械设备不断投入使用,使采煤效率得到大幅提升。刮板输送机传动系统面临着难启动和超载等难题。而调速型液力偶合器由于其独特的工作原理能够有效地解决这些难题,大幅提升了煤矿设备使用的安全性[1]。

叶轮叶片数作为影响液力偶合器特性的主要因素之一,存在着合适的叶轮叶片数,可使偶合器的工作性能达到最佳。因此,探寻偶合器内流场的流场特性、转矩特性随叶轮叶片数的变化规律，及确定最优叶片数十分必要,有利于对偶合器的设计优化和选型[2,3]。

液力偶合器的传统设计主要依靠一维束流理论,基于经验公式和外特性试验进行设计。将流场三维流动简化为一维的方式难以准确反映偶合器内部流场随叶轮参数变化的规律,且最佳叶轮叶片数一般通过试验确定。由于一维束流理论在计算时进行了大量的假设与简化,使得计算结果的精确性无法保障,造成束流设计方法无法实现有效的叶片数目优化设计[4,5]。随着科学技术的发展和计算机性能的不断提升,计算流体力学在流体计算方面扮演了越来越重要的角色[6-10]。

国内外学者基于CFD技术对液力传动元件及相关参数进行了仿真研究和优化设计。国外学者HATAMI M等人[11]利用试验设计方法(design of experiments,DOE)中的中心复合设计对变几何涡轮叶片进行了优化设计。NAZANIN A等人[12]采用中心复合设计和遗传算法对离心式径向涡轮进行了优化设计,分析了设计参数的灵敏度,提高了峰值稳态效率。KIM S J等人[13]使用多元线性回归分析(multiple linear regression analysis,MLRA)对定子形状进行了优化设计,通过比较优化模型与初始模型的特性,评估了优化设计的有效性。LIU C等人[14]对液力变矩器进口偏角进行了参数分析及多目标优化,大幅缩短了变矩器设计周期。闫清东等人[15]通过搭建叶栅系统优化设计平台对设计变量进行了优化设计及试验研究,显著提高了缓速器的制动性能。卢秀泉等人[16]基于CFD数值模拟与试验研究了导轮关键参数对变矩器性能影响的规律。武琳琳等人[17]通过逆向建模与CFD结合的方式研究了液力变矩器工作轮叶片数对其原始特性的影响。罗冲等人[18]设计了一种新型液力缓速器,并利用CFD进行了仿真分析研究和台架试验验证,改进了传统缓速器结构和工艺复杂等问题。刘城等人[19]基于存档的小种群遗传算法对液力变矩器的叶栅参数进行了优化设计,有效地缩短了设计周期。刘春宝等人[20]基于CFD方法分别研究了液力缓速器结构参数对其性能的影响。魏巍等人[21]结合DOE试验设计、CFD与台架试验研究了液力变矩器叶轮厚度对变矩器性能的影响,在液力变矩器轻量化方面进行了探索研究。

以上研究主要集中于液力变矩器、缓速器等液力元件结构参数的优化设计,对于大功率矿用液力偶合器叶轮叶片数的设计所依据的理论局限于一维束流理论,缺少三维数值模拟优化设计研究。

笔者以CFD技术为基础,构建DOE及响应面模型(response surface methodology,RSM)对矿用液力偶合器叶轮叶片数进行优化设计,结合偶合器流场分布特性,分析额定转矩随叶轮叶片数的变化规律,为偶合器的优化改进提供可靠的参考。

1 数值模拟研究

1.1 计算模型

笔者以某型矿用调速型液力偶合器作为研究对象。由于该偶合器两对叶轮内腔结构完全相同,且空间呈对称分布,为了简化模型,笔者只选用其中一对叶轮作为研究模型。

该叶轮具体结构参数如表1所示。

表1 偶合器结构参数

笔者利用三维建模软件UG绘制了叶轮结构模型和包含流场的整体模型,通过求差获取了与叶轮模型互补的流场几何模型。

叶轮流场模型提取过程如图1所示。

图1 叶轮流场取出示意图

偶合器内流道为循环对称的结构,为了简化计算和提高仿真效率,笔者提取单个叶片对应的流场模型作为计算模型。

单流道模型提取过程如图2所示。

图2 单流道流场取出示意图

由于非结构化四面体网格能够实现复杂模型的快速划分,且保证流场数值模拟的稳定性和精确性,笔者在网格划分软件ICEM CFD中对不同叶片数对应的单流道模型进行四面体网格划分,且进行网格独立性检验。

具体检验结果如图3所示。

图3 网格独立性分析

由图3可得,随着全局网格尺寸的减小,仿真时长明显增大,且额定转矩逐渐收敛,当全局尺寸从2 mm变为1 mm时,仿真时长急剧增大,而额定转矩在较小的范围内变化,表明2 mm的全局尺寸已具备足够高的精度。

为了节省时间成本及提高仿真效率,笔者选取全局尺寸为2 mm的网格模型进行后续数值模拟。

流道网格模型如图4所示。

图4 单流道流场网格模型

1.2 控制方程

叶轮机械的叶栅绕流是典型的湍流现象,工作水液在泵轮叶片高速旋转带动下冲击涡轮,与叶片之间存在强烈的相互作用,偶合器内部为复杂的三维湍流流场。在额定工况工作过程中,偶合器通过循环换水使叶轮内流场温度维持在稳定的范围内,故温度的变化对液流流动特性影响较小,可以忽略。此时液流在流场内的流动受制于质量守恒方程和动量守恒方程[22-24]。

质量守恒方程是把质量守恒从物理学原理运用于流体力学中的流动模型推导出的流动控制方程,也被称为连续性方程,具体表达式如下:

(1)

式中:ρ—流体密度。

当工作介质可视为不可压流体时,ρ为常数,此时上式可简化为:

(2)

动量守恒方程,是把牛顿第二定律运用于流体力学中的流动模型推导出的方程,也被称为Navier-Stokes方程。

该方程的张量形式可表示为:

(3)

式中:δij—克罗内克尔(Kronecker)符号;fi—体积力。

对于动力黏度为常量的不可压流体,上式可简化为:

(4)

1.3 仿真计算条件

1.3.1 边界条件

由于采用单流道流场模型进行数值求解,笔者将流场循环切割面设置为周期性边界循环;对叶轮流场交界面处通过采用流体力学仿真软件CFX中的Stage(Mixing-Plane)方法进行了求解,通过在交界面处建立混合平面进行了定常计算,实现了利用定常计算方法解决非定常问题;其余壁面均设置为无滑移边界条件;湍流模型采用能够精确预测流动和分离的剪切应力传输模型(shear stress transport,SST);收敛判定准则设置迭代的残差值为小于10-5。

参考偶合器实际工况与数值计算要求,笔者做了以下假设:

(1)在实际工作中,液力偶合器通过循环换水实现散热,故忽略温度变化引起的能量损耗;

(2)工作水液为不可压缩黏性流体且不考虑叶轮的水液泄漏;

(3)偶合器在工作过程中不发生变形和轴向移动。

1.3.2 工况条件

为了分析偶合器额定工况条件下转矩随叶轮叶片数的变化规律,笔者根据偶合器实际工作状态设置额定工况点速比为i=nT/nP=0.945,泵轮转速nP为1 480 r/min,涡轮转速nT为1 398.6 r/min,选取全充液工况进行数值模拟计算。

2 叶片数优化设计

2.1 DOE试验设计

笔者将全充液额定工况仿真计算得到的额定转矩值设为优化目标,泵轮叶片数zP、涡轮叶片数zT为试验因素,取值范围分别为24～57、27～60。若进行全因子设计,需完成342=1 156次参数建模、网格划分及仿真计算。由于进行数值模拟计算会耗费大量的时间并占用计算机大部分存储空间,故全因子设计不可行。

此处试验设计方法采用最优拉丁超立方设计,该方法能够真实地拟合因子与响应,保证试验点的均匀分布和空间填充。试验设计中泵轮叶片数和涡轮叶片数皆为12水平。

具体数据如表2所示。

表2 最优拉丁超立方设计表

2.2 RSM优化设计

笔者对表2中叶轮叶片数组合对应的单流道模型重新进行网格划分和数值模拟计算,将得到的额定转矩值作为近似模型的样本数据,并采用RSM模型拟合样本数据,该近似模型通过建立多项式函数来确立复杂的响应关系[25]。

为了提高响应面模型可信度和预测精度,笔者新增了24组数据作为样本数据,对得到的样本数据进行一阶到四阶的响应面模型拟合,且随机选取10个样本计算模型近似误差,并通过各项目标验证模型的效果。

笔者采用Isight软件中的自适应模拟退火算法对建立好的响应面模型进行了寻优,优化目标为液力偶合器额定转矩值最大。

由于响应面方法用代数表达式表现因子与响应之间的关系,造成少数的样本点不在响应面上,模型存在一定的误差。故笔者取zT=36、37、38、39、40和zP=32、33、34、35、36交叉组合共25组进行CFD仿真计算,验证响应面模型的精确性。

3 结果分析

3.1 叶片数敏感性分析

笔者通过对最优拉丁超立方设计结果进行拟合,得到主效应图、交互效应图、parteo图。

叶轮叶片数对偶合器额定转矩影响的parteo图如图5所示。

Parteo图表示样本拟合后模型中每一项对响应的贡献值,Te为贡献的具体值,正值为正效应,表示随着对应指标的增大,偶合器额定转矩值也随之增大,负值与之相反。从图5中能够明显看出,叶片数二次项对额定转矩的作用最大。

叶轮叶片数对额定转矩的主效应如图6所示。

图6 叶轮叶片数对额定转矩影响的主效应图

由图6可得,随着叶片数的增加,额定转矩呈现先增大后减小的变化趋势,且涡轮叶片数和泵轮叶片数存在明显的最优值。

通过上述分析可知,涡轮叶片数和泵轮叶片数对额定转矩皆呈较强的二次相关关系,图形为开口向下的抛物线形状,涡轮和泵轮叶片数对额定转矩具有相同的影响效果,且二者的相互作用对额定转矩有较强影响。

叶轮叶片数对额定转矩的交互效应如图7所示。

图7 叶轮叶片数间交互效应图

从图7中可以看出,两条线明显相交,表明对偶合器额定转矩而言,涡轮叶片数与泵轮叶片数之间有显著的交互效应。

3.2 优化结果分析

笔者通过建立RSM模型,得到满足误差许用要求的三阶和四阶拟合模型。相较于四阶拟合模型,三阶拟合模型平均误差、最大误差、均方根误差值更小,同时R2拟合度值更大,对数据的拟合度更好,因此笔者采用三阶响应面模型对液力偶合器额定转矩与叶轮叶片数进行了拟合。

偶合器额定转矩与叶轮叶片数间的关系如图8所示。

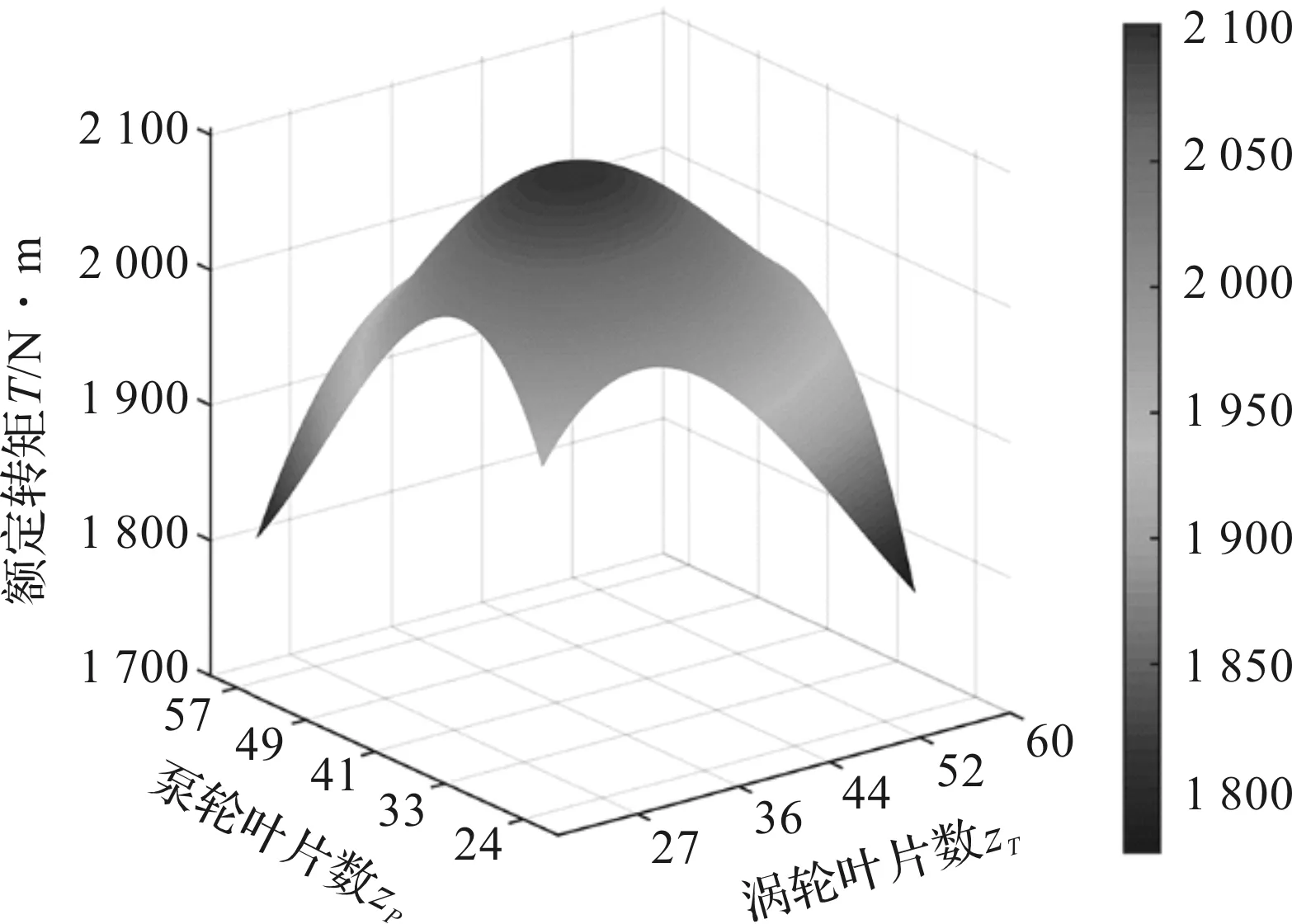
图8 RSM响应面近似模型三维曲面图

从图8中可以看出,额定转矩存在明显的波峰,证明叶轮存在最佳叶片数使得额定转矩值最大。通过Isight中的自适应模拟退火寻优得到叶轮叶片数最优解为:zT=38,zP=34,T=2 106.4。CFD验证得到的最优解为:zT=37,zP=34,T=2 126。

CFD仿真验算结果与RSM优化结果相差极小,涡轮叶片数相差1片,转矩值仅仅相差0.93%,验证了响应面近似模型具有很高的精度。

3.3 流场分布特性分析

为了研究偶合器叶轮叶片数内流场特性和转矩特性分布规律,参考优化后的叶轮叶片数,笔者设计了7组叶轮叶片数组合,具体方案如表3所示。

表3 叶轮叶片数方案设定

笔者选取了方案1、方案4、方案7这3种典型叶片数组合,对偶合器内流场特性影响规律进行分析研究。

叶轮叶片压力分布云图如图9所示。

由图9(a～c)可得,额定工况下叶轮间的转速差较小,液流在流动过程中各种能量损失相对较低,离心力成为压力改变的主要因素。由于循环圆外环处液流在流动过程受到离心力的作用最大,且经过泵轮加速之后液流速度较高,造成的冲击力较强,在循环圆外环处的压力值最大,颜色接近于色谱中的红色。

从图9中可以看出,3组方案整体压力分布趋势相同,沿循环圆外径向着内径逐渐减小。而方案4最大压力值小于其他方案,且最大压力值区域要明显小于其他方案,负压区域显著大于其他两种方案,压差最小。

图9 涡泵轮叶片压力分布云图

叶轮流场速度流线分布云图如图10所示。

由图10(a～c)可得,经泵轮加速的液流冲击涡轮叶片导致液流速度降低,在叶片之间的中心区域即循环圆中心区域形成了漩涡现象。随着叶片数的增加,液流流速呈现先增大后减小的趋势,液流流动由不稳定向稳定，再向不稳定转变;

图10 涡泵轮流场速度流线分布云图

方案1由于泵轮叶片数目太少,液流在泵轮的作用下得不到有效的加速,使得液流速度低,且流线呈现不稳定的状态;方案4流动最稳定,漩涡最集中;方案7由于叶轮叶片数太多,降低了叶轮有效容腔,液流在流动过程中损失增加,所以液流速度呈现下降的趋势,

且漩涡范围开始扩大。

3.4 额定转矩特性分析

笔者选取表3中的方案1～7对偶合器转矩特性进行分析,得到了偶合器额定转矩随叶轮叶片数变化规律图,如图11所示。

图11 额定转矩随叶片数变化趋势

由图11可得,随着叶轮叶片数的增加,偶合器的额定转矩呈现先增大后减小的趋势,方案4的额定转矩值最大,且方案3到方案5额定转矩值变化趋势较为缓和。

通过对叶轮流场特性分析可知,当叶片数较少时,增大了液流出口偏离角度,造成流动循环转换不充分且液流冲击和容积损失增大,表现为液流流动不稳定、形成的漩涡不集中、液流流速慢等,造成传递力矩的能力下降,即偶合器的额定转矩值变小;而叶片数太多时,单个叶片对应的流场体积减小,降低了叶片的有效容积,减小了过流面积,增大了液力损失,使得流体传递的转矩降低。

为了说明涡轮和泵轮叶片数单独变化时对偶合器额定转矩的影响,笔者以优化设计得到的涡泵轮叶片数为基准进行分析。

设计方案如表4所示。

表4 单个叶轮叶片数变化时方案设定

额定转矩随单个叶轮叶数变化规律如图12所示。

图12 额定转矩随单个叶轮叶片数变化规律

由图12可得,偶合器叶轮叶片数单独变化对额定转矩的影响规律与叶轮数整体变化时大致相同。与之不同的是即使单个叶轮的叶片数处在最优时,与之匹配的叶轮叶片数太少或太多也会严重影响偶合器的性能,使偶合器的额定转矩值大幅降低;

图12(a)中,涡轮叶片数为最佳叶片数37,泵轮叶片数由21变为24时,转矩值有明显的提升,泵轮叶片数在29～45变化时,偶合器的额定转矩变化范围很小,额定转矩曲线变化趋势相对缓和;

与图12(a)相比,图12(b)中泵轮叶片数为最佳叶片数34时,额定转矩随涡轮叶片数整体变化趋势较为缓和,且涡轮叶片数为32～48时,额定转矩变化范围很小。

结合前面CFD仿真验证时得到的25组叶片数组合分析可知,当涡泵轮叶片数相差1～3片时,偶合器的额定转矩值变化极小,可忽略不计。

4 结束语

笔者结合计算流体动力学软件CFX与Isight软件对叶轮叶片数进行设计与计算,并对额定工况条件下偶合器内流场特性及转矩特性进行了分析研究。

研究结论如下:

(1)通过对偶合器不同叶轮叶片数的流场分布特性和转矩特性对比分析得出:偶合器叶轮叶片数存在明显的最优值使得偶合器性能最佳,叶轮最优叶片数会使偶合器在实际工作过程中获得最佳有效容腔,表现为液力损失降到最低,循环流量转换充分,从而传递转矩的能力增强;当涡泵轮叶片数相差1～3片时，偶合器的额定转矩值相差不到0.5%,液力偶合器的性能差别极小。叶轮叶片数对偶合器特性分布影响具有一定规律,解释了叶轮叶片数造成偶合器性能差异的内部原理,为偶合器叶轮叶片数研究提供了可靠的数据基础;

(2)以CFD技术为基础,笔者利用DOE试验设计和响应面(RSM)模型进行了叶轮叶片数的设计,采用Isight软件中的自适应模拟退火算法进行了响应面寻优,并直接进行了仿真验证,结果表明:恰当的DOE试验设计与响应面模型能够在相对较短的时间内精确地预测叶轮叶片数对偶合器额定转矩的影响规律,快速确定液力偶合器叶轮最优叶片数,为今后偶合器的设计优化及选型提供了可靠的理论支撑。

在后续的研究中,笔者将搭建偶合器转矩特性试验台架,通过测定最优叶片数的额定转矩,验证偶合器叶片数优化方法的准确性和效果。