浅谈高等代数在几何中的应用

黄 昊

（西昌学院）

一、高等代数与几何学之间的关联

高等代数与几何学有诸多相似之处，高等代数中的某些理论就是从几何学中发展而来，高等代数与几何的发展可谓是相互联系、相互促进的，两者相辅相成，几何以更加直观的形象将高等代数所表达的含义呈现出来，而高等代数为几何提供了有效的研究方法。如几何学中的向量共线、共面的充要条件可以运用高等代数中行列式工具来表达；两门课程看似不相关，其实他们之间有着莫大的关联，几何学中一维、二维、三维空间与线性代数中的n纬空间相对应，反之从线性代数的观点来看，线性空间的诸多理论源自几何学一、二、三维空间的推广；如此看来，我们在研究几何学时，可以运用“高等代数”为工具进行解析，尤其是高中阶段的几何学习过程中，可实现二者的有效结合，利于教学的有效开展，能够帮助学生更好地认识几何知识，同时更早的接触高等代数，为后期的学习打下基础。

二、高等代数在几何学中应用的研究目的

高等代数是大学重要课程之一，当前的高等数学是经过很多科学家不断改进完善的结果，如今高等数学成为很多学科的基础课程，诸如科研、工程设计、物理学或化学研究等等都需要高等代数为基础。而几何这门学科由来已久，但因该学科的特殊性，很少人能够真正领悟几何学真正的内涵。若能够将高等代数与几何联系起来，发挥各自优势，会为几何学的发展带来积极的影响。

关于高等代数与几何学关联的研究，著名的法国数学家约瑟夫·拉格朗日表示：假若代数与几何独立分开发展，那两者的发展速度将会非常缓慢，其应用的范围也比较窄，但如果能将两者结合起来研究，那高等代数与几何学的发展将会突飞猛进，应用范围也大大拓宽。当下我国有不少知名大学将高等代数与几何学进行合并，如同济大学、兰州大学等等，其教学效果相比未合并前有了显著的提高。

三、高等代数在几何学中应用

（一）高等代数“行列式”与几何“向量”之间的关系

图1 向量示意图

（2）行列式与向量之间的关联：

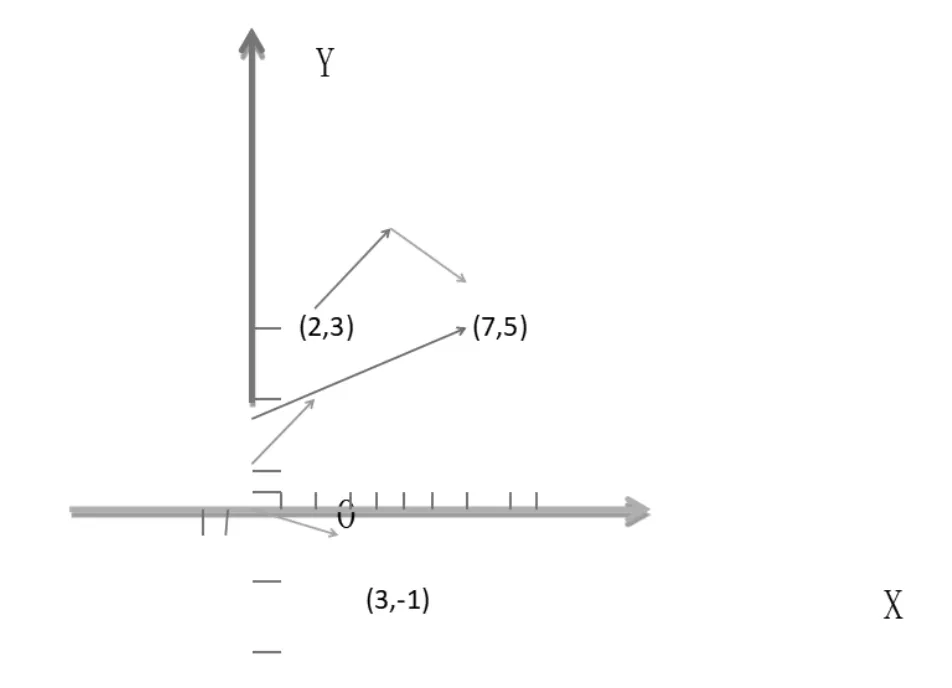
图2 向量二维关系图示

以上是2元一次方程所对应的几何中的平面中向量的关系，2元方程对应的是2维度，那以此类推，三元一次方程对应的是几何中的三维概念，n个线性方程组多对应的就是n维空间的向量关系。

（二）线性方程组与平面对应关系

众所周知，两个平面在空间中的关系为相交、平行、重合三种关系，如图3所示（平面重合不再赘述）：

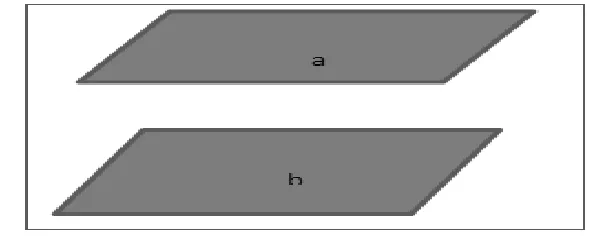
图3 平面a//平面b

图4 平面a相交于平面b

从高等代数的角度来验证两平面的关系：

若平面a与平面b平行，则充要条件为：

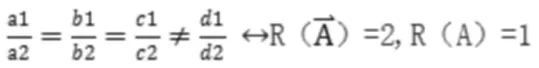
若平面a与平面b重合，则充要条件为：

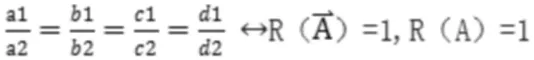
若平面a与平面b相交，则充要条件为：

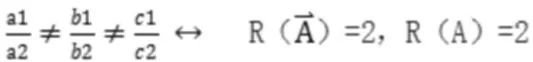
证明：

若平面a与平面b平行，则两个平面没有交集，无公共点存在，

同理可证明面a与平面b重合、平面a与平面b相交的充要条件成立。

（三）线性方程组在直线位置关系判定中的应用

两条直线在空间中的关系有四种，分别为重合、平行、异面与相交。

我们先定义两条直线的线性方程，通过方程组的形式来讨论直线之间的几种对应关系。

直线1方程：记为m1：

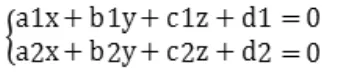
直线2方程：记为m2：

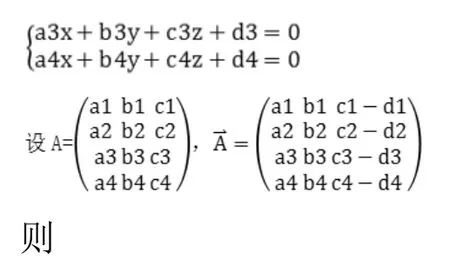
证明：

线性方程组为：

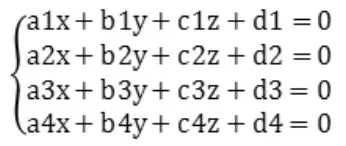
四、结语

几何是基础教育中数学学科的重要组成部分，几何与高等代数有着密切关联，中学阶段学生在学习几何过程中比较吃力，抽象的几何知识让不少学生望而却步，不知该如何应对，本文简要探讨了高等代数在几何学中应用，为培养学生数学思维、提升学生几何学习效果起到了一定的效果。在素质教育背景下，中学数学老师应积极探索高等代数在几何中的应用策略，为学生打开学习几何的新局面。当然，当下高等代数在几何中的应用并不完善，需要不断改进、完善，更深层次地探索两者的关联，更好地实现高等代数在几何学中应用。

【相关链接】

西昌学院坐落在四川省西昌市，是经教育部备案的全日制普通本科学校，是四川省、教育部、国家民族事务委员会共建高校，国家教育现代化推进工程应用型本科高校建设项目学校、四川省“本科院校整体转型发展改革”试点单位；入选国家“卓越农林人才教育培养计划”“四川省卓越农林人才教育培养计划”“四川省卓越工程师教育培养计划”、“四川省卓越教师教育培养计划”。

学院肇始于1939年北洋工学院内迁西昌创建的国立西康技艺专科学校。2003年经教育部批准由西昌农业高等专科学校、西昌师范高等专科学校、凉山大学、凉山教育学院合并组建为省属全日制普通本科院校。