稀疏参考点下的室内定位方法

2022-06-23 02:45郭学斌李长庚高山流水

信号处理 2022年5期

郭学斌李长庚高山流水

（中南大学物理与电子学院，湖南长沙 410083）

1 引言

随着智能手机、Wi-Fi 和蜂窝网络的迅速发展，室内定位技术在购物导航、应急救援、物流仓库和生产安全等诸多领域有广泛应用，基于位置的服务是打通线上与线下的关键点［1］。由于室内环境复杂，加上墙壁的阻隔，卫星定位在室内的定位精度较低，无法满足人们的需求。随着商场、医院、图书馆等大型室内场所越来越多，利用现有的设备如Wi-Fi 进行定位的方法因成本低、精度高成为研究的热点［2］。

传统基于Wi-Fi 的定位算法在信号采集阶段费时费力，构建的指纹数据库难以保证精度，所以越来越多的人使用信道损耗模型、空间插值等算法来得到更多的参考点（Reference point，RP）。Narzul⁃laev 利用接收机收到的电磁波的接收信号强度值（Received Signal Strength Indicator，RSSI）与发射机、接收机之间的距离的经验损耗模型，提出了一种基于斜坡模型的估计算法［3-4］，来估计无线接入点（Access Points，AP）附近不同位置处的RSSI 值，此算法平均定位误差达到3.6 m。Ding 等人提出了一种区域传播模型，因为障碍物阻挡、多径效应等因素会引起信号的衰减，所以通过人工划分区域来进行指纹的估测，不过缺乏理论证明，也增加了人力成本［5］。Talvitie 对不同插值算法最近邻法、梯度法、反距离加权法进行了比较分析，实验表明反距离加权法（Inverse Distance Weight，IDW）的性能较好，平均定位误差在4 m 左右［6］。相比较于以上插值算法，克里金插值算法（Kriging Interpolation，Krig⁃ing）不但考虑了待插值点的位置与RP 位置的相互关系，还充分考虑了区域化变量的空间相关性。Jan使用克里金插值算法得出的定位误差约3 m，与未插值相比精度提高了18%［7］，但仍无法满足定位需求。因Wi-Fi信号不稳定，易出现噪声和离群点，所以在构建指纹数据库时需要长期监测并进行滤波，传统滤波算法如高斯滤波、均值滤波结构简单且无法对缺失点进行判断。为防止数据库冗余导致资源浪费，需对AP 的位置表现能力进行筛选。现如今已有的AP 筛选方法包括基于RSSI 最大均值的AP 选择算法（Max Mean，MM）、随机AP 选择算法和基于RSSI 均值最大累计差分（Max Cumulative Dif⁃ference，MCD）的AP 筛选算法［8］等。MM 算法不能体现AP 在不同RP 信号强度差异。随机AP 选择算法具有很强的随机性，不具有普适性。MCD 虽然可以选出位置表现能力较强的AP，但对缩小数据库的能力有限。

本文一是对插值精度较高的克里金进行了改进，提出使用支持向量回归算法（support vector re⁃gression，SVR）对克里金插值的变异函数进行拟合，该算法克服了原有的主观选取拟合模型的不灵活性，提高了拟合精度，降低了信号采集的工作量。二是对卡尔曼滤波算法加入了缺失点判定，不仅对信号噪声进行了抑制，对缺失点也可以有效地识别并消除。此外，庞大的数据库导致运算量成倍增加，但部分AP 位置区分度不高，造成资源的浪费，因此本文提出基于信号强度差分方差（Cumulative Difference Variance，CDV）的AP 筛选策略，求出各AP 点在不同位置RSSI 值的差分方差，找出具有最小差分方差的AP 点并滤除，实验表明该算法能够在保证定位精度的同时缩小指纹库的规模，大大节约了资源。将本文方法与其他文献进行对比，在二维定位中，文献［9］提出了一种基于差分信号强度和动态线性插值的鲁棒定位指纹算法，其平均定位误差在1.50 m 左右，文献［10］提出一种基于分区确定和曲面拟合的室内定位方法，其平均定位误差2.05 m左右，本文定位方法得到的1.01 m精度具有一定的优越性；在三维定位中，文献［11］提出了一种基于服务器、遗传算法优化的级联人工神经网络定位模型，平均定位误差在1.90 m 左右，文献［12］采用自适应扩展卡尔曼滤波估计行人的实时航向和行走速度，结合Wi-Fi 接收到的信号强度指示和往返时间进行近距离检测，平均定位误差在1.14 m左右，相比之下本文定位方法0.92 m 的精度表现较好。

2 传统室内定位方法

室内定位技术多种多样，如惯性传感器室内定位技术、基于Wi-Fi 的室内定位技术、地磁定位技术、基于计算机视觉的定位技术和光跟踪室内定位技术等等。基于Wi-Fi的定位技术因不需要额外布置硬件且精度较高成为主流。通过Wi-Fi进行的室内定位主要分为指纹库定位法和几何测量法。几何测量法需要高精度的测量设备，且受多径效应影响较大［13］，指纹库定位算法不需要测量距离进行定位，主要是通过比较待测节点与参考节点之间RSSI值的相似度进行位置估算，得到待测节点的坐标信息，而被广泛应用，指纹库定位算法具体步骤如图1所示。

离线阶段主要是采集数据构建指纹数据库。指纹数据库包括不同的参考节点处测量到的来自不同AP的信号强度值与坐标信息。测量过程中并不需要知道AP 节点的位置信息。所以信号噪声、AP 可靠性、参考点数量成为指纹库性能的重要指标。

在线阶段即指纹匹配阶段，通过待测点的指纹信息与指纹库匹配得到定位结果。目前主流的方法就是WKNN 算法［14］，WKNN 算法如公式（1）所示，假设有m个RP，l个AP，Sk表示测试点（Test point，TP）接收到的第k个AP 发送的信号强度，fik表示在指纹数据库中第i个RP 接收到的第k个AP 的信号强度。q=1 时，di为曼哈顿距离，q=2 时，di为欧氏距离。蔡敏敏通过实验发现信号强度越大的AP 对定位误差的影响越大，所以赋予信号好的AP 以较大的权重，更加符合实际，故在WKNN 的基础上设计了AWKNN 算法［15］，第k个AP 的权重值wk用第k个AP的信号强度值与该点所有AP信号强度和的比值来表示，如式（2）所示，欧氏距离如式（3）所示。

最后选取距离最小的n个点，求加权平均就可以得到最终的匹配结果。如式（4）所示，(xi，yi)用来表示第i个RP的坐标，(x，y)表示最终的匹配结果。

3 指纹库构建算法设计

3.1 改进的卡尔曼滤波算法

Wi-Fi 信号在室内环境中传播时，受多径传播、非视距传播等多种因素的影响，会产生波动，最终降低定位精度，所以需要采集多组数据，并进行滤波。由奥地利数学家Rudolf Emil Kalman 提出的卡尔曼滤波是一种时域、高效率自回归滤波方法［16］，适用于线性系统。卡尔曼滤波用状态方程描述输入输出关系，以“预测-观测-修正”为基本思想，通过系统观测数据对系统状态进行最优估计［17］。目前，该方法已经应用在惯性导航、目标定位、传感器数据融合、人脸识别等多个领域。该系统的状态方程如式（5）所示。

其中，x(k)表示系统在k时刻的状态，u(k)表示控制量，w(k)表示符合高斯分布的过程噪声，A和B为系统参数，因Wi-Fi 信号为单输入单输出，所以A、B为常数。系统的观测方程如式（6）所示。

其中z(k)表示系统在k时刻的观测值，y(k)表示符合高斯分布的测量噪声，H是系统参数。在工程中用卡尔曼滤波是迭代的过程，每获得一个新观测值就迭代一次，来回更新系统状态x和误差协方差P，每一次迭代分为预测和修正两个步骤。预测是指根据前一时刻迭代的结果x(k-1|k-1)和P(k-1|k-1)来预测这一时刻的系统状态x(k|k-1)和误差协方差P(k|k-1)。系统的预测方程组如式（7）、（8）所示。

其中R为符合高斯分布的测量噪声。在一些简单的场景中，上述方程可以简化。例如在测量温度、加速度、Wi-Fi信号强度时，是没有控制量的，即B为0，且A和H也可取为1。因此预测方程组和修正方程组可以进行简化，通过化简和并，可将整个卡尔曼滤波过程用三个式子迭代来表示，如式（12）、（13）、（14）所示。

信号采集中将无法采集到的信号标记为0，这会大大降低卡尔曼滤波的性能，本文对卡尔曼滤波算法进行改进，在卡尔曼滤波中加入缺失点判定，并将信号缺失的时间节点去除，对剩余数据进行滤波，这样就可以同时抑制离群值和缺失点对信号的干扰，最后使用均值计算得出该点用于定位的信号强度。具体步骤可以表示为图2所示。

3.2 基于CDV的无线接入点筛选策略

MCD 筛选算法是选择AP 在不同RP 上RSSI 差值之和来衡量AP 信息量，若AP 在不同RP 点之间的差异越大，表明该AP 具有更强的位置表现能力。文献［18］提出无线信号在不同AP 上的空间分布是不同的，部分AP 的无线信号空间差异明显，反之不明显，选择RSSI值的方差来描述AP的空间区分度，此方差即信号强度的离散程度可用来表示AP 提供的位置信息的数量，实验表明用方差来判定信息量在保证定位精度的同时指纹数据库减少了42.64%。基于上述内容本文提出一种基于差分方差的AP 筛选算法（Cumulative Difference Variance，CDV），CDV 筛选算法是根据AP 在不同RP 处信号强度的差分方差来描述AP 对位置信息的敏感度，差分方差表示不同RP 点RSSI 差值的离散程度，信息量更多，数据更加精细，更有利于对AP在不同RP点的差异性进行判断。设在实验区域中有M个AP和N个RP，RSSIi，j表示无线接入点APj在第i个RP处的RSSI 值，第i个RP 与第k个RP 间的信号差分是APj在两个RP 上的RSSI 差异，如式（15）所示。APj信号在不同RP 处信号强度的差分方差σVCDj2如式（16）所示。

其中diff0表示两两RP 之间RSSI 差异的平均值，σCDVj2表示APj在不同RP 处信号强度差异的离散程度，可较好的表征不同RP 处RSSI 的差异。通过式（12）计算出每个AP 的差分方差后，选定一个合适的阈值，将差分方差小于阈值的AP 筛除，保留差分方差较大的AP用于后续的匹配定位。

3.3 基于支持向量回归拟合的克里金插值法

克里金插值是地质统计学的核心，一种空间估计技术。与传统的插值方法相比，克里金插值法在数据网格化的过程中，考虑到了描述对象的空间相关性［19］，插值结果更能真实的表示实际情况。克里金插值算法的假设是同一个AP节点的RSSI值是空间相关的，离参考节点越近的节点，其对应AP 的RSSI 值越相似。克里金插值算法的主要思想是使用已知的测量数据来制定一个半方差函数［20］，用于在未观察到的位置产生具有最小误差方差的无偏估计。半方差是克里金插值中的一个重要概念，它描述了参考节点之间的空间相关性。第i个RP 和第j个RP 之间的理论半方差γij定义如式（17）所示。其中，z(ui)表示RP点ui的所有RSSI 值。实验中的半方差γ(h)定义如式（18）所示。其中，h表示的是参考节点ui和uj之间的距离；N(h)是间隔为h的RP点的数量。

根据公式（18），可以绘制出实验半方差函数图。将绘制出的图形与理论半方差函数进行拟合，得到最接近的函数模型。常见的半方差函数模型有球面模型、指数模型和高斯模型等。具体形式如式（19）、（20）、（21）所示。其中，E表示的是半方差趋于恒定时的临界值，A值称为临界距离，表示的是在这个距离范围内，半方差函数随着距离的增加而增加，超过这个距离，半方差趋于恒定。根据拟合的半方差函数模型，可以得到具体的参数，如图3（a）所示。但根据经验选取传统半方差函数模型往往不够灵活，拟合效果不好，存在较大误差。部分文献采用多次实验选取效果较好的函数模型，但效果不理想并且算法复杂度较高。本文采用支持向量回归的方式对半方差函数进行拟合［21］，如式（22）所示。其中G为正则化常数，lε为不敏感损失函数，w和b是待确定的模型参数，γ为半方差函数值，通过支持向量回归训练就可以得到最终的γ(h)［22］。算法示意图如图3（b）所示。

4 室内定位方法实验

4.1 实验场景

选取了中南大学物理楼4 楼、5 楼、6 楼进行实验。本文在两个区域采集数据，区域A 为6 楼的全部区域即二维，如图4 所示，共61 个RP，随机选取100 个TP，RP 点采样间隔为2.4 m。区域B 为三层楼的矩形区域即三维区域，如图4 中的矩形区域所示，各楼层布局相同，共36 个RP 点，随机采集69个TP，RP 点采样间隔为2.4 m。本次共实地采集到455 个AP，因AP 分布在三维空间任意位置故并未标出所有AP点的位置。

4.2 离线阶段构建指纹数据库

对于Wi-Fi 的RSSI 数据，使用专门设计的采集软件“指纹地图”进行采集。Wi-Fi 发射机主要为TP-LINK，型号为TL-WR886N，其拥有3 根2.4G 天线，最高无线速率450 Mbps，以及TL-WDR5620，其拥有2 根2.4 GHz 天线、2 根5 GHz 天线，最高无线速率867 Mbps。Wi-Fi 接收机型号为华为P30 智能手机。在长达三个月内，选取早、中、晚不同的时间段在RP点和TP点上采集多组数据。将采集到的数据实时导入到电脑上，使用matlab 进行提取并分析，信号采集界面如图5 所示。该软件可以设置频率、时长进行采集-100 dBm 到0 dBm 之间的信号，并将数据实时传送到电脑端。

对同一RP 多次采集的信号强度使用改进的卡尔曼滤波进行处理，得出最终的信号强度值，然后使用CDV筛选算法过滤掉信息量较低的AP点，得到初始的指纹数据库。再选用不同插值算法对指纹数据库进行插值估计，得到重构后的指纹数据库。

4.3 在线定位

采集测试点，使用AWKNN 算法匹配出最终的位置。

5 实验结果及分析

5.1 指纹库构建算法性能分析

5.1.1 改进卡尔曼滤波性能分析

将同一段信号用不同滤波算法进行处理，如图6所示，改进卡尔曼滤波不仅可以有效地抑制噪声，对缺失点的处理也更加准确。在定位区域内，分别使用改进的卡尔曼滤波、卡尔曼滤波以及不做处理三种方式得到的RSSI 进行定位，定位方法采用AWKNN，最终得到的定位结果如表1 所示，可以看出改进卡尔曼滤波对数据的处理效果更好，平均定位误差降低了8.28%，使得后面指纹库插值的数据更加可靠。

表1 滤波前后定位误差Tab.1 Positioning accuracy before and after filtering

5.1.2 CDV筛选算法的阈值分析与选取

采用CDV 筛选算法对检测到的每个AP 进行差分方差计算。图7 表示各个AP 计算得到的差分方差累积分布情况，可看出约70%的AP 的差分方差都在［0，100］dBm2范围内，表明大部分AP 包含的位置信息量较少，对位置信息的变动不敏感。图8表示在线AP个数越多，AP提供的位置信息量越多，定位误差越小，但当AP个数继续增大时，AP提供的位置信息已足够进行准确定位，定位误差基本保持不变。图9表示的是差分方差阈值与平均定位误差的关系，其中每个点(x，y)代表的是当选择x为差分方差阈值时，将差分方差小于x的AP 筛除，利用保留下来的AP 重新建立指纹数据库，再使用AWKNN算法进行匹配定位，定位误差为y。

由图9 可知定位误差在［0，100］dBm2范围内变化最小且精度较高，进一步分析得表2，可知未进行筛选时，离线AP个数为455，平均定位误差为1.34 m，当差分方差阈值为小于50 dBm2时，平均定位误差基本保持不变，当差分方差阈值继续增大时，平均定位误差开始逐渐的增大，由此可见要选择的最佳差分方差阈值位于［50，60］dBm2范围内。由表3可知当差分方差阈值为57 dBm2时，定位算法误差达到临界值，且此时离线AP 个数为182，相比于未筛选时指纹数据库大小减小了60%，此时定位精度与未筛选时基本保持一致，表明CDV 筛选策略可在保证定位精度不变的前提下，大大缩小指纹数据库的规模。

表3 ［50，60］dBm2内的筛选定位结果Tab.3 Screening location results in［50，60］dBm2

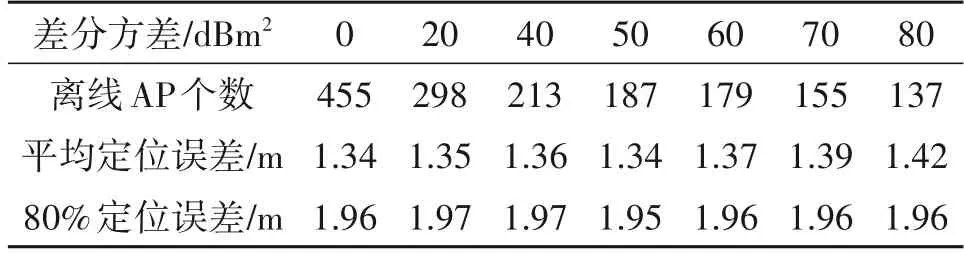
表2 不同差分方差阈值的筛选定位结果Tab.2 Screening and positioning results of different difference variance thresholds

为了验证CDV 算法的筛选性能，将CDV 与MCD 筛选算法进行对比，实验场景与上文一致，采用AWKNN进行定位，其结果如表4所示。由表4可得，当两种AP 筛选算法都选取自身最佳阈值时，其平均定位误差均与未筛选时1.34 m 基本保持一致，而MCD 算法筛选后保留了195 个离线AP，CDV算法筛选后保留了182 个离线AP，相比于MCD 算法，CDV 算法的离线AP 个数减小了7.14%。因此本文提出的CDV 算法的筛选性能要优于MCD算法。

表4 MCD算法与CDV算法的筛选性能对比Tab.4 Comparison of screening performance between MCD algorithm and CDV algorithm

5.1.3 插值误差分析

将SVR-Kriging 与克里金插值、线性插值（Lin⁃ear Interpolation，Linear）、IDW 算法进行对比。在同样的试验场景下进行间隔1.2 m 的插值，并求出插值点与实际测量信号强度的误差，其结果如表5 所示。可以看出SVR-Kriging 相比克里金插值进行了有效的改进，插值精度提高了9.34%，较线性插值和IDW也表现出了较好的优势。

表5 不同插值方法的平均插值误差Tab.5 Interpolation errors of different interpolation methods

5.2 定位误差分析

本文中三维定位采取先判断楼层，再确定位置的策略，具体流程如图10 所示，实验证明通过此方法对于楼层判定的准确率为100%。

基于本文改进的卡尔曼滤波算法、CDV 筛选策略和SVR-Kriging来构建指纹数据库，将构建的数据库通过AWKNN 匹配算法进行定位实验，并与其他插值算法进行对比。二维区域的结果如表6 所示，SVR-Kriging 较克里金插值平均定位误差降低了13.68%，同样也低于Linear 和IDW，不同插值方法累计误差分布如图11所示。三维区域的结果如表7所示，误差累计分布如图12 所示，实验结果表明SVR-Kriging 插值较克里金插值平均定位误差降低了15.60%，比线性插值平均定位误差降低了22.03%，比IDW平均定位误差降低了10.68%。

表6 不同插值方法的平均定位误差（二维）Tab.6 Positioning errors of different interpolation methods（2D）

表7 不同插值方法的平均定位误差（三维）Tab.7 Positioning errors of different interpolation methods（3D）

6 结论

本文研究了一种稀疏参考点下的室内定位方法，提出了高精度指纹数据库的构建算法。第一步对卡尔曼滤波加入了缺失点的判定，抑制了Wi-Fi的噪声和信号缺失的干扰，较常规卡尔曼滤波得到的定位误差减小了8.28%。第二步设计了基于CDV 的AP 筛选算法，在保证定位精度的前提下指纹数据库规模减少了60%，降低了定位成本。第三步提出了SVR-Kriging进行数据库的重构，减少了指纹采集工作量，比克里金插值精度提高了9.34%。本文通过多组实验在二维和三维区域分别得到了1.01 m 和0.92 m 的平均定位误差，算法定位精度高，在室内定位中有较大的应用前景。